Розв'язування задач на теорему Фалеса
Тема. Розв'язування задач на теорему Фалеса
Мета: закріпити знання учнів про зміст узагальненої теореми Фалеса, а також про означення та властивості подібних трикутників; удосконалювати вміння застосовувати вивчені твердження під час розв'язування задач.
Тип уроку: комбінований.
Наочність та обладнання: конспекти 6, 11.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Розв'язання домашніх задач і додаткової задачі учні перевіряють за записами на дошці, виконаними заздалегідь кількома учнями. Під час перевірки додаткової задачі звертаємо увагу на такі контрольні моменти:
- дане в умові число є не що інше, як коефіцієнт подібності трикутників, отже, дорівнює відношенню шуканих сторін;
- оскільки коефіцієнт подібності менший від 1, то сторона першого трикутника менша, ніж відповідна сторона другого трикутника.
Тому розв'язання задачі зручно виконувати, склавши рівняння: ![]()
(де х — довжина більшої сторони в метрах).
III. Формулювання мети і завдань уроку
Мета уроку безпосередньо випливає з його теми. Оскільки на попередніх уроках було вивчено достатньо великий об'єм навчального матеріалу, учні мають закріпити знання цього матеріалу, сформувати сталі вміння виконувати запис рівностей для відповідних геометричних об'єктів на основі вивчених тверджень, а також розв'язувати задачі із використанням вивченої теорії.
IV. Актуалізація опорних знань
Виконання усних вправ
-
Якщо AB · CD = MH · PK, то
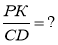
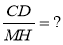
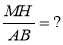
-
 ΔМНР ~ ΔKBD . Що звідси випливає?
ΔМНР ~ ΔKBD . Що звідси випливає?
- Чи можна стверджувати, що довільні два рівносторонні трикутники подібні?
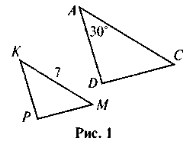
- ΔРKM ~ ΔDAC, k = 2 (рис. 1). Що можна знайти?
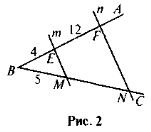
- Паралельні прямі т і п перетинають сторони кута ABC (рис. 2). Знайдіть довжину відрізка MN, якщо BE = 4, EF = 12, ВМ = 5.
-
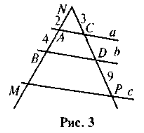
 Паралельні прямі a, b і с перетинають сторони кута MNP (рис. 3).
Паралельні прямі a, b і с перетинають сторони кута MNP (рис. 3).
Знайдіть довжини відрізків CD і MB, якщо AN = 2, NC = 3, DP = 9, АВ = 4.
V. Засвоєння вмінь та навичок
Виконання усних вправ
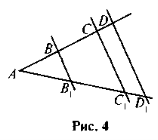
- ВВ1 || CС1 || DD1, АВ = 5, ВС = 4, CD = 1 (рис. 4). Знайдіть: a) AB1 : В1С1; б) AB1 : AD1; в) AD1 : В1C1.
- Чи подібні трикутники, якщо їхні сторони дорівнюють:
а) 1 м, 1,5м, 2 м і 10 м, 15 м, 20 м;
б) 2 см, 3 см, 4 см і 6 дм, 4 дм, 8 дм?
-
У трикутнику ABC провели всі середні лінії. Скільки подібних три
кутників утворилось? - У трикутнику ABC провели А1С1 || АС. Знайдіть АС, якщо А1С1 = 2, ВА1 = 3 , СА1 = 6 .
Виконання письмових вправ
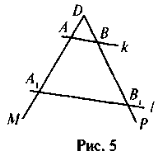
- Паралельні прямі k і l перетинають сторони кута MDP (рис. 5). Знайдіть довжину відрізка АА1, якщо DA = 8 , ВВ1 = 9 , АА1 = 2DB.
-
 ΔАВС ~ ΔА1В1С1. Знайдіть:
ΔАВС ~ ΔА1В1С1. Знайдіть:
а) АС, якщо А1С1 = 2, В1С1 = 3ВС;
б) РАВС, якщо АС = 3, А1С1 = 1 , ![]() = 7 .
= 7 .
-
Доведіть від супротивного, що тупокутний
і рівносторонній трикутники не можуть бути
подібними.
VI. Самостійна робота
Для перевірки якості засвоєння знань та вмінь учнів проводиться комплексна самостійна робота, яка складається як з теоретичних питань, так і з практичних завдань.
Варіант 1
- Чи можуть бути подібними прямокутний і рівнобедрений трикутники?
- Відомо, що ΔАВС ~ ΔMNK , РΔАВС : PΔMNK = 2 : 3. Знайдіть відношення NK : ВС.
- На рисунку ΔАВС ~ ΔА1В1С1, РАВС = 15 . Знайдіть х, у і z.
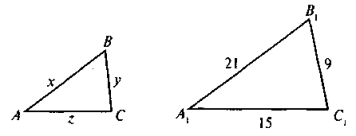
-
Відомо, що ΔАВС ~ ΔXYZ . Знайдіть кут В, якщо
 X = 123°,
X = 123°,  C = 18°.
C = 18°.
- Сторони трикутника дорівнюють 18 см, 27 см, 36 см. Знайдіть периметр трикутника, подібного до даного, якщо його найменша сторона дорівнює 36 см.
Варіант 2
- Чи можуть бути подібними рівнобедрений і тупокутний трикутники?
- Відомо, що ΔАВС ~ ΔMNK, МК : АС = 2 : 7. Знайдіть відношення РАВС : РMNK.
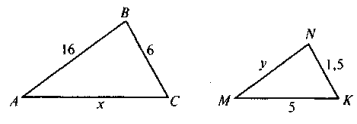
- На рисунку ΔАВС ~ ΔMNK . Знайдіть х і у.
-
Відомо, що ΔАВС ~ ΔXYZ . Знайдіть кут X , якщо
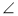 B = 72°,
B = 72°, 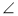 Z = 93°.
Z = 93°.
- Сторони трикутника дорівнюють 48 см, 24 см, 56 см. Знайдіть периметр трикутника, подібного до доданого, якщо його найбільша сторона дорівнює 7 см.
Після виконання завдань самостійної роботи учні здають розв'язання вчителю і відбувається перевірка розв'язання (за записами на дошці або із використанням ТЗН чи роздавального матеріалу).
VII. Домашнє завдання
Повторити зміст теоретичних тверджень; означення рівних трикутників, а також означення та властивості трапеції. Розв'язати задачі.
- Сторони трикутника дорівнюють 16 см, 12 см і 10 см. Знайдіть периметр трикутника, подібного даному, якщо його найбільша сторона дорівнює 8 см.
- Доведіть за означенням, що будь-які два рівносторонні трикутники подібні.
- Доведіть, що трикутник з вершинами в серединах сторін даного трикутника подібний даному. Чому дорівнює коефіцієнт подібності?
- Через вершину трикутника проведено пряму, яка ділить даний трикутник на два рівні трикутники. Визначте вид даного трикутника. Чи може така пряма розділити трикутник на два нерівні, але подібні, трикутники? Висловіть припущення.


про публікацію авторської розробки
Додати розробку
