Розв’язування задач на відсотки (навчально-методичний посібник)

Бібліотека Математика 9 клас Методичні рекомендації
Про матеріал
Предмет дослідження: розв’язування задач на відсотки з переважним використанням основних правил дії з десятковими і звичайними дробами. Мета роботи - скласти практичний посібник з розв'язування задач на відсотки для школярів. Завдання дослідження: 1) Вивчити історичний і теоретичний матеріал з певного питання. 2) Систематизувати задачі на відсотки за типами. 3) Скласти практичні рекомендації щодо вирішення задач на відсотки. 4) Виявити практичне застосування таких задач. Практична значимість роботи. Даний посібник з розв'язування задач на відсотки буде цікавий не тільки школярам 5-6 класу, яким цікава математика. Тут знайдуть багато корисного і випускники шкіл, і абітурієнти при підготовці до випускних і вступних іспитів Вчителі шкіл, гімназій можуть використати для роботи на уроках та заняттях гуртка і факультативу.
Перегляд файлу

Отчетный период для расчета условных процентов в 2013 году Доманівський навчально-виховний комплекс

«Доманівська загальноосвітня школа І-ІІІ ст. №1 –

Центр дитячої та юнацької творчості»

 

 

 

 

Розв’язування задач на відсотки

(навчально-методичний посібник)

 

 

Морозенко Ірина Олексіївна

вчитель математики та фізики

Доманівського НВК

«Доманівська ЗОШ І-ІІІ ст.№1-

Центр дитячої та юнацької творчості»

Доманівського району

 

 

 

 

 

 

 

 

2019

 

 

ЗМІСТ

Вступ………………………………………………………………….

Розділ 1. Основні типи задач з теми «Відсотки»  

  1.           Розв’язування  задач на застосування основних понять про відсотки………………………………………………. 

Розділ 2. Застосування відсотків

     2.1. Розв’язування  задач на поняття "процентний вміст", "концентрація", "%-й розчин"

2.1.1. Процентний вміст. Процентний розчин……………

2.1.2. Концентрація ………………………………………..

      2.1.3. Розв’язування  задач з використанням поняття  коефіцієнта збільшення ……………………………. 

2.1.4. Розв’язування задач на сушіння…………………….

2.1.5. Розв’язування задач на переливання ………………

 2.2. 3астосування відсотків в фізиці, хімії, біології ……….

2.2.1. Відсотки в фізиці……………………………………. 

2.2.2. Відсотки в хімії  …………………………………….

2.3. Застосування відсоткових розрахунків при розв’язуванні економічних задач ………………………. 

Розділ 3. Способи розв’язування задач на відсотки

3.1. Метод відсоткових символів ……………………………. 

3.2. Задачі на складання рівнянь  …………………………….

3.3. Задачі на знаходження наближеного значення числа ….

Розділ 4. Різні задачі на відсотки…………………………………

4.1 Тестові завдання на відсотки ……………………………. 

4.2. Вибрані задачі варіантів зовнішнього незалежного оцінювання………………………………………………… 

Висновок……………………………………………………………… 

Бібліографія …………………………………………………………

Додатки  ……………………………………………………………..

4

 

 

7

 

 

 

11

11

 

13

14

14

15

15

17

 

17

 

22

27

28

31

31

 

32

33

34

36

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вступ

Слово відсоток від латинського слова pro centum, що буквально означає «за сотню» або «зі ста». Ідея вираження частин цілого постійно в одних і тих же частинах, викликана практичними міркуваннями, народилася ще в давнину у вавілонян. Ряд завдань клинописних табличок присвячених обчисленню відсотків, однак вавилонські лихварі вважали не «зі ста», а «з шістдесяти».

Відсотки були особливо поширені в Стародавньому Римі. Римляни називали відсотками гроші, які платив боржник позикодавцю за кожну сотню. Від римлян відсотки перейшли до інших народів Європи. Довгий час під відсотками розумілися виключно прибуток або збиток на кожні сто рублів. Вони застосовувалися тільки в торгових і грошових угодах. Потім область їх застосування розширилася, відсотки зустрічаються в господарських і фінансових розрахунках, статистикою, науці і техніці.

Нині відсоток - це окремий вид десяткових дробів, сота частка цілого (що приймається за одиницю). Знак % походить, як вважають, від італійського слова cento (сто), яке у відсоткових розрахунках часто писалося скорочено cto. Звідси шляхом подальшого спрощення в скоропису буква t перетворилася на похилу риску (/), виник сучасний символ для позначення відсотка. У шкільному підручнику «Математика, 5»авторів М.Я. Віленкіна та ін. дана ще одна цікава версія виникнення знака %.[2] Там, зокрема, говориться, що цей знак стався в результаті безглуздої помилки, вчиненої укладачем. У 1685 р. в Парижі була опублікована книга-посібник комерційної арифметики, де помилково укладач замість cto надрукував %

Сучасне життя робить задачі на відсотки актуальними, так як сфера практичного застосування процентних розрахунків розширюється. Питання інфляції, підвищення цін, зростання вартості акцій, зниження купівельної спроможності стосуються кожної людини в нашому суспільстві. Планування сімейного бюджету, вигідного вкладення грошей у банки, неможливі без уміння проводити нескладні відсоткові обчислення.

Самі відсотки не дають економічного розвитку, але їх знання допомагає в розвитку практичних здібностей, а також вміння вирішувати економічні завдання. Обдумане вивчення відсотків може сприяти розвитку таких навичок               як               економічність,               розважливість.
У варіантах вступних іспитів зустрічаються задачі на відсотки, і ці завдання часто викликають труднощі у школярів. Причина в тому, що перше знайомство з відсотками починається у п’ятому класі, поширюється – у шостому класі, потім поступово продовжується і дев’ятому класі вивчається тема «Складні відсотки», яка доповнює понятійний апарат з даної теми, а в старших класах до цієї теми зовсім не повертаються. А в шкільному курсі є цикл предметів природничого спрямування, де відсоткові розрахунки необхідно знати для розв’язування задач з хімії, фізики, біології. Дана робота написана вчителями з метою допомоги учням та об’єднання теоретичних знань з теми «Відсотки» та практичного їх використання для розв’язування задач з математики, фізики, хімії, біології.

Тому, вивчення найбільш вживаних типів задач на відсотки, вважається               актуальним.
Об'єктом дослідження є вивчення різних типів задач з теми «Відсотки».

Вивчаючи цю тему за збірниками для вступників до вузів[9,15,20,22], приходимо до висновку, що багато завдань автори збірників пропонують вирішувати з використанням спеціальних формул, яких у шкільних підручниках 5-6 класів, коли і вивчаються ці теми, немає.

Предмет дослідження: розв’язування  задач на відсотки з переважним використанням основних правил дії з десятковими і звичайними дробами.

Мета роботи - скласти практичний посібник з розв'язування задач на відсотки для школярів.

Завдання дослідження:

1) Вивчити історичний і теоретичний матеріал з певного питання.

2) Систематизувати задачі на відсотки за типами.

3) Скласти практичні рекомендації щодо вирішення задач на відсотки.

 4) Виявити практичне застосування таких задач.

Практична значимість роботи. Даний посібник з розв'язування задач на відсотки буде цікавий не тільки школярам 5-6 класу, яким цікава математика. Тут знайдуть багато корисного і випускники шкіл, і абітурієнти при підготовці до випускних і вступних іспитів Вчителі шкіл, гімназій  можуть використати для роботи на уроках та заняттях гуртка і факультативу.
Бажаємо успіхів у навчанні!

 

 

 

 

 

 

 

 

 

 

Розділ 1. Основні типи задач з теми «Відсотки»[1,3,4,10]

…спробуємо на хвилину уявити собі,

 що ми всі втратили елементарні арифметичні знання.

 Адже це приведе до справжньої суспільної катастрофи,

бо арифметичний розрахунок супроводить нас на кожному кроці.
Б. В. Гнєденко

У даному розділі  наводяться приклади задач, які розв’язуються із застосуванням означення, що таке один відсоток, як виразити дріб у відсотках і правилами знаходження частини (дробу) від числа та числа за значенням його частини (дробу), тобто це ті теми і задачі, які розглядаються в               школі. Звертаємо увагу, що існують і інші способи розв'язання найпростіших задач на відсотки, наприклад, складають пропорції на кожному кроці, але в цьому випадку рішення стає на кілька кроків довше. Ми ж бачимо своє завдання в знаходженні більш швидких способів вирішення таких завдань, у зв'язку з тим, що в даний час рідкісний тест з математики для абітурієнтів, не обходиться без завдань, у яких не згадувалися б відсотки.

  1.             Розвязування  задач на застосування основних понять про відсотки

Сота частина метра - це сантиметр, сота частина карбованця - копійка, сота частина центнера - кілограм. Люди давно помітила, що соті частини величин зручні в тактичній діяльності. Тому для них було придумано спеціальну назву - відсоток. Значить одна копійка - один відсоток від одного карбованця, а один сантиметр - один відсоток від одного метра.
Один відсоток - це одна сота частина числа. Математичними знаками один відсоток записується так: 1%.[21]

Означення одного відсотка можна записати рівністю:  1  %  =  0,01 · а 

5%=0,05,     23%=0,23,     130%=1,3  і т. д

Як знайти 1% від числа? 1% це одна сота частина, треба число поділити на 100. Ділення на 100 можна замінити множенням на 0,01. Тому, щоб знайти 1% від цього числа, потрібно помножити його на 0,01.

А якщо потрібно знайти 5% від числа, то множимо дане число на 0,05 і т.д.

Приклад 1. Знайти: 25% от 120.

Розв’язання:
1)  25%=0,25;
2) 120 . 0,25 = 30.

Відповідь : 30.

Правило 1. Щоб знайти дане число відсотків від числа, треба записати відсоток десятковим дробом, а потім число помножити на цей десятковий дріб

Приклад 2. Токар виточував за годину 40 деталей. Застосувавши різець з більш міцної сталі, він став виточувати на 10 деталей у годину більше. На скільки відсотків підвищилася продуктивність праці токаря?
Розв’язання : Щоб розв’язати  цю задачу, треба дізнатися, скільки відсотків становлять 10 деталей від 40. Для цього знайдемо спочатку, яку частину становить 10 від числа 40. Ми знаємо, що потрібно розділити 10 на 40. Вийде 0,25. А тепер запишемо у відсотках - 25%. Отримуємо відповідь: продуктивність праці токаря підвищилася на 25%.(Додаток А)

 Правило 2. Щоб знайти, скільки відсотків одне число становить від іншого, потрібно розділити перше число на друге і отриманий дріб записати у вигляді відсотків.

Приклад 3. При плановому завданні 60 автомобілів в день завод випустив 66 автомобілів. На скільки відсотків завод виконав план?

Розв’язання: 66:60- таку частину складають виготовлені автомобілі від кількості автомобілів за планом. Запишемо у відсотках 110%

Відповідь: 110%

Приклад 4. 1. На скільки процентів 10 більше 6?    

    2.  На  скільки  процентів  6  менше  10?
 Розв’язання:
1.  ((10  -6).100%)/6=662/3%
2. ((10 - 6).100%)/10 = 40%

Відповідь : 66 2/3 %,  40 %.

Приклад 5.  Бронза є сплавом олова і міді. Скільки відсотків сплаву становить мідь в шматку бронзи, що складається з 6 кг олова і 34 кг міді?

Розв’язання:  1)   6+ 34 =40 (кг)  -  маса всього сплаву.

2)  34:40·100   = 85%  -   сплаву складає мідь.

Відповідь . 85%.

Приклад 6. Що станеться з ціною товару, якщо спочатку її підвищити на 25%, а               потім               знизити               на               25%?
Розв’язання : Нехай ціна товару х грн, тоді після підвищення товар коштує 125% попередньої ціни, тобто 1,25х;, а після зниження на 25% , його вартість становить 75% або 0, 75 від підвищеної ціни, тобто 0,75 *1,25х= 0,9375х, тоді ціна товару знизилася на 6, 25 %, тому х - 0,9375х = 0,0625х ; 0,0625х/х . 100% = 6,25%.

Відповідь: початкова ціна товару знизилася на 6,25%.(додаток В)

Правило 3. Щоб знайти відсоткове відношення двох чисел а і в, треба відношення цих чисел помножити на 100%, тобто обчислити (а/в)·100%.

Приклад  7 .  Знайти число, якщо 15% його дорівнюють 30.
Розв’язання:
1) 15% = 0,15;
2) 30 : 0,15 = 200.
або:   х - дане число;    0,15.х = 300;     х = 200.
Відповідь : 200.

Приклад  8. З бавовни-сирцю виходить 24% волокна. Скільки треба взяти бавовни-сирцю, щоб отримати 480кг волокна.?
Розв’язання . Запишемо 24% десятковим дробом 0,24 і отримаємо задачу про знаходження числа за відомою йому частиною (дробом). 480 : 0,24= 2000 кг = 2 т
Відповідь: 2 т

Приклад 9. Скільки кг білих грибів треба зібрати для отримання 1 кг сушених, якщо при обробці свіжих грибів залишається 50% їх маси, а при сушінні залишається 10% маси оброблених грибів?
Розв’язання :1кг сушених грибів - це 10% або 0, 01 частина оброблених, тобто 1 кг : 0,1=10 кг оброблених грибів, що становить 50% або 0,5 зібраних грибів, тобто 10 кг : 0,05=20 кг
Відповідь: 20 кг

Приклад  10. Свіжі гриби містили по масі 90% води, а сухі 12%. Скільки вийде сухих грибів з 22 кг свіжих?
Розв’язання:
1) 22 . 0,1 = 2,2 (кг) - грибів по масі в свіжих грибах; (0,1 це 10% сухої речовини)
2) 2,2 : 0,88 = 2,5 (кг) - сухих грибів, одержуваних з свіжих (кількість сухої речовини не змінилася, але змінився її процентний вміст у грибах і тепер 2,2 кг це 88% або 0,88 сухих грибів).
Відповідь: 2,5 кг.(Додаток В)

Правило 4. Щоб знайти число за даними його відсотками, треба виразити відсотки у вигляді дробу, а потім значення відсотків розділити на цей дріб.

 

Розділ 2. Застосування відсотків

2.1. Розвязування  задач на поняття "процентний вміст", "концентрація", "%-й розчин"[11]

2.1.1. Процентний вміст. Процентний розчин.

Приклад 1. Скільки кг солі на 10 кг солоної води, якщо процентний вміст солі 15%.
Розв’язання . 10 . 0,15 = 1,5 (кг) солі.
Відповідь: 1,5 кг

Процентний вміст речовини в розчині (наприклад, 15%), іноді називають %-м розчином, наприклад, 15%-й розчин солі.

Приклад 2. Сплав містить 10 кг олова і 15 кг цинку. Який процентний вміст олова і цинку в сплаві? (Додаток Г)
Розв’язання : Процентний вміст речовини в сплаві - це частина, яку складає маса даної речовини від маси всього сплаву.
1) 10 + 15 = 25 (кг) - сплав;
2) 10/25 . 100% = 40% - відсотковий вміст олова в сплаві;
3) 15/25 . 100% = 60% - відсотковий вміст цинку в сплаві;
Відповідь: 40%, 60%.

2.1.2. Концентрація.

Якщо концентрація речовини в з'єднанні по масі становить р%, то це означає, що маса цієї речовини складає н% від маси всього з'єднання.

Приклад 3. Концентрація срібла у сплаві 300 г становить 87%. Це означає, що чистого срібла в сплаві 261 р.
Розв’язання: 300 . 0,87 = 261 (р).
У цьому прикладі концентрація речовини виражена у відсотках.(Додаток Д)

Відношення об’єму  чистого компонента в розчині до всього об'єму суміші називається об'ємною концентрацією цієї компоненти.
Сума концентрацій всіх компонент, що складають суміш, дорівнює 1.
Якщо відомо процентний вміст речовини, то його концентрація знаходиться за формулою: К=р/100% к - концентрація речовини; р - процентний вміст речовини (у відсотках).

Приклад  4 . Є 2 сплава, в одному з яких міститься 40%, а в іншому 20% срібла. Скільки кг другого сплаву потрібно додати до 20 кг першого, щоб після сплавки разом одержати сплав, що містить 32% срібла?
Розв’язання : Нехай до 20 кг першого сплаву потрібно додати х кг другого сплаву. Тоді отримаємо (20 + х) кг нового сплаву. В 20 кг першого сплаву міститься 0,4 . 20 = 8 (кг) срібла, в х кг другого сплаву міститься 0,2х кг срібла, а в (20+х) кг нового сплаву міститься 0,32 . (20+х) кг срібла. Складемо рівняння:
8 + 0,2х = 0,32 . (20 +х); х = 13 1/3.
Відповідь: 13 1/3 кг другого сплаву потрібно додати до 20 кг першого, щоб одержати сплав, що містить 32% срібла. (додаток Г)

Приклад  5. До 15 л 10%-ного розчину солі додали 5%-ний розчин солі і отримали 8%-ний розчин. Яку кількість літрів 5%-ного розчину додали?
Розв’язання:Нехай додали х л 5%-ного розчину солі. Тоді нового розчину стало (15 + х) л, в якому міститися 0,8 · (15 + х) л солі. У 15 л 10%-ного розчину міститься 15 · 0,1 = 1,5 (л) солі, у х л 5%-ного розчину міститься 0,05х (л) солі.
Складемо рівняння.
1,5 + 0,05х = 0,08 · (15 + х);
х = 10.
Відповідь: додали 10 л 5%-ного розчину.

2.1.3. Розв’язування  задач з використанням поняття коефіцієнта збільшення[6,13,14]

Щоб збільшити додатне число а на р процентів, слід помножити числа а на коефіцієнт збільшення до=(1+0,01р).
Щоб зменшити додатне число а на р процентів, слід помножити числа а на коефіцієнт зменшення до= (1-0,01р).

Приклад  6. Внесок, вкладений в ощадбанк два роки тому, досяг суми, що дорівнює 13125грн. Яким був початковий внесок при 25% річних?
Розв’язання. Якщо а (гривень) - розмір початкового внеску, то в кінці першого року вклад складе 1,25а, а наприкінці другого року розмір вкладу становитиме 1,25 ·1,25а. Розв’язуючи рівняння 1,25·1,25а=13125, знаходимо а=8400.
Відповідь: 8400 грн.

Приклад  7. У лютому ціна на нафту збільшилася на 12% у порівнянні з січневою. У березні ціна нафти впала на 25%. На скільки відсотків березнева ціна змінилася в порівнянні з січневою?
Розв’язання. Якщо х - січнева ціна нафти, то лютнева ціна нафти дорівнює                           (1 +0,01·12)х = 1,12х.

Щоб обчислити березневу ціну на нафту, слід помножити лютневу ціну 1,12х на

(1-0,01·25)=0,75, тобто у=0,75· 1,12х=0,84х , березнева ціна відрізняється від січневої на (0,84х)/100 -100=84-100= -16(%), тобто ціна впала на 16 %
Відповідь: ціна впала на 16%.

 Правило 5. Щоб знайти, на скільки % одне число у відрізняється від іншого числа а , слід вирахувати, скільки % у становить від а і від отриманого числа відняти а.

2.1.4. Розв’язування задач на сушіння[16] (додаток Е)

Приклад 8.Свіжі гриби містять 90% води, а сухі 12% . Скільки сухих грибів вийде з 22 кг

Розв’язання:

Склад речовини

I

II

С

22

х

К

0,1

0,88

М

2,2

2,2

х = = 2,5.

Відповідь: 2,5.

 

2.1.5. Розв’язування задач на переливання[1,16,19] (додаток Є)

Приклад 9. У посудині 729 літрів чистої кислоти. Відлили а літрів і долили водою. Так зробили 6 разів, отримали 64 літрів чистої кислоти. Знайти а.

Розв’язання:

Ак = Ан (1 - )n

= (1 - ),             

а = 243.

Відповідь: 243.

Приклад 10. У посудині 20 літрів спирту. Частину відлили і долили водою. Потім ще раз відлили і долили водою. Після цього в посудині виявилося спирту втричі менше, ніж води. Скільки спирту відлили вперше?

Розв’язання:

Ан =20,      Ак =5.

= (1 - ),   

1 - = 0,5.      а = 10.

Відповідь: 10л.

 

2.2. 3астосування відсотків в фізиці, хімії, біології  [28]

Практика постійно пропонує різноманітні задачі, в тому числі й задачі на відсотки. Для ефективного розв’язуваня даних задач потрібно не тільки знати закони, але й уміти їх аналізувати, необхідно продумувати залежності, що існують між величинами.

2.2.1. Відсотки в фізиці
Ми продемонструємо вам застосування відсоткових розрахунків при розв’язуванні практичних задач з фізики.

Робота і енергія  (Додаток Ж)

Приклад 11. За допомогою підйомника, до складу якого входить рухомий блок масою 5 кг, піднімають вантаж масою 95 кг. Обчисліть ККД підйомника. Тертям знехтувати.

Дано:                                                       Розв’язання

m(в)=95 кг                           Згідно із означенням ККД

m(б)= 5 кг                                                 

ККД - ?                                     ККД =  Ак / Ап ·100%

Корисна робота – це робота з піднімання вантажу масою 95 кг на необхідну висоту:

                                          Ак = m(в)gh.

Виконана робота – це робота з піднімання вантажу разом із блоком:

                                        А(в) = (m(в) + m(б))gh

Остаточно отримаємо:

ККД =   ( m(в)gh )/ ((m(в)  +  m(б))gh)·100% =m(в)/( m(в)  + m(б))· 100%.

Обчислення :           

                             ККД = 95 кг /(95кг  + 5 кг)·100% = 95%.

Відповідь: ККД = 95%.

 

Теплові машини (Додаток З)

Приклад 12. Скільки літрів бензину витратив автомобіль потужністю 100 кВт на шляху у 240 км, який він пройшов зі швидкістю 80 км/год? ККД двигуна становить 35%.

Дано:                                                           Розв’язання

N=100кВт = 100000Вт      Автомобіль витратив певну кількість бензину,                                

l = 240 км = 240000 м        який згоряючи в циліндрах двигуна, виділив   

v = 80 км/год = 22,2 м/с          кількість  теплоти

ККД = 35%                                   Q = qm = qVρ.

ρ = 710 кг/м3                       За час руху двигун виконав роботу

q = 46000000 Дж/кг                          A = Nt = N:(1/ V).    

       V - ?                                     Згідно з визначенням ККД         

                                               ККД = А /Q·100%

 Звідси отримуємо             V = Nl /( qρvККД)·100%.

  Обчислення:

V=(100000·240000)/ (35·46000000·710·22,2)·100 =0,0945 м3

Відповідь: V = 0,0945 м3.

 

2.2.2. Відсотки в хімії

Приклад 13.Обчислити відсотковий склад по масі хімічних елементів у сульфатній кислоті.

                                            Розв’язання

Обчислюємо відносну молярну масу сульфатної кислоти

          М(H SO ) = 2+32 + 64 = 98

Маса Нідрогену становить 2, Сульфуру – 32, Оксигену – 64.

%(Н) =  2/98·100% = 2%.

%(S) = 32/98·100% = 32,7%.           

% (О) = 100% - 2% - 32,7% = 60,3%.

Відповідь: %(Н) = 2%, %(S) = 32,7%, %(О) = 60,3%.

 

2.3. Застосування відсоткових розрахунків при розв’язуванні економічних задач [10,13,14]

     При подачі нової теми доцільно повторити і узагальнити теоретичний матеріал,  який застосовувується при  опрацюванні та закріпленні практичної частини даної теми.

     Блок ,,А’’. Теорія.

      Первинний процес повторення включає в себе відновлення в пам’яті задач і  формул на розрахунок відсотків. До найпростіших задач на відсотки відносяться: [24]

  1.                    Знаходження відсотка від даного числа.

(якщо число х становить п% від числа а, то х=) .

  1.                    Знаходження числа за його відсотком.

(якщо про число х відомо, що його п% дорівнює b, то х=b:).

  1.                    Відсоткове відношення двох чисел.

(відсоток, який число а0 становить від числа b0, знаходимо за формулою     %).  [3 ]

На наступному етапі подається формула простих відсотків [24]:

 Ап= А0(1+). І= А0рn, І= Ап-А0 - формули дають змогу обчислювати прибуток з капіталу, загальну суму (майбутню, завершену вартість) та основну суму (поточну вартість). А0 — капітал (основна сума, початкова вартість, поточна вартість, номінальна вартість) — кількість позичених або вкла­дених (інвестованих) грошей, р — відсоткова ставка — нарахування прибутку у вигляді відсотків від основної суми за один рік, Ап — загальна сума (основна сума плюс прибуток, майбутня вартість, завершена вартість) — сума, яка виникла на кінець обумовленого проміжку часу n, І – прибуток, ціна, яку треба сплатити за використання грошей.

Слід мати на увазі, що прості відсотки використо­вуються переважно у короткочасних фінансових опе­раціях.

Блок ,,В’’. Теорія.

Для обчислення складних відсотків вивчаємо формулу :

Ап =  А0 (1+)n [24],  де  р — відсоткова ставка за певний період, п — загальна кількість періодів нарахувань,  А0 — початковий капітал — кількість вкладених або позичених гро­шей, Ап  — нарощений капітал — сума, яка утвориться на кінець обумовленого проміжку часу. Період — це проміжок часу між двома послідовними нарахуваннями грошей. Нарахування складних відсотків можна здійсню­вати щомісяця (12 раз нарік), щоквартально (4 рази на рік), кожного півріччя (2 рази на рік) тощо. Їх називають відповідно, щомісячним, квартальним, піврічним. Проміжок часу між двома послідовними підрахунками вартості грошей називають конверсійним періодом.

Блок ,,С’’. Теорія.

Для опрацювання на гуртку доцільно ознайомити учнів з використанням формули, яка застосовується, якщо кожного разу відсотковий приріст різний -

 Ап = А0(1+)(1+)…(1+) .

Для закріплення теми задачі також згруповано у блоки.

Блок ,,А’’. Задачі для осмислення набутих знань з теми ,,Формула простих відсотків’’.

Хто такий емітент?[25]

Емітент – це будь-яка організація або державний орган, які випускають в обіг гроші та цінні папери.

Емітентом може бути юридична особа, органи виконавчої влади чи органи місцевого самоврядування, що несуть від свого імені зобов'язання перед власниками цінних паперів по здійсненню прав, закріплених цими цінними паперами.

Емітентом може виступати орган виконавчої влади, місцевого самоврядування або юридична особа, якій у встановленому порядку, на певних умовах надане право емісії (випуску в обіг) грошей, облігацій, акцій та інших цінних паперів і документів, включаючи кредитні, (пластикові) картки, дорожні чекі.Емітент несе від свого імені зобов'язання перед власниками грошей і цінних паперів по здійсненню прав, закріплених ними.

  Приклад 14.( Тема ,,Банк і банківська система’’. Завдання на розрахунок прибутку емітента.)  Емітент відкрив депозит у розмірі 2 000 грн. у банк під виплату 18% річних. Яку суму він одержить через 10 місяців.[10]

  Розв’язання. 1 спосіб. Відсоткова ставка р ==1,5% за місяць.

Ап=2 000(1+ )=2 300 (грн).

2 спосіб. За умовою р=18%, n=. Ап=2000(1+)=2 300 (грн).

Відповідь. Емітент одержав 2 300 гривень.

Приклад 15. (Тема ,,Кредитні відношення’’. Завдання на розрахунок кількості грошей кредиту.)  Клієнт сплатив банку 100 грн. відсотко­вих платежів за кредит, наданий на 10 місяців під 0,1% річних. Яку суму грошей отримав клієнт цього банку як кредит?

 Розв'язання. За умовою I =100 грн.,  р= 0,1,

n= 10 місяців =року = року.

Суму грошей обчислимо за формулою:

 А0 =, А0 = 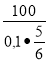   = 1 200(грн).

Відповідь. Клієнт отримав у банку кредит 1 200 грн. (Додаток М)

 Приклад 16. (Тема  ,,Інвестиція’’.  Завдання на розрахунок кількості грошей, необхідних для здійснення інвестиційної діяльності.)  Яка повинна бути сума початкового вкладу при відкритті депозиту за умови виплати 20 % річних, щоб одержати прибуток у 20 000 грн. через: а) 5 роки; б) 9 місяців. 

Розв'язання. За умовою Ап = 20 000 грн., р == 0,2 ,

а) n=5 років, А0===10 000 (грн).

б)  n==0,75 року, А0==17 391,30 (грн).

Відповідь: а) 10 000грн.; б) 17 391,30 грн.

 

Блок ,,В’’. Задачі на використання формули складних відсотків.[10,24]

Приклад 17. ( Тема ,,Банк і банківська система’’. Завдання на розрахунок прибутку емітента.)  У день народження сина його батьки відкрили депозит у сумі 1000 грн. у банку під виплату 18 % річних із щорічним нарахуванням складних відсотків. Яка сума грошей буде на цьому рахунку, коли сину виповниться 20 років?

Розв'язання. За умовою задачі А0 = 1000 грн., р = 18 % = 0,18, n = 20. Тому

Ап=1000(1+0,18)20=1000·27,393=27393(грн).

 Отже, на рахунку буде 27 393 грн.

Розв’язування запропонованих задач економічного характеру на відсоткові розрахунки ознайомлюють учнів з застосуванням формул відсоткових розрахунків у сфері фінансів та банківській справі, розкривають можливості математики у економічній теорії, сприяють розвитку та активізації математичного мислення, зацікавлюють учнів у вивченні даних предметів, озброюють їх знаннями щодо здійснення операцій з фінансовими інструментами, стимулюють самостійне опрацювання додаткових джерел та засобів Інтернет ресурсу. Завдяки цьому мотиваційна наповнюваність навчального процесу розширює спектр поповнення пізнавальної діяльності учня та сприяє оптимізаційному розвитку їх розумових та творчих здібностей. Таким чином основне завдання навчального процесу по формуванню креативної особистості учня досягається в основному за рахунок розвитку логічного мислення, яке повинно включати в себе уміння поетапного моделювання розв’язку задачі, тобто

  1.               Виявлення тематичної спрямованості задачі (розкриття сутності взаємозв’язку між економічною темою та вибором моделі розв’язку задачі).
  2.                    Визначення етапів розв’язання даної моделі.
  3.                    Вести пошук альтернативної ідеї розв’язування задачі

за допомогою засвоєних формул.

   4)  Створення раціональної схеми розв’язування запропонованого завдання з метою оптимізації обсягів отриманого прибутку.

     Задачі можна використати  для індивідуальної роботи, факультативних і гурткових занять.

 

Розділ 3. Способи розв’язування задач на відсотки

3.1. Метод відсоткових символів[8, 26]  

Метод розв’язування задач з використанням символьної рівності назвемо методом відсоткових символів.

Формула 1:     р%= = 0,01pa.  (1)

Наслідок:   р%=b ;   p a=b100.  (2)

У загальному виді:  р%=х ,  тобто  р а = х 100 ; х = р а : 100(відсоток від числа)

р% [х] = b, тобто  p x = 100 b,  звідки   х = ( число за його відсотком).

 х%[а] = b ,   або   х а = 100 b.  Звідси   х = (відсоткове відношення двох чисел).

 Як бачимо, всі три елементарні задачі на відсотки розв’язуються  подібно, фактично як одна.

Розв’язати   символічне рівняння легко, важкість полягає в його складанні, а саме в тому, щоб у символічні дужки попало саме те число          ( відоме чи невідоме), яке приймається за 100% і ніяке інше.

Для цього поняття «відсоток» повинно бути засвоєне учнями ґрунтовно, іншими словами, учень повинен твердо засвоїти, що саме в тій чи іншій задачі приймається за 100%.

Розмірковувати над тим, до яких з трьох типів задач потрібно звернутись немає потреби.

Можна підвести учнів до самостійного формулювання правил на підсумковому занятті гуртка, не ставлячи вимоги знати їх напам’ять.

Використовуючи відсоткові символи, пропонується виведення формул, тверджень, наслідків, які полегшують розв’язування багатьох складних задач.

Твердження 1:

р%[а] + q%[b] + c%[d] + .......+ t %[k] = u%[w] 

pa + qb + cd + ......tk = uw

Доводиться дане твердження на основі формули (1)

Приклад 1:

1.  50%[45] + 40% - 30% =   р%    

50 45 + 40 35 30 – 30 25 = р   55

2.  a%[5]  - b%[15]  = 10%[a-b]     a 5 – b 15 = 10(a-b)

 

Формула 2:

p%[a] + p%[b] + p%[c] +……. p%[h] = p%[a+b+c+….h] .

Доведення:    За  формулою (1) ліва частина:

p%[a] + p%[b] + p%[c] +……. p%[h] = +++ ...+ =

= p%[a+b+c+….h] .

Таким чином, ліва частина рівна правій частині.

Правильність формули доведена.

Приклад 2:

  1.      5%[9] - 5%[6] + 5%[3] =  5%[9-6+3] =5%[6].
  2.      a%[9] - a%[7] = a% [2].

Формула 3:

p%[a] + q%[a] + r%[a] +……. t%[a] = (p+q+r +…+t)%[a] .

Доведення:    За формулою (1) ліва частина рівності:

p%[a] + q%[a] + r%[a] +……. t%[a] =

+++…+= =

 (p+q+r +…+t )%[a].

Таким чином, ліва частина рівна правій частині.Правильність формули доведена.

1.Означення:

p%[ p%[ p%[… p%[a]… a] a] a]  = (p%)п[a] .

Приклад 3:

8%[8% [8% [10]]] =(8 %)3[10]

Формула 4:

(p%)п[a]  = ()п а

Довести дану формулу можна методом математичної індукції.

Для п = 1 формула очевидна. Припускаємо правильність її для п = к.  Легко доводиться, що вона буде правильна і для   п = к+1 .

Наслідок:

(р%)0[a]  = а    або а = (p%)0[a] .

  Доведення: за формулою  (р%)0[a]  =   ()0 а  = а

Приклад 4:

(5%)0[25]  = 25;   х = (с%)0[х]  .

Застереження:

(p%)п[a]  ≠  (pп)%[a] 

 

Приклад 5:

(100%)2[25]  ≠  1002%[25] 

2.  Означення:               p%[a]  = pа%[1]  .

Приклад 6:

10%[50]  = 50 = 10  1 = 10 50%[1]  .

 

Формула 5:    (p%)п[a]  = а (p%)п[1]  .

Доведення:   За формулою  (1):    (p%)п[a]  = ()п а .

а (p%)п[1]  =  а ()п 1 = ()п а  .

Таким чином, ліва частина рівна правій. Формула доведена.

 

Приклад 7:

(3%)5[13]  = 13 (3 %)5 [1]  ;

(4%)3[а-1]  = (а-1) (4%)3[ 1]  .

Формула 3:

(p%)п[кa]  = к (p%)п[а]  .

Доведення:   За формулою  1 :   (p%)п[кa]  = ()п ка .

к ( p%)п[а]  = к ()п а = ()п ка.

Таким чином, ліва частина рівна правій. Формула доведена.

Приклад 8:

(105%)2[15]  = 5 (105%)3[3]  ;

(b%)4[a(x+1)]  = a (b%)4[ x+1]  .

 

Формула 4:     (p%)п[1]  = (p%[1]  ) n.

Доведення :

За формулою  1 :   (p%)п[1]  = ()п 1 = ()п ;

(p%[1] ) n = ()п = ()п .

  Отже, ліва частина рівна правій. Формула доведена.

Застереження:

(p%[a])п  ≠  ()п а       при a ≠ 1; 0 ;  n ≠ 1.

Доведення:

За формулою 1 :   ()п а= (p%)п[a]

За формулою 1  :      ( р%)n = () n  = (p%[a])п  .

Застереження доведене.

Використання відсоткових символів досить ефективне, особливо при розв’язуванні задач на суміші та сплави

Задача. У лабораторії є суміш, загальна маса якої на 3,3 кг більша від маси титану, що міститься у ній. Якщо добавити до неї 2 кг суміші з 25 % вмісту титану, одержимо суміш, у якій 20 % ти­тану. Визначити початкову масу суміші і відсо­ток титану в ній.

Розв'язання

І спосіб ( традиційний)

Нехай m кг — початкова маса суміші, х% — вміст у ній титану.

Тоді  0,01 тх кг — маса титану в суміші.

У 2 кг нової суміші маса титану дорівнює 2 0,25 = 0,5 (кг).

Загальна маса титану при змішуванні сумі­шей становитиме

(0,01 тх + 0,5) кг, а загальна  маса змішаних сумішей (m+ 2) кг.

Складаємо систему рівнянь:

  m – 0,01mх = 3,3;

  100 =20 .  Домноживши перше рівняння на 100, отримали:

100m –mx = 330;

mx + 50=20m +40. Розв’язавши систему, отримали: m = 4; х = 17.5.

ІІ спосіб: ( метод відсоткових символів)

Нехай маса титану в суміші  - х кг, тоді маса титану –( х+3,3)кг. Відсоток титану в суміші позначимо через у. За умовою задачі:

у %[х+3,3]  +25%[2]  = 20%[х+5,3].  Крім того,  за умовою:

у%[х+3,3]  =х. Отже,   х+0,252 = 0,2 (х+5,3);

5х+2,5 = х+5,3;

х=0,7;     х+3,3 = 4;  За умовою:   у(х+3,3) = 100х; у4 = 1000,7;

у = 70:4 = 17,5.

Відповідь: 4 кг і 17,5%.    (Додаток Й)

 

3.2. Задачі на складання рівнянь [6, 12, 18]

Приклад 9. Під використання хімічних засобів захисту рослин було вщведено на 480га менше, ніж біологічних. Після того як було оброблено 25% хімічними i 80% біологічними засобами, площа, ще не оброблена біозасобами, виявилася на 300га меншою, ніж площа, не оброблена хімічними засобами. Яку плошу було вiдвeдeнo під хімічні i яку під біологічні засоби захисту рослин?

Розв’язання:

 

хімічні

біологічні

Biдведено

Х га

X + 480 га

Оброблено

25% - 0,25x га

80% - 0,8(х + 480) га

Залишилося

х - 0,25.x

(х + 480) - 0,8(х + 480)

                                                    300 га

х - 0,25х- (х + 480) - 0,8(х + 480) = 300, 0.75x – х - + 480 + 384 = 300,

 0,55x = 396,

х = 720.

хімічні - 720 га, біологічні - 1200 га. (Додаток К)

 

3.3. Задачі на знаходження наближеного значення числа

Екологічні спостереження часто супроводжуються вимірюванням кількісних характеристик екосистем. 3 ціею метою у польових умовах застосовують різноманітні  прилади, чутливість та точність вимірювань яких коливасться в широкому діапазоні. Інформативність вимірювань, можна значно покращити, провівши математичну обробку кількісних показників. Корисними можуть стати в даному випадку нерівності. Потреба нерівностей виникає при оцінці точності наближених обчислень. Відхилення результату від точного значения величини характеризують похибкою наближення-це різниця між точним i наближеним значениям величини. Причини виникнення похибок різноманітні:

  • похибки, пов'язані з приладом, яким проводить вимірювання -інструментальні;
  • обумовлені методом вимірювання- теоретичні;
  • залежать від дослідника, який здійснює вимірювання - суб’єктивні.

Похибка наближення може бути з недостачею(додатна) i надлишком (від'ємна).

Проте важливіше знати не характер наближення, а те, на скільки близьке воно до точного значення - модуль похибки наближення.

Коли за наближене значения числа х беруть число a i відомо, що модуль похибки такого наближення не перевищус деякого числа h, тобто Ix-aI<h, тo кажуть, що число а є наближенням числах х  точнітю до h. Записують це так: х=a±h.

 

Приклад 10. Пропустивши крізь сепаратор молоко, в якому масова частка жиру становить 3,8%, одержують вершки з масовою часткою жиру 7,0% i молоко з пониженим вмістом жиру. Обчислити межі масової частки жиру в молоці після сепаратора, якщо маса молока більша за масу вершків, а загальна маса жиру в молоці менша, ніж у вершках.

Розв'язаиня:

Нехай через сепаратор пропустили 100кг молока. Тоді позначимо через:

 х кг - масу вершків;

y кг - масу знежиреного молока;

z кг - масову частку жиру в молоці, яке пройшло через сепаратор.

Тодi  х +y =100.      (1)

Так як сума мас жиру в молоці після переробки i в вершках залишилася такою як в 100 кг молока, то:

  y + 0,07 х = 100·0,038 .   (2)

За умовою задачi: х< y, zy < 007х.    (3)

Знайдемо y: y=100- х, підставимо значення (2),(3).
               х < 100- х,

     z (100- х) < 007 х,

   (100- х)+ 007 х =100·0,038.

Знаходимо розв’язки рівняння з кожної нерівності.

      х <50,

 0,07 х+ z х>100,

  0,07 хz+ z х+ 100z=3,8.

Звідси:

z >0.006.

   z <0,026

Отже 0,006 < z <0,026.

Приклад 11. Змішали 7г розчину А, в якому є ioн бapiю i Зг розчину Б, шо містить сульфат-іон; випало 1,59г осаду сульфату барію з масовими частками барію 58,9% i сульфат-іона 41,1%. Коли змішали 4г розчину A i 6г розчину Б, то маса осаду становила 1,09г. Обчислити масові частки відповідних іонів у вихідних розчинах, враховуючи, що один з них взять у недостачі.

Розв'язання:

Нехай х г - масова частка іона барію, у - масова частка сульфат-іона.

В 1,59г осаду є:

  1.           1,59-0,589=0,937 (г) - іона барію;
  2.                      1,59-0,411=0,653 (г) - сульфат-іона

Отже масові частки іона барію i сульфат-іона в кожному розчині  відповідно не менші за:

0,939/7=0,134,       0,653/3=0,218  отже   х≥0,134,  у≥ 0,218  .

Аналогічно  після другого змішування: х ≥0,160, у≥ 0,075.

Macoві частки ioнa барію i сульфат-іона не можуть бути більшими за 0,160 i 0,218. Отже при першому змішуванні в осаді було 0,937г ioнa барію, а в 7г: 7· 0,16= 1,12г, що дещо більше, але осаду випало менше, бо не вистачало сульфат-юна в розчині, тому у= 0,218 i не більше. Подібним ходом міркувань доводимо, що х = 0,160. Отже масова частка іона барію 16%, сульфат-іона 21,8%.   (Додаток Л)

 

Розділ 4. Різні задачі на відсотки
В даному розділі розглядається вибірка завдань з різних джерел, які охоплюють весь теоретичний матеріал, який викладався вище, пропонуємо свої рішення. Відзначимо, що запропонований спосіб вирішення не є єдиним.

4.1 Тестові завдання на відсотки [9, 17, 18, 27](Додаток Н)

Приклад 1.Товар коштував тисячу гривень. Продавець підняв ціну на 10%, а через місяць знизив її на 10%. скільки став коштувати товар?

Розв’язання. Нехай товар коштував 1000грн., після підвищення ціни на 10% він став коштувати 1,1·1000грн. Після зниження цієї ціни на 10%, він став коштувати 0,9·1,1·1000=990грн.

Відповідь. 990грн.

 Приклад 2.Зібрали 100 кг грибів. Виявилося, що їх вологість 99%. Коли гриби підсушили, вологість знизилася до 98%. Якою стала маса цих грибів після підсушування?

Розв’язання. Так як вологість грибів становить 99%, це означає, що на так звану «суху речовину» припадає 1% грибів, тобто 1 кг, після сушки вологість становить 98%, тобто на «суху речовину» припадає 2%, тобто 1кг це 0,02 підсушених грибів, 1 кг : 0,02=50 кг.

Відповідь. 50 кг.

4.2. Вибрані задачі варіантів зовнішнього незалежного оцінювання [9,17,20,](Додаток О)

Аналізуючи завдання на відсотки в ЗНО проягом останніх років, можна зробити висновок, що необхідно серйозно працювати над даною темою. Якщо в 2008-2010 роках завдання на відсоткові розрахунки були представлені в І частині тесту, то в 2013-2014 в ІІ-гій частині. Слід зазначити, що для вирішення всіх завдань, які пропонувалися, досить знання тих методів, які розглядаються в даній роботі.

  1. Товар подешевшав на 20%. На скільки відсотків більше можна купити товару за ту ж саму суму грошей? (2006)
  2. Маємо два водно-сольових розчини. Концентрація солі в першому розчині становить 0,25, а в другому - 0,4. На скільки більше треба взяти кілограмів одного розчину, ніж другого, щоб отримати розчин масою 50 кілограмів, концентрація солі в якому - 0,34.(2008)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Висновок

Даний практичний посібник дозволить розвинути та закріпити навички розв'язування задач з теми «Відсотки», може бути цікавим учням, що захоплюється математикою, а також корисним випускникам шкіл та абітурієнтам при підготовці до іспитів.

Дана робота  є об’єднання теоретичних знань з теми «Відсотки» та практичного їх використання для розв’язування задач з математики, фізики, хімії, біології для учнів.

Робота може бути використана як посібник для учнів 5-11класів та вчителів шкіл, гімназій для роботи на уроках та факультативних заняттях.

Творче використання вчителем матеріалів, що пропонується у даній роботі, підвищує ефективність навчального процесу, робить його продуктивнішим, продуманішим, результативнішим, насиченим активними формами роботи.

Матеріал роботи буде корисним і для тих , хто навчає і для тих, хто вчиться.

 

 

 

 

 

 

 

 

 

 

 

Бібліографія

  1.          Василь Кравчук, Марія Підручна, Алгебра 9клас.–Т.:Підручники і посібники, 2009. – 256 с.
  2.          Виленкин Н.Я. и др., Математика 5. -Т .:Мнемозина, 2003, - 337с.
  3.          Г.П. Бевз, В.Г. Бевз , Математика 5клас.- К.: Генеза, 2005.-298с.:іл..
  4.          Г.П. Бевз, В.Г. Бевз , Математика 6клас.- К.: Генеза, 2006.-304с.:іл..
  5.          І.Л.Володін, В.В.Володін, Основи інформатики 7клас.- Х.: Гімназія, 2009. -352с.
  6.          Карцан Л. П. Алгебра. Як розв’язувати задачі. – Х.:Країна мрій, 2009. – 64 с.
  7.            Капіносов Анатолій  та інщі,  Математика. Комплексна підготовка до зовнішнього незалежного оцінювання. За чинною програмою ЗНО.-  Т.:Підручники і посібники, 2013 р.
  8.          Коноваленко В. Г., Следзинський И.Ф. Математическая символика. Пособие для самообразования учителей. Под редакцией доктора педагогических наук профессора Тесленко И. Ф. – К.: Радянська школа, 1981. – 25 л.
  9.          Конет І. М.  Математика. Довідник+тести. Повний повторювальний курс, підготовка до зовнішнього незалежного оцінювання: навч. посіб.–Кам`янець-Подільський:Абетка, 2009.– 340 с.
  10.     Кошколда  І.В. 334 задачі з економіки з розв’язками. /В.П.Щербань. – Харків: Гімназія, 2008.
  11.     Кравчук В., Підручна М., Янченко Г., Алгебра 9 клас.  Т.: Видавництво: Підручники та посібники, 2007. - 256 с.
  12.     Лук’янова Світлана. Розв’язування текстових задач арифметичними способами: 5-6кл. – К.:Вид. дім. «Шкільний світ»:Вид. Л. Галіцина, 2006. – 128 с.
  13.     Лисенко В.І. Економічні задачі у загальноосвітній школі.

/Ю.І.Пономаренко. Газета ,,Математика’’, №21(225), червень 2003, ст.13-19.

  1.     Межейнікова Л.С. Математичні задачі  з фінансовим змістом в основній школі./ В.О.Швець. - Харків. Видавнича група ,,Основа’’, 2005. – ст.13.
  2.     О.Істер.  Повний курс підготовки до вступних іспитів. - Київ. Видавництво А.С.К., 2007. – ст.42-48.
  3.     Мерзляк А. Г. , Полонський В. Б., Якір М. С., Алгебра:Підручн.для 9 кл. з поглибл. Вивченням математики. – Х.: Гімназія, 2009. – 384 с.: іл.
  4.     Навчально-тренувальні матеріали для підготовки до ЗНО. «Математика», Деніщева Л.О., Гдазков Ю.А. та ін, К: Інтелект-Центр, 2008, 2009, 2010, 2011, 2012
  5.     О.І.Глобін, О.В. Єргіна, Збірник завдань для ДПА з математики 9клас. – К.:Центр навчально – методичної літератури, 2013. - 268с.
  6.     Потапов М.К., Олехник С.Н., Нестеренко Ю.В. ,Конкурсные задачи по математике-  М: Наука, 1992, с.330-332.
  7.     Сканаві М.І.Збірник задач з математика для вступників до ВНЗ Видавництво: Арій Київ , 608с
  8.     Тарасенкова Н.А., Богатирьова И.Н., Бочко О.П., Коломієць О.Н., Сердюк З.А, Математика 5 клас -В: Освіта, 2013, 361с
  9.     Учебно-тренировочные материалы для подготовки к ЕГЭ. Математика, Денищева Л.О., Гдазков Ю.А. и др., М: Интеллект- Центр, 2003.
  10.     http://pro-status.com.ua/citaty/5/326_5.php 
  11.     http://yukhym.com/uk/matematika/zadachi-na-skladni-vidsotki.html  
  12.     http://vidpo.net/hto-takij-emitent.html
  13.     gomgoi@ukr.net
  1. http://www.lvtest.org.ua/testy-zno-mynulykh-rokiv
  2.     http://kindlebook.ru/referat/ucheba/protcenty-v-algebre-khimii-fizike/
  3.     http://www.stat.lviv.ua/ 

Додаток А              

Тип задач  на знаходження відсотків від числа [3, 4, 16,18]
1.А. Площа земельної ділянки 84 га, 75% її вже зорали. Скільки гектарів ділянки землі залишилось зорати?
Розв’язання.
1) 84: 100 • 75 = 63 (га) – вже зорали;
2) 84 – 63 = 21 (га) – залишилось зорати.
Відповідь: 21га
2.А. Із свіжих яблук отримали 18% сушених. Скільки сушених яблук отримають із 250 кг свіжих ?
Розв’ язання.
250 : 100 • 18 = 45 ( кг) – отримали сушених яблук
Відповідь: 45кг
3.А. За три дні машина проїхала 300 км. За перший день вона пройшла 30% шляху, за другий день – 35% шляху, за третій день – залишок шляху. Скільки кілометрів пройшла машина за третій день?
Розв’язання.
1) 300 : 100 • 30 = 90 (км) – пройшла машина за перший день;
2) 300 : 100 • 35 = 105 (км) – пройшла машина за другий день;
3) 300 – ( 90 + 105) = 105 ( км) – пройшла машина за третій день.
Відповідь: 105 км
4.А.  Одне число дорівнює 120, друге складає 50 % від першого, третє – 25 % від другого. Знайти середнє арифметичне цих чисел.
Розв’язання.
1) 120 • = 60 – друге число;
2) 60 • = 15 – третє число;
3) ( 120 + 60 + 15 ) : 3 65 – середнє арифметичне цих чисел.
Відповідь : 65
5.А.  Периметр прямокутника 180 см. Знайти сторони прямокутника, якщо одна з них на 20% менше , ніж друга.
Розв’язання.
В С Нехай сторона АД прямокутника АВСД
дорівнює х см, тоді сторона АВ , яка
менше на 20 % від АД дорівнює 0,8 х см
А Д (х: 100 • 20 = 0,2 х; х – 0,2 х = 0,8 х).
Периметр прямокутника дорівнює Р = 2 ( а + в ), за умовою задачі – 180 см.
Складемо і розв’яжемо рівняння:
(х + 0,8 х) = 180
1,8 х = 180 : 2
1,8 х = 90
х = 90 : 1,8
х = 50
Тоді АД = ВС = 50 см, АВ = СД = 50 •0,8 = 40 см.
Відповідь : 50см, 40см.
6 .А. Перший тракторист зорав 40 % поля, а другий зорав 35 % поля. Чому дорівнює площа всього поля, якщо перший зорав на 4 га більше?
Розв’язання.
Нехай площа всього поля дорівнює х га. Тоді перший тракторист зорав

0,4 х га (х : 100 • 40 = 0,4 х), а другий – 0,35 х га, що на 4 га менше, ніж перший. Складемо і розв’яжемо рівняння:
0,4 х – 0,35 х = 4
0,05 х = 4
х = 4 : 0,05
х = 80
Тоді площа всього поля дорівнює 80 га, перший тракторист зорав 0,4• 80 = 32 га, а другий – 0,35 • 80 = 28 га.
Відповідь : 80 га
7.А. Різниця двох чисел дорівнює 72. Знайти ці числа, якщо 4,5 % від одного з них дорівнює 8,5 % другого.
Розв’язання.
Нехай перше число дорівнює х, тоді друге – (х – 72).                                      4,5 % від першого дорівнює х : 100 • 4,5 = 0,045 х,                                              а 8,5 % від другого - (х – 72) : 100 • 8,5 = 0,085(х – 72).

Отримані числа рівні між собою. Складемо і розв’яжемо рівняння:
0,045 х = 0,085(х - 72)
0,045 х = 0,085 х – 6,12
- 0,04 х = - 6,12
0,04 х = 6,12
х = 6,12 : 0,04
х = 153
Тоді перше число дорівнює 153, а друге число – 81.
Відповідь : 153 і 81.

Висновок:
Щоб знайти відсоток від числа, треба :
Дане число поділити на 100 % і помножити на k %, або
1) Відсоток перевести у дріб ( поділити на 100 )
2) Число помножити на цей дріб.

 

 

 

 

 

 

Додаток Б

Знаходження відсоткового відношення[9, 11,20,21]
Наприклад:
Скільки відсотків число 5 становить від числа 20 ?
Розв̒язання.
Спочатку дізнаємось, яку частину число 5 становить від числа 20, а саме:
5 : 20 =2,5 , тепер помножимо це відношення на 100 % і отримаємо 25%.
Відповідь : 25%
1.Б. У класі навчається 30 учнів, серед яких - 21 дівчинка. Скільки відсотків дівчат навчається в цьому класі ?
Розв̒язання. Кількість дівчат у класі становить
21:30• 100% = 70%
Відповідь : 70%
2.Б.  За два дні турист пройшов 50 км. За перший день він пройшов 30 км. Скільки відсотків шляху йому залишилось пройти ?
Розв̒язання.  Нехай весь шлях становить 100%
1) 300:500• 100% = 60% - пройшов турист за перший день;
2) 100% - 60% = 40% – залишилось пройти туристу.
Відповідь : 40%
3 .Б. За планом робочий повинен був виготовити 200 деталей, а він виготовив 220 деталей. На скільки відсотків він виконав план ? На скільки відсотків він перевиконав план ?
Розв̒язання . Нехай план становить 100%. Тоді робітник, який виготовив 220 деталей , виконав план на
220:200• 100% = 110%
Він перевиконав план на 110 – 100 = 10 (%).
Відповідь: 110%, 10%.
4.Б. В 450 г розчину міститься 27г солі. Знайти відсоток солі в цьому розчині.
Розв̒язання. Відсоток солі, яка міститься в розчині знайдемо так :
27:450• 100% = 6%
Відповідь : 6%
 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток В

Задачі, в яких необхідно знайти невідоме число за його відсотками[1, 17]
1 .В. За планом тракторист повинен був зорати поле. Він зорав 2 га, що становить 75 % поля. Чому дорівнює площа всього поля ?
Розв̒язання.
1) 2 : 75 • 100 = 2 ( га) – площа всього поля
Відповідь : 2 га
2.В. Комбайнер перевиконав завдання на 15% і зібрав зернові з площі 230 га. Скільки гектарів за планом йому треба було обробити ?
Розв̒язання.
1) Нехай 100 % - це план, тоді комбайнер виконав 100 + 15 = 115 ( % ) від плану.
2) 230 : 115 • 100 = 200 ( га) – треба було обробити за планом.
Відповідь : 200 га
3 .В. Із свіжих груш виходить 18 % сушених. Скільки було взяти свіжих, щоб отримати 45 кг сушених ?
Розв̒язання.
1) Нехай 100 % становить вага свіжих груш,
2) 45 : 18 • 100 = 250 ( кг) – свіжих груш треба взяти.
Відповідь : 250 кг
4.В. Велогонщик в перший день пройшов 35 % довжини всієї траси, в другий день – 37 % всієї траси, а в третій день – останні 140 км. Яка довжина всієї траси ?
Розв̒язання.
1) Нехай 100 % - довжина всієї траси,
2) 35 + 37 = 62 (% ) – пройшов велогонщик за два дні,
3) 100 – 62 = 28 ( % ) – пройшов велогонщик за третій день,
4) 140 : 28 • 100 = 500 ( км ) – довжина всієї траси.
Відповідь : 500 км
5 .В. В коробці були кольорові олівці. Спочатку з коробки взяли 50 % олівців, потім – 40 % залишку. Після цього в коробці залишилось 3 олівця. Скільки олівців було в коробці ?
Розв̒язання.
1) Нехай в коробці лежало 100 % кольорових олівців,
2) 100 – 50 %– олівців залишилось в коробці після того, як взяли 1 раз,
3) 40 % від 50 % = 50 : 100 •40 = 20 % - олівців взяли з коробки 2 раз,
4) 50 – 20 = 30 % – олівців залишилось в коробці після того, як взяли
2 раз ,
5) 30 % від х дорівнює 3 олівцям, (х - всього олівців у коробці), Складемо і розв’яжемо рівняння:
0,3 х = 3
х = 3 : 0,3
х = 10
Тоді, в коробці було 10 олівців.
Відповідь : 10 олівців
6.В .Бригада теслярів використала на ремонт будівлі 4,2 м³ дошок. При цьому вона зекономила 16 % виділених для ремонту дошок. Скільки кубічних метрів дошок було виділено для ремонту будівлі ?
Розв̒язання.
1) Нехай 100 % дошок треба виділити на ремонт будівлі,
2) 100 – 16 = 84 (%) – дошок пішло на ремонт будівлі,
3) 4,2 м³ складає 84 % , тоді 84 % від х дорівнює 4,2 м³,
Складемо і розв’яжемо рівняння:
0,84 х = 4,2
х = 4,2 : 0,84
х = 5
Тоді 5 м³ дошок було виділено на ремонт будівлі.
Відповідь : 5 м³
7 .В.Свіжі гриби містять 90 % води, а сушені – 12 % води. Скільки сушених грибів отримають із 20 кг свіжих ?
Розв̒язання. Свіжі та сушені гриби містять воду та суху речовину ( мікроелементи, клітковина, білки, жири, вуглеводи та інше). Нехай свіжих грибів взяли 100%, що становить 20 кг за умовою задачі. Тоді сухої речовини вони містять 100- 90 = 10 (%), або 20 : 100 •10 = 2 (кг). При висиханні свіжі гриби втрачають вологу, а зміст сухої речовини не змінюється. Отже нехай тепер 100% становить вага сушених грибів, із яких 12% - це вода, тоді 100 – 12 = 88 (%) це – суха речовина грибів.
Знайдемо вагу сушених грибів :
2 : 88 • 100 = 2 кг
Відповідь : 2 кг
Висновок:
Щоб знайти число за його відсотком, треба:
Дане число поділити на k% та помножити на 100%, або:
1) Відсоток перевести у дріб ( поділити на 100),
2) Дане число поділити на цей дріб.
 

 

 

 

 

 

 

 

Додаток Г

Сплави[19, 22]

1.Г. У двох сплавах мідь і цинк відносяться як 4: 1 і як 1: 3. Після переплавки 10 кг першого і 16 кг другого і декількох кг чистої міді, отримали сплав, в якому цинк і мідь відносяться як 3, : 2. Визначити вагу нового сплаву.

                                                                Розв’язання:

Склад речовини

I

II

III

IV

С

10

16

х

26 + х

К

1

М

8

4

х

0,6(26 + х)

12+х = 0,6х+15,6;

х = 9;      26+9=35.   

 Відповідь: 35кг.

 

2.Г. З двох сплавів перший містить 7 кг, другий 8 кг міді. Отримали новий сплав, що містить 18 % міді. Який % зміст міді в першому сплаві, якщо в другому на 20 % її більше?

Розв’язання:

Склад речовини

I

II

III

С

 К

х

у

0,18

М

7

8

15

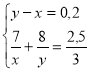
х = 12%

Відповідь: 12%.

3.Г. Є два сплави міді і цинку.  Першому міді в 2 рази більше, ніж цинку, а в другому - в 5 разів менше. У скільки разів більше потрібно узяти другого сплаву, чим першого, щоб отримати новий сплав, в якому цинку було б в 2 рази більше, ніж міді.

Розв’язання:

Склад речовини

I

II

III

мідь

2х

у

2(2х + у)

цинк

х

5у

х + 5у

(2х+у)·2 = х+5у,       

х = у,      

3х = 6у = 6х.

4.Г. Є два сплави з цинку, міді і олова. Перший містить 40% олова, другий 26 % міді. Відсотковий вміст цинку однаковий в обох сплавах. Сплавивши 150 кг першого і 250 кг другого, отримали новий сплав, в якому 30 % цинку. Скільки кг олова в новому сплаві?

Розв’язання:

                                             Цинк

Склад речовини

I

II

III

С

150

250

400

К

х

х

0,3

М

150х

250х

120

Олово

Склад речовини

I

II

III

С

150

250

400

К

0,4

0,44

 

М

60

110

170

400 х = 120 ,       

х = 0,3 = 30%.

Відповідь: 30%.

5. Г. Обчислити вагу сплаву срібла з міддю, знаючи, що, сплавивши його з 3 кг чистого срібла, отримають сплав, що містить 90 % срібла, а, сплавивши його з 2 кг сплаву, що містить 90 % срібла отримають сплав, що містить 84 % мідь.

 Розв’язання:

Ситуація перша

Склад речовини

I

II

III

С

х

3

х + 3

К

0,01у

1

0,9

М

0,01ху

3

0,9(х + 3)

Ситуація друга

Склад речовини

I

II

III

С

х

2

х + 2

К

0,01у

0,9

0,84

М

0,01ху

1,8

0,84(х + 2)

х = 3кг,    у = 80%..

Відповідь. 3кг. 80%.

 

6.Г. Є два зливки сплавів міді і олова. Перший - 3 кг містить 40 % міді, другий - 7 кг містить 30 % міді. Якої маси треба взяти кожен, щоб отримати 8 кг сплаву, що містить 32% мідь?

 Розв’язання:

Склад речовини

I

II

III

С

х

8 - х

8

К

0,4

0,3

0,32

М

0,4х

0,3(8 – х)

8·0,32

0,4х + 0,3(8 - х) = 8·0,32;           

х = 1,6кг.       

8 - 1,6 = 6,4кг.

Відповідь: 6,4кг.

7.Г. У сплав магнію і алюмінію, що містить 22 кг алюмінію, додали 15 кг магнію, після чого вміст магнію підвищилася на 33 %. Скільки важив сплав спочатку?

Розв’язання:

Склад речовини

I

II

С

х

15 + х

К

М

х - 22

х - 7

  – = 0,3.

х = 25.

Відповідь: 25.

8.Г. У 100 кг сплаву міді і цинку вміст міді складає 45% . Скільки  кг чистого цинку потрібно додати до сплаву, щоб кількість міді склала 20 % кількості цинку?

Розв’язання:

Склад речовини

I

II

С

100

100 + х

К

0,45

0,2

М

45

0,2(100 + х)

45 = 0,2(100 + х);             

х = 125кг.

Відповідь: 125кг.

9.Г. У першому сплаві мідь і цинк знаходяться у відношенні 1: 3, в другому 3: 5. Скільки кг першого сплаву потрібно сплавити з 15 кг другого, щоб в новому сплаві мідь і цинк знаходилися у відношенні 13: 27?

                                                                Розв’язання:

Склад речовини

I

II

III

С

х

15

15 + х

К

М

х

·15

(15 + х)·

х = 10

Відповідь: 10.

10.Г. Є два зливки міді. Відсотковий вміст міді в першому зливку на 40 % менше, ніж в другому. Після того, як обидва зливки сплавили, відсотковий вміст міді став 36 %. Знайти відсотковий вміст в першому зливку і в другому, якщо в першому було 6 кг міді, а в другому 12 кг

Розв’язання:

Склад речовини

I

II

III

С

К

х

0,4 + х

0,36

М

6

12

18

+ = ;

х = 20%;            20% + 40% = 60%.

Відповідь: 20%, 60%.

11.Г. Є два зливки золота і срібла. У першому їх відношення 1:2, в другому 2:3. Якщо сплавити 1/3 першого зливку і 5/6 другого, то в отриманому зливку буде стільки золота, скільки  в першому було срібла. Якщо ж 2/3 першого сплавити з 1/2 другого, то в зливку срібла, що вийшов, буде на  1кг більше, ніж золота в другому зливку. Скільки золота в кожному?

                                         Розв’язання:

Склад речовини

I

II

III

IV

С

х

у

К

 

М

х

у

()

 

() = х

 

 

 

 

 

 

 

 

 

 

 

Додаток Д

                                 Розчини[1, 9, 17, 20]

1. Д. У яких пропорціях треба змішати 50 % - ий розчин кислоти і 70 % - ий, щоб отримати 65 %-ий розчин кислоти?

                         Розв’язання:

Склад речовини

I

II

III

С

х

у

х + у

К

0,5

0,7

0,65

М

0,5х

0,7у

0,65(х + у)

0,15х = 0,05у,      

=

Відповідь: 1/3.

2.Д. Змішали 30 % - ий і 10 % - ий розчини соляної кислоти. Отримали 600 гр. 15 % - ого розчину. Скільки грамів узяли кожного розчину?

                          Розв’язання:

Склад речовини

I

II

III

С

х

у

600

К

0,3

0,1

0,15

М

0,3х

0,1у

90

х = 150  ,  у = 450 .

Відповідь: 150; 450.

3.Д.  Якщо змішати 8 кг і 2 кг сірчаної кислоти, то отримаємо 12% - ий розчин. При змішуванні двох однакових мас тих же розчинів, отримаємо 15% - ий розчин. Визначити концентрацію кожного.

                               Розв’язання:

Перша ситуація

Склад речовини

I

II

III

С

8

2

10

К

х

у

0,12

М

8х

2у

1,2

                                                            Друга ситуація

Склад речовини

I

II

III

С

z

z

2z

К

х

у

0,15

М

zх

zу

0.3z

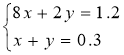
х = 0,1.    у = 0,2.

Відповідь: 10% . 20%.

4.Д.  До 120 гр. розчину, 80% солі,  додали 480 гр. розчину, 20% солі. Скільки відсотків солі вийшло в розчині?

Розв’язання:

Склад речовини

I

II

III

С

120

480

600

К

0,8

0,2

х

М

96

96

600х

600х = 192

х = 0,32 = 30%.

Відповідь: 30%.

5.Д. Змішали Р% - ий розчин кислоти з 10 %-м і отримали 600г. 15% -го розчину. Скільки гр. узяли кожного розчину?

Розв’язання:

Склад речовини

I

II

III

С

х

у

600

К

0,01Р

0,1

0,15

М

0,01Р х

0,1у

90

           

х = .     у = 600 - х.

Відповідь: , 600 – х.

6.Д.  Перший розчин містить 0,8 кг безводої сірчаної кислоти, а другий 0,6 кг. Відсотковий вміст сірчаної кислоти в першому розчині на 10 % більше, ніж в другому. Яка маса кожного розчину, якщо їх загальна маса 10 кг

                                                       Розв’язання:

Склад речовини

I

II

III

С

х

у

10

К

 

М

0,8

0,6

1,4

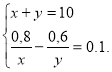
х = 4   у = 6.

Відповідь: 4. 6.

7. Д. Змішали 10% і 25% розчини солі отримали 3 кг 20% - го розчину. Яка кількість кожного розчину використана?

Розв’язання:

Склад речовини

I

II

III

С

х

у

3

К

0,1

0,25

0,2

М

0,1 х

0,25у

0,6

      

х = 1.  у = 2.

Відповідь: 1; 2.

8.Д.  Після змішування двох розчинів, один з яких містить 48 гр., а інший 20г. безводого йодистого калію, отримали 200г. нового розчину. Концентрація першого на 15% більше концентрації другого. Знайти концентрацію кожного.

Розв’язання:

Склад речовини

I

II

III

С

х

у

200

К

 

М

48

20

 

        

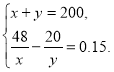
х = 120.      у = 80.

= 0,4 = 40%.      = 0,25 = 25%.

Відповідь: 40%, 25%.

9.Д. У посудину місткість 6 літ. налите 4 літ. 70% -го розчину сірчаної кислоти. У другу посудину такою ж місткістю налите 3 літ. 90% -го розчину сірчаної кислоти. Скільки літрів потрібно перелити з другої посудини в першу, щоб в ньому вийшов r %  розчину сірчаної кислоти.

Розв’язання:

Склад речовини

I

II

III

С

4

х

4 + х

К

0,7

0,9

0,01r

М

2.8

0,9 х

2.8 + 0.9 х.

х=

Відповідь: х =

10.Д.  Морська вода містить 5% солі. Скільки прісної води потрібно додати до 30 кг води, щоб концентрація солі стало 1,5%.

Розв’язання:

Склад речовини

I

II

III

С

30

х

30 + х

К

0,05

0

0,015

М

30·0,05

0

0,015(30 + х)

1,5 = (30 + х )·0,015.       

х = 70.

Відповідь: 70.

 

 

 

 

 

 

 

Додаток Е

 Розв’язування задач на сушіння

1.Е. Зібрали 140 кг. грибів, вологість яка складає 98% після підсушування їх вологість знизилася до 93%. Яка стала маса грибів.

Розв’язання:

Склад речовини

I

II

С

140

х

К

0,02

0,07

М

2,8

2,8

= 40.

Відповідь: 40.

2.Е.  17 кг свіжих грибів містять 90% води, сухі містять 15% води. Скільки вийде сухих грибів?

Розв’язання:

Склад речовини

I

II

С

17

х

К

0,1

0,85

М

1,7

1,7

= 2кг

Відповідь: 2кг.

 

 

 

 

Додаток Є

Переливання

1.Є. З бака, наповненого спиртом, вилили частину і долили водою. Знову вилили стільки ж і долили водою. Після цього в баку залишилося 49 літрів чистого спирту. Місткість бака 64 літри. Скільки літрів вилили вперше, і скільки в другій?

Розв’язання:

= (1 - ),    а =  8л.

= 1 - ,        а = 7л.

Відповідь: 8л., 7л.

2.Є.   З посудини, що містить 30л. спирту, відлили деяку кількість його і долили водою, потім відлили суміші на 2л. більше. У посудині залишилося 12л. чистого спирту Скільки літрів рідини відливали кожного разу.

Розв’язання:

= (1 - )(1 - ).

= (1 - )( - ).

15t - 29t + 8 = 0.       t = ,   t = .

Відповідь: а = 10л.

 

 

 

 

Додаток Ж

Робота і енергія[28]

Задачі для самостійного розв’язання.
1.Ж. Рівномірно піднімаючи вантаж вагою 100 Н за допомогою рухомого блоку, робітник прикладає силу 70 Н. Визначте ККД цього блоку.
2.Ж. За допомогою нерухомого блоку рівномірно підняли вантаж масою 45 кг на висоту 3 м. Який ККД блоку, якщо прикладена сила дорівнювала 500               Н               ?
3.Ж. Вантаж рівномірно піднімають за допомогою нерухомого блоку, прикладаючи силу 300 Н. Визначте масу вантажу, якщо ККД становить 70%.
4.Ж. За допомогою важеля рівномірно піднімають вантаж масою 245кг на висоту 6см, прикладаючи до більшого плеча силу 500 Н. При цьому точка прикладання сили опустилась на 0,3м. Визначте ККД важеля.
5.Ж. При рівномірному переміщені вантажу масою 15 кг за допомогою похилої площини динамометр показав силу 40 Н. Визначте ККД похилої площини , якщо її довжина 1,8 м , а висота 30 см.

 

 

 

 

 

 

 

Додаток З

 Теплові машини [28]

Задачі для самостійного розв’язання.
1.З. Тепловий двигун потужністю 50кВт щогодини витрачає 20 кг палива з питомою теплотою згоряння 36 МДж/кг. Який ККД цього двигуна ?
2.З. Знайдіть ККД двигуна трактора, який для виконання роботи в 1,89 •107 Дж використав 1,5 кг палива з питомою теплоємністю 4,2 •106Дж/кг.
3.З.  В паровій турбіні корисно витрачається ¼ частина всієї енергії, яка виділяється при згорянні палива. Знайдіть ККД парової машини.
4.З.  Використовуючи спиртовку, нагріли 300 г води від 18 до 68оС та спалили 7 г спирту. Знайдіть ККД спиртівки.

 

 

 

 

 

 

 

 

 

 

 

Додаток Й

 Методод відсоткових символів  [26]

1.Й.  У лабораторії є два ящики порошку. По­рошок в одному ящику містить 20 % заліза, у другому — 12 %. Скільки потрібно взяти по­рошку з кожного ящика, щоб отримати 3,2 кг порошку, що містить 15 % заліза?

Розв'язання

І спосіб:

Нехай з першого ящика потрібно взяти х кг порошку, а з другого — у кг.

Тоді х + у = 3,2.

0,2х кг — вміст заліза у порошку з першо­го ящика,

0,12у кг — вміст заліза у порошку з другого ящика.

У 3,2 кг порошку вміст заліза буде 3,20,15 = 0,48 (кг).

Маємо систему:

х+у = 3,2 ;

0,2х+0,12у = 0,48;

         х = 3,2-у,

        0,2 (3,2-у) +0,12у = 0,48;          у = 2; х=1,2.

ІІ спосіб: ( метод відсоткових символів)

Нехай з першого ящика потрібно взяти х кг порошку, а з другого — у кг.

Тоді  х + у = 3,2.

20%[х]+12% [3,2-х]=0,48;

0,2х +0,12(3,2-х) = 0,48;

0,08х = 0,096;

х =1,2 ; у = 2.

Відповідь: З першого ящика потрібно взяти 1,2кг, а з другого 2кг порошку.

2.Й.   Є шматок сплаву міді та олова, маса яко­го 12 кг. Він містить 45 % міді. Скільки чисто­го олова потрібно додати до цього шматка спла­ву, щоб новий сплав містив 40 % міді?

Розв'язання

І спосіб:

Визначимо, скільки міді міститься у 12 кг сплаву:

12 0,45 = 5,4 (кг).

Нехай потрібно додати х кг чистого олова,  тоді маса нового сплаву буде (12 +х) кг, у яко­му 5,4 кг міді, що становить 40%.

Маємо рівняння:

0,4(12 +х) = 5,4,

4,8 +0,4х = 5,4,

0,4х = 0,6,

х = 1,5.

ІІ спосіб:

Нехай потрібно додати х кг чистого олова,  тоді маса нового сплаву буде (12 +х) кг, у яко­му 5,4 кг міді, що становить 40%.

40%[12+х]=5,4;  0,4(12+х)=5,4;   0,4х = 0,6;

  х=1,5.

Відповідь. 1,5 кг.

3.Й. Є сплави двох сортів із вмістом нікелю 65 % і 40 %. Скільки слід взяти кожного з цих сплавів, щоб отримати 140 кг сплаву з вмістом нікелю 50 %?

Розв'язання  І спосіб:

Визначимо вміст нікелю у сплаві масою 140 кг, тобто знайдемо 50 % від 140 кг, це 70 кг.

Нехай маса сплаву із вмістом нікелю 65 % становить х кг, тоді 0,65х кг — вміст нікелю у ньому.

(140 -х) кг — маса сплаву із вмістом нікелю 40 %,тоді

0,4 (140 - х) кг — вміст нікелю в ньому.

Маса нікелю під час переплавлювання сплавів не змінилася, тому одержуємо рівнян­ня:

0,65х + (140-х)0,4 = 70;

0,65 + 56-0,4х = 70,

0,25х = 14;    х = 56 .

Отже, 56 кг — маса сплаву із вмістом ніке­лю 65 %.

140 - 56 = 84 кг — маса сплаву із вмістом нікелю 40 %.

ІІ спосіб:

Нехай маса сплаву із вмістом нікелю 65 % становить х кг, а (140 -х) кг — маса сплаву із вмістом нікелю 40 %. За умовою:

65%[х]+ 40%[140-х] = 50%[140];

0,65х+0,4(140-х)= 70;   0,65х+56- 0,4х = 70;     0,25х = 14;

х= 56.   140 - 56 = 84 кг — маса сплаву із вмістом нікелю 40 %.

Відповідь. 56 кг, 84 кг.

 

 

 

 

 

 

 

 

 

 

 

Додаток К 

Задачі на складання рівнянь

1.К. У голубів висиджування пташенят і їх годування до вильоту із гнізда продовжується 38 днів, при цьому період висиджування менший від періоду годування на 2 дні. Скільки продовжується період висиджування?

Розв’язування:

Годування

Х

Висиджування

Х-2

 

 

 

2х-2=38,

Х=18(днів)- годування;

Х-2=16(днів)- висиджування .

Відповідь: 16 днів.

2.К.  Визначити максимальну висоту польоту, на яку може підніматися під час міграції ластівка, якщо 2/25 висоти на 480м менше 0,2 цієї ж висоти?

 

 

 

 

 

 

 

 

Додаток Л 

Задачі на знаходження наближеного значення числа[7,19]

1.Л. Надій молока на фермі становить 450±20 кг, а загальна маса жиру в ньому -14 кг і вона не залежить відмаси надоїв. Обчислити межі масової частки жиру в молоці.

    2.Л.  Надземна частина рослини містить за масою 0,12% марганцю, а підземна 0,15%. Дослідник описав, шо в надземній частині рослини марганцю більше, ніж в підземній. Обчислити межі масової частки марганцю в цілій рослині.

   3.Л.  У надземній частині рослини масова частка води становить 88%, а в кореневій 70%. Обчислити можливу масову частку води в цілій рослині, якшо в невисушеному стані маса надземної частини більша, ніж кореневої, а після видалення води - навпаки.

   4.Л. Водоймише забруднено сполукою коричневого кольору, концентрашя якої прямо пропорційна до інтенсивності забруднення. Пробу забрудненної води порівнювали зі стандартами. Виявилось, що и концентрація була в межах 180-190 мг/л. Якшо досліджуваний розчин розвести водою в 5 разів, то концентрація сполуки буде в межах 35-40 мг/л. Обчислити концентрацію сполуки у воді водоймища та точність наближення результату.

   5.Л. Зола, що угворюється от згорання палива на теплових електростанціях, після часткової очистки від оксидов важких металiв викидається в атмосферу. Масова частка важких металів у золі 15%-17%. Пил затриманий очисними спорудами, містить за масою 20% оксидів важких металів, а в атмосферу викидаеться пил, що містить їх 12%. В яких межах знаходиться маса важких металів, що викидаються в атмосферу, після проходження через очисні споруди 100 тон золи?

 

Додаток М

Застосування відсоткових розрахунків при розв’язуванні економічних задач[10, 13, 14, 24]

1.М. ( Тема ,,Банк і банківська система’’. Завдання на розрахунок прибутку емітента.)   Під який відсоток емітент відкрив у банку депозит у розмірі 5000 гривень на 10 місяців, одержавши прибуток у сумі  6000 гривень.

Розв'язання.  За умовою Ап=6000 грн., А0=5 000 грн., n=10 місяців =

    =року= року . р===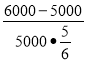0,24;    р=24%.

Відповідь. Емітенту потрібно відкрити депозит під 24%.

2.М. ( Тема ,,Банк і банківська система’’. Завдання на розрахунок прибутку емітента.)  На який термін потрібно відкрити депозит у розмірі 10 000 гривень під 15% річних, щоб отримати прибуток 16000 гривень.

 Розв'язання. За умовою Ап=16 000 грн., А0=10 000 грн., р=15%=0,15.

  n===4 (роки).

Відповідь. Потрібно відкрити депозит на 4 роки.

3.М. ( Тема ,,Банк і банківська система’’. Завдання на розрахунок прибутку банку.)   Банк відкриває депозити на умовах виплати 12 % річних і надає кредити на умовах оплати позичальникам під 18 % річних. Яким буде прибуток від      банківських операцій, якщо сума депозитів становить  20 млн. грн., а розмір кредиту 15 млн. грн. у рік?

Розв'язання.   18%=0,18;  12%=0,12.

 15 000 0000,18 – 20 000 0000,12=2 700 000-2 400 000=300 000 (грн).

 Відповідь. Банківський прибуток становить 300 000 гривень.

4.М. (грошовий обіг) Вирахувати співвідношення купівельної спроможності злотого і національної  грошової одиниці, якщо в споживчий кошик входять три продукти – А, Б, В у кількостях 10, 20, і 40, а ціни на них подані нижче:

Ціна в гривнях

20

12

5

Ціна в злотих

7,2

6,52

1,5

 

 

 

Купівельна спроможність грошової одиниці визначається співвідношенням сум у національних валютах для   придбання одиниці товару із запропонованого набору,  який входить до споживчого кошика в  кожній із країн. [16]

На споживчий кошик потрібно:

В гривнях 20 · 10+12 ·20+5 ·40=640.

В злотих: 7,2 ·10+6,52 ·20+1,5 ·40=262,4.

Відношення злотого до гривні:  за 1 гривню – 0,41 злотих.

Відношення гривні до злотого: за 1 злотий – 2,4 гривні.

    5.М. (Тема ,,Безробіття’’. Завдання на визначення безробіття.)  Населення Львівської області за даними Головного управління статистики у Львівській області станом на 1.01.2010 року становить 2549,6 тис. осіб. З них дітей до 16 років – 428 068,  людей, що знаходяться в психіатричних клініках і місцях ув’язнення, - 18 353, пенсіонерів – 563 237, безробітних –4 000. Визначити рівень безробіття в області. [29]

  Розв'язання. 2 549 600-(428 068+18 353+563 237)= 1 539 942 – робоча сила.

=0,26%   - рівень безробіття.

6.М.  ( Тема ,,Банк і банківська система’’.)  У банку ,,А’’ відкрито депозит на суму, яка становить 30% від суми депозиту у банку  ,,Б’’, а сума депозиту банку ,,Б’’ становить 55%  від суми депозиту вкладеного в банк ,,В’’, а в банку ,,В’’ відкрито депозит, на рахунку якого знаходиться сума ,  яка перевищує депозит у банку  ,,А’’ на 8350 гривень. На яку загальну суму відкрито депозити у трьох різних банках?

 Розв'язання. Нехай х гривень – сума депозиту у банку  ,,В’’. Тоді у банку  ,,Б’’     

 потрібно відкрити депозит на суму 0,55х гривень, а в банку  ,,А’’ –   

 (0,30,55х=0,165х)грн. За умовою х-0,165х=8350, 0,835х=8350, х=10 000(грн) -     

сума депозиту в банку ,,В’’. 0,5510 000=5 500(грн) - сума депозиту в банку ,,Б’’, 0,16510 000=1650(грн). Загальна сума, на яку відкрили депозити у трьох банках, становить 10 000 + 5 500 + 1 650=17 150(грн).

7.М. (Тема ,,Фінансові інструменти’’. Завдання на розрахунок дохідності.) Інвестор отримав облігацію номінальної вартості 3 200 грн зі строком погашення 3 роки та відсотковою ставкою 10% річних. Який прибуток отримає інвестор:

  1.                    Через три роки;
  2.                    Якщо через рік він продасть її за ринковою вартістю 3 750? [16]

Розв'язання. 1. 10%=0,1, 3 2000,1=320( грн) за 1 рік. За 3 роки – 960 (грн)

  1.                    3 750-3 200=550 (грн). 550+320=870 (грн) .

   8.М. (Тема ,,Фінансові інструменти’’. Завдання на розрахунок дохідності.) Ви маєте суму в 1000 гривень, яку хочете розмістити з метою отримання найбільшого доходу. Банк залучає кошти клієнтів на депозитні вклади під 8% річних; акціонерне товариство випустило цінні папери у вигляді 8 привілейованих акцій номінальною вартістю 250 гривень з виплатою дивідендів у розмірі 10% та 10 звичайних акцій номінальною вартістю 200 гривень. На виплату дивідендів акціонерним товариством відведено 800 гривень. Куди краще вкласти гроші:

  1.                    у банк;
  2.                    у привілейовані акції;
  3.                    у звичайній акції?

Розв'язання. 1) Якщо внести гроші на депозитний рахунок у банк, то через рік можна отримати 80 гривень у вигляді нарахованих та виплачених банком доходів.

2) Дивіденди на привілейовані акції складуть 810%=80% , тобто 80% від 800 складає 640 грн. Одна привілейована акція дає прибуток 80 грн. За 1000 грн. можна купити 4 акції по 250 грн. Прибуток буде 320 грн.

3) На виплати по звичайних акціях залишиться 800-640=160 (грн). А виплачені дивіденди на звичайну акцію становить 160:10=16(грн). Звичайних акцій можна купити 1000:200=5 і отримати прибуток 516=80(грн). Отже, найкраще придбати привілейовані акції акціонерного товариства.

 

Блок ,,В’’.      Задачі на використання формули складних відсотків.

9.М. ( Тема ,,Банк і банківська система’’. Завдання на визначення початкової суми депозиту.)   Яким повинен бути початковий вклад для відкриття депозиту у банку на 5 років при умові виплати 20 % річних за умови піврічного нараху­вання складних відсотків для того, щоб загальна сума на рахунку наприкінці п’ятого року склала 15 000 грн.?

Розв'язання. ,     P=5783 (грн).

Відповідь. У банк слід покласти 5783 грн.

10.М. ( Тема ,,Банк і банківська система’’. Завдання на визначення початкової суми депозиту.)  За 4 роки початкова сума вкладу, при виплаті 18 % річних при щоквартальному їх нарахуванні,  досягла 10000 грн. Знайти початкову суму вкладу.

Розв'язання. За умовою р = 18 % = 0,18 – річна ставка, n =4· 4=16, Ап=10 000 грн. р==0,045 – ставка відсотка за конверсійний період

А0 =4 944,69 (грн)

Відповідь. ≈4 944,69 грн.

Задача 11.М. ( Тема ,,Банк і банківська система’’. Завдання на розрахунок прибутку емітента.)   Три емітенти розмістили гроші в банку під 12% річних. Скільки через рік отримає кожний з них при умові, що сума вкладу кожного власника депозиту 1000 у.од., якщо перший прийде через рік, другий зніме й вкладе всю суму з нарахованими відсотками через півроку, а третій – раз у квартал?

Розв'язання.

  1.                    Перший, знявши через рік отриману суму, отримає 1120 у.од.
  2.                    Другий емітент, знявши гроші через півроку, отримає 1060 у.од.. Поклавши їх назад, через наступних півроку отримає 1123,6 у.од. або за формулою складних відсотків   1000 ·(1+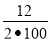)2=1123,6 (у. од.)
  3.   Третій емітент отримає:1000·(1+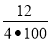)41125,51(у.од.).

12.М. ( Тема ,,Банк і банківська система’’. Завдання на розрахунок прибутку банку.)  Клієнт позичив у банку 50 000 грн. Банк надав кредит під 10 % при щоквартальному їх нарахуванні. Через 5 років боржник сплатив позику одноразовою сумою.

а) Знайти суму одноразової сплати.

б) Знайти прибуток банку.

Розв'язання. Оскільки р = 10 %, т = 4, то  р′ =0,025 .

Загальна кількість періодів п =5 ·4=20

Тоді Ап=50000 ·1,0252081930,8( грн), що становить суму одноразової сплати.   

Тоді прибуток банку дорівнює: 31930,8 грн.

13.М.  ( Тема ,,Банк і банківська система’’.)  На початку року є можливість внести в банк на рахунок 1640 гривень. Але в кінці року треба зняти з рахунку 882 гривні, а через рік знову –882 гривні. Під який відсоток потрібно внести гроші в банк, щоб вказані операції відбулися?[13]

Розв'язання. Нехай х% - щорічні відсоткові нарахування. Тоді на кінець року банк нарахував (0,01х1640) грн. і на рахунку в кінці року стало (1640+0,01х1640)грн., або (1640(1+0,01хНа початку другого вклад становив (1640(1+0,01хгрн. Відсоткові гроші, нараховані на цю суму становлять (0,01хгрн. А сума, яка була нарахована в кінці другого року               становить ((1640(1+0,01хгрн., що за умовою становить 882 гривні.

Отримаємо рівняння: (1640(1+0,01х)-882)(1+0.01х)=882. Введемо змінну у=1+0,01х. Тоді рівняння має вигляд: 1640у2+882у-882=0, звідси у1= - не задовольняє умови задачі,  у2=.  Тому 1+0,01х=, а х=5%

Блок ,,С’’.     Розрахунок рівня інфляції

Задача 14.М.     Вкладник поклав певну суму на рік під 20% у банк, в зв’язку з кризою через рік банк знизив відсоткову ставку до 15%. На який відсоток зросте початковий внесок емітента?

Розв'язання.  А0=х грн. Тоді х(1 +) (1 +)=1,38х, що становить % =138% від початкової суми, тобто початковий внесок зросте на 38%.

15. М. Петренко відкрив депозит на три роки. Договір передбачає наступну схему нарахування відсотків: за перший рік – 10%, а за кожний наступний ставка підвищується на 2%. Визначити на скільки відсотків зросте депозит Петренка за три роки?

    Розв'язання.  А0=х грн. Тоді х(1 +) (1 +) (1 +) 1,40 х, що становить % =140% від початкової суми, тобто початковий внесок зросте на 40%.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток Н   

Тестові завдання на відсотки[7, 9, 18]

  1.Н. Ціна вхідного квитка на стадіон була 1 гривню 80 копійок. Після зниження вхідної плати кількість глядачів збільшилася на 50% , а виручка зросла на 25% . Скільки став коштувати квиток після зниження?

Розв’язання . Нехай глядачів, до зниження ціни, на стадіон приходило А чол. і виручка становила 1,8А руб. Після зниження ціни, ціна 1,8·р, глядачів стало 1,5А, виручка становить 1,8·р·1,5·А руб. З іншого боку, виручка підвищилася на 25%, тобто становить 1,25·1,8А. Отримуємо 1,8р·1,5А=1,25·1,8А., звідки р=12,5/15, тоді квиток коштує 1,8·12,5/15=1,5грн.

Відповідь. 1грн 50 коп 

   2.Н. По дорозі йдуть два туриста. Перший з них робить кроки на 10% коротші і в той же час на 10% частіше, ніж другий. Хто з туристів йде швидше і чому?

Розв’язання . Нехай другий турист робить а кроків, кожен з яких дорівнює в, тоді ав це довжина пройденого шляху. А перший турист тоді пройшов1,1а·0,9в=0,99ав, що менше ав.

Відповідь. Другий турист йде швидше.

  3.Н .Ціну за товар зменшили на 10%, а потім ще на 10%. Коштує він дешевше, якщо відразу знизити ціну на 20%?

Розв’язання. Якщо товар коштував А крб, після двох знижень він став коштувати 0,9·0,9А=0,81А. А ціну товару відразу знизити на 20%, то він стане коштувати 0,8А , що дешевше.

Відповідь. Так.

 4.Н. Матроскін продає молоко через магазин і хоче отримувати за нього 2,5 грн за літр. Магазин утримує 20% вартості проданого товару. За якою ціною буде продаватися молоко в магазині?

Розв’язання .Нехай молоко продає магазин за А грн, тоді після утримання 20% вартості товару, Матроскіну залишається   

 0,8·А=2,5, звідки А=3,125 грн.

Відповідь. 3 грн 13 коп.

  5.Н . Один покупець купив 25% наявного шматка полотна, другий покупець 30% залишку, а третій - 40% нового залишку. Скільки (у відсотках) полотна залишилося непроданим?

Розв’язання. Нехай полотна було р . Перший купив 0,25р, залишилося (1-0,25)р полотна, другий покупець купив 0,3·0,75р=0,225р, залишилося 0,75р -0,225р=0,525р, третій купив 0,4·0,525р=0,21р, залишилося 0,525р-0,21р=0,315р, що становить 31,5% від р.

Відповідь. 31,5%

 6.Н .Бригада косарів у перший день скосила половину поля і ще 2 га, а у другий день-25% решти і останні 6 га. Знайти площу поля.

Розв’язання. 6 га становлять 75%  або 0,75=3/4 від решти після 1 дня роботи, тобто   6: 0,75=6 га  8+2=10 га - це половина поля, все поле 20 га

Відповідь. 20 га

 7.Н .Як зміниться у відсотках площа прямокутника, якщо його довжина збільшиться на 30%, а ширина зменшиться на 30%?

Розв’язання. АВ - площа даного прямокутника, 1,3А·0,7В=0,91АВ - площа нового прямокутника, що складає 91% початкового.

Відповідь. Зменшиться на 9%

 8.Н. У драматичному гуртку число хлопчиків становить 80% від числа дівчаток. Скільки відсотків становить число дівчаток в цьому гуртку від числа хлопчиків?

Розв’язання. Дівчаток А осіб, хлопчиків 0,8А, дівчатка складають від хлопчиків     А/(0,8А)= 1,25, тобто 125 % від числа хлопчиків

Відповідь. 125%

  9.Н. В басейн проведена труба. Внаслідок засмічення її приплив води зменшився на 60%. На скільки відсотків внаслідок цього збільшиться час, необхідний для заповнення басейну

Розв’язання. Нехай Х - обсяг води, який повинен надійти за час Т при припливі А в од часу, тобто Х=АТ. Так як приплив зменшився на 60%, тобто став складати 0,4А, тоді час став ТК. Отримаємо АТ=0,4АКТ, звідки К= 2,5, що становить 250% від часу, необхідного на заповнення басейну до засмічення, тобто час збільшилася на 150%

Відповідь. 150%

  10.Н . 5 літрів вершків з вмістом жиру 35% змішали з 4 літрами 20%-них вершків і до суміші додали 1 літр чистої води. Який жирності вийшла суміш?

Розв’язання. 0,35·5+0,2·4=р(5+4+1), звідки р=0,255, що становить 25,5%

Відповідь. 25,5%

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток О  

Вибрані задачі варіантів зовнішнього незалежного оцінювання [7, 17, 22, 27 ]

1.О. За переказ грошей клієнт повинен сплатити банку винагороду в розмірі 2% від суми пе-реказу. Скільки всього грошей (у гривнях) йому потрібно сплатити в касу банку, якщо сума переказу становить 30 000 грн? (2009)

2.О. Банк сплачує своїм вкладникам 8% річних. Скільки грошей треба покласти на рахунок,щоб через рік отримати 60 грн прибутку?(2010)

3.О. Журнал коштував 25 грн. через два місяці цей самий журнал став коштувати 21 грн. на скільки відсотків знизилася ціна товару?(2011)

4.О. Додатне число А більше додатного числа В у 3,8 раза. На скільки відсотків число А більше за число В?(2013)

5.О. Почпткова вартість сукні становила 144грн. унаслідок уцінення цієї сукні було зменшено на 60%. Обчиліть вартість сукні після уцінення. Скільки відсотків становить початкова вартість сукні від її вартості після уцінення?(2014)

6.О. Визначте вартість (у грн) спожитої за місяць користувачем пільгової категорії електроенергії(див. фрагмент квитанції). Урахуйте те, що тариф (вартість однієї кВт год) становить 0,28 грн. Надана цьому користувачеві пільга полягає в тому, що за 75 кВт год зі спожитих за місяць користувач сплачує на 25% менше від їхньої вартості за тарифом.

Відповідь: 26,95

 

 

 

 

 

1

 

Середня оцінка розробки
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Загальна:
5.0
Всього відгуків: 2
Оцінки та відгуки
  1. Кізюрін Віталій
    Кізюрін Віталій 21.01.2022 в 13:50
    Цікава робота.
    Загальна:
    5.0
    Структурованість
    5.0
    Оригінальність викладу
    5.0
    Відповідність темі
    5.0
  2. Коляда Коляда
    Коляда Коляда 26.07.2021 в 09:52
    Загальна:
    5.0
    Структурованість
    5.0
    Оригінальність викладу
    5.0
    Відповідність темі
    5.0
doc
Додав(-ла)
Морозенко Ірина Олексіївна
Пов’язані теми
Математика, 9 клас, Методичні рекомендації
Додано
26 лютого 2019
Переглядів
110403
Оцінка розробки
5.0 (2 відгука)
Безкоштовний сертифікат
про публікацію авторської розробки
Щоб отримати, додайте розробку

Додати розробку
Рекомендовані матеріали
pptx
2863 0
Математика і моя майбутня професія
doc
1030 0
Тренувальні тестові завдання для повторення матеріалу 5,6 класу під час підготовки учнів до ДПА
doc
1818 0
Множення іменованих чисел записаних у вигляді десяткових дробів.
pptx
2017 0
Презентація до уроку з математики на тему: "Множення іменованих чисел записаних у вигляді десяткових дробів."
Схожі матеріали
docx
19417 5
Головоломки з математики для учнів 6-9 класів
doc
1397 0
Конспект уроку-подорожі з математики для 9 класу на тему "Розв'язування вправ на всі дії з десятковими дробами"
zip
2314 4.3
Позакласний захід з математики для учнів 7-9 класів: інтелектуальний клуб "Клуб мудрої сови"
ppt
2390 5
Презентація "У кого бджоли - у того й мед" (заняття математичного гуртка для учнів 8-9 класів)
docx
5762 0
Підсумкові контрольні роботи, математика 9 клас
Завантажити
Зберегти на потім