Розв'язування задач на знаходження площі чотирикутників

Обчислення площі чотирикутників

Застосування нових формул

Задача 1. Знайти площу прямокутної трапеції, описаної навколо кола, якщо її основи дорівнюють 10см і 18см.

  В                С

           Нехай у трапецію АВСD вписано коло,                                                                                      

  А             Е        D

ВС=10см, АD=18см. Знайдемо площу трапеції АВСD.

        І спосіб:

Нехай АВСD – дана прямокутна трапеція, ВС||АD. Проведемо з вершини кута С висоту СЕ. СЕ=АВ. Тоді ЕD=АD-ВС.

СЕD – прямокутний, СЕD=90⁰. За теоремою Піфагора з СЕD

ЕD²= СD²-СЕ² ; ЕD²=(СD-СЕ)(СD+СЕ); (АD-ВС)²=(СD-СЕ)(СD+СЕ); звідси . Оскільки в трапецію можна вписати коло, то суми протилежних сторін рівні: ВС+АD= АВ+СD.

Тоді (см),  АВ+СD=18+10=28(см).

Маємо систему: 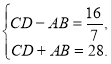  Звідси 2СD=; СD= см.

АВ= 28- СD, АВ= 28-=см.

Площа трапеції , . S=(см²).

ІІ спосіб:

Нехай АВСD – дана прямокутна трапеція, ВС||АD. Оскільки в трапецію можна вписати коло, то площа трапеції, дорівнює добутку її основ: .

10·18=180(см²).

Відповідь: 180см².

Як бачимо, другий спосіб має переваги над першим. Завдяки новим формулам  можна розв’язувати задачі в два рядки.

Задача 2. Діагоналі рівнобічної трапеції взаємно перпендикулярні. Знайдіть площу цієї трапеції, якщо її висота дорівнює 5см.(№31 [8]).

                В           С               Нехай АВСD - рівнобічна трапеція, АВ=СD, 

                                               АС ВD, висота h=5см. Знайдемо  площу  АВСD.                                                               

 

 

          А                       D

Оскільки в рівнобічній трапеції діагоналі перпендикулярні, то .

Тоді =25(см²).

Відповідь: 25см².

 

Задача 3. Знайти площу рівнобічної трапеції, якщо її основи дорівнюють 5см і 11см, а периметр 28см (№806 [1]).

   В              С            Нехай АВСD - рівнобічна трапеція, АВ=СD, ВС=5см,                            

                                   АD=11см, Р=28см. Знайдемо площу АВСD.

 

     А      К          Р       D

І спосіб:

У трапеції АВСD проведемо з вершин тупих кутів В і С висоти ВК і СР. Оскільки ВКАD, СРАD, то чотирикутник КВСР – прямокутник. За властивістю прямокутника ВС=КР, ВК=СР. АКВ і DРС – прямокутні і рівні за гіпотенузою і катетом: АВ=СD – за умовою, ВК=СР. З рівності трикутників випливає рівність сторін: АК=РD.

Тому АК=(АD-КР):2=(АD-ВС):2.     АК=(11-5):2=3(см).

Периметр трапеції Р=АВ+ВС+СD+АD=2АВ+ ВС+ АD;  звідси

2АВ=Р-( ВС+ АD),   АВ=( Р-( ВС+ АD)):2,   АВ=(28-(5+11)):2=6(см).

З прямокутного трикутника АКВ за теоремою Піфагора АВ²= АК²+ВК²;

ВК²= АВ²- АК²;  ВК²= 36-9=27;  ВК=(см).

Площа трапеції обчислюється за формулою:  , тому S=(ВС+АD)·ВК.

S=(5+11) ·=(см²).

Відповідь: см².

ІІ спосіб:

           Периметр трапеції Р=АВ+ВС+СD+АD=2АВ+ ВС+ АD,  то

2АВ=Р-( ВС+ АD),  АВ=( Р-( ВС+ АD)):2  і  АВ=(28-(5+11)):2=6(см).

Півпериметр , (см). Оскільки трапеція рівнобічна, то її можна вписати в коло. Тоді її площу обчислимо за формулою:. (см²).

Відповідь: см².

   Розв’язуючи таку задачу в школі ми дотримуємося І способу, хоча ІІ спосіб за допомогою формули Брахмагупти менш громіздкий, не вимагає обчислення висоти трапеції і такого детального обґрунтування.

 

2.2. Доведення теорем

 

Довести, що площа квадрата дорівнює квадрату його сторони.

Доведення.             Нехай сторона квадрата АВСD дорівнює а. Доведемо, що

В                С            .

1

А                D

Розглянемо перший випадок: розіб’ємо сторону АВ на ціле число п одиничних відрізків. Тоді а=п·1=п. Так само розіб’ємо сторону АD. Через точки поділу проведемо прямі, перпендикулярні АВ і АD. Ці прямі розбивають квадрат АВСD на п·п=п² рівних квадратиків площею 1. Тому

 S _АВСD=п²·1= а²·1= а².

Розглянемо другий випадок: на стороні АВ можна розмістити п одиничних відрізків, але залишається остача – відрізок, коротший від одиничного відрізка. Це означає, що п <  а < п+1. Щоб точніше оцінити площу даного квадрата, поділимо одиничний відрізок на т рівних частин. Тоді довжина кожної такої частини дорівнюватиме , а кількість k. Тепер сторона квадрата лежатиме в межах <  а <.

Площа квадрата зі стороною а лежатиме в межах:

 ()²<  S _АВСD <()². При збільшені кількості точок поділу число т стане як завгодно малим. Площа квадрата АВСD і квадрат числа а лежатимуть у межах, різниця між якими як завгодно мала:

()² - ()²= 2()·+.  А це можливо тільки тоді, коли

 S _АВСD= а².    Теорему доведено.

Ось так доводиться формула площі квадрата у підручнику з геометрії для 8 класу [3]. 

Познайомившись із новими формулами, я вирішила сама довести дану теорему.

Доведення.   Нехай сторона квадрата АВСD дорівнює а. Доведемо, що  .

Оскільки квадрат, це чотирикутник, у якого всі сторони рівні і всі кути дорівнюють по 90⁰, то виконуються усі умови того, що в квадрат можна вписати коло і навколо квадрата описати коло. Тоді для квадрата справджується формула:  .

Значить . Отже, S _АВСD= а², що й треба було довести.   

          На мою думку мій спосіб доведення є набагато простішим і зрозумілішим.