Розв'язування задач по темі "Перпендикулярність прямих і площин у просторі"

Тема:  Розв'язування задач по темі “Перпендикулярність прямих і площин у просторі”

     Мета: формування вмінь учнів застосовувати набуті знання по темі до розв’язування вправ і задач; розвивати вміння працювати самостійно; сприяти активізації розумової діяльності учнів, виникненню внутрішніх мотивів навчання; розвивати бажання застосовувати набуті знання, вміння та навички для досягнення поставленої мети; прищеплювати любов до математики.

     Тип уроку: урок – практикум.

     Девіз уроку (записати на дошці)

“Джерело і мета математики – в практиці”                                                                                    (академік С.Л. Соболєв)

“При вивченні наук приклади корисніші від правил”                                                                                                  (І. Ньютон)

Хід уроку

     І. Організаційний момент.

     На уроці використовується групова навчальна діяльність. Клас поділено на групи. В кожній групі є учні-консультанти, які перед початком уроку перевіряють домашню роботу і теоретичні знання  членів своєї групи.  Під час уроку за правильно виконані завдання і вправи в картку обліку знань виставляють відповідні бали.

     ІІ. Актуалізація . Фронтальна бесіда.

     Можна провести у вигляді дидактичної гри “Ланцюжок”. Група, яка першою дала правильну відповідь на запитання, має право задати наступне запитання і т. д.

1. Дайте означення перпендикулярності прямої і площини.
2. Сформулюйте ознаку перпендикулярності прямої і площини.
3. Що називається відстанню між фігурами?
4. Що називається відстанню від точки до прямої?
5. Що називається відстанню від точки до площини?
6. Що ви можете сказати про відстань від точки до відрізка?
7. Сформулюйте теорему про три перпендикуляри.
8. Які теореми та означення використовуються для доведення теореми про три перпендикуляри?
9. Сформулюйте ознаку перпендикулярності площин.
10.  Яку властивість має основа перпендикуляра, опущеного з точки, яка рівновіддалена від вершин многокутника?
11. Яку властивість має основа перпендикуляра, опущеного з точки, яка рівновіддалена від сторін многокутника, якщо основа перпендикуляра лежить всередині многокутника?
12. Що розуміють під кутом між прямою і площиною?

     ІІ. Розв’язування вправ (усно).

     № 1                                                                     D

                                                                                     C

                                A                                                                B

     ΔABC, º, AC = m, , CD(ABC), CD = n.

     Знайти відстань від точки D до прямої АВ.

     № 2                                                   М

                                                                    К 

                                           В                                           С

                                 А                                        D

     АВСD – квадрат, МК(АВС). Із точки М опустіть перпендикуляри на  сторони АD і СD та діагональ АС.

   № 3                               М

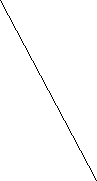
                                             D                             А

                           С                                     В

      АВСD – прямокутник, МD(АВС). Доведіть, що

 (МВС)(МС).

     ІІІ. Розв’язування задач.

Задачі

1. У прямокутній трапеції ABCD бічні сторони дорівнюють 24 см і 25 см, а більша діагональ BD є бісектрисою прямого кута. Із вершини тупого кута С до площини трапеції проведено перпендикуляр СМ довжиною 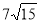см. Знайдіть відстань від точки М до вершини А.
2. У рівнобедреному трикутнику кут при вершині дорівнює 120, а бічні сторони – 10 см. Поза трикутником дано точку, яка віддалена від усіх його вершин на 26 см. Знайдіть відстань від цієї точки до площини трикутника.
3. Діагоналі ромба дорівнюють 12 см і 16 см. Точка М рівновіддалена від сторін ромба і знаходиться на відстані 6,4 см від площини ромба. Знайдіть відстань від точки М до сторін ромба.
4. У паралелограмі  ABCD діагональ BD дорівнює 19 см. Через вершину В проведено площину на відстані 5 см від діагоналі АС. Проекції сторін ВС і АВ на цю площину дорівнюють відповідно 12 см і 9 см. Знайдіть довжину діагоналі АС.
5. Кінці відрізка довжиною 10 см лежать на двох взаємно перпендикулярних площинах. Цей відрізок утворює з площинами кути 30 і 45. Визначити відстань між основами перпендикулярів, опущених із кінців даного відрізка на лінію перетину площин.

     Для економії часу учням пропонується робота з чернетками. Розв’язання задачі на дошці пояснює та група, яка перша розв’язала відповідну задачу.

     Відповіді до задач написані на окремих листках під надрукованими на них буквами. Ці листочки висять на дошці. Учням потрібно  за правильними відповідями вибрати букви і скласти прізвище відомого французького математика. Коли учні складуть одержані букви вийде слово “Лежандр”.

     Лежандр Адрієн Марі (1752 – 1833), французький математик, член Паризької академії наук. Роботи по теорії чисел, теорії елептичних інтегралів, геодезії. Автор класичного курсу елементарної геометрії.

    Історична хвилинка

     Остані три книги “Початки” Евкліда (ХІ – ХІІІ) містять стереометричний матеріал. ХІ книга починається 28 означеннями, серед яких є означення перпендикулярності прямої і площини: “пряма перпендикулярна до площини, якщо вона перпендикулярна до всіх прямих, проведених в площині в точці, в якій вона зустрічає цю площину”.

     Але теореми про три перпендикуляри, яка має велике значення в наш час, у “Початках” Евкліда немає. Вона була доведена математиками Близького та Середнього Сходу. Її доведення є в “Трактаті про повний чотирикутник” Насір ад-Діна ат-Тусі  та тригонометричному трактаті його анонімного попередника. В Європі ця теорема вперше була сформульована Луі Бертраном (1731 - 1812) і доведена в “Елементах геометрії” Лежандра (1794).

ІV. Підсумок уроку.

Учні-консультанти підводять підсумки роботи групи. Підсумовують кількість балів, отриманих учнями за урок.

V. Домашнє завдання.

Оформити задачі в зошитах. Повторити теоретичний матеріал.

Картка обліку знань

Тема: Перпендкулярність прямих і площин у просторі