Розв'язування задач про паралелограм.

Тема. Розв'язування задач про паралелограм.

Мета: доповнити знання учнів поняттями: «достатня та необхідна умови», «критерій»; відпрацювати вміння відрізняти необхідні та дос­татні умови, а також використовувати вивчені необхідні й достатні умови паралелограма до розв'язування задач.

Тип уроку: застосування знань, умінь та навичок.

Наочність та обладнання: конспект «Паралелограм».

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

Якість засвоєння теоретичного матеріалу попереднього уроку мож­на перевірити під час фронтальної бесіди (яку можна провести у формі інтерактивної вправи «Мікрофон»).

Запитання для бесіди

1. Діагоналі чотирикутника АВКМ перетинаються. Чи обов'язково цей чотирикутник є паралелограмом?
2. Точка перетину діагоналей чотирикутника ВСКМ не є серединою однієї з них. Чи може цей чотирикутник бути паралелограмом?
3. Точка М є серединою відрізка КО і BD. Як називається чотирикут­ник BKDО?
4. Відрізки MN і КР паралельні. Чи означає це, що чотирикутник MNKP є паралелограмом?
5. Для чотирьох точок площини А, В, С, К виконується умова АВ =СК. Чи випливає із цієї умови висновок, що точки А, В,С, К є вершина­ми паралелограма?
6. Які відомості треба мати про чотирикутник, щоб зробити висновок про те, що він не є паралелограмом?

Перевірка виконання письмових вправ проводиться вчителем фронтально за зразками (у разі необхідності) або тільки в тих учнів, які потребують додаткової педагогічної уваги.

III. Формулювання мети і завдань уроку

Звернувшись до таблиці 1 (див. Геометрія в таблицях Є. П. Неліна), учні усвідомлюють, що всі твердження, які стосуються загального поняття паралелограма, вони вивчили. Після цього доречно буде ще раз звернутись до конспекту «Паралелограм» та порівняти твердження, що виражають властивості та ознаки паралелограма (див. таблицю). У цьому разі велика ймовірність того, що учні помітять (якщо цього не відбулося раніше), що властивості та ознаки паралелограма є оберне­ними твердженнями. Тому загальну мету уроку можна сформулювати як необхідність з'ясування логічного зв'язку між вивченими власти­востями та ознаками паралелограма, а також подальше формування вмінь застосовувати вивчені твердження про паралелограм під час розв'язування задач.

IV. Актуалізація опорних знань

Виконання усних вправ

1. У чотирикутнику ABCD 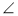A = 30°, 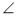C = 50°. Чи може даний чотири­кутник бути паралелограмом? Яка особливість паралелограма (влас­тивість або ознака) використовується для розв'язування цієї задачі?
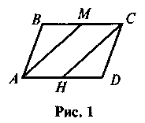
2. ABCD — паралелограм, М — середина ВС, Н — середина AD (рис. 1). Доведіть, що АМСН — паралелограм.
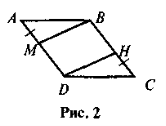
3. ABCD — паралелограм, AM = СН (рис. 2). Доведіть, що DHBM — паралелограм.
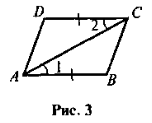
4. На рисунку 3 АВ = CD, 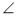1 = 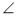2. Доведіть, що ABCD — паралелограм.

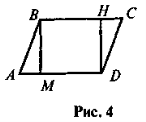
5. АВСD — паралелограм, ВМ 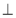АD, DH BС (рис. 4). Доведіть, що ΔABM = ΔCDH.
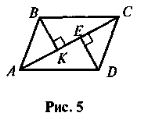
6. ABCD — паралелограм, BK AC, DE AC (рис. 5). Доведіть, що 

ВК = DE.

V. Засвоєння нових знань

План вивчення нового матеріалу

1. Достатня умова.
2. Необхідна умова.
3. Геометричне уявлення про критерій.

 Хоча теоретичний матеріал не є обов'язковим, вивчення питан­ня про необхідну і достатню умову бажано провести на цьому уроці, оскільки правильне уявлення учнів про види математич­них тверджень є однією з умов високого рівня їхньої математич­ної культури, а також запорукою глибокого розуміння загальних математичних закономірностей.

Вивчення нового матеріалу, яке можна провести за підручником, бажано закінчити виконанням низки вправ на перевірку розуміння розглянутих понять, використавши при цьому не тільки матеріал, ви­вчений на уроках геометрії у 8 класі, але й геометричний матеріал 7 кла­су, а також відомості з інших галузей знань (фізики, біології тощо).

VI. Формування первинних умінь

Свідомому розумінню змісту поняття «необхідна та достатня умо­ви» сприятиме розв'язування усних вправ.

Виконання усних вправ

1. Поставте замість крапок слова «необхідно», «достатньо» або «не­обхідно і достатньо», щоб твердження було правильним.

а) Для того щоб чотирикутник був паралелограмом, ..., щоб його діагоналі точкою перетину ділилися навпіл.

б) Для того щоб два кути були суміжними, ..., щоб їхня сума дорівнювала 180°.

в) Для того щоб прямі АВ і CD були паралельними, ..., щоб чотири­кутник ABCD був паралелограмом.

З метою подальшого закріплення знань та відпрацювання вмінь за­стосування ознак та властивостей паралелограма доцільно письмово розв'язати такі задачі.

Виконання письмових вправ

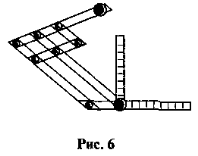
1. У технічному кресленні для побудови паралельних прямих викорис­товують механічну рейсшину (рис. 6). Поясніть принцип її дії.
2. У паралелограмі ABCD бісектриси кутів В і D перетинають діагональ АС у точках Е і F відповідно. Доведіть, що чотирикутник BEDF — паралелограм.

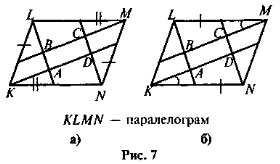
3. Заданими рисунка 7 доведіть, що ABCD — паралелограм.

4* (опорна). Якщо в чотирикутнику протилежні кути попарно рівні, то цей чотирикутник — паралелограм. Доведіть.

VІI. Підсумки уроку

Самостійна робота (теоретична)

Варіант 1

1. Чи існує чотирикутник, кути якого дорівнюють 100°, 80°, 135°, 55°?
2. У чотирикутнику ABCD 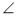A = 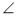С. Чи правильно, що ABCD — пара­лелограм?
3. У паралелограмі ABCD 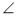A + 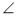C > 180°. Назвіть гострі кути парале­лограма.
4. Діагоналі чотирикутника KLMN перетинаються в точці О, KL = MN,     KL || MN. Назвіть пари рівних відрізків зі спільним кінцем О. Відпо­відь обґрунтуйте.

Варіант 2

1. Чи існує чотирикутник, кути якого дорівнюють 20°, 150°, 10°, 180°?
2. У чотирикутнику ABCD AB = CD. Чи правильно, що ABCD — пара­лелограм?
3. У паралелограмі ABCD 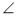B + 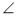D < 180°. Назвіть тупі кути паралело­грама.
4. Діагоналі чотирикутника CDEF перетинаються в точці О, DE || CF,     CD || EF. Назвіть пари рівних відрізків зі спільним кінцем О. Відпо­відь обґрунтуйте.

Варіант 3

1. Чи існує чотирикутник, у якого три кути тупі й один прямий?
2. Чи правильно, що коли в чотирикутнику дві сторони паралельні, а дві інші сторони рівні, то цей чотирикутник — паралелограм?
3. У паралелограмі ABCD з периметром Р  ВС + AD + CD > 0,5Р + АВ. По­рівняйте сторони ВС і CD.
4. Скільки різних паралелограмів можна дістати з чотирьох однакових паралелограмів, якщо прикладати їх один до одного різними спо­собами?

Варіант 4

1. Чи існує чотирикутник, у якого три кути гострі й один прямий?
2. Чи правильно, що коли в чотирикутнику є дві пари рівних, не обов’язково протилежних сторін, то цей чотирикутник — паралелограм?
3. У паралелограмі ABCD з периметром Р 0,5P + CD > BC + AD + AB. Порівняйте сторони ВС і АВ.
4. Скільки різних паралелограмів можна дістати з двох рівних рівнобедрених, але не рівносторонніх трикутників, якщо прикладати їх один до одного різними способами?

VIII. Домашнє завдання

Повторити теоретичні відомості про паралелограм. Виконати до­машню самостійну роботу.

Домашня самостійна робота

1. Один із кутів паралелограма дорівнює 47°. Знайдіть решту кутів.
2. Периметр паралелограма дорівнює 112 см, а дві його сторони від­носяться як 5 : 3. Знайдіть сторони паралелограма.
3. Кут між бісектрисою тупого кута паралелограма і висотою, прове­деною з вершини цього кута, дорівнює 40°. Знайдіть кути паралело­грама.
4. Бісектриса одного з кутів паралелограма ділить його сторону навпіл. Знайдіть периметр паралелограма, якщо ця сторона дорівнює а см.