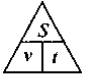
«Розв'язування задач складанням рівняння».

Тема. Розв'язування задач

Мета: сформувати уявлення в учнів про схему розв'язання тексто­вих задач складанням квадратного рівняння; сформувати вміння за­стосовувати складену схему для розв'язування текстових задач.

Тип уроку: засвоєння знань та вмінь.

Наочність та обладнання: опорний конспект «Розв'язування задач складанням рівняння».

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

Зібрати зошити із виконаною домашньою самостійною роботою

III. Формулювання мети і завдань уроку

З метою створення позитивної мотивації навчальної діяльності учнів і усвідомленого сприйняття ними навчального матеріалу, вине­сеного на урок, пропонуємо до їхньої уваги геометричну задачу, на­приклад, на застосування теореми Піфагора.

Задача. Один із катетів на 7 см більший за інший і на 1 см менший від гіпотенузи. Як записати теорему Піфагора для цього трикутника? Знайти сторони трикутника.

Здійснивши нескладні міркування, учні доходять висновку: розв'я­зання задачі неможливе без уведення буквених позначень і вираження величин та співвідношень між ними через ці букви (складання матема­тичної моделі задачі), а також учні усвідомлюють, що математичною моделлю цієї задачі є квадратне рівняння, без розв'язування якого не­можливо знайти невідомі величини. Таким чином формулюється мета уроку: вивчити схему розв'язання задач на складання квадратного рівняння та сформувати вміння застосовувати цю схему на практиці.

IV. Актуалізація опорних знань та вмінь

 З метою успішного сприйняття учнями навчального матеріалу уроку слід активізувати такі знання і вміння учнів: виконання арифметичних дій з дійсними числами та раціональними вираза­ми; складання виразів зі змінними, що відповідають певній умові; записувати у вигляді рівності результат порівняння двох виразів.

Виконання усних вправ

1. Розв'яжіть рівняння: а) а² – 4а + 3 = 0; б) у² – 3у = 0; в) (у – 2)(у + 2) = 0;

г) (у – 3)(у + 2) = 6; д) х⁴ – х² = 0.

2. За даною умовою складіть рівняння:

а) одне число х, друге х + добуток 15;

б) довжина прямокутника а, ширина (а – 2), площа 48 см²;

в) гіпотенуза (прямокутного) трикутника х, катети х – 1 і х – 2.

Як записати теорему Піфагора для цього трикутника?

V. Засвоєння знань

План вивчення нового матеріалу

1. Загальна схема розв'язання задачі на складання рівнянь.
2. Приклади задач на складання квадратного рівняння.

 У вивченні матеріалу уроку слід звернути увагу учнів на такі ключові моменти: по-перше, загальний план розв'язання задач за допомогою рівнянь, вивчений у 7 класі, «працює» і для ви­падку, коли рівняння, що відповідає умові задачі, є нелінійним (квадратним, дробовим...). По-друге, процес розв'язування за­дачі складанням рівняння являє собою свого роду замкнений цикл (задача → математична модель задачі → розв'язок мате­матичної моделі → інтерпретація розв'язку відповідно до умови задачі), тобто за розв'язуванням рівняння обов'язково має йти інтерпретація знайдених коренів рівняння відповідно до умови задачі.

За умови, що учні мають досить високий рівень навчальних досяг­нень,   після  розгляду  прикладів  задач   на  складання  квадратного рівняння можна узагальнити відомості про види задач, які можна роз­в'язувати складанням квадратного рівняння.

VI. Формування вмінь

Виконання письмових вправ

Для реалізації дидактичної мети уроку слід розв'язати завдання та­кого змісту:

1. Арифметичні задачі на складання квадратного рівняння.

1) Добуток двох чисел дорівнює 135. Знайдіть ці числа, якщо одне з них на 6 більше від іншого.

2) Різниця двох додатних чисел дорівнює 23, а їхній добуток до­рівнює 420. Знайдіть ці числа.

3) Добуток двох натуральних чисел, одне з яких на 6 більше від дру­гого, дорівнює 187. Знайдіть ні числа.

4) Добуток двох послідовних натуральних чисел більше за їхню
суму на 109. Знайдіть ці числа.

2. Геометричні задачі на складання квадратного рівняння (на застосу­вання теореми Піфагора, на застосування поняття площі прямо­кутника, квадрата).

1) Знайдіть сторони прямокутника, периметр якого дорівнює 30 см, а площа — 56 см².

2) Знайдіть периметр прямокутника, довжина якого на 4 см більша за ширину, а плота дорівнює 60 см².

3) Від аркуша картону, який має форму квадрата, відрізали смугу шириною 3 см. Площа прямокутної частини аркуша, що залишила­ся, дорівнює 70 см². Визначте початкові розміри аркуша.

3. На повторення: задачі на прямолінійний рівномірний рух, що зво­дяться до лінійних рівнянь.

Із А до В зі швидкістю 12 км/год виїхав велосипедист, а через півго­дини слідом за тім виїхав мотоцикліст зі швидкістю 48 км/год. Мотоцикліст прибув до В на 1 год 15 хв раніше від велосипедиста. Яка відстань АВ?

4. Логічні вправи та завдання підвищеного рівня складності для учнів,
   які мають достатній та високий рівні знань.

1) На змаганнях з баскетболу було зіграно 45 ігор. Скільки команд взяли участь у змаганнях, якщо кожна команда зіграла з усіма іншими по одному разу?

2) Є аркуш картону прямокутної форми, довжина якого в 1,5 раза більше за його ширину. Із нього можна виготовити відкриту короб­ку об'ємом 6080 см³, вирізавши по кутах картону квадрати зі сторо­ною 8 см. Знайдіть розміри — довжину та ширину аркуша картону.

3) Знайдіть пропущене число:

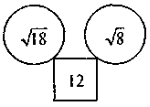
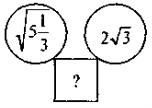
5. На повторення: вправи на розв'язування дробово-раціональних рівнянь.

1) Розв'яжіть рівняння:

а) ; б) ;

в) ; г) .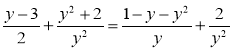

2) Знайдіть значення змінної у, при яких:

а) сума дробів і дорівнює їх добутку;

б) сума дробів і дорівнює їх частці;

в) різниця дробів і дорівнює їх добутку.

VII. Підсумки уроку

В якому випадку правильно виконано записи?

1. Умові задачі: «Одне число х, а друге па 3 більше, їхній добуток до­рівнює 88» відповідає рівняння:

а) х(х – 3) = 88; б) х + (х + 3) = 88; в) х(х + 3) = 88; г) х – (х + 3) = 88.

2. Умові задачі: «Площа прямокутника дорівнює 32 см², сума суміж­них сторін — 12 см. Знайти сторони прямокутника» відповідає рів­няння:

а) х + 32 = х + 12; б) х(12 + х) = 32; в) ; г) х(12 – х) = 32.

VIII. Домашнє завдання

1. Вивчити (повторити) схему розв'язання задач за допомогою квад­ратних рівнянь.
2. Розв'язати задачі на складання квадратних рівнянь.
3. На повторення: вправи на розв'язування дробово-раціональних рівнянь, задачі на рух на складання цілого рівняння з однією змін­ною (7 клас).