Розв'язування задач за допомогою квадратних рівнянь
Про матеріал
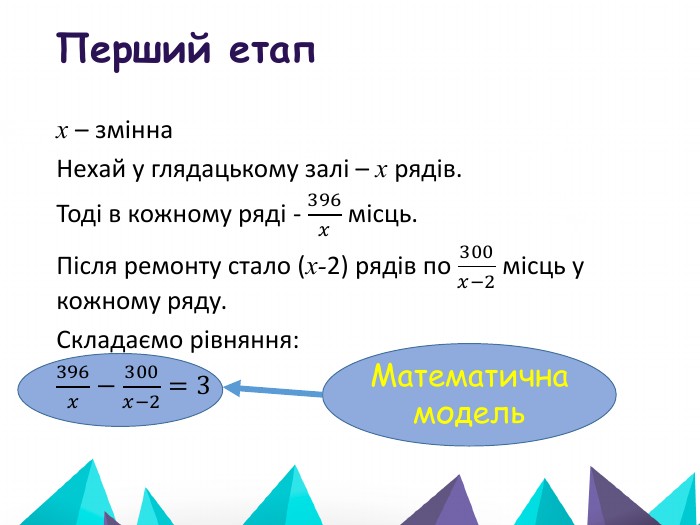
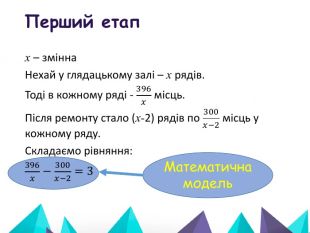
Розв'язування задач на рух, геометричного змісту, на спільну роботу. Приклад кожної задачі учні зустрічають у своєму повсякденному житті. Задачі геометричного змісту мають на меді дати можливість учням навчитися розв'язувати задачі і знаходити невідомі елементи у геометричних фігурах, таких як прямокутник, квадрат, ромб, трикутник і тд. При розв'язуванні задач учні удосконалюють свої знання з розв'язування квадратних рівнянь. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку