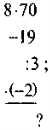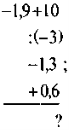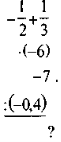Розв'язування задач за допомогою рівнянь

Тема. Розв'язування задач за допомогою рівнянь

Мета: виробити в учнів уміння розв'язувати задачі на рух складан­ням рівнянь; відпрацювати навички розв'язування лінійних рівнянь та виконання арифметичних дій з раціональними числами.

Тип уроку: застосування знань, умінь і навичок.

Хід уроку

I. Організаційний момент

II. Перевірка домашнього завдання

Самостійна робота

Мама отримала премію. На покупку пальта було витрачено усієї премії, а на придбання туфель — премії, залишилось 150 гривень. Ви­значте розмір премії?

III. Відпрацювання знань

Усні вправи

1. Обчисліть:

2. Спростіть вираз:

a) -9m + 3m; б) 0,6b – b; в) т – т; г) -2(а + 3); д) 0,5(-х - 3); є) (3х - 5).

3. Розв'яжіть рівняння:

а) 3х – 2 = х + 3; б) х - 3 = х; в) 2(х - 3) = 4; г) 2(х - 3) = х + 5.

4. Нехай швидкість пішохода а км/год, а велосипедиста — b км/год. Яка
   відстань буде між ними через дві години, якщо:

а) вони вийшли з пункту А одночасно в протилежних напрямках;

б) вони вийшли з пункту А одночасно в одному напрямку;

в) вони вийшли одночасно з пунктів А і В назустріч один одному, і від­
стань від A до В дорівнювала 100 км?

IV. Вироблення вмінь

 Зауважимо, що шестикласники мають певний досвід щодо розв'я­зування задач на рух (у 5 класі таких задач було розв'язано чима­ло). Зараз ми вчимося складати рівняння за умовою задачі. На думку автора, процес складання рівняння та запис необхідних по­яснень піде краще, якщо його супроводжувати складанням та по­ступовим заповненням таблиці (за умови, що S = vt).

Оскільки робота з таблицею є новим елементом, бажано одну із за­дач розв'язати вчителю, а інші запропонувати учням.

Задача 1. Турист 3 год їхав на велосипеді, і 2 год йшов пішки, причо­му пішки він йшов на 6 км/год повільніше, ніж їхав на велосипеді. З якою швидкістю йшов турист, якщо всього він подолав 38 км?

Розв'язання. Складемо таблицю і заповнимо її даними в умові зна­ченнями величин

Бачимо, що за умовою невідомі швидкості і відстань, яку він подо­лав окремо на велосипеді та пішки. Прочитавши питання, бачимо, що шуканою є швидкість руху пішки (до того ж вона менша від швидкості руху на велосипеді). Тому далі позначаємо: нехай х (км/год) — швид­кість руху пішки, тоді х+6 (км/год) — швидкість руху на велосипеді, відстань за 2 год пішки 2х(км), а відстань, яку подолав турист за 3 год на велосипеді, 3(х+6) (км). Разом за 5 год турист подолав 3(х+6)+2х (км), що за умовою задачі становить 38 км. Складемо і розв'яжемо рівняння:

3(х + 6) + 2х = 38; 3x + 18 + 2x = 38; 5x = 20; х = 20 : 5; х = 4.

Отже, швидкість руху пішки 4 км/год.

Відповідь. 4 км/год.

Задача 2. Автомобіль проїхав деяку відстань за 2,5 год. Якби він їхав швидше на 15 км/год, то проїхав би ту саму відстань за 2 год. З якою швидкістю рухався автомобіль і яку відстань він подолав?

Задача 3. Катер пройшов за течією річки відстань від пристані А до пристані В і повернувся назад (від В до А). Швидкість течії 3 км/год. Знайдіть швидкість катера, якщо:

а) від A до В катер йшов 1,5 год, а від В до А — 2 год; б) швидкість ка­тера проти течії річки становить 75 % від швидкості катера за течією.

Додаткова вправа  Виконайте дії: .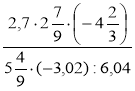

V. Підсумки уроку

Складіть задачу і рівняння до неї за даними таблиці:

Розв'яжіть рівняння.

VI. Домашнє завдання

1. Перший потяг долає відстань між двома містами за 2,5 год, а другий —
   за 3,5 год. Швидкість першого потяга більша від швидкості другого
   потяга на 24 км/год. Знайдіть швидкість кожного потяга та відстань
   між містами.
2. Човен проплив відстань між двома пристанями за течією річки за
   0,6 год, а на зворотний шлях витратив 1 год. Швидкість човна за
   течією річки на 6 км/год більша від швидкості проти течії. Знайдіть
   відстань між пристанями.

Додаткова вправа

Спростіть вираз -4с + 9с – с + 8 і знайдіть його значення при

с = 0; -8; ; -0,25; -2.