Розв’зок логічних задач за допомогою кругів Ейлера

Розв’зок логічних задач за допомогою кругів Ейлера
(На допомогу вчителю математики)

Круги Ейлера — це геометрична схема. З її допомогою можна зобразити відносини між підмножинами (поняттями), для наочного представлення. Метод  Ейлера є незамінним при вирішенні деяких завдань, а також спрощує розмірковування.

Леонард Ейлер був геніальним математиком, який умів застосовувати математичні прийоми на практиці. Він успішно використав для вирішення різних завдань ідею зображення понять і класів предметів у вигляді кіл. Вперше Ейлера їх застосував у листах до німецької принцеси. Він писав тоді, що «кола дуже підходять для того, щоб полегшити наші роздуми». І дійсно, з допомогою цих графіків можна легко і наочно розв’язати завдання, для вирішення яких звичайним способом знадобилося б складання системи з декількох рівнянь, наприклад, з трьома невідомими.

Спосіб зображення понять у вигляді кіл дозволяє розвивати уяву і логічне мислення не тільки дітям, але і дорослим (звичайно, для дорослих підійдуть більш складні завдання). Починаючи з 4-5 років дітям доступно рішення найпростіших завдань з колами Ейлера, спочатку з роз’ясненнями дорослих, а потім і самостійно. Оволодіння методом вирішення завдань з допомогою кіл Ейлера формує в учнів здатність аналізувати, зіставляти, узагальнювати та об’єднувати свої знання для більш широкого застосування.

Приклади розв’язування задач:

1.Із 52 школярів 23 збирають значки, 35 збирають марки, а 16 – і значки і марки. Решта не захоплюються колекціонуванням. Скільки школярів не  захоплюються колекціонуванням?

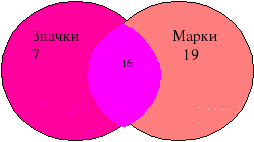
23 - 16 = 7(тільки значки.)

35 – 16 = 19 (тільки марки.)

7 + 16 + 19 = 42(колекціонери)

52 – 42 = 10(не  захоплюються колекціонуванням?)

Відповідь: 10 чоловік.


2. На рисунку круг А зображає всіх співробітників інституту, які говорять на англійській мові, круг Н – на німецькій мові, круг Ф – на французькій. Скільки співробітників інституту говорять:


а) на всіх трьох мовах;

б) на англійській та німецькій мовах;

в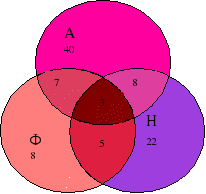) на французькій мові.

Скільки всього співробітників в інституті?

Скільки з них не говорять по французькому?

3. На пікнік поїхали 92 чоловіки. Бутерброди з ковбасою взяли 50 чоловік, з сиром – 60 чоловік, з яловичиною – 40 чоловік, з сиром та ковбасою – 30 чоловік, з ковбасою и  та з яловичиною– 15 чоловік, з сиром и яловичино– 25 чоловік, 5 человіків взяли з собою всі три види бутербродів, а декілька чоловіків замість бутербродів взяли пиріжки. Скільки чоловік взяли з собою  пиріжки?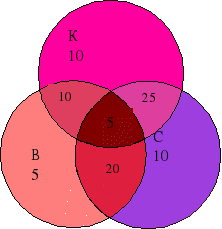 


40 – 35 = 5 (яловичина)

1. 
   60 – 50 = 10 (сир)
2. 
   50 – 40 = 10(ковбаса)

92 – 85 = 7(пиріжки)

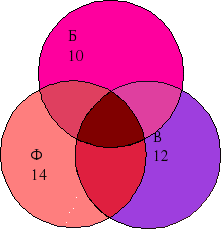
4. Із 54 чоловік 24- займаються баскетболом, 25 – волейболом, 26 – футболом. Секцію по баскетболу та волейболу відвідують 9 чоловік, по волейболу та футболу – 7 чоловік, по футболу та баскетболу – 8 чоловік. Скільки чоловік відвідують всі три секції?






 

1. 
   1.54 – (24 + 25 –9) = 14 (тільки футбол)
2. 
   54 _ (25 + 26 –7) = 10 (тільки баскетбол)
3. 
   54 – (24 + 26 –8) = 12 (тільки волейбол)
4. 
   54 – (14 + 10 + 12) = 18
5. 
   18 –9 = 9
6. 
   (8 + 7) – 9 =6
7. 
   6 : 2 = 3 (всі три секції)

 
Разділ «Раціональні числа»
1. Дана множина: 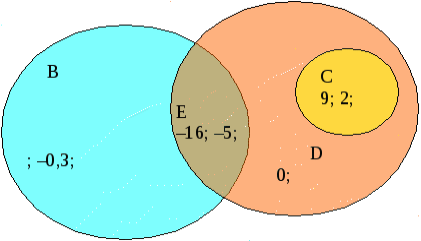А = {–16; ; –0,3; 9; 1; 0; –5; 2; 4,8}.  Складіть з элементів цієї множини  підмножини: 1) В – від’ємних раціональних чисел; 2) С – натуральних чисел; 3) D – цілих чисел; 4) Е – цілих від’ємних чисел. Побудуйте круги Ейлера-Венна множин  A, B, C, D і E.

2. Виберіть з множини  А = {1,5; –7; ; 0; 9; –2; 68} підмножини: 1) В – натуральних чисел; 2) С – цілих чисел; 3) D – раціональних чисел. Побудуйте круги Ейлера-Венна множин А, В, С і D 
3. Выберіть з множини А = {5;  0; –12; –7,8;  –0,95; 8,6; 21; } підмножини: 1) В – додатніх  чисел; 2) С – від*ємних чисел; 3) D – цілих чисел; 4) Е – натуральних чисел; 5) F – невід*ємних цілих чисел; 6) К – від*ємних дробових  чисел. Побудуйте  круги Ейлера-Венна множин  A, B, C і D.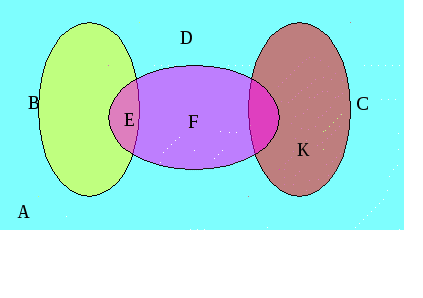 




 

1.«Родинні зв'язки»
По дорзі йшли два батьки і  два сини. А всього три чоловіки.  Чи можлива така ситуація  і як показати це за допомогою кругів Ейлера-Венна? 

Відповідь: По дорозі йшли: батько з сином і своїм батьком .

1.За святковим столом зібралися родичи. Батько оголосив, що сьогодні у нас у   гостях 4 покоління, серед яких 4 мами, 2 діда та  3 батька, 3 бабусі, 5 дітей, а всього 9 чоловік. Відомо, що серед нас 1 прабабуся і тільки 1 жінка є і мамою,і  дочкою і внучкою.  Хто зібрався за святковим столом?



Відповідь:  До дочки прийшли (у неї 2 дітей) в гості батько і мати і її бабуся по лінії мами. В гості  до її чоловіка  прийшли  батько і мати.