Розвиток критичного мислення

Про матеріал

У посібнику розглянуто роль завдань для розвитку критичного мислення молодших школярів на уроках математики. Посібник містить опис деяких теоретичних та практичних аспектів щодо реалізації даної проблеми. Конспекти 2-х нестандартних уроків з математики , проведених у 1 класі. Викладені матеріали, допоможуть вчителям початкових класів, вихователям ГПД ознайомитись з методами роботи, спрямованими на розвиток наскрізного вміння.

Перегляд файлу

ФОРМУВАННЯ І РОЗВИТОК КРИТИЧНОГО МИСЛЕННЯ УЧНІВ НА УРОКАХ МАТЕМАТИКИ

Автор матеріалу.

П,І,Б. Бабич Людмила Іванівна

Посада. Вчитель початкових класів.

Місце роботи. Комунальний загальноосвітній навчальний заклад «Школа І ступеня № 18 м. Бердичева Житомирської області»

У посібнику розглянуто роль завдань для розвитку критичного мислення молодших школярів на уроках математики.

Посібник містить опис деяких теоретичних та практичних аспектів щодо реалізації даної проблеми. Конспекти 2-х нестандартних уроків з математики , проведених у 1 класі.

Викладені матеріали, допоможуть вчителям початкових класів, вихователям ГПД ознайомитись з методами роботи, спрямованими на розвиток наскрізного вміння.

ЗМІСТ

РОЗДІЛ 1. ФОРМУВАННЯ І РОЗВИТОК КРИТИЧНОГО МИСЛЕННЯ УЧНІВ	4
1.1.ПРИЙОМИ ТА СТРУКТУРА РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ НАУРОКАХ МАТЕМАТИКИ	4
1.2.КЛАСТЕР, ЯК ОДИН ІЗ МЕТОДІВ РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ	8
1.3.РОЗВИТОК КРИТИЧНОГО МИСЛЕННЯ УЧНІВ НА УРОКАХ МАТЕМАТИКИ НА ЕТАПІ РЕФЛЕКСІЇ	11
1.4.МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ ЯК ЗАСІБ РОЗВИТКУ КРИТИЧНОГОМИСЛЕННЯ УЧНІВ	14
1.5.ЗАСТОСУВАННЯ ПРИЙОМІВ ІНТЕРАКТИВНОГО НАВЧАННЯ ЯК ЗАСОБУ РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ УЧНІВ НА УРОКАХ МАТЕМАТИКИ	17
1.6.ФОРМУВАННЯ КРИТИЧНОГО МИСЛЕННЯ В ІНТЕГРОВАНОМУ КУРСІ ВИВЧЕННЯ МАТЕМАТИКИ	19
1.7.ТЕХНОЛОГІЇ РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ НА УРОКАХ МАТЕМАТИКИ	22
1.8..РОЗВИТОК КРИТИЧНОГО МИСЛЕННЯ УЧНІВ ПІД ЧАС РОЗВ’ЯЗУВАННЯ ТЕКСТОВИХ ЗАДАЧ НА УРОКАХ МАТЕМАТИКИ	25
1.9..ПРИЙОМИ ФОРМУВАННЯ КРИТИЧНОГО МИСЛЕННЯ УЧНІВ В ПРОЦЕСІ РОЗВ’ЯЗУВАННЯ ЗАДАЧ НА РУХ	27
1.10.ВИКОРИСТАННЯ ТЕХНОЛОГІЇ КРИТИЧНОГО МИСЛЕННЯ У ПРОЦЕСІ ВИВЧЕННЯ ЧОТИРИКУТНИКІВ	30
1.11.РАЦІОНАЛЬНІ ОБЧИСЛЕННЯ ЯК ОДНА З ФОРМ ПРОЯВУ КРИТИЧНОГО МИСЛЕННЯ	33
1.12.ФОРМУВАННЯ КРИТИЧНОГО МИСЛЕННЯ ШКОЛЯРІВ НА УРОКАХ МАТЕМАТИКИ З ВИКОРИСТАННЯМ ГЕОМЕТРІЇ ЯК ЗАСІБ ПІДВИЩЕННЯ МАТЕМАТИЧНИХ ЗНАНЬ	40
РОЗДІЛ 2. ІННОВАЦІЙНІ ТЕХНОЛОГІЇ ЯК ЗАСІБ РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ УЧНІВ НА УРОКАХ МАТЕМАТИКИ	43
2.1.МАТЕМАТИЧНІ КОМП’ЮТЕРНІ ІГРИ ЯК ЗАСІБ РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ УЧНІВ	43
2.2. РОЗВИТОК КРИТИЧНОГО МИСЛЕННЯ УЧНІВ НА УРОКАХ МАТЕМАТИКИ З ВИКОРИСТАННЯМ ЕЛЕКТРОННИХ ЗАСОБІВ НАВЧАННЯ	46
2.3.ВИКОРИСТАННЯ СУЧАСНИХ ПРОГРАМНИХ ЗАСОБІВ НА УРОКАХ МАТЕМАТИКИ	49

ДОДАТКИ

1.Нестандартний урок математики проведений в спортивному залі на тему: «Досліджуємо число і цифру 5. Склад числа 5»

52

2. Нестандартний урок математики на тему:

«Досліджуємо число і цифру 7. Склад числа 7»

56 РОЗДІЛ 1. ФОРМУВАННЯ І

РОЗВИТОК КРИТИЧНОГО МИСЛЕННЯ УЧНІВ

1.1. ПРИЙОМИ ТА СТРУКТУРА РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ НА УРОКАХ МАТЕМАТИКИ

Мета, поставлена перед учнями ХХІ ст., виходить за межі простого засвоєння змісту стандартної шкільної програми. Сьогодні школа повинна допомогти дитині інтегруватися в суспільстві, сформуватися як особистість, знайти та розкрити її здібності, а також навчити боротися з різними ситуаціями, які трапляться на її життєвому шляху. Таким чином вчителі вимушені шукати нові методи організації навчального процесу. Одним з таких є розвиток критичного мислення [4].

Критичне мислення – це процес аналізу, синтезування й обґрунтовування оцінки правильності інформації; здатність генерувати чи змінювати свою позицію на основі фактів й аргументів, коректно застосовувати отримані результати, приймати зважені рішення [2]. Критичне мислення найкраще розвивати на уроках формування умінь та навичок.

Потрібно також розуміти, що критичне мислення ніяк не пов’язане з простим запам’ятовуванням, розумінням складних речей, творчим або інтуїтивним мисленням.

Важливі ключові характеристики, які має критичне мислення: починається з постановки питань та проблем, які потрібно вирішити; інформація є відправною, а не кінцевою точкою для розвитку; самостійність та свобода думки; використовує переконливу аргументацію і докази [3].

Можна пояснити, з чого складається таке мислення і чим воно відрізняється від звичайного [4]. Критичне мислення: чіткість, точність, конкретність, ретельність, значимість, послідовність, глибина (фундаментальність), повнота, значущість, оцінююче судження, зважене судження, класифікація, припущення, розуміння принципів. Звичайне мислення: нечіткість, неточність, невизначеність, похибки, незначимість, непослідовність, поверховість, неповнота, тривіальність, здогадки, імпульсивне віддавання переваги, просте групування, вірування, об’єднання понять за асоціацією.

Працюючи з технологією розвитку критичного мислення стає зрозумілим те, що навчити учнів мислити критично з першого уроку фактично неможливо. Критичне мислення формується поступово, воно є результатом щоденної кропіткої роботи вчителя й учня. Не можна виділити чіткий алгоритм дій учителя з формування критичного мислення в учнів. Але можна виділити певні умови, створення яких здатне спонукати і стимулювати учнів до розвитку критичного мислення [1].

Критичне мислення, перш за все, є інструментом розгляду нескінченного розмаїття існуючих проблем. З точки зору американського філософа і педагога Дж. Дьюї, критичне мислення виникає тоді, коли людина починає займатися конкретною проблемою. Тому головне питання, яке слід поставити з приводу тієї або іншої ситуації, є питання про те, якого роду проблеми це явище породжує. Важливо підкреслити важливість критичного мислення як особливого виду інтелектуальної діяльності, що дозволяє людині зробити вірне судження про запропоновану їй точку зору [4].

Урок критичного мислення має певну структуру та складається з п’яти основних етапів [3].

1.Розминка (головна функція - створення сприятливого психологічного клімату на уроці).

Під час уроку математики вивчають тему «Моделюємо різницеве порівняння». Учні мають назвати, яких вмінь вони вже набули для роботи з математичними виразами, і заповнити разом з учителем першу і другу колонки таблиці «Знаємо – Хочемо дізнатись – Дізнались».

2.Обґрунтування навчання (постановка мети уроку, мотивація вивчення конкретної теми та предмета в цілому).

При вивченні теми «Збільшуємо або зменшуємо на кілька одиниць» пропоную учням подивитися на таблицю і відповісти на запитання «Чому вчених зацікавив даний запис?»

Запитання. Одного разу вчені знайшли в Індії давній математичний рукопис, після розшифровування якого їх зацікавив такий запис [1].

Таблиця 5

10		3
40		12

- Як ви вважаєте, що він означає?

3.Актуалізація (на цьому етапі відтворюються знання, вміння, встановлюється рівень досягнень з теми, що потрібно для наступних етапів уроку).

4. Усвідомлення змісту (учень знайомиться з новою інформацією, аналізує її, визначає особисте розуміння цієї інформації).

Актуальність етапу:

розвиток уміння працювати з інформацією, виділяти головне, суттєве;

- формування компетентностей учнів.

5.Рефлексія(учень стає власником ідеї, інформації, знань; має можливість використати знання, обмінятися ними з іншими учнями; оцінити та самооцінити діяльність).

Актуальність етапу:

усвідомлення зробленого на уроці;
демонстрація знань та їх застосування;
можливість замислитись над підвищенням якості роботи;
розуміння необхідності корекції;
можливість диференціації домашнього завдання.

Кожен з етапів відіграє важливу роль для досягнення мети уроку.

Ключовими етапами формування критичного мислення є виклик (формування та постановка питань), осмислення (ознайомлення з новою інформацією), рефлексія (включення нових понять в уявлення). Для кожного з етапів використовуються певні прийоми [3].

Серед найбільш ефективних прийомів, які сприяють розвитку критичного мислення, на нашу думку, є асоціації, мозковий штурм, кластери, робота в парах [2].

Асоціації. Вчитель пропонує учням по черзі висловитися, про те, які асоціації в них викликає основне поняття уроку. Цим самим учні зможуть «увійти» в тему, згадати те, що вони чули.

Мозковий штурм (до 7 хвилин). Прийом починається постановкою перед учнями чітко сформульованого проблемного питання, яке дає змогу висувати багато версій для відповіді. Усі ідеї для вирішення записуються на дошці та обговорюються в подальшому. Під час процесу учитель може спонукати дітей змінювати думки один одного.

Кластер. Прийом подібний до мозкового штурму, для його застосування потрібно до 5 хв. Він передбачає виокремлення смислових одиниць тексту й графічне оформлення їх у певному порядку у вигляді грона. Кластери допомагають учням у ситуаціях, коли під час письмової роботи запас думок вичерпується. Система кластерів охоплює більшу кількість інформації, ніж ви б могли отримати за звичайної письмової роботи.

Продуктивним прийомом є й обговорення пропонованого проблемного запитання в парах або з використанням прийому «2–4 – всі разом» (до 7–8 хв.). Використовуючи цей прийом, учитель формує запитання та дає учням 1–2 хвилини часу для продумування можливих відповідей або рішень індивідуально. Далі об’єднує учнів у пари і просить їх обговорити свої ідеї один з одним, потім об’єднує учнів у четвірки, де вони обговорюють уже утворені рішення та дають відповідь на загал.

Отже критичне мислення – складне й багаторівневе явище. Мислити критично означає вільно використовувати розумові стратегії та операції високого рівня для формулювання обґрунтованих висновків і оцінок, прийняття рішень.Результат – раціональне використання часу, ефективна робота з джерелами інформації, уміння організувати цю інформацію так, щоб зберегти її ціннісну сутність [4]. Характерною особливістю цього типу мислення є те, що процес міркування нестандартний, відсутній готовий взірець розв’язку. Проблемність забезпечує внутрішню мотивацію навчальної діяльності учнів; спонукає вчителя ознайомити школярів із правилами критичного мислення; потребує використання проблемних методів навчання та інтерактивних занять, а також орієнтує на письмове викладення розв’язків задач та організацію осмислення цих розв’язків. А це означає, що наслідком навчання через критичне мислення виступають особистісні зміни учнів та студентів, тобто їхній розвиток: вони перебудовують свій досвід, здобувають нові знання та способи розв’язування проблемних задач Для кращого розвитку критичного мислення існують спеціальні тренінги, де кожен може спробувати змоделювати заняття з розвитку критичного мислення з використанням конкретних методів, прийомів [1].

Література

1. Пометун О. І. Сучасний урок. Інтерактивні технології навчання / О. І. Пометун, Л. В. Пироженко. – К: А. С. К., 2005.

Маркова І. С. Урок математики в сучасних технологіях: теорія і практика. Розвиток критичного мислення./ І. С. Маркова, Г. О. Біловол. - Х: Основа, 2007.
Критичне мислення: характеристика, вправи на розвиток критичного мислення. [Електронний ресурс] – Режим доступу до ресурсу:
http://etwinning.com.ua/content/files/659841.pdf
European pedagogical studies/ Асоц. ректорівпед. ун-тівЄвропи. –

Київ: НПУ ім. М. П. Драгоманова, 2015, Вип. 5–6.

1.2. КЛАСТЕР, ЯК ОДИН ІЗ МЕТОДІВ РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ

Сучасна освітня система має бути побудована таким чином, аби учням були надані можливості самостійно міркувати, зіставляти різні точки зору, різні позиції, формулювати й аргументувати власну позицію, спираючись на знання фактів, законів, закономірностей науки, на власні спостереження, свій або чужий досвід. Аналіз психологічного дослідження дітей показав, що 20% учнів основної школи мають низьку мотивацію до навчальної діяльності.

Тому ми маємо створити умови для розвитку і реалізації здібностей абсолютно всіх учнів: і з високим потенціалом до навчання, і з відсутністю інтересу до навчання. Технологія розвитку критичного мислення (ТРКМ) основана на творчому співробітництві учня й вчителя, на розвитку у школярів аналітичного підходу до будь-якого матеріалу. Вона розрахована не на запам’ятовування матеріалу, а на постановку проблеми і пошуку її рішення.

Критичне мислення – це здатність аналізувати інформацію за допомогою логіки таособистісно-психологічного підходу для того, аби застосовувати отримані результати, як до стандартних, так і до нестандартних ситуацій, запитань та проблем. ТРКМ включає в себе різні прийоми. Одним із таких прийомів є, так званий, прийом «Складання кластеру_». Його використовують як на стадії виклику або осмислення так і на стадії рефлексії, тобто він може бути способом мотивації до роздумів, до вивчення теми або формою систематизування інформації при підведенні підсумків [3].

Кластерний аналіз – математична процедура, що дозволяє на основі схожості кількісних значень декількох ознак, властивих кожному обʼєкту (наприклад, досліджуваному) будь-якої множини, згрупувати ці обʼєкти в певні класи або кластери. Здійснюється шляхом обчислення відстані між цими обʼєктами насамперед в термінах евклідової метрики.

Метою кластерного аналізу є утворення груп схожих між собою обʼєктів, які прийнято називати кластерами.

Але саме для реалізації ТРКМ кластер — це графічна форма організації інформації, коли виділяються основні смислові одиниці, котрі фіксуються у вигляді схеми з позначенням всіх зв’язків між ними. Він представляє собою зображення,що сприяє систематизації та узагальненню навчального матеріалу.

Правила побудови кластеру дуже прості. Малюємо модель Сонячної системи: зірку, планети і їх супутники. У центрі розташовується зірка – це наша тема. Навколо неї планети - великі смислові одиниці. Зʼєднуємо їх прямою лінією із зіркою. У кожної планети можуть бути свої супутники, у супутників свої зв’язки. Система кластерів охоплює велику кількість інформації.

Опис прийому «Складання кластеру»

Вчитель виділяє із досліджуваної теми ключове поняття і пропонує учням, за визначений час, виписати якомога більше слів або висловів, пов’язаних, на їхню думку, із запропонованим поняттям. Важливо, щоб учні виписували абсолютно усі асоціації, що приходять їм на думку.

1 етап – 2 хвилини. Учні виконують роботу індивідуально.

2 етап – 2 хвилини. Обговорення отриманих записів у групах. Учні виділяють ті результати, які в них збіглися, найбільш оригінальні ідеї та виробляють колективний варіант відповіді.

3 етап – 2-4 хвилини. «Скидання ідей в кошик». Кожна група по черзі називає одне із виписаних висловів. Вчитель фіксує репліки на дошці. Головна умова - щоби діти не повторювали те, що вже сказали інші.

Загальний час виконання: 7 – 8 хвилин [1].

В результаті такої роботи, на дошці формується кластер – виділення смислових одиниць тексту та графічне їх оформлення у визначеному порядку у вигляді грона, що відображає наявні знання учнів з даної теми, що дозволяє вчителю діагностувати рівень підготовки класного колективу, використовувати отриману схему як опору при поясненні нового матеріалу. Сенс прийому «Складання кластеру» полягає в спробі систематизувати наявні знання з тієї чи іншої проблеми.

Складання кластеру дозволяє учням вільно та відкрито міркувати в рамках будь-якої теми. Учень повинен записати по центру аркуша паперу ключове поняття (зірка). Навколо «накидати» слова або речення, що виражають ідеї, факти, образи, відповідні для даної теми (планети). Від зірки малює стрілки-промені в різні боки, які з’єднують тему з цими словами, від яких, в свою чергу, промені розходяться далі (до супутників). На стадії виклику кластер використовують для стимулювання розумової діяльності, на стадії осмислення – дляструктурування навчального матеріалу, на стадії рефлексії – при підведенні підсумків того, що учні вивчили. Кластер може бути використаний також для організації індивідуальної та групової роботи, як в класі, так і вдома.

У роботі з кластерами необхідно дотримуватися таких правил:

Не боятися записувати все, що приходить на розум. Дати волю уяві та інтуїції.
Продовжувати роботу, поки не закінчиться час або не вичерпаються всі ідеї.
Намагатися побудувати якомога більше зв’язків. Ні в якому разі не слідувати за заздалегідь визначеним планом.

Цей прийом розвиває вміння будувати прогнози і обґрунтовувати їх, вчить мистецтву проводити аналогії, встановлювати звʼязки, розвиває навик одночасного розгляду кількох варіантів, що необхідний при вирішенні життєвих проблем. Сприяє розвитку системного мислення.

Залежно від мети організуємо індивідуальну, самостійну роботу учнів або колективну – у вигляді загального спільного обговорення [2].

Література

Методы и приемы технологии критического мышления на уроках математики [Електронний ресурс] – Режим доступу до ресурсу:

https://infourok.ru/metodi -i -priemi -tehnologii -kriticheskogo -mishleniya -na -urokah matematiki -879484.html .

Слепкань З. И. Психолого-педагогические основы обучения математике : метод. пособие / З. И. Слепкань. – К.: Рад. школа, 1983. – 192с.
Технологии и формы развития критического мышления на уроках математики [Електронний ресурс] – Режим доступу до ресурсу:

https://nsportal.ru/shkola/algebra/library/2016/03/31/tehnologii -i -formy -razvitiya kriticheskogo -myshleniya -na -urokah .

1.3 РОЗВИТОК КРИТИЧНОГО МИСЛЕННЯ УЧНІВ НА УРОКАХ МАТЕМАТИКИ НА ЕТАПІ РЕФЛЕКСІЇ

Нинішні події обумовлюють соціальний запит на виховання творчої особистості, здатної, на відміну від людини виконавця, самостійно мислити, генерувати оригінальні ідеї, приймати нестандартні рішення. Але життя підтверджує, що випускники шкіл не завжди здатні самостійно розв’язувати проблеми, їм бракує ініціативи, творчої уяви, винахідливості. Таким чином, розвиток критичного мислення стає найактуальнішим за часів інтенсивних соціальних змін, коли неможливо діяти без постійного пристосування до нових політичних, економічних або інших обставин, без ефективного вирішення проблем, значна частина яких не передбачувана [3].

Психологи стверджують і життя переконує, що найкращі результати у навчанні учням дають активні форми пізнання, коли знання здобуваються самостійно, в творчому пошуку кожного учня. Вчитель не повинен «підносити» дітям матеріал, він має вчити школярів самостійно шукати істину, робити власні висновки, застосовувати свої знання на практиці, тобто розвивати критичне мислення [5].

Для ефективного управління навчальним процесом нам також потрібен постійний зворотний зв’язок з учнями, інформація про виконану роботу та результати діяльності, тобто педагогічна рефлексія.

Навчання проходить набагато успішніше, якщо учень бачить результати виконаної ним роботи, одержує інформацію про параметри роботи, її напрями тощо. Будь-який контроль знань учитель повинен сприймати не як покарання для учня, а як моніторинг результативності навчального процесу. Та й не всі результати можна виміряти кількістю балів. Іноді потрібно, наприклад, визначити рівень аналітичного, логічного, критичного мислення тощо. Необхідні такі методичні прийоми, які б дали змогу забезпечити оперативний моніторинг якості засвоєння навчальної інформації, яку отримали учні, створити оптимальні умови для рефлексії.

Розглянемо деякі методичні прийоми, що ефективно сприяють розвитку критичного мислення на уроках математики.

PRES-formula(ПОПС-формула) за своїм потенціалом інтерактивний прийом, спрямований на рефлексію учнів, створений професором Девідом Маккойд-Мейсоном із ПАР.

Цінність цього методичного прийому полягає в тому, що він дає учням змогу коротко й усебічно висловити власну позицію з вивченої теми.

Розглянемо як реалізовується ПОПС-формула в математиці.

Учням пропонується написати таке:

П – позиція, О – обґрунтування, П – приклад, С – судження.

Але цей прийом не буде методично закінченим, якщо не використати етап рефлексії.

Перше речення має починатися зі слів: «Я вважаю, що...».

Друге речення (пояснення, обґрунтування своєї позиції) починається зі слів: «Тому що...».

Третє речення (зорієнтоване на вміння довести слушність своєї позиції) починається зі слів: «Я можу це довести на прикладі...».

І, нарешті, четверте речення (судження, висновок) починається зі слів: «З огляду на це я роблю висновок про те, що...» [4].

Щоб визначити загальний напрям рефлексії учнів, учитель додає в першому реченні кілька слів, що визначають тему обговорення.

Таким чином ми отримуємо можливість у лічені хвилини отримати лаконічну інформацію про ступінь заглиблення учня в матеріал, розуміння досліджуваних процесів, його моральну оцінку певної події, явища, факту, тощо.

Ще одним ефективним прийомом розвитку критичного мислення, розрахованим на рефлексію учнів є сенкан.

Сенкан – вірш із 5 рядків, написаний за певними правилами. Написання сенкана – це вільна творчість, що активує розумову діяльність школярів, під час підбиття підсумків щодо вивченого матеріалу. Учень повинен знайти й виділити в досліджуваній темі найсуттєвіші елементи, проаналізувати їх, зробити висновки та коротко сформулювати їх [1].

Правила написання сенкана.

Перший рядок – іменник. Зазвичай це ключове слово теми уроку або тема, яку порушив учитель.

Другий рядок – два прикметники, що позначають дві найхарактерніші ознаки цього іменника.

Третій рядок формується з трьох дієслів, що описують найважливіші процеси, що відбуваються з цим іменником.

Четвертий – ключова фраза, найважливіша ідея.

П’ятий рядок – знову іменник, але вже резюме або синонім іменника з першого рядка, метафора.

Наведемо декілька прикладів сенканів з дитячої творчості.

1. Математика 2. Захоплююча, ясна 3. Міркуй, переконуй, доводь. 4. Математика – цариця всіх наук. 5. Знання.

1. Рівняння 2. Гармонійні, багатоголосні 3. Заворожують, дивують, надихають 4. Вони відкрили для мене гармонію математики. 5. Рівності.

Есе в математиці. Саме цей прийом на уроках української мови дає неймовірний зворотний зв’язок після вивчення певних тем.

Есе – твір невеликого обсягу, що розкриває конкретну тему й має підкреслене суб’єктивне трактування, вільну композицію, орієнтацію на розмовне мовлення, прихильність до парадоксів. Написання есе покликане звернути увагу учня на власний досвід із певного питання [2].

Така форма відгуку забезпечує вчителя знаннями про:

критичне осмислення вивчених понять, площа, обєм, рівняння тощо;

розуміння практичного застосування навчання математики;
критичне оцінювання власних можливостей, форми подачі та засвоєння матеріалу, пропозиції тощо.

Наведемо орієнтовні теми для такої форми роботи зі школярами:

1.Прості і складені числа. Розклад на прості множники.

2.Методи розв’язування нерівностей.

3.Системи вимирювання і перетворення між ними.

Кольорова феєрія належить до особливих видів письмової рефлексії у яких задіяні маленькі кольорові папірці (стіки – невеликі кольорові квадрати). Робота зі стіками не вимагає стільки часу й зосередженості, як «великі» письмові форми проведення рефлексії – есе, щоденник тощо. Водночас вона дає змогу зберегти анонімність і не примушує до обнародування власної позиції. У разі використання кольорових стіків можна контролювати зміну настрою класу (або самооцінку власної діяльності учнів) під час уроку або зрозуміти результат емоційного настрою після проведеного заняття [2].

Наприклад, на столі в учнів лежать стіки трьох кольорів що означають: «Я все зрозумів», «Мені дещо незрозуміло», «Мені складно зрозуміти». Під час пояснення нової теми вчитель просить показати стіки, що відповідають рівню розуміння конкретної тематики. Після цього вчитель приймає рішення – продовжити пояснення, повернутися на вихідну позицію і пояснити знову, змінити тактику пояснення, взяти на замітку й попрацювати індивідуально з окремими учнями.

Отже, саме життя вимагає від нас впровадження в практику новітніх методик розвитку критичного мислення на етапі рефлексії [5]. Адже діалоговий характер методик сприяє активізації роботи всіх учнів, дає дітям впевненість в свої силах, поштовх до оволодіння новими матеріалами. Зростає зацікавленість предметом, бажання здобути більш глибинні знання.

Література

Гін А. О. Прийоми педагогічної техніки/ А. О. Гін. – Харків : Веста : Видавництво «Ранок», 2007. – 176 с.
Методичні прийоми на етапі рефлексії[Електронний ресурс]–Режим доступу:http://domanska.ucoz.ua/publ/metodichni_prijomi_na_etapi_refleksiji/1 -1 0 -Технології розвитку критичного мислення учнів / А. Кроуфорд, В. Саул, С. Метьюз, Д. Макінстер; наук. ред., передм. О. І. Пометун. – К., 2008. – 220 с. – [Електронний ресурс] – Режим доступу: http://firstedu.com.ua
Усне опитування – нові старі прийоми [Електронний ресурс]
Режим доступу: http://osvita.ua/school/lessons_summary/proftech/42893/
Формування історичного світогляду учнів шляхом розвитку критичного мислення [Електронний ресурс] – Режим доступу:

http://gayvoroninnovacii.blogspot.com/2015/01/2.html

1.4. МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ ЯК ЗАСІБ РОЗВИТКУ

КРИТИЧНОГОМИСЛЕННЯ УЧНІВ

Сьогодні від школи вимагається виховання творчої особистості здатної самостійно мислити, генерувати оригінальні ідеї, приймати сміливі, нестандартні рішення.

Одним із основних завдань сучасної освіти є формування критичного мислення в учнів. Тому пошук нових можливостей підсилення розвитку критичного мислення. Засобом формування в учнів умінь та навичок критично мислити на уроках математики є математичне моделювання.

Дослідженням теорією розвитку критичного мислення в свій час займалися М. Скрівен, Р. Пол, Е. Гласер, П. Е. Томас та інші.

Математичне моделювання – потужний метод пізнання зовнішнього світу. Аналіз математичної моделі дозволяє проникнути в суть досліджуваних явищ. Математичні моделі використані в усіх сферах життя і діяльності людини. Одними з головних завдань в навчанні є розвиток творчих і дослідницьких здібностей учнів. На уроках математики учні мають займатися дослідницькою роботою при розв’язанні задач. При цьому вони повинні навчитися чітко формулювати завдання й оцінювати отриманий результат [6].

Для моделювання залучаються різні математичні об’єкти: числові формули, числові таблиці, літерні формули,рівняння, нерівності, системи нерівностей, геометричні фігури, різноманітні схеми, діаграми Венна, графи [1].

Математичне моделювання знаходить застосування при вирішенні багатьох сюжетних завдань. Рівняння, що складається за умовами задачі, є її моделлю. Моделюванню слід приділити в школі належну увагу, тому що математичні моделі використовуються для розв’язання сюжетних завдань. При побудові моделі використовується такі операції мислення, як аналіз, синтез, порівняння, класифікація, узагальнення, які є операціями критичного мислення, і сприяють його розвитку. Складання математичної моделі задачі, переклад завдання на мову математики поволі готує учнів до моделювання реальних процесів і явищ у їх майбутній діяльності [6].

Під математичною задачею Л. В. Коваль та С. О. Скворцова розуміють будь-яку вимогу обчислити, перетворити, побудувати, довести або дослідити що-небудь, що стосується кількісних відношень і просторових форм, створених людським розумом на основі знань про навколишній світ. Серед численних математичних задач вони виділяють арифметичні задачі (в нашому випадку суто математичні задачі) на визначення шуканого значення деякої величини, текстові задачі ‒ задачі, сформульовані на природній мові та сюжетні задачі ‒ задачі, в яких описується кількісний бік якихось явищ, подій. За кількістю математичних дій, які потрібно виконати, щоб відповісти на запитання задачі, усі задачі поділяються на прості й складені [1].

Розглянемо задачі в яких математичними поняттями зручно змоделювати зображені предмети з навколишнього середовища [4].

Задача 1. Скільки дощок потрібно, щоб настелити підлогу в кімнаті довжиною 7,5 м і шириною 5 м, якщо довжина дошки 6 м, а ширина 0,25 м?

Дана задача прикладна, бо в ній говориться про поверхню підлоги – нематематичне поняття. Розв’язуючи задачу, ми замінили її іншою: замість поверхні підлоги розглядали прямокутник. А формула для обчислення площі прямокутника є математичною моделлю даної прикладної задачі.

Задача 2. Водопровідний кран погано закритий. За 6 хвилин набігає повна склянка води. Скільки води витече з такого крана за 1 годину, якщо в 1 літрі міститься 5 склянок води?

Це також прикладна задача з практичним змістом. Математичною моделлю цієї задачі є пропорція.

Задача 3. Сім’я з трьох чоловік на добу потребує 51 кг чистого повітря.

Скільки кг повітря потрібно на наш клас?

Це прикладна задача з екологічним змістом. Математичною моделлю до неї є дія ділення.

Задача 4. Корова прив’язана на галявині до кілка мотузкою завдовжки 8

м. Яку площу вона випасає?

Математичною моделлю є круг та формула для знаходження площі круга.

Задача 5. Катер за 4 год. пройшов 24 км за течією річки і 20 км – проти течії. Знайти швидкість течії, якщо власна швидкість катера дорівнює 12 км/год.

Це прикладна задача, бо рух по воді – нематематичне поняття.

Математичною моделлю задачі є рівняння.

Отжекритичне мислення дає інструменти, щоб зробити власне життя більш осмисленим і успішним. Математичне моделювання пов’язане з більшою частиною змістових ліній шкільного курсу математики і тому представляє особливу цінність у справі навчання розв’язанню власне математичних задач. Крім того, математичне моделювання дозволяє розвивати такі особистісні компетентності: навчально-пізнавальні (забезпечується різноманітністю завдань і змістовним коментарем учителя), комунікативні (забезпечується добором нестандартних оригінальних завдань, підтриманням інтересу до вирішення і складання завдань), емоційно-вольові (забезпечується створенням і підтримкою творчої атмосфери під час розв’язання завдань, роз’ясненням необхідності і наполегливості в досягненні поставленої мети), ціннісні (забезпечується формуванням уявлень про неприпустимість списування, підказок, про доброчинність своєчасно наданої допомоги товаришеві).

Література

Балл Г. А. Теорія навчальних задач: Психолого-педагогічний аспект / А. Г. Балл. – М.: Педагогіка, 1990. – 184с.
Кларин М. В. Развитие критического и творческого мышления/
М. В. Кларин. – К. : Школьные технологии, 2004. – 180 с.
Макаренко В. М. Як опанувати технологію формування критичного мислення / В. М. Макаренко, О. О. Туманцова. – Ч:Основа, 2008. – 96 с.
Соколенко Л. О. Збірник прикладних задач з алгебри і початків аналізу: навч.- метод. Посібник для вчителів і учнів10 – 11 кл. серед. шк., ліцеїв та гімназій фіз.-мат. спрямування/Л. О. Соколенко. – К.: Тираж, 1997. – 127 с.
Тягло О. В. Критичне мислення / В. О. Тягло - Х. :Основа, 2008. – 187 с.
Швець В. О. Еволюція математичного моделювання як методу пізнання і навчання / В. О. Швець, М. О. Філімонова // Математика в школі. – 2010. – №4. – С. 22 – 25.

1.5. ЗАСТОСУВАННЯ ПРИЙОМІВ ІНТЕРАКТИВНОГО НАВЧАННЯ ЯК

ЗАСОБУ РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ УЧНІВ НА УРОКАХ МАТЕМАТИКИ

Нині в основу побудови змісту та організації процесу навчання математики в загальноосвітній школі покладено компетентнісний підхід, який передбачає формування в учнів математичної компетентності, що проявляється в готовності та здатності школярів застосовувати свої знання в реальних життєвих ситуаціях, творчо мислити, критично оцінювати різні ситуації.

Ефективність і результативність формування математичної компетентності учнів, розвитку критичного мислення на пряму залежить від вибору форм і методів організації навчання. Пріоритетними в цьому сенсі стають сучасні педагогічні технології, які забезпечують активні форми діяльності учнів, залучають їх до творчого процесу пізнання, дослідження проблем, формування власної думки та самореалізації [1].

Важливу роль у формуванні критичного мислення учнів на уроках математики відіграють інтерактивні технології навчання. Відмінність між ними і звичними організаційними формами полягає у спрямованості навчальної діяльності учнів на досягнення спільної мети, залежність загального успіху від внеску кожного [2].

Інтерактивні форми і методи навчання покликані активувати навчальну діяльність учнів, розвивати пізнавальний інтерес до вивчення предмету та здатність критично мислити. Навчальний процес відбувається за умови постійної, активної, позитивної взаємодії всіх учнів. Нині існує цілий ряд інтерактивних методів та прийомів навчання, серед яких можна виділити наступні: робота в малих групах, навчальні ігри, соціальні проекти й інші позакласні методи навчання. Їх можна використовувати на різних етапах уроку: вивчення й закріплення нового матеріалу (інтерактивна лекція, «учень у ролі вчителя», Сократівський діалог, тощо), обговорення складних і дискусійних питань та проблем («Займи позицію», проектні технології, «Зміни позицію», дебати тощо) закріплення знань через розв’язання проблем («Дерево рішень», «Мозковий штурм»), рефлексія тощо.

Розглянемо приклади застосування прийомів інтерактивного навчання як засобу розвитку критичного мислення учнів :

1.Метод «Побудова асоціативного куща». Озвучується тема уроку, а учні згадують все, що виникає в пам’яті стосовно цієї теми. Спочатку виникають найстійкіші асоціації, потім другорядні. Відповіді фіксуються у вигляді своєрідного «куща», який поступово «розростається».

Цей метод є універсальним на всіх етапах уроку, зокрема під час актуалізації, в основній частині, як засіб перевірки знань.

Наприклад, даний метод можна використати як на уроці вивчення нового матеріалу з теми «Натуральні числа» так і на уроці узагальнення і систематизації з теми «Натуральні числа та дії над ними». В першому випадку завдання: Що ви знаєте про натуральні числа?

Діти згадують все, що вчили на попередніх уроках. У кінці уроку добавляють ще одну «гілку куща» з нового матеріалу.

В другому випадку учні згадують все, що вивчили про натуральні числа та що вміють робити з ними.

Метод «Аналіз ситуацій». Підходить для використання попереднього досвіду учнів з метою розв’язання проблем та розробки ідей.

Розглянемо застосування цього методу на прикладі теми «Числові та буквені вирази»:

Задача 1. Сашко проїхав на велосипеді 60 км за 5 годин та пройшов пішки 15 км за 3 годин. На скільки швидкість хлопця на велосипеді більша, ніж пішки?

Задача 2. Сашко проїхав на велосипеді 60 км за a годин та пройшов пішки 15 км за b годин. На скільки швидкість хлопця на велосипеді більша, ніж пішки?

Питання до класу.

Чи схожа умова задачі 2 на задачу 1?
Чим відрізняється умова задачі 2 від попередньої?
Що спільного будуть мати вирази для розв’язання задач 2 і 1. А чим будуть відрізнятися ці записи?

Даний приклад можна застосувати як на початку уроку, для підведення до теми уроку так і для підведення підсумків.

3. Метод «Кейс». Головне призначення даного методу – розвивати здатність опрацьовувати різні проблеми і знаходити їх рішення, навчитися працювати з інформацією.

Отже, для успішного застосування прийомів інтерактивного навчання як засобу розвитку критичного мислення учнів на уроках математики вчитель має пам’ятати вимоги щодо їх реалізації та чітко дотримуватись їх, учні мають дотримуватись певних правил, які перед ними ставить вчитель. За виконання таких умов урок справді буде ефективним та дієвим, а знання стійкими.

Література

Макаренко В. М. Як опанувати технологію формування критичного мислення / В. М. Макаренко, О. О. Туманцова – Харків: ВГ «Основа», 2008
Пометун О. І. Сучасний урок. Інтерактивні технології навчання / О. І. Пометун, Л. В. Пироженко – К.: А.С.К., 2004 – 192 с.

1.6. ФОРМУВАННЯ КРИТИЧНОГО МИСЛЕННЯ В ІНТЕГРОВАНОМУ КУРСІ ВИВЧЕННЯ МАТЕМАТИКИ

Критичне мислення є особливим типом мислення, який бажано вирізняти серед інших ментальних процесів. Очевидно, що просте запам’ятовування не є критичним мисленням. Запам’ятовування - найважливіша розумова операція, без якої навчальний процес є неможливим, проте воно кардинально відрізняється від критичного мислення. У комп’ютера пам’ять набагато краща, ніж у будь-кого з нас, однак ми розуміємо, що його здатність запам’ятовувати ще не є мисленням. Його також не варто плутати з розумінням складних ідей. Коли ми працюємо над розумінням чужої ідеї наше власне мислення пасивне – ми лише сприймаємо те, що створив хтось інший [2].

Критичне мислення спирається на отриману інформацію, усвідомлене сприйняття власної розумової діяльності та діяльності інших в оточуючому інтелектуальному середовищі. Однак рівень критичності визначається не тільки запасом знань, а й особистісними якостями, установками, переконаннями. Критичність особистості повинна бути напрямлена перш за все на самого себе: на аналіз і оцінку своїх можливостей, особистісних якостей, вчинків, поведінки [2].

Переважна більшість педагогів прагне змінити практику своєї роботи, щоби сприяти активному навчанню учнів і розвитку в них критичного мислення. Вони хочуть, щоб учні не просто запам’ятовували навчальний матеріал, а запитували, досліджували, творили, вирішували, інтерпретували та дебатували за його змістом. Таке навчання сьогодні вважається «найкращою практикою». Дослідження показують, що саме на активних заняттях - якщо їх орієнтовано на досягнення конкретних цілей і добре організовано - учні засвоюють матеріал найбільш повно і з користю для себе. Фраза «найбільш повно і з користю для себе» означає, що учні думають про те, що вони вивчають, застосовують це в ситуаціях реального життя або для подальшого навчання та можуть продовжувати вчитися самостійно. Навчання, результати якого можна використовувати, причому протягом значного часу, - це набагато ефективніший шлях використання часу, ресурсів педагога й суспільства, аніж навчання, що залишає учнів пасивними, стомлює вчителя одноманітністю і результати якого швидко забуваються, оскільки вони не розвиваються та не використовуються на практиці.

Найбільш успішними є заняття, на яких учнів заохочують до активного та критичного мислення, що дозволяє нам обмірковувати власні думки та причини виникнення тієї чи іншої точки зору. Тобто ми міркуємо про те, яким чином приходимо до наших власних рішень або розв’язуємо завдання, проблеми. В цьому випадку наші думки свідомо спрямовані на певну мету. Такі міркування та ідеї ґрунтуються не на наших упередженнях чи забобонах, а на логіці, надійній і достовірній інформації, яка збирається з багатьох джерел. Коли ми мислимо критично і помічаємо помилку чи бачимо інший, кращий спосіб осмислення завдання чи проблеми, ми зацікавлено вивчаємо його. Учні, які мислять критично, зазвичай навчаються з інтересом, навіть у дуже важких інтелектуальних завданнях вони бачать можливості для навчання. Ці учні шукають шляхи застосування навичок критичного мислення і, як правило, охоче їх використовують - і в класі, і в своєму повсякденному житті. Саме завдяки таким учням викладання стає приємнішим і цікавішим для вчителя.

Міжпредметні уроки й навчальні блоки можуть бути створені на основі будь якої конкретної дисципліни з будь-якої точки зору. В ідеалі більшість тематичних навчальних блоків є міжпредметними за своїм характером. Однак, якщо учні будуть чітко розуміти, що в даному навчальному блоці поєднуються два або більше предмети, міжпредметні уроки допоможуть створити контекст для осмисленого навчання. Фаза актуалізації допомагає учням установити зв’язки між поняттями й темами, які були вивчені раніше. Під час фази побудови знань учні повинні інтегрувати й застосовувати знання з різних дисциплін.

Завдання міжпредметного викладання:

вивчати взаємозалежні поняття й принципи через розв’язання завдань;
створити реальні контексти, у яких учні можуть застосувати нові знання;
допомогти учням побачити й відчути на практиці реальні зв’язки між предметами й поняттями в різних предметах;
здобувати нові знання через практичні дослідження в реальних контекстах;
вчитися в обстановці орієнтованої на учня, на основі досвіду, активно й у співробітництві з іншими учнями;
використовувати методи викладання, засновані на «дослідженні».

Активне навчання й критичне мислення відповідають таким цілям:

учні знаходять свої власні значення й смисли.;
учні задають питання, збирають необхідні дані або докази, аналізують ці дані або докази, а також висувають логічні пояснення результатів;
учні вирішують завдання в природних контекстах, користуючись власними методами - учитель лише спрямовує учнів;
учитель надає підтримку на різних рівнях, спрямовує їхню роботу, допомагає структурувати досліджувані ними завдання або питання [3].

Отже можна вважати що для сучасного інформаційного суспільства, що швидко розвивається і базується на сучасних технологіях, характерні новітні політичні технології, новітні засоби інформації, здатні формувати громадську думку, активно впливати на суспільну та індивідуальну свідомість, а іноді й змінювати усе життя суспільства. Усе це потребує від людей здатності не лише орієнтуватися в інформаційних потоках, а й відбирати та оцінювати усе, що надходить ззовні, потребує критичного мислення. А розвивати критичне мислення міжпредметним викладанням набуває значного місце в сучасній системі освіти [2].

Література

Вукіна Н. В. Критичне мислення: як цьому навчати: Науковометодичний посібник за наук. ред. О. І. Пометун / Н. В. Вукіна,
Н. П. Дементієвська, І. М. Сущенко – Харків, 2007. – 190 с.
Козира В. М. Технологія розвитку критичного мислення у навчальному процесі: навчально-методичний посібник для вчителів/ В. М. Козира. – Тернопіль: ТОКІППО, 2017. – 60с.
Кроуфорд А. Технології розвитку критичного мислення учнів/ А. Кроуфор,В.Саул,С.Метьюз,Д.Макінстер;Наук.ред., передм. О. І. Пометун. - К. : Видво «Плеяди», 2006. – 220 с.

1.7. ТЕХНОЛОГІЇ РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ НА УРОКАХ МАТЕМАТИКИ

Розвиток критичного мислення є одним з наскрізних завдань навчально-виховного процесу у новій українській школі. Перед учителем постає завдання підготувати та провести урок, який розвиває критичне мислення учнів. О.І. Пометун зауважує, що для цього слід пам’ятати, що критичне мислення – це неупереджене дослідження предмету або проблеми. Тому урок варто починати, на її думку, з того, що учні мають з’ясувати: що вони вже про це знають; що їм слід вивчити; які запитання постають перед нами у зв’язку з темою уроку. Далі навчальний процес учитель має організовувати так, аби учні вільно виявляли факти, розглядали варіанти розв’язання проблеми, а наприкінці дійшли до підкріпленого фактами осмислення власної позиції щодо поставлених запитань. Щоб підготувати та провести урок з розвитку критичного мислення вчитель має створювати атмосферу позитивної взаємодії учнів, розумітися в тому, які форми й методи навчання ефективніші на певному етапі уроку, а ще – і це принципово важливо – самому мислити критично [2] .

Традиційно, на уроці розвитку критичного мислення виділяють три етапи, що відповідають тим компонентам навчання, які виділяли Ж. Піаже і його послідовники. Фаза актуалізації(передбачення), під час якої педагог спрямовує учнів на те, щоб вони думали над темою, яку починають вивчати і задавали питання. Фаза актуалізації має на меті: актуалізувати у пам’яті учнів вже наявні знання; неформальним шляхом оцінити те, що вони вже знають; встановити цілі навчання; зосередити увагу учнів на темі; представити контекст для того, щоб вони зрозуміли нові ідеї. Фаза побудови знань,під час якої вчитель підводить учнів до постановки питань, пошуку, осмислення матеріалу, відповідей на попередні питання, визначення нових питань і намагання відповісти на них. Ця фаза відбувається в основній частині уроку й має на меті: порівняти очікування учнів з тим, що вивчається; переглянути очікування й висловити нові; відстежити процеси мислення, перебіг думок учнів; зробити висновки і узагальнення щодо матеріалу; поєднати зміст уроку з особистим досвідом учнів; поставити запитання до вивченого на уроці матеріалу. Фаза консолідації, під час цієї фази вчитель прагне, щоб учні відрефлексували те, про що дізналися і запитали себе, що це означає для них, як це змінює їхні попередні уявлення, зрештою як вони зможуть це використовувати. Ця фаза має на меті: узагальнити основні ідеї; інтерпретувати визначені ідеї; обмінятися думками; виявити особисте ставлення [1].

В українській сучасній методичній літературі, щодо підготовки уроку з розвитку критичного мислення, зазначається, що такий урок має складатись із трьох етапів:

Виклик. Мета – формування особистого інтересу для отримання інформації. Учні мають подумати та розповісти іншим про те, що вони знають з обраної теми для обговорення – так отримані раніше знання усвідомлюються і стають базою для засвоєння нових. Задача вчителя на цьому етапі – узагальнити знання дітей, допомогти кожному визначити «своє особисте знання» і основні цілі для отримання нових;
Осмислення. Діти знайомляться з новою інформацією. При цьому вони мають відслідкувати своє розуміння і записувати у вигляді питань те, що вони не зрозуміли – для того, щоб пізніше заповнити ці «білі плями». Після ознайомлення з інформацією кожен учень має сказати про те, які орієнтири чи фрази чи слова допомогли йому зрозуміти інформацію, а які, навпаки, заплутували. Головний принцип етапу осмислення – вчитель має давати учням установку на індивідуальні пошуки інформації з подальшим груповим обговоренням та аналізом;
Рефлексія. Учні мають обдумати те, що вони взнали та як включити нові поняття в свої уявлення; обговорити, як це змінило їхні думки, бачення, поведінку [1] .

Реалізація завдань кожного етапу передбачає використання різноманітних технологій. О.І. Пометун [2], виділила наступний перелік:

Виклик або виступ: кластер, асоціативний кущ, дерево передбачень, таблиця «Знаємо - Хочемо дізнатися - Дізнались», мозковий штурм, робота в парах, кошик ідей, правильні і неправильні судження, мультиголосування, передбачення на основі опорних слів, діаграма Венна.
Осмислення, або основна частина уроку: карта поняття, читаємо в парах/запитуємо(узагальнюємо) в парах, «тонкі» і «товсті запитання, подвійний щоденник, читання з маркуванням, опорні слова, т-таблиця, картографування тексту, концептуальна таблиця, спитайте у автора, ажурна пилка (мозаїка), навчаючи вчуся, дискусія.
Рефлексія, або підбиття підсумків: сенкан, кластер, займи позицію, бортовий журнал, таблиця «Знаємо - Хочемо дізнатися - Дізнались», концептуальна таблиця, ПМЦ, шкала думок, ПРЕС, риб’яча кістка.

Автори посібника «Технології розвитку критичного мислення учнів» [2], відзначають, що вчителі математики часто вірять, що оскільки їх предмет містить мало тексту, то в ньому не можуть використовуватися читання та письмо для критичного мислення. Трьохфазна модель є дуже ефективною, забезпечуючи активацію вже набутих знань та розвиток нового словникового запасу, не говорячи вже про творчий інтерес у фазі актуалізації. Звісно, тут менше тексту у фазі побудови знань ніж в інших дисциплінах, але це вирішено в математиці через інші шляхи представлення нових концепцій та ідей. Фаза консолідації включає в себе менше письма та більше представлення нових проблем, але письмо все ж має важливе значення, хоча й не часто використовується в математиці. На допомогу вчителям математики виділені ефективні методи (технології) навчання математики, що сприятимуть розвитку критичного мислення. Для актуалізації – швидке письмо; семантична карта. Для побудови знань – знаю, хочу дізнатись, дізнався; схема Венна; ажурна пилка (кооперативне навчання); семантичний аналіз ознак. Для консолідації – нова проблема; семантична карта і т.д. [1] .

Отже більшість уроків, що розроблені досвідченими вчителями математики в Україні містять перераховані три етапи, на кожному з яких використовуються підібрані ними інтерактивні технології. Переконані, що якщо на уроці математики буде методично грамотно підібрана система вправ, яка змусить учнів пригадати необхідні знання з даної теми, виділити підзадачі до конкретної задачі, знайти власне вирішення проблеми та обґрунтувати, довести правильність розв’язання; коли у процесі розв’язування задачі будь-яка думка буде перевірятися і відточуватися, що може спричинити суперечку, обговорення, заперечення і обмін думками з іншими, то такий урок приречений розвивати критичне мислення на уроках математики.

Література

Кроуфорд А. Технології розвитку критичного мислення учнів / А. Кроуфорд, Е. Венди Саул, С. Метьюз, Дж. Макінстер, адаптований переклад з анг. / за заг. ред. Олени Пометун. – 2006. Електронний ресурс. Режим доступу: http://www.criticalthinking.expert/shop/tehnologiyi -rozvytku -krytychnogo myslennya -uchniv/
Пометун О. І. Як розвивати критичне мислення в учнів (з прикладом уроку) / О. І. Пометун. Електронний ресурс. Режим доступу: http://nus.org.ua/articles/krytychne -myslennya -2/

1.8. РОЗВИТОК КРИТИЧНОГО МИСЛЕННЯ УЧНІВ ПІД ЧАС РОЗВ’ЯЗУВАННЯ ТЕКСТОВИХ ЗАДАЧ НА УРОКАХ МАТЕМАТИКИ

Одним з основних завдань, що стоять перед сучасною школою, є навчання учнів критично мислити, виховання активного ставлення до здобування знань, розвиток їх інтелектуальних і творчих здібностей.

Питання розвитку критичного мислення учнів завжди знаходилося у центрі уваги психологів (П. П. Блонський, А. В. Брушлінський,

Л. С. Виготський, П. Я. Гальперін, В. В. Давидов, О. К. Дусавицький, Я. А. Пономарьов, С. Л. Рубінштейн) і педагогів (Л. В. Занков, І. Я. Лернер,

В. Ф. Паламарчук, М. М. Скаткін, В. О. Сухомлинський).

Текстові задачі мають досить важливе значення та відіграють величезну роль у навчанні математики. Розв’язування задач виступає і як мета, і як засіб навчання. Уміння ставити і виконувати задачі є одним з основних показників рівня розвитку учнів, відкриває їм шлях оволодіння новими знаннями: знайомитись з новою ситуацією, описаною для розв’язування задачі і т.д.

Іншими словами, при розв’язуванні текстових задач людина набуває математичних знань, підвищує свою математичну освіту. При оволодінні методами розв’язування певного класу задач у людини формується вміння виконувати такі завдання, а при достатньому тренуванні - навички, що підвищує рівень математичної освіти [2].

Текстові задачі використовуються як дуже ефективний засіб засвоєння учнями понять, методів, математичних теорій, як найбільш дієвий засіб розвитку мислення учнів, як універсальний засіб математичного виховання і незамінний засіб формування в учнів умінь і навичок практичного застосуваннях математики. Розв’язування задач служить досягненню цілей, які сприяють розвитку критичного мислення.

Пропонуємо добірку текстових задач, що сприятимуть розвитку критичного мислення:

Задача 1. Два процесори ЕОМ, працюючи разом, обробляють дані за 8 с. Перший з них, працюючи сам, може виконати всю роботу на 12 с. швидше, ніж другий, якщо той працюватиме окремо. За скільки секунд виконати цю роботу другий процесор ЕОМ, працюючи сам [1]?

Задача 2. Дівчата Береза, Верба і Тополя посадили три дерева: березу, вербу і тополю. Жодна з них не посадила дерева, від якого пішло її прізвище. Яке дерево посадила кожна дівчинка, якщо відомо, що Береза посадила не тополю [2]?

Задача 3. Математик, який випадково перебував у невеликому місті, вирішив підстригтися. У місті було лише двоє майстрів, які мали свої перукарні. Математик побачив, що в салоні одного майстра брудно, сам майстер одягнений неохайно і дуже погано підстрижений. У салоні другого майстра було ідеально чисто, а господар його був прекрасно підстрижений. Подумавши, математик пішов підстригатися до першого перукаря. Поясніть причину дивної поведінки математика. Чому він прийняв таке рішення [1]?

Задача 4. Спочатку на ділянці збирав урожай один комбайнер. Через 4 години до нього приєднався другий і за 8 годин спільної роботи вони закінчили збирати урожай з ділянки. За скільки годин міг би зібрати врожай з ділянки кожний комбайнер, працюючи окремо, коли відомо, що першому потрібно було для цього на 8 год більше, ніж другому?

Задача 5. Катер пройшов відстань між пристанями за течією річки за 4 год., а проти течії — за 6 год. Знайдіть власну швидкість катера, якщо швидкість течії 1,5 км/год [3].

Задача 6. В одній пачці 50 сірників, а у другій – 90. З першої пачки щодня використовують 7 сірників, а з другої – 12 сірників. Через скільки днів у другій пачці залишиться сірників удвічі більше, ніж у першій [2]?

Задача 7. Купили українську, німецьку, французьку й англійську марки. Вартість покупки без української марки - 40 гривень, без німецької – 45 гривень, без французької – 44 гривні, а без англійської – 27 гривень. Скільки коштує українська марка [3]?

Задача 8. Для ремонту будинку треба 22000 грн. на фарбу треба 15% всієї вартості ремонту, на шпалери – 20%, на меблі – 40%, а решту на побутову техніку. Допоможіть Маші і ведмедику підрахувати скільки треба окремо грошей на фарбу, шпалери, меблі та побутову техніку[1]?

Отже застосування текстових задач на уроках математики розширює в учнів можливості критично мислити. Кожна задача заставляє задумуватися над правильністю дій в тій чи іншій ситуації, стимулює освоєння учнями досить серйозних тем з математики, що, у підсумку, веде до розвитку критичного мислення. Постійне формування в дитини пізнавальних здібностей з використанням технологій розвитку критичного мислення призводить до того, що учні навчаються самостійно вчитися, критично мислити та використовувати набуті знання в повсякденному житті.

Література

Белешко Д. Т. Методика розв’язування нестандартних математичних задач. Ч. 1 / Д. Т. Белешко, М. А. Віднічук, О.В. Крайчук. — Х. :Вид. гр. «Основа», 2017 – 127 с.
Василевский А. Б. Обучение решению задач по математике / А. Б. Василевский. – Минск: Вышейшая школа, 1988. – 255 с.
Гайштут О. Г. Збірник задач з математики з прикладами розв’язань: Для учнів загальноосвітніх шкіл, ліцеїв та гімназій. / О. Г. Гайштут, П. Р.Ушаков — Кам’янець-Подільский.: Абетка, 2002. —704 с.
Кроуфорд А. В. Технології розвитку критичного мислення учнів / А. Кроуфорд ,В.Саул, С.Метьюз, Д.Макінстер; наук. ред., передм. О. І. Пометун. – К. : Плеяда, 2006. – 324 с.
Тягло О. В. Критичне мислення: Навчальний посібник. / О. В. Тягло — Х . : Вид. група «Основа»: «Триада +», 2008. – 192 с.

1.9. ПРИЙОМИ ФОРМУВАННЯ КРИТИЧНОГО МИСЛЕННЯ УЧНІВ В ПРОЦЕСІ РОЗВ’ЯЗУВАННЯ ЗАДАЧ НА РУХ

Життя висуває суспільний запит на виховання творчої особистості, здатної, на відміну від людини-виконавця, самостійно мислити, генерувати ідеї, приймати сміливі нестандартні рішення, аргументувати власну думку, бути толерантними.

Сьогодні залишається актуальним твердження американського мислителя Джона Дьюї, що фундаментальна мета сучасної освіти полягає не в наданні учням інформації, а в тому, щоб розвивати критичний спосіб мислення, навички дають змогу адекватно оцінювати нові обставини і формувати стратегію подолання проблем, які у них криються [1].

Критичне мислення нині один з модних трендів в освіті. Його розвиток є одним з наскрізних завдань навчальновиховного процесу. Критичне мислення – складне й багаторівневе явище. Мислити критично означає вільно використовувати розумові стратегії та операції високого рівня для формулювання обґрунтованих висновків і оцінок, прийняття рішень [3].

З педагогічної точки зору критичне мислення – це комплекс мисленнєвих операцій, що характеризується здатністю людини: аналізувати, порівнювати, синтезувати, оцінювати інформацію з будь-яких джерел;бачити проблеми, ставити запитання;висувати гіпотези та оцінювати альтернативи;робити свідомий вибір, приймати рішення та обґрунтовувати його.

Цим мисленнєвим операціям можна і необхідно навчати, а далі – вдосконалювати їх, тренувати, як, наприклад, тренують м’язи спортсмени чи техніку гри – музиканти. І саме школа є ідеальним середовищем для цього.

Прийоми можна використовувати на трьох етапах уроків з використанням технології розвитку критичного мислення, а саме:

І етап – актуалізація пізнавальних процесів – «виклик»;
ІІ етап – засвоєння змісту;
ІІІ етап – осмислення (рефлексія) [4].

Керуючись тим, що життєво компетентний випускник школи повинен вміти: співпрацювати у групах, колективі, логічно мислити, порівнювати і аналізувати, робити висновки, критично оцінювати життєву ситуацію і творчо мислити, вибираючи шлях у вирішенні проблем у подальшому житті; ми звернули увагу на можливість розв’язування на уроках математики задач прикладного змісту, зокрема задач на рух.

Розв’язування завдань може будуватися з допомогою використання відомих способів, алгоритмів, а може відбуватися як творчий процес. Цей процес передбачає критичне оцінювання ситуації, переосмислення уже відомої інформації та пошук нової, наявність власної думки і оригінальне її розв’язання.

Задача 1. Об’єкти рухаються в протилежних напрямках. Якщо об’єкти віддаляються один від одного, то відстань між ними збільшується зі швидкістю ν₁ +ν₂. Якщо вони рухаються назустріч, то відстань між ними зменшується зі швидкістю ν₁ +ν₂. [2]

Задача 2. Із Харкова і Львова назустріч один одному вийшли одночасно два потяги. Швидкість одного потяга 50 км/год, а другого – 60 км/год. Вони зустрілися через 9,4 години. Знайти довжину колії, якою рухались потяги.

Розв’язання.

5060110 (км) – на стільки зменшується відстань між поїздами за 1 год.
1109,4 1036 (км) – довжина залізниці.

Відповідь: 1034 км. [2]

Задача 2. Об’єкти рухаються в одному напрямку (див. рисунок).

а) ν₁> ν₂. Відстань зменшується зі швидкістю ν₁– ν₂.

б) ν₁< ν₂. Відстань збільшується зі швидкістю ν₂ – ν₁. [2]

Задача 3. Двоє велосипедистів виїхали назустріч один одному з пунктів А і В. Вони рухалися з постійними швидкостями і після прибуття відповідно до В та А відразу ж повернули назад. Перша їх зустріч відбулася за 8 км від пункту В, а друга – за 6 км від пункту А та через 1 год. 20 хв. після першої зустрічі.

Знайдіть відстань між А і В та швидкість велосипедистів.

Текст задачі – це її модель. Можна зобразити також і рисунок до задачі, показавши окремі «стоп-кадри» руху велосипедистів. Але і ця модель – назвемо її наочною – навіть у динамічному варіанті не дасть уявлення про співвідношення між елементами предметної області задачі, про її математичний зміст. Скористаємося варіантом побудови такої моделі [7]. Позначимо через x відстань між пунктами А і В, а через y – час руху велосипедистів до першої зустрічі. Розділивши всю задачну ситуацію на дві частини – до першої зустрічі та між першою та другою зустрічами велосипедистів – визначимо структурну модель першої частини задачної ситуації (Табл. 1) [6].

Таблиця 1

	Шлях		Швидкість		Час
Перший	?	=	?	*	y
	+		\| \|		\| \|
Другий	8	=	?	*	y
	\| \|
	x

Отже, в даному випадку структурна модель задачі представляла собою таблицю із зображенням елементів предметної області задачі та зазначеними зв’язками між ними. Складання подібних моделей дає змогу учням краще розуміти саму суть задачі та критично мислити над її розв’язанням [7].

Критичне мислення спирається на уявлення і є засобом породження оригінальних ідей. Критичне мислення допускає, що на одне запитання може бути більш ніж дві відповіді. Воно є найважливішим елементом творчої діяльності та повсякденного життя.

Література

Технологія розвитку критичного мислення [Електронний ресурс] – Режим доступу до ресурсу: http://konserg.ucoz.ua/load/28 -1 -0 -674 .
Збірник задач на рух [Електронний ресурс] – Режим доступу до ресурсу:http://klasnaocinka.com.ua/uk/article/zbirnik -zadach -na -rukh -2.html
Авершин А. О. Формування критичного мислення у студентів інженерно-педагогічних ВНЗ/А. О. Авершин, Т. В. Яковенко//Збірник наукових праць:Проблеми інженерно-педагогічної освіти. – 2009. – №24–25. –С. 134–145.
Макаренко В. М. Як опанувати технологію формування критичного мислення / В. М. Макаренко, О. О. Туманцова. – Харків: ВГ «Основа», «Тріада +», 2008.
Ріжняк Р. Я. Використання евристичних алгоритмів та модельних перетворень у процесі розв’язування текстових математичних задач / В. Кушнір, Г. Кушнір, Р. Ріжняк//Математика в школі.–2009.–№1 – 2.–С. 17–22.
Ріжняк Р. Я. Моделі задач на рух у 4-5 класах / Р. Я. Ріжняк // Радянська школа. – 1989. – № 10. – С. 35–39.
Швець В. О. Математичне моделювання як змістова лінія шкільного курсу математики / В.О. Швець // Дидактика математики : проблеми і дослідження : міжнародний збірник наукових робіт. – Донецьк : Вид-во ДонНУ, 2009. – № 32. – С. 16-23

1.10. ВИКОРИСТАННЯ ТЕХНОЛОГІЇ КРИТИЧНОГО МИСЛЕННЯ У

ПРОЦЕСІ ВИВЧЕННЯ ЧОТИРИКУТНИКІВ

Як відомо, у шкільній освіті існує безліч методів навчання, різні типи уроків, які переслідують одну єдину мету – засвоєння знань учнями.

Найбільш успішними є заняття, на яких учнів заохочують думати самостійно і критично мислити. Критичне мислення дозволяє нам обмірковувати свої власні думки й причини появи тієї чи іншої точки зору. Це означає, що ми обдумуємо те, яким чином приходимо до наших власних рішень або розв’язуємо завдання, проблеми. Це означає також, що наші думки свідомо спрямовані на певну мету. Такі міркування та ідеї ґрунтуються не на наших упередженостях або забобонах, а на логіці, надійній і достовірній інформації, яка збирається з багатьох джерел [4].

Суть і мета застосування технології критичного мислення такі: освіта не дається вчителем, вона одержується самим учнем. Для цього вчитель має сам оволодіти новим мисленням, відповідним чином сприймаючи зміст навчального матеріалу, вибирати й застосовувати саме ті методи й прийоми навчання, які сприятимуть розвитку критичного мислення учнів. Проблема розвитку критичного мислення є досить актуальною для підвищення якості математичної освіти [3].

Технологія проведення уроку з розвитку критичного мислення традиційно складається з трьох основних частин: вступної, основної та підсумкової.

Вступна частина уроку триває зазвичай перші 5-7 хвилин. За цей час необхідно актуалізувати опорні знання – отримати їх з довготривалої пам’яті учнів. Саме слово підказує, що необхідно «зробити щось актуальним, потрібним» на час саме цього уроку. Опорними такі знання учнів є тому, що саме на них, як на фундаменті, опорі, будуються наступні знання. Вступна частина уроку з розвитку критичного мислення завершується тим, що учитель озвучує нову тему і результати, яких слід досягнути, та стимулює учнів до усвідомлення їхніх власних цілей навчання [5].

Наведемо приклад вступного завдання для уроку на тему «Дельтоїд». З метою розвитку критичного мислення учнів та актуалізації їхніх опорних знань доцільно, на наш погляд, запропонувати їм таке завдання: сформулювати означення чотирикутника та назвати їх види, вказати ознаки кожного виду чотирикутника.

Обговорюючи спільно з учнями ці запитання учитель організовує їх активну діяльність, зокрема, спонукає досліджувати чотирикутники, краще осмислювати ознаки кожного його виду, правильно відповідати на раніше поставлені запитання і ставити свої та, що важливо, шукати на них відповіді тощо. Головне завдання учнів – конструювати знання і навички, формувати власне ставлення до теми чотирикутники.

Основна частина уроку з теми може тривати до 30 хвилин. І коли учень долучається до сприйняття нової інформації з даної теми під час, наприклад, читання тексту, перегляду фільму, прослуховування лекції вчителя, він навчається відстежувати своє розуміння нового й не ігнорувати прогалини в ньому. При цьому важливо, щоб він записував те, що не зрозумів з даного матеріалу, аби з’ясувати це в майбутньому. Подальше відпрацювання й закріплення учнем нових знань відбувається за допомогою різноманітних методів і прийомів організації активної самостійної роботи.

Обов’язкові елементи розвитку критичного мислення в учнів – індивідуальний пошук та обмін ідеями в групах чи загальному колі [2].

Тому під час уроку можна використати такі методи: читання в парах (запитання в парах); передбачення з опорними словами; запитання до вчителя у вигляді мозкового штурму.

Третій етап уроку – підсумковий – найважливіший для розвитку критичного мислення в учнів, бо його основними завданнями є узагальнення, систематизація(але не відтворення!)вивченого й рефлексія щодо процесу і результатів навчальної діяльності. Необхідно, щоб учні подумали про те, що вони дізналися, чого навчилися, запитали себе, що це для них означає, як це змінює їхнє бачення і як вони можуть це використовувати.

Зазвичай підбиття підсумків триває до 10 хвилин. За цей час учні разом з учителем:

узагальнюють та інтерпретують основні ідеї уроку, чи була дана тема цікавою і корисною;
ставлять перед собою запитання, які нові знання отримали вивчаючи тему дельтоїд;
оцінюють набуті знання й уміння по темі дельтоїд, показують спільні і відмінні ознаки з іншими видами чотирикутників та розглядають його

властивості;

планують застосування вивченого на практиці, зокрема, який предмет можна сконструювати, беручи за основу дельтоїд.

Учитель може вдало поєднувати роботу над предметним матеріалом із розвитком критичного мислення учнів. Проте побудова такого уроку вимагає багатьох знань і вмінь від самого вчителя. Так, він має створювати атмосферу позитивної взаємодії учнів, розумітися в тому, які форми й методи навчання ефективніші на певному етапі уроку, а ще – і це принципово важливо – самому мислити критично.

Література

Раухман А. С. Геометрія чотирикутника / А. С. Раухман, В. О. Тадеєв. – Тернопіль: Навчальна книга – Богдан, 2010. – 152 с.
Розвивати критичне мислення в учнів на уроках математики [Електронний ресурс] – Режим доступу до ресурсу: http://radkoruslan73.blogspot.com/2017/03/blog -post.html .
Розвиток критичного мислення у навчальному процесі [Електронний ресурс] – Режим доступу до ресурсу:

https://studopeda.su/17_21875_rozvitok -kritichnogo -mislennya -u -navchalnomu protsesi.html .

Технології розвитку критичного мислення учнів / А. Коуфорд, В. Саул, С. Метьюз, Д. Макінстер // переклад публікації проекта «Читання і письмо для критичного мислення». – 2006.
Як розвивати критичне мислення в учнів [Електронний ресурс] – Режим доступу до ресурсу: http://nus.org.ua/articles/krytychne -myslennya -2/.

1.11. РАЦІОНАЛЬНІ ОБЧИСЛЕННЯ ЯК ОДНА З ФОРМ ПРОЯВУ

КРИТИЧНОГО МИСЛЕННЯ

Розвиток критичного мислення сьогодні є одним із найважливіших завдань у процесі формування особистості, адже людина, що володіє таким типом мислення може завжди об’єктивно оцінювати ту чи іншу ситуацію, адаптувати свою поведінку до умов, що виникли, та використати ті свої можливості, які будуть найбільш доцільними та вигідними.

В русі швидких змін суспільство вимагає від нас високого рівня мобільності та самостійності, тому в школах, там, де починається формація особистості, вчителі повинні виділяти достатньо часу і сил на розвиток критичного мислення, зокрема, найбільшу увагу варто звертати на уроках математики.

Сьогодні, у час стрімкого розвитку технологій, для учнів не є проблемою взяти калькулятор та порахувати різної складності приклади, але вміння виконувати усні чи письмові раціональні розрахунки, працюючи з громіздкими числами, без допомоги техніки, свідчить про високий рівень розвитку критичного мислення, адже саме такий підхід вимагає від учнів пошуку нових способів, які, можливо, не нав’язувались вчителем, але є більш логічно доцільними в даній ситуації, аніж використання стандартних методів.

В процесі дослідження критичного мислення, різні науковці підходили до його визначення по-різному. Так, канадський вчений Ральф Х. Джонсон стверджував, що критичне мислення – це «особливий вид розумової діяльності, що дозволяє людині винести раціональне судження щодо запропонованої їй точки зору або моделі поведінки» [1, с. 15], а український науковець О. І Пометун визначає критичне мислення як здатність людини усвідомлювати власну позицію з того чи іншого питання, вміння знаходити нові ідеї, аналізувати події і оцінювати їх, приймати ретельно обдумані, зважені рішення стосовно будь-яких думок і дій [2]. Багато інших вчених,таких як: Г. Липкіна, Л. Рибак, О. Тягло, М. Ліпман та ін. зробили свій внесок у дослідження критичного мислення як важливої складової у процесі формування особистості і, зрозуміло, тлумачували це поняття по-своєму.

Проаналізувавши усі твердження, можна сказати, що критичне мислення – це, насамперед, вміння самостійно обирати спосіб вирішення тієї чи іншої ситуації, опираючись на чіткі аргументи та минулий досвід, синтезувати та узагальнювати отриману інформацію, вибираючи найбільш вигідну для себе.

На сьогодні, навчальна програма з математики вимагає від учнів не так вміння вивчити або «зазубрити» теоретичний матеріал, а, швидше, зуміти самостійно застосовувати набуті знання, вибираючи ті шляхи розв’язання, які будуть найбільш обґрунтованими та раціональними.

Вчитель, в свою чергу, під час навчально-виховного процесу повинен звертати увагу на ті фактори, які найбільшим чином впливатимуть на свідомість учня, тим самим, формуючи основні засади розвитку критичного мислення. Нестандартні підходи до проведення уроку, пошук та впровадження інноваційних способів та методів розв’язання, вимкнення авторитарного режиму вчителя – все це дасть учням простір для власного дослідження, свободу вибору дій, їх послідовності, сприятиме вихованню самостійних та творчих особистостей.

Звісно, більш звичним є використання цікавих математичних задач, що сприятимуть розвитку критичного мислення на уроках математики в молодшій школі, тому виникають деякі складнощі з вибором вправ для старшокласників, але навіть найпростіші вправи на обчислення можуть допомогти з вирішенням цієї проблеми.

Формування навичок раціонального обчислення – це важкий процес, який вимагає чіткої роботи вчителя та створення всіх необхідних умов для продуктивної роботи учнів.

Цікавий спосіб множення "на пальцях"

1.Таблиця множення на 9

Чи потрібно вчити таблицю множення? Діти цього, як правило, терпіти не можуть. І правильно роблять. Ні до чого її вчити! Але не поспішайте обурюватися. Ніхто не стверджує, що таблицю не потрібно знати. Її винахід приписують Піфагору, але, швидше за все, великий математик лише надав закінчену, лаконічну форму того, що вже було відомо. На розкопках стародавньої Месопотамії археологи знайшли глиняні таблички з сакраментальним: “2·2”. Люди давно користуються цією надзвичайно зручною системою обчислень і відкрили безліч способів, які допомагають осягнути внутрішню логіку і красу таблиці множення, зрозуміти – а не тупо, механічно зазубрити.

Математика – це наука «думаючого мозку» і вчити її потрібно, враховуючи, що існує безліч схем і алгоритмів для розв’язування того чи іншого питання.

У стародавньому Китаї таблицю починали вчити з множення на 9. Так простіше, і не в останню чергу тому, що множити на 9 можна “на пальцях”.

Розглянемо цей спосіб. Покладемо обидві руки на стіл долонями вниз. Позначимо перший зліва палець – 1, другий – 2 і т.д., як це показано. Щоб помножити довільне число від 1 до 9 на 9, подивимось на руки.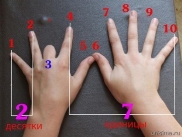

Припустимо, що потрібно знайти добуток 9·3. Згинаємо палець, який відповідає числу, на яке множимо число 9 (тобто третій), рахуємо пальці до загнутого пальця (в нашому випадку – це 2), потім рахуємо пальці після загнутого пальця (в нашому випадку – 7). Пальці до загнутого означають десятки, після загнутого одиниці, тому отримали число 27.

2. Множення на 6, 7 і 8

Розглянемо спосіб, як помножити два числа від 6 до 10. Операція множення проводиться за такою схемою. Подумки пронумеруйте пальці рук наступним чином: повертаємо кисті рук лодонями до себе і позначимо кожен палець руки від 6 до 10 починаючи з мізинця.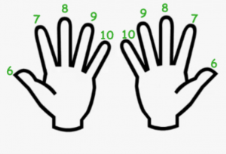

Розглянемо множення 7·8.

Для цього з’єднаємо палець №7 лівої руки з пальцем №8 правої. А тепер порахуємо пальці: кількість пальців під з’єднанням (у нашому випадку 5) — це 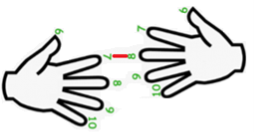десятки.

Кількість пальців лівої руки, що залишилися зверху (разом з зєднанням), множимо на пальці, що залишилися зверху (разом з зєднанням) правої руки — це і буде число одиниць (3·2=6). Отже добуток чисел 7 і 8 дорівнює 56.

Якщо при множенні «одиниць» у результаті маємо число більше 9, то додаємо його десятки до попередніх десятків.

Це лише один з найпростіших прийомів “пальцевого” множення. Їх багато. “На пальцях” можна оперувати числами до 10 000!

У “пальцевої” системи є бонус: її можна сприймати як веселу гру. Охоче займаючись обчисленнями, отримуємо масу позитивних емоцій і в результаті швидко починаємо виконувати всі операції усно, без допомоги пальців

3. Множення натуральних чисел

Для швидкого множення натуральних чисел можна використовувати розподільний та сполучний закони відносно додавання чи віднімання.

Розглянемо застосування цих законів.

9·419=9· (400+10+9)=9·400+9·10+9·9=3600+90+81=3771

7·194=7· (200–6)=7·200–7·6=1400–42=1358

Найбільш легким способом, як швидко навчитися усно множити великі числа, є перемножування десятків і одиниць. Спочатку множаться десятки двох чисел, потім по черзі одиниці і десятки. Чотири отриманих числа додаються.

Для використання цього методу важливо вміти запам’ятовувати результати множення і складати їх усно.

Розглянемо множення 38 на 57, для цього необхідно:

Розкладемо множники на суму двох доданків (30+8)·(50+7);
30·50 = 1500 – запам’ятати цей результат;
30·7 + 50·8 = 210 + 400 = 610 – запам’ятати цей результат;
(1500 + 610) + 8·7 = 2110 + 56 = 2166

Застосовуючи сполучний закон, легко обчислювати добутки чисел, якщо одне з них парне, а інше легко приводиться до числа з нулями (у нашому випадку 125):

32·125 це 16·250 це 8·500 це 4·1000 = 4000

Тобто одне з них зменшуємо у 2 рази, а інше збільшуємо у 2 рази. При цьому отримуємо рівність: 32·125=16·250=8·500=4·1000 = 4000.

Якщо ж це не так важко, то чому б не навчитися таким обрахункам.

4.Множення на 5

Для більшості людей множення на 5 не складає труднощів для невеликих чисел. Щоб швидко порахувати великі числа, помножені на 5 потрібно взяти це число і розділити на 2. Якщо результат – ціле число, то додайте до нього 0 в кінці, якщо немає, відкиньте залишок і додайте 5 в кінці:
1248·5 = (1248/2) _ (0 або 5) = 624_ (0 або 5) = 6240 (результат ділення на 2 ціле число)

4469·5 = (4469/2) _ (0 або 5) = (2234.5) _ (0 або 5) = 22345 (результат ділення на 2 число з залишком)

Або щоб помножити число на 5, треба його помножити спочатку на 10, а потім поділити на 2.

Наприклад :

138·5 = ( 138·10 ) : 2 = 1380 : 2 = 690

548·5 = ( 548·10 ) : 2 = 5480 : 2 = 2740

Щоб помножити число на 5, 25 чи 125 можна поділити його на 2, 4, 8 відповідно і в результаті помножити на 10, 100, 1000. Наприклад:

46·5=46:2·10=230

48·25=48:4·100=1200

32·125=32:8·1000=4000.

Якщо множник не ділиться націло на 2, 4, 8 , то ділення буде з остачею. Тому частку слід помножити на 10, 100, 1000, а остачу на 5, 25, 125. Наприклад:

53·5=26·10+1·5=265

43·25=10·100+3·25=1000+75=1075

66·125=8·1000+2·125=8000+250=8250

5.Множення на 4

Це дуже проста і, з першого погляду, очевидна фішка множення будь-якого числа на 4 – щоб просто помножити будь-яке число на 4, потрібно помножити його на 2, а потім знову помножити на 2:
67·4 = 67·2·2 = 134·2 = 268

214·4 = (214·2)·2 = 428·2 = 856

537·4 = (537·2)·2 = 1074·2 = 2148

Або 58·4 = (58·2) + (58·2) = (116) + (116) = 232

6. Множення чисел на 11

Припустимо, нам потрібно помножити 12 на 11. Візьмемо двозначне число, яке потрібно помножити на 11 і уявимо між його двома цифрами місце, на яке запишемо суму його цифр: 1+2 =3. Одержимо число132, тобто 13·11=132.

Аналогічно, 36·11=396, оскільки 3+6=9.

Щоб помножити на 11 число, сума цифр якого 10 чи більше 10, треба подумки 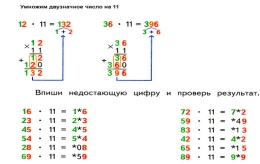розсунути цифри цього числа, поставити поміж них суму цих цифр, та до першої цифри додати 1, а другу і останню (третю) цифру залишити без зміни.

59·11 = 649 (суму двоцифрового числа (5 + 9 = 14) перекидаємо одиницю вліво (5 + 1 = 6), так як сума більша 9. Цифру 4 записуємо в середину).
78·11 = 7 (7 + 8) 8 = 7 (15) 8 = 858;

94·11 = 9 (9 + 4) 4 = 9 (13) 4 = 1034.

79·11 = 869 (7_ (7 +9) _9 ; (7 +1) _6_9)

Припустимо, нам потрібно помножити 124 на 11. Візьмемо число, яке потрібно помножити на 11 і уявимо між його першою і останньою цифрами місце, на яке запишемо суму його цифр починаючи з права на ліво: 2+4 =6 (сума одиниць і десяток числа 124) потім 1+2 =3 (сума десяток і сотень числа 124). Одержимо число1364, тобто 124·11=1364.

Аналогічно, 3765·11=41415

Щоб помножити двоцифрове число на 111, слід справа наліво записати послідовно останню цифру числа (тобто цифру з розряду одиниць), далі суму цифр числа, знову суму цифр числа і першу його цифру. Якщо сума цифр більша ніж 9, то записуємо цифру одиниць, а кожного наступного результату додаємо 1. Наприклад:

42·111==4662.

68·111==7548

Цікаві результати отримаємо в аналогічних добутках.

1·1 = 1
11·11 = 121
111·111 = 12321
1111·1111 = 1234321
11111·11111 = 123454321
111111·111111 = 12345654321
1111111·1111111 = 1234567654321
11111111·11111111 = 123456787654321
111111111·111111111 = 12345678987654321

Щоб помножити двоцифрове число на, можна спочатку його помножити на а, а потім на 11.

Щоб двохзначне число помножити на 22, 33, 44, 55, 66, 77, 88, 99, треба цей множник подати у вигляді добутку однозначного числа на 11. Спочатку виконуємо множення на однозначне число, а потім на 11:

123·55=(123·5) ·11=615·11=6765

15· 33 = 15 · 3 · 11 = 45 · 11 = 495

23· 66 = 23· 6 · 11 = 138· 11= 1518

7. Множення на 9, 99, 999

Щоб помножити число на 9, 99, 999 можна до числа дописати стільки нулів, скільки дев’яток у другому множнику, а від результату відняти число. Наприклад:

286·9=2860–286=2860–300+14=2574

23·99=2300–23=2300–23=2277

18·999=18000–18=17982

8. Множення на 15.

Якщо число парне, то до числа додати його половину і приписуємо нуль:

38·

Якщо число не парне, то менше парне множимо на 15 і добавляємо 15: 3

1715=16.

Використовуючи дію множення на 15 розглянемо множення на 16.

1416=14

1916=19

Використовуючи дію множення на 15 розглянемо множення на 14.

1714=17

1814=18

9. Способи множення на 25

Щоб число помножити на 25, потрібно його помножити на 100 та поділити на 4. Розглянемо множення чисел 64

Та можна дію ділення на 4 розбити на дію ділення двічі на 2

Розглянемо добуток 348·25 = (348 · 100) : 4 = (34800 : 2) : 2 = 17400 : 2 = 8700

Можна скористатися і таким способом, якщо дане число не кратне 4, Щоб число помножити на 25, потрібно поділити його на 4, тоді остачу множимо на 25 і дописуємо до результату.

Розглянемо добуток 66

Як наслідком з способу множення на 25, є множення на 26, тобто множимо на 25 і до результату додаємо саме число.

14= 350+14 = 364.

А також множення на 24, тобто множимо на 25 і від результату віднімаємо саме число. 1424 = 1425 –14 = 350 – 14 = 336.

10. Множення двозначних чисел, що закінчуються цифрою 5

Щоб помножити числа, запис яких закінчується цифрою 5 потрібно:

Помножити десяток першого числа та на 1 більший десяток другого числа.
Множимо одиниці цих чисел.
По черзі записуємо добутки.

Розглянемо добуток 75·25.

Оскільки 7·3 (на 1 більше ніж десяток другого числа) =21 і 5·5=25, тоді 75·25=2125.

Отжеусний рахунок відкриває широкі можливості для розвитку творчої ініціативи учнів. Усний рахунок сприяє тренуванню пам’яті, допомагає математичному розвитку логічного мислення. В усних обчисленнях немає головного шаблону і прийоми обчислень дуже різноманітні, що також сприяє розвитку людини.

Під час усних обчислень розвиваються такі якості людини, як уважність, зосередженість, витримка, кмітливість, самостійність.

Використання усних обчислень є засобом підвищення інтересу до предмету; засобом розвитку мислення, уваги, пам’яті; засобом розвитку кмітливості, активності, цілеспрямованості при розв’язанні поставлених завдань.

В побуті, на фабриці, на заводі, на ринку приходиться виконувати ті чи інші розрахунки, що також сприяє розвитку людини.

Дійсно, існують спеціальні способи виконання дій, які дозволяють звести обчислення до усних, швидким, що не вимагають унікальних здібностей, розрахованих на розум «звичайної» людини.

Головне – систематично тренуватися.

Література

Вукіна Н. В. Критичне мислення: як цьому навчати : наук.-метод. посібник / Н. В. Вукіна, Н. П. Дементієвська, І. М. Сущенко ; за наук. ред. О. І. Пометун. – Харків, 2007. – 190 с.
Пометун О. І. Основи критичного мислення : навчальний посібник для учнів старших класів загальноосвітньої школи / О. І. Пометун, Л. М. Пилипчатіна, І. М. Сущенко, І. О. Баранова. – Тернопіль : Навчальна книга – Богдан, 2010. – 216 с.
Салтановська Н. І, Моспанок В. О. Прийоми усних обчислень як засіб розвитку особистості учня основної школи / Сучасні інформаційні технології та інноваційні методики у підготовці фахівців: методологія, теорія, досвід, проблеми. – Вінниця, 2012 р., С. 134-139

1.12. ФОРМУВАННЯ КРИТИЧНОГО МИСЛЕННЯ ШКОЛЯРІВ НА УРОКАХМАТЕМАТИКИ З ВИКОРИСТАННЯМ ГЕОМЕТРІЇ ЯК ЗАСІБ ПІДВИЩЕННЯ МАТЕМАТИЧНИХ ЗНАНЬ

Стрімке зростання обсягу інформації, розвиток комп’ютерних технологій вимагає пошуку та впровадження нових методів і прийомів у методиці навчання математики. Виходячи з Державної національної програми «Освіта», закону України «Про освіту» та Державного стандарту, основною метою освітньої галузі «Математика» є формування в учнів математичної компетентності; розвиток здатності чітко та аргументовано формулювати і висловлювати свої судження; забезпечення інтелектуального розвитку учнів. Сучасному суспільству потрібна творча й активна особистість.

Початок XXI століття означений складним пошуком нового світорозуміння, педагогічного світовідчуття у всьому світі. За умов змін в українському суспільстві особливого значення набувають питання формування нових життєвих стратегій, компетентності, конкурентоспроможності, посилення гнучкості та мобільності соціальної поведінки молодої людини. За таких умов як ніколи гостро стоїть завдання створення нової філософії освіти, відкритої до прагнень та розвитку життєвого потенціалу людини. На цій основі формується нова педагогіка - педагогіка компетентної людини. Більшість педагогів погоджується з фактом, що якість системи середньої освіти визначається тим, наскільки підготовлені до життя випускники школи, що знання, вміння і навички, яких набувають учні у процесі вивчення шкільних предметів, не переходять автоматично в таку готовність. Саме компетентний підхід покликаний подолати прірву між освітою і потребами життя.

Наразі надзвичайно важливо сприяти виробленню у підлітків уміння критично мислити, об’єктивно оцінювати різноманітні явища, процеси, події. Тому вагомість формування критичного мислення особистості зумовлена ще й тим, що притаманна нашому часу динаміка технологічного і соціального прогресу вимагає від людини умінь швидко адаптуватися, змінюватися і вдосконалюватися на основі самостійного набуття знань, знаходити шляхи розв’язання завдань, які виникають у будьяких нестандартних ситуаціях, пошуку внутрішнього потенціалу з метою гармонійної адаптації в полікультурному світі [2].

Дослідженню критичного мислення присвячено праці багатьох науковців. Цей феномен у своїх наукових працях досліджували Дж. Брунер, Л. Виготський, Д. Дьюї, Д. Клустер, А. Кроуфорд, М. Ліпман, Д. Макінстер, С. Метьюз, Р. Пауль, Ж. Піаже, Д. Халперн та інші науковці. Серед українських учених вивченню цього питання приділяють значну увагу І. Бондарчук, Т. Воропай, О. Пометун, С. Терно, О. Тягло, Л. Терлецька та інші. Ідея розвитку критичного мислення для української дидактики і методики навчання є достатньо новою. В Україні інтерес до розвитку критичного мислення як освітньої інновації з’явився наприкінці XX століття. Так, у 1996 році український учений О. Тягло акцентував увагу на важливості і значущості розвитку критичного мислення в умовах інформаційного суспільства. Сьогодні очевидно, що критичне мислення означає не негативність суджень або критику, а розумний розгляд різноманітності підходів для винесення обґрунтованих суджень і рішень. Тому, на думку відомого американського психолога Д. Халперн, освіта, розрахована на перспективу, має забезпечити формування в учнів двох основних груп умінь: умінь швидко орієнтуватись у зростаючому потоці інформації та знаходити потрібне і вмінь осмислювати та застосувати здобуту інформацію [1].

Розглянемо декілька методів, які можна використати на уроці математики для формування математичних знань. Метод «Кошик ідей» - його ціллю є здебільшого зацікавлення дітей. Вчитель задає питання про те, що учні знають про певну тему або проблему. Кожен учень записує те, що згадає з цієї теми (на це виділяється 2 хвилини). Далі учні обмінюються інформацією в командах, записують нові ідеї. Потім по колу кожна команда називає якийсь із записаних фактів і всі разом складають єдиний список ідей у вигляді тез в один «кошик». Наприкінці заняття вчитель може виправити недостовірні тези і вписати туди разом з дітьми нову правдиву інформацію.

Метод «Інсерт» (інтерактивна система запису для ефективного читання і розмірковування) дає можливість дитині глибше осмислити запропонований для опрацювання текст. Учні читають текст і ставлять відповідні позначки біля окремих слів або фраз: «+Я це знав»; «- Я це не знав»; «? Це мене здивувало»; «! Я хотів би дізнатися про це детальніше». Далі учні заповнюють таблицю, куди вписують фрази, слова або речення у відповідні колонки.

«Кути» – метод навчання використовується, щоб навчити дітей самовизначенню або відстоюванню своєї точки зори. Даний метод рекомендуємо використовувати при розв’язувані задач на дослідження або доведення. Назву засіб отримав від форми її проведення – учні формулюють різні точки зору щодо теми та розходяться по різних «кутах», щоб знайти відповідні аргументи. Вчителю потрібно так організувати процес, щоб учні самостійно визначили спірні питання та напрям дискусії.

Ми розглянули тільки три методи, але їх існує набагато більше і для вивчення кожної теми уроку можна підібрати свій метод або технологію навчання. Деякі з них доцільно використовувати на етапі пояснення нового матеріалу, інші при формуванні вмінь та навичок, існують технології навчання, які можна використовувати під час закріплення вже вивченого матеріалу.

На жаль, у системі сучасної педагогічної освіти майбутні педагоги не отримують поки що ані цих знань, ані цих умінь. Тож сьогодні слід включити таку підготовку в систему професійного розвитку і вчителів, і викладачів вищої педагогічної школи, а ще зорієнтувати неформальну тренінгову освіту педагогів у напрямі розвитку критичного мислення.

З’ясовано, що мислення є складним психологічним і соціально-історичним феноменом, предметом комплексних, міждисциплінарних досліджень. Воно розглядається як процес пізнавальної діяльності індивіда, що характеризується узагальненим і опосередкованим відбиттям дійсності. Інтерес до розвитку критичного мислення як освітньої технології з’явився в Україні близько десяти років потому. Таким чином, визначення критичного мислення відбулося через перелік його ознак і показників, які було об’єднано в мотиваційно-ціннісний, інтелектуальний та творчий компоненти критичного мислення, що слугували в подальшому критеріями його розвитку.

Література

Бондарук І. П. Формування критичного мислення дев’ятикласників у процесі навчання історії/І. П. Бондарук. – К, 2012. – 276 с.
Чаплак Я. Роль критичного мислення у творчих пошуках «внутрішнього камертону душі» особистості [Електронний ресурс] / Я. Чаплак, М. Марчук // № 4. – 2011. – Режим доступу до ресурсу:
http://web.snauka.ru/issues/2011/08/1516

РОЗДІЛ 2. ІННОВАЦІЙНІ ТЕХНОЛОГІЇ ЯК ЗАСІБ РОЗВИТКУ

КРИТИЧНОГО МИСЛЕННЯ УЧНІВ НА УРОКАХ МАТЕМАТИКИ

2.1 МАТЕМАТИЧНІ КОМП’ЮТЕРНІ ІГРИ ЯК ЗАСІБ РОЗВИТКУ

КРИТИЧНОГО МИСЛЕННЯ УЧНІВ

Нині перед українською школою постає завдання виховати особистість, яка здатна самостійно мислити, приймати сміливі, нестандартні рішення, породжувати оригінальні ідеї. Головне завдання вчителів при цьому сформувати в учнів вміння виділяти головне, аналізувати, систематизувати інформацію, робити висновки, тобто розвивати критичне мислення.

На даний час не існує єдиного підходу до визначення поняття «критичне мислення учнів». Проблему розвитку критичного мислення досліджували ряд закордонних вчених: Дж. Брунер, А. Кроуфорд, Л. Виготський, Д. Дьюї, С. Метьюз, М. Ліпман, Д. Макінстер, Р. Пауль, Ж. Піаже, Д.Халперн та ін. Серед українських науковців вивченню цього поняття присвячені праці І. Бондарчук, О. Пометун, О. Тягло, Т. Воропай, Л. Терлецької, С.Терно та інших.

Нам імпонує наступний підхід С.Терно, за яким критичне мислення - це здатність особистості використовувати певні прийоми обробки інформації, що дозволяють отримати бажаний результат. До основних рис критичного мислення вчений відносить такі уміння: 1) робити логічні умовиводи; 2) ухвалювати обґрунтовані рішення; 3) давати (оцінку позитивних та негативних рис) як отриманої інформації, так і самого розумового процесу; 4) спрямованість на результат. На нашу думку, одним із засобів розвитку критичного мислення є комп’ютерні дидактичні ігри [2].

Навчання на основі гри мотивує учнів приймати самостійні рішення, розвиває увагу та сконцентрованість, вміння застосовувати теоретичні знання при розв’язуванні завдань практичного змісту, тривалий час виконувати певні дії. Крім того, навчальні комп’ютерні ігри дозволяють усунути одну з найважливіших причин негативного ставлення дітей до навчання – проблеми нерозуміння матеріалу і психологічного дискомфорту. Правильно організована ігрова діяльність дозволяє розвивати самостійність і кмітливість учнів на уроках математики.

Комп’ютерні ігри, залежно від мети та типу уроку, можна використовувати на всіх етапах навчання: ознайомлення з новим матеріалом, закріплення, повторення, контроль знань та вмінь.

Нині існує ряд розробок комп’ютерних дидактичних ігор, зокрема, Learning.ua, mathplayground, Heroes of Math and Magic, vsi_predmety_plus1s, Bristar, Matific та ін.

Зупинимось детальніше на характеристиці Matific – сайт з математичними іграми, що містить багато різноманітних задач з математики для дошкільнят та учнів 1-4 класів, розв’язування яких може сприяти розвитку критичного мислення. До кожної теми пропонується велика кількість математичних ігор.

Розглянемо деякі із запропонованих на сайті Matific ігор для учнів 4-го класу:

«Чудо магазин». Гра зводиться до додавання десяткових дробів. Таким чином будь-яке теоретичне завдання стає зрозумілим на практиці, також учні аналізують кожне завдання і бачать практичну необхідність математичних знань.
- Дану гру можна застосовувати при вивченні десяткових дробів під час закріплення знань.
«Вгадай розгортку». Завдання гри – учням потрібно обрати правильну розгортку представленого паралелепіпеда або куба. Такі завдання розвивають уяву та просторове мислення

Можна використовувати на уроці закріплення знань.
«Розв’яжи будь-яким способом»: учням потрібно визначити середнє значення
- Дану вправу можна використовувати на уроці закріплення матеріалу, під час вивчення теми «Середнє арифметичне. Середнє значення величини».
«Переливання» – це головоломка, яка гарно розвиває логічне мислення та кмітливість, суть гри полягає в тому, що учням пропонується дві склянки води з певною місткістю і їх завдання набрати кількість води, яка вказана в умові задачі (рис.4)

Рис. 4

Отже, систематичне використання комп’ютерних ігор на уроках математики – це не примха, а вимога сьогодення. Методично грамотно побудовані уроки з використанням математичних комп’ютерних ігор не лише розширюють і закріплюють отримані знання, а й значно підвищують творчий потенціал учнів, розвивають самостійне, критичне мислення, формують ініціативну особистість.

Література

Інтенсивні вправи на взаємодію для учнів [Електронний ресурс] – Режим доступу до ресурсу: https://www.matific.com .
Терно С. О. Критичне мислення – сучасний вимір суспільствознавчої освіти/С. О. Терно. – Запоріжжя: Просвіта, 2009. – 268 с.

2.2. РОЗВИТОК КРИТИЧНОГО МИСЛЕННЯ УЧНІВ НА УРОКАХ МАТЕМАТИКИ З ВИКОРИСТАННЯМ ЕЛЕКТРОННИХ ЗАСОБІВ НАВЧАННЯ

На сьогоднішній день концепцією навчання в Україні передбачено високий загальноосвітній та культурний рівень підготовки учнів, які мають одержати не лише різнобічні глибокі та міцні знання основ наук, але й уміння творчо їх застосовувати, постійно поповнюючи. Суспільство занадто швидко змінюється в розвитку, йому потрібні нові підходи у формуванні творчої особистості, людини, здатної вчасно й правильно розв'язувати проблеми, досягати поставленої мети. У великій мірі цього досягають завдяки урокам математики, адже заняття з математики – це оволодіння образного сприйняття світу. Воно змушує працювати уяву, фантазію, розвиває пізнавальні, творчі здібності, формує особистість. На уроках математики наше завдання – не нагромаджувати знання, а вести учнів по дорозі пошуку, спрямувавши їх на формування вмінь і навичок, щодо орієнтування в інформаційному просторі.

Учням подобаються ті види навчальної діяльності, що не тільки надають їм матеріал для роздумів, можливість проявляти ініціативу та самостійність, але й потребують розумового напруження, винахідливості та творчості. Якщо ви заздалегідь підготуєте завдання на картках для сильніших учнів, щоб вони, швидко розв’язавши задачу чи приклад, не нудьгували, то у вас на уроці буде 100 % активність, усі учасники процесу отримають задоволення не тільки від нього самого, а й від своєї участі в ньому [1].

Розвиток критичного мислення – це на сьогодні дуже важливий елемент не лише у навчанні математики, а й в повсякденному житті, коли неможливо діяти без постійного пристосування до нових політичних, економічних обставин, без ефективного вирішення проблем, значну частину яких неможливо передбачити. Саме тому очевидна життєва необхідність критичного мислення для української освітньої системи [2].

У навчальних закладах України було апробовано ряд технологій спрямованих на розвиток особистісних якостей у дитини, серед них провідну роль зайняло критичне мислення.

Що ж взагалі воно таке, це критичне мислення? На мою думку, це пошук здорового глузду – як міркувати об'єктивно і діяти логічно з урахуванням як своєї точки зору, так й інших думок, уміння відмовитися під тиском логіки від власних упереджень.

Критичне мислення формується в проблемній ситуації, це своєрідна перевірка запропонованих рішень з метою визначення галузі їх можливого застосування. Воно важливе як інструмент для дослідження. Щоб ваші учні на уроках математики могли мислити чітко, логічно, швидко, намагайтеся з перших уроків привчати їх до:

Готовності до планування. Оскільки думки виникають хаотично, важливо їх упорядкувати, вирішити, що за чим використати. Висловлюючись мовою математики, написати (запланувати) алгоритм дії.
Гнучкості. Якщо учень не сприймає ідей інших, він ніколи не продукуватиме їх сам. Спочатку треба зібрати інформацію, обдумати і тільки тоді приймати рішення. Висловлюючись мовою математики, це звучить приблизно так: якщо, то.
Наполегливості. Якщо завдання не виходить розв’язати, то, як правило, учні його ігнорують, або списують як не в друзів, то в ГДЗ. Тому, працюючи разом з батьками, шукайте причину неправильного розв’язку, розв'яжіть ще кілька тотожних завдань, щоб уникнути типових помилок [2].

Зараз на уроці вчитель повинен бути готовим до будь-яких несподіванок, керуючись розробленою системою уроків. А ще в якісній підготовці до уроку допоможуть інформаційно-комунікаційні технології (ІКТ), які можна сміливо використовувати на уроках математики.

При застосуванні ІКТ реалізуються основні принципи активізації пізнавальної діяльності, на 1,5 % підвищується обсяг виконуваної роботи, збільшується зміна видів навчальної діяльності. За рахунок цього в учня формується позитивна мотивація засвоєння знань, розвивається асоціативне, критичне мислення, удосконалюються математичні, конструкторські та комбінаторні здібності, пам'ять, просторова уява, увага, моторика, створюється гарний настрій.

Наприклад, для показу презентацій потрібна програма POWER POINT, що зекономить час на уроці, дасть змогу створити емоційне ставлення до навчальної інформації, ну і, звичайно, підвищити ступінь наочності. Якщо ви в досконалості володієте текстовим редактором WORD, підготуйте картки із завданнями, а EXCEL та FNGraph допоможуть побудувати графіки функцій, зобразити геометричні фігури.

Для перевірки засвоєного матеріалу можна провести комп'ютерне тестування. Тут у нагоді стануть такі програми, як TestW та My Test. Застосовуючи ці засоби на уроках математики ви отримаєте нові форми комутативної роботи учнів, чим підвищите результативність навчального процесу, виховаєте особистість, яка буде комфортно себе відчувати в інформаційному суспільстві. Не забуваймо також і про нові джерела інформації – наприклад, мережу Інтернет [3].

На сьогодні з'явилось багато сайтів, де зібрано теоретичний матеріал, а також в мережі он-лайн можна переглянути практичне розв'язування тих чи інших завдань. А ще в запасі у вчителя є так звані ППЗ (педагогічні програмні засоби), ̶ це так звані засоби комп'ютерної підтримки вивчення різних розділів шкільного курсу математики.

На будь-якому уроці необхідно, як ви знаєте, проводити фізкультурні хвилинки. Варто створити так званий фотошоп, де в цікавому форматі зобразити геометричні фігури, видатних математиків, яких учням необхідно буде розгадати. В результаті отримаємосвоєрідний квест, що сприяє розвитку пам'яті, уяви, а також критичного мислення.

Підводячи підсумок вище викладеного, можна сказати, що критичне мислення – це:

уміння урівноважувати у своїй свідомості різні точки зору;
уміння аналізувати;
об'єднання активного й інтерактивного процесу;
перевірка окремих ідей та можливість їх застосування.

Саме на уроках математики сучасний комп'ютер може стати для учня рівноправним партнером, що здатний швидше за вчителя зреагувати на всі його дії й запити.

Література

Горошко Ю. В. Вплив нової інформаційної технології на практичну значимість результатів навчання математики: Автореф. дис. канд. пед. наук: спец. 13.00.02/ Ю. В. Горошко – К.,1992. – 22 с.
Селевко Г. К. Сучасні педагогічні технології: Навчальний посібник/ Г. К. Селевко – М.: Народна освіта, 1998. – 258 с.
Сучасний урок. Інтерактивні технології навчання: Наук.-метод. посібн./О. І. Пометун, Л. В. Пироженко. За ред. О. І. Пометун – К.: А.С.К. 2004,

– 192с.

2.3. ВИКОРИСТАННЯ СУЧАСНИХ ПРОГРАМНИХ ЗАСОБІВ НА УРОКАХ МАТЕМАТИКИ

На сучасному етапі розвитку суспільства мета освіти полягає в тому, щоб підготувати конкурентоспроможну особистість, яка користується попитом на ринку праці, розвинути у школярів потребу в саморозвитку, самовдосконаленні. Слід зазначити, що і самі школярі виявляють зацікавленість в оволодінні знаннями, вміннями і навичками. Безсумнівно, в основі методів, використовуваних вчителем в навчально-виховному процесі, лежить уміння самостійно конструювати знання, уміння орієнтуватися в інформаційному просторі, розвиток пізнавальних, творчих навичок учнів, розвиток критичного мислення [5].

Тому постає необхідність оновлення змісту навчання, розробки нових методичних і дидактичних засобів навчання, за допомогою яких у учнів виникає пізнавальний інтерес, мотивація до подальшої роботи. Це можливо здійснити з використанням інноваційних технологій.

Критичне мислення - це спосіб здобувати знання, вміння аналізувати, оцінювати, виносити обґрунтовані судження, виробляти власну думку з досліджуваної проблеми і вміння застосовувати знання, як в стандартній, так і нестандартній ситуації [6].

Сама технологія розвитку критичного мислення передбачає три етапи конструктивно-смислової побудови уроку: виклик, реалізація, рефлексія. Тому постає завдання розглянути програмні засоби, які може використовувати вчитель, щоб зробити урок насиченішим та яскравішим на кожному етапі. Адже застосування сучасних програмних засобів на уроках робить його нетрадиційним, цікавим, дає змогу використовувати різні варіанти подачі навчального матеріалу і різні підходи в навчанні.

Виклик. Цей етап можливий з використанням слайдів з текстовими, графічними та відео зображеннями. Застосування художніх тематичних фільмів дозволяє побачити проблему візуально, краще зрозуміти її і зробити об'єктивні висновки, які стануть основою для формування альтернативних підходів для вирішення конкретної проблеми або прийняття певного рішення по певній ситуації. Це підвищує інтерес до процесу навчання і активного сприйняття навчального матеріалу, сприяє кращому засвоєнню нової інформації.
Реалізація сенсу. Використовуються мультимедійні презентації, електронні підручники, електронні навчально-методичні посібники, електронні енциклопедії. Такі завдання розвивають гнучкість мислення, вміння мислити самостійно та застосовувати теорію на практиці.
Рефлексія. Часто виникає питання про механізм діагностики результативності процесу навчання. Тому на цьому етапі викладач оцінює результат роботи студентів. Ефективним способом буде використання тестових і автоматизованих систем контролю [6].

На кожному етапі розвитку критичного мислення Вам можуть допомогти різні сервіси та веб-ресурси, які створенні спеціально для вчителів і містять в собі найрізноманітніші функції.

Серед них можна виділити:

Інтерактивна онлайн-дошка classroomscreen. Просте онлайн-середовище для інтерактивних дошок, яке є безкоштовним та не потребує реєстрації. Тут Ви можете писати, малювати, виставляти час і таймер, вказувати команди за допомогою яких можна керувати діяльністю учнів. Також наявна функція «світлофор», який можна використовувати під час самостійних завдань (наприклад, коли потрібно здавати роботу вмикати зелений колір). Також є вибір випадкового імені, який можна використовувати під час опитувань, мозкового штурму, тощо [4] .
Сервіс ZooBurst. За допомогою цього сервісу можна створювати цікаві інтерактивні 3D-книги. Працювати з сервісом нескладно, особливо якщо це робити в браузері Google Chrome. У книгу можна вставляти картинки, текст, посилання на інтернет ресурси. Великі можливості має і фонове розширення книги: зміна кольору, вставка фонових малюнків. При перегляді книги можна перегортати її в тривимірному просторі, що створює додатковий ефект і привабливість, особливо для молодших школярів. Єдиний недолік - можна створити всього 10 сторінок книги і тільки 10 книг (в безкоштовному акаунті), в платному - книги до 50 сторінок і кількість необмежена [1].
Інтернет-інструмент оцінювання учнів. Учитель може створювати свої тести, редагувати їх. Учень, користуючись комп'ютером, ноутбуком або смартфоном вводить ПІН-код і своє ім'я, тобто тести можуть бути відтворені на будь-якому пристрої з доступом до Інтернету. Всі учні отримують однакові завдання, але кожен з учнів на своєму пристрої отримає випадкову послідовність питань і буде працювати з тестом у нормальному для себе темпі. Після кожного тестування вчитель не тільки ознайомлюється з результатами, але і має можливість одержувати дані в таблиці Excel. При бажанні вчитель може скористатися не тільки своїми тестами, але й використовувати готові, розміщені в бібліотеці Quizizz, яких там викладено чимало на будь-які теми [3].
Отже ці програмні засоби, які можуть допомогти розвивати критичне мислення учнів на різних етапах уроку. Описані переваги та недоліки застосування, особливості та деталі при використовувані цих програмних засобів.

Література

Gynzy heeft in de digitale verwerking Werelden voor rekenen, spelling, grammatica en woordenschat [Електроннийресурс] – Режимдоступудоресурсу: https://api.gynzy.com/en/.
ZooBurst is a service for creating 3D books. [Електронний ресурс] – Режим доступу до ресурсу: https://zooburst -ios.soft112.com/
Quizizz -Free gamified quizzes for every subject to play in class. [Електронний ресурс] – Режим доступу до ресурсу: https://quizizz.com .
Інтерактивна онлайн-дошка classroomscreen [Електронний ресурс] – Режим доступу до ресурсу: https://www.classroomscreen.com
Начаева Е. С. Возможности применения ИКТ при использовании технологии критического мышления [Електронний ресурс] / Е. С. Начаева// Интернет-журнал "Просвещение". – 2015. – Режим доступу до ресурсу: http://old.prosveshenie.kz/882 -vozmozhnosti -primeneniya -ikt -pri -ispolzovanii tehnologii -kriticheskogo -myshleniya.html
Терно С. О. Теорія розвитку критичного мислення (на прикладі навчання історії)/С. О. Терно : [посібник для вчителя]. – Запоріжжя: Запорізький національний університет, 2011. – 105 с.

ДОДАТОК 1

Тема уроку. Досліджуємо число і цифру 5 . Склад числа 5

Мета:формувати поняття число і цифра 5, обчислювальні навички; дослідити склад числа 5

Дидактична задача: ознайомити з числом і цифрою 5 та складом числа 5, закріпити означення арифметичної дії додавання, вчити користуватися ним під час знаходження значень виразів на основі складу числа; формувати вміння складати вираз за малюнком, предметами; здійснювати підготовчу роботу до збільшення числа на кілька одиниць.

Розвивальна задача: вчити будувати міркування шляхом виконання завдань в нестандартній обстановці.

Хід уроку

І. Мотивація навчально-пізнавальної діяльності учнів

Ви вже навчилися міркувати при додаванні чисел 2,3,4.Мабуть, ви вже готові до складання складу числа 5. Після того як ми дослідимо склад числа 5 ви будете дуже швидко, а головне- правильно додавати числа в межах 5. Якщо хтось ще має труднощі з цим, треба обов’язково додатково попрацювати. Отже, сьогодні ми дослідимо склад числа 5, розкриємо «секрет» числа і цифри 5. Тому будьте уважні, щоб зробити правильні висновки.

II.Актуалізація опорних знань

Діти вишикувані в шеренгу в спортивному залі згідно зросту. Даються такі команди:

- по порядку розрахуйсь;

-на перший-десятий розрахуйсь;(діти діляться на дві команди по 10 чоловік у кожній)

Перші десять учнів тримають пусті пазли без цифр в хаотичному порядку. Інші десять учнів тримають цифри від 0 до 10 в хаотичному порядку.

$C:\Users\usserweerty\Desktop\Новая папка\DSC_1087.JPG$

За командою вчителя діти знаходять свою пару (пазл+ цифра). Далі дається команда утворити ряд натуральних цифр від нуля до десяти. Після чого перші десять учнів, які тримають пазли повертаються спиною до інших учнів. Далі вчитель називає цифру , учень з цією цифрою повертається обличчям, а інші учні повинні назвати сусідів цього числа. Після цього перевіряється правильність відповіді, і аналогічно повторюється сусіди чисел.

$C:\Users\usserweerty\Desktop\Новая папка\DSC_1092.JPG$

$C:\Users\usserweerty\Desktop\Новая папка\DSC_1093.JPG$

$C:\Users\usserweerty\Desktop\Новая папка\DSC_1094.JPG$

ІІІ. Формування нових знань і способів дій

Діти знову шикуються в одну шеренгу, після команди вчителя діти розраховуються на 1-5 і утворюються групи по 5 дітей у кожній. За командою вчителя всі учні присідають, тоді в першій групі встає один з учнів, інші чотири- сидять. В наступній групі два учні стоять, а три –сидять. Ще в наступній три-стоїть, а два-сидить. В наступній чотири- стоять, а один-сидить. Відповідно до цього кожна група складає свій приклад(1+4=5;2+3=5;3+2=5;4+1=5). Після того, як кожна з груп повторить свій приклад, тоді доходять до висновку, що відповідь однакова- 5. Для закріплення складу числа 5 в кожну групу даються предмети за допомогою яких учні можуть скласти приклад, де відповіддю буде число 5.

Наприклад:

1група-всі п’ять різних предметів;

2група- один куб і чотири конуса;

3група- два м’ячика і три палички і т.д.

$C:\Users\usserweerty\Desktop\Новая папка\DSC_1083.JPG$

ІV.Закріплення вивченого. Формування вмінь і навичок

Після цього діти йдуть до класу, де сідають у свої робочі групи, їм потрібно скласти цифру 5. Далі із запропонованих малюнків( м’ячики, пінгвіни, ромашки) вирізати лише ті предмети, яких 5.

$C:\Users\usserweerty\Desktop\Новая папка\DSC_1068.JPG$

$C:\Users\usserweerty\Desktop\Новая папка\DSC_1076.JPG$

$C:\Users\usserweerty\Desktop\Новая папка\DSC_1077.JPG$

На закріплення знань діти ще раз повторюють склад числа 5

$C:\Users\usserweerty\Desktop\Новая папка\DSC_1067.JPG$

V. Рефлексія навчально-пізнавальної діяльності учнів

Що на уроці було для вас новим? Що важливе ви повторили? Які вміння покращили?

Додаток 2

Тема. Досліджуємо число і цифру 7. Склад числа 7.

Мета: формувати поняття число і цифра 7, обчислювальні навички; дослідити склад числа

Дидактична задача: ознайомити з числом і цифрою 7 та складом числа 7, закріпити означення арифметичної дії додавання, 7 познайомити з написанням цифри 7, пояснити утворення числа 7 додаванням 1 до попереднього числа, навчити писати цифру 7, вправляти дітей в лічбі предметів у межах 7, в порівнянні чисел у межах 7, узагальнити вміння записувати і розв’язувати приклади на додавання; знання про попереднє і наступне числа;

Розвивальна задача: вчити будувати міркування шляхом виконання завдань в нестандартній обстановці; розвивати мислення, розвивати загально-навчальні уміння і навички: мовлення, увагу, пам’ять, мислення; інтерес до предмета; виховувати якості, необхідні дітям для успішного навчання.

Методи і прийоми: діяльнісний метод навчання, створення проблемної ситуації, пошук рішення, наочно – ілюстративний, словесний, репродуктивний.

Хід уроку

І. Мотивація навчально-пізнавальної діяльності учнів

Ви вже навчилися міркувати при додаванні чисел 2,3,4,5,6Мабуть, ви вже готові до складання складу числа 7. Після того як ми дослідимо склад числа 7 ви будете дуже швидко, а головне- правильно додавати числа в межах 7. Якщо хтось ще має труднощі з цим, треба обов’язково додатково попрацювати. Отже, сьогодні ми дослідимо склад числа 7, розкриємо «секрет» числа і цифри 7. Тому будьте уважні, щоб зробити правильні висновки.

Аутотренінг

А тепер давайте проведемо автотренінг і налаштуємося на урок.

Я – учень.

Я все розумію.

Я все буду знати.

Вправа «мікрофон»

Подумайте і скажіть, яким має бути наш урок.

(цікавим, навчальним, казковим, веселим, світлим, загадковим, проблемним)

А учні на уроці якими повинні бути?

(дисциплінованими, уважними, зібраними, активними, вправними)

Отже, якщо ви будете такими, то ми разом створимо цікавий, творчий, продуктивний урок. А він у нас сьогодні дійсно незвичайний.
А працюватимемо під гаслом:

Щоб робота в нас кипіла,

Працювати будем:

Швидко! Дружно! Вміло!

II.Актуалізація опорних знань

1.Рахунок

Рахунок від 1 до 10 (плескаємо в долоні вгорі)

Рахунок від 10 до 1(стоячи, плекаємо в долоні внизу)

Порахувати до 20 ланцюжком (1- парта – один, 2-парта – два, …)

Рахунок двійками

2. Гра «Мовчанка»

Молодці. Мовчун говорити не вміє. Отже, всі відповіді потрібно показати за допомогою математичних віял.

Яке число передує числу 4? (3)
Яке число наступне за числом 5? (6)
Яке число стоїть між числами 2 і 4? (3)
Увага! Віяла покласти. А тепер дайте відповідь за допомогою піднятої руки.
Назвати сусідів числа 6. (5 та 7)

3.Графічний диктант

$C:\Users\usserweerty\Desktop\Мамині файли\Фотки мама школа\DSC01330.JPG$ $C:\Users\usserweerty\Desktop\Мамині файли\Фотки мама школа\DSC01336.JPG$

ІІІ. Формування нових знань і способів дій

Утворення числа 7

Задача – вірш

Шість метеликів літають

І на квіточки сідають.

Прилетів іще один,

Сів на квіточку і він.

Полічімо швидше всіх –

Цих метеликів прудких.

Скільки метеликів було спочатку? (6 метеликів)

Скільки метеликів прилетіло? (Один)
Як дізнатися скільки стало всіх метеликів? (Дією додавання)
Складіть вираз.
Скажіть рівність.
Як утворилося число 7? (До 6 додали 1 – одержали 7 метеликів)
Що показує число 6? (Кількість метеликів, які літали)
Що показує число 1? (Кількість метеликів, які прилетіли)
Що показує число 7? (Кількість метеликів всього)

Знайомство із цифрою 7

- на що схожа цифра сім?

Написання цифри 7

Цифра 7 складається з трьох елементів: хвилястої горизонтальної лінії, довгої прямої похилої лінії та короткої горизонтальної лінії.
Пропишіть цифру сім в повітрі.
Пропишіть ніжкою по полу
Пропишіть язичком в роті.

Де в нашому житті зустрічаємо число 7?

Сім кольорів веселки –

Відомо нам усім.

Є сім веселих ноток.

$C:\Users\usserweerty\Desktop\DSC_0309.JPG$ У тижні днів теж сім.

викладіть цифру з різного матеріалу.

4.Досліджуємо склад числа 7

- діти за допомогою різних предметів викладають склад числа 7

Наприклад:

-учні складають вираз до 1+6=7

2+5=7 і т.д.

ІV.Закріплення вивченого. Формування вмінь і навичок

Далі діти розташовуються на килимку.

Їм пропонується розрізаний чайник на частинки ( носик, ручка, кришка, ) а в середині записані різні вирази на склад числа 5,6,7.

знайти відповідний вираз або цифру, щоб відповідь була однакова

$C:\Users\usserweerty\Desktop\DSC_0306.JPG$

$C:\Users\usserweerty\Desktop\DSC_0305.JPG$

після чого діти знову повторюють склад числа 7

ІV. Рефлексія

Якому числу був присвячений урок?(утворення числа 7)
А що ви дізналися?
З яким настроєм ви закінчуєте урок? Які вміння покращили?
Ви сьогодні добре попрацювали, скажемо один одному СПАСИБІ.

docx

Завантажити

Зберегти на потім

Додав(-ла)

Бабич Людмила Іванівна

Пов’язані теми

Математика, 1 клас, Розробки уроків

НУШ

Додано

12 грудня 2021

Переглядів

3578

Оцінка розробки

Відгуки відсутні

Розвиток критичного мислення

РОЗДІЛ 1. ФОРМУВАННЯ І РОЗВИТОК КРИТИЧНОГО МИСЛЕННЯ УЧНІВ

4

1.1.ПРИЙОМИ ТА СТРУКТУРА РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ НАУРОКАХ МАТЕМАТИКИ

4

1.2.КЛАСТЕР, ЯК ОДИН ІЗ МЕТОДІВ РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ

8

1.3.РОЗВИТОК КРИТИЧНОГО МИСЛЕННЯ УЧНІВ НА УРОКАХ МАТЕМАТИКИ НА ЕТАПІ РЕФЛЕКСІЇ

11

1.4.МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ ЯК ЗАСІБ РОЗВИТКУ

КРИТИЧНОГОМИСЛЕННЯ УЧНІВ

14

1.5.ЗАСТОСУВАННЯ ПРИЙОМІВ ІНТЕРАКТИВНОГО НАВЧАННЯ ЯК ЗАСОБУ РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ УЧНІВ НА УРОКАХ МАТЕМАТИКИ

17

19

22

25

27

30

33

1.12.ФОРМУВАННЯ КРИТИЧНОГО МИСЛЕННЯ ШКОЛЯРІВ НА

УРОКАХ МАТЕМАТИКИ З ВИКОРИСТАННЯМ ГЕОМЕТРІЇ ЯК

ЗАСІБ ПІДВИЩЕННЯ МАТЕМАТИЧНИХ ЗНАНЬ

40

РОЗДІЛ 2. ІННОВАЦІЙНІ ТЕХНОЛОГІЇ ЯК ЗАСІБ РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ УЧНІВ НА УРОКАХ МАТЕМАТИКИ

43

КРИТИЧНОГО МИСЛЕННЯ УЧНІВ

43

46

49

52

56

РОЗДІЛ 1. ФОРМУВАННЯ І

РОЗВИТОК КРИТИЧНОГО МИСЛЕННЯ УЧНІВ

1.1. ПРИЙОМИ ТА СТРУКТУРА РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ НА УРОКАХ МАТЕМАТИКИ

1.2. КЛАСТЕР, ЯК ОДИН ІЗ МЕТОДІВ РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ

1.3 РОЗВИТОК КРИТИЧНОГО МИСЛЕННЯ УЧНІВ НА УРОКАХ МАТЕМАТИКИ НА ЕТАПІ РЕФЛЕКСІЇ

1.4. МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ ЯК ЗАСІБ РОЗВИТКУ

КРИТИЧНОГОМИСЛЕННЯ УЧНІВ

1.5. ЗАСТОСУВАННЯ ПРИЙОМІВ ІНТЕРАКТИВНОГО НАВЧАННЯ ЯК

1.6. ФОРМУВАННЯ КРИТИЧНОГО МИСЛЕННЯ В ІНТЕГРОВАНОМУ КУРСІ ВИВЧЕННЯ МАТЕМАТИКИ

1.7. ТЕХНОЛОГІЇ РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ НА УРОКАХ МАТЕМАТИКИ

1.8. РОЗВИТОК КРИТИЧНОГО МИСЛЕННЯ УЧНІВ ПІД ЧАС РОЗВ’ЯЗУВАННЯ ТЕКСТОВИХ ЗАДАЧ НА УРОКАХ МАТЕМАТИКИ

1.9. ПРИЙОМИ ФОРМУВАННЯ КРИТИЧНОГО МИСЛЕННЯ УЧНІВ В ПРОЦЕСІ РОЗВ’ЯЗУВАННЯ ЗАДАЧ НА РУХ

1.10. ВИКОРИСТАННЯ ТЕХНОЛОГІЇ КРИТИЧНОГО МИСЛЕННЯ У

ПРОЦЕСІ ВИВЧЕННЯ ЧОТИРИКУТНИКІВ

1.11. РАЦІОНАЛЬНІ ОБЧИСЛЕННЯ ЯК ОДНА З ФОРМ ПРОЯВУ