Розвиток логічного мислення на уроках математики за допомогою нестандартних завдань

 

Зміст

 

Вступ ..................................................................................................................4

Розділ 1. Теоретичні аспекти проблеми розвитку логічного мислення учнів

 на уроках математики ………………………..................................................5                                                 

1.       Проблема розвитку мислення в процесі навчання……………..5
2.       Суть розвитку логічного мислення дітей середнього шкільного віку..………………………………………………………………..…7
3.       Шляхи і засоби розвитку логічного мислення………………….9
4.       Вимоги до системи навчальних завдань, які направлені на розвиток логічного мислення............................................................12

Розділ 2. Застосування розвиваючих завдань на уроках математики 5- 6 класів для розвитку логічного мислення.  ......................................................16

1.       Побудова  системи розвиваючих завдань, які направлені на розвиток логічного мислення учнів 5-6 класів................................16
2.       Методичні рекомендації щодо використання складеної системи задач….................................................................................................24

Висновки ............................................................................................................34

Список використаної літератури .....................................................................35

Додатки................................................................................................................37

 

 

 

 

 

 

 

 

Вступ

 

                                                                      “ Не думкам потрібно навчати,

                                                                       а навчати мислити.”

                                                                                                           Е. Кант                        

                                                   “Розумова праця на уроках

                                                   математики – пробний камінь мислення. ”

                                                                                                  І.Д. Новиков

          Необхідною умовою якісного оновлення суспільства є збільшення його інтелектуального потенціалу. Рішення цієї задачі багато в чому залежить від побудови освітнього процесу. Найважливіше завдання школи з питань навчання математики – це вміння давати глибокі та міцні знання, прищеплювати навички й уміння застосовувати їх на практиці. Школа повинна навчити учнів знаходити шляхи до розв’язання проблем, формувати здатність до самостійного, творчого мислення. Потреба в цілеспрямованому формуванні логічного мислення в процесі вивчення конкретних освітніх дисциплін вже усвідомлюється психологами і педагогами. Робота над розвитком логічного мислення йде без усвідомлення значущості психологічних прийомів і засобів в цьому процесі. Це приводить до того, що більшість учнів не опановують прийоми систематизації знань на основі логічного мислення навіть в старших класах школи.

          У зв’язку із збільшенням розумового навантаження на уроках математики вчитель має замислитися над тим, як підтримати інтерес учня до матеріалу упродовж усього уроку, щоб на уроках не було байдужих спостерігачів, а лише активні учасники навчального процесу, оскільки з цього виникає й розвивається допитливість і глибокий пізнавальний інтерес. При цьому інструментом для розвитку мислення, є нестандартні завдання (завдання на «міркування», логічні завдання, головоломки). Їх можна успішно використовувати на уроках як додаткові, допоміжні шляхи для тренінгу мислення і формування елементів творчої діяльності. Учні повинні уміти розв’язувати  не лише стандартні завдання, але і ті що вимагають незалежного мислення, оригінальності, винахідливості.

          На Заході ще в середні віки педагоги прагнули оживити і зробити більш цікавим викладання “ сухої “ математики.

Розділ І. Теоретичні аспекти проблеми розвитку логічного мислення учнів на уроках математики

1.1. Проблема розвитку мислення в процесі навчання.

Проблема розвитку мислення в різні часи розглядалася різними психологами. Сучасна психологічна наука розуміє мислення як вищий пізнавальний процес. Проблемою розвитку мислення учнів займалися багато зарубіжних і вітчизняних учених: П. Я. Гальперін, В. В. Давидов, Д. Дьюі, А. Н. Леонтьєв, В. К.Ягодовська, А. С.Пчелко Н. С., Л. Микольська, Ж. Піаже, С. А. Рубінштейн, А. А. Столяр, Д. Б. Ельконін, Ю. И. Шрайнер, Т. З Верінг., Л. С.Виготський, И. Я. Лернер, Н. А. Менчинска, Д. Н. Середа, М. Н. Скаткін та ін.. Вони теоретично і експериментально довели, що і сьогодні школа ще не досить забезпечує випускникам необхідний рівень розвитку розумової діяльності. Логічне мислення дає відповідь на такі питання, які не можна дозволити  розв'язати  шляхом безпосереднього, чуттєвого відображення. Завдяки розвитку індивідуальних якостей мислення, людина правильно орієнтується у навколишньому світі, використовуючи раніше отримані узагальнення в новій, конкретній обстановці. Кожне покоління людей пред'являє свої вимоги до школи. Раніше первинним завданням вважалося озброєння учнів глибокими знаннями, уміннями і навичками. Сьогодні завдання загальноосвітньої школи інші. На перший план виходить формування універсальних учбових дій, що забезпечують школярам уміння вчитися, здатність в масі інформації відібрати потрібне, саморозвиватися і самоудосконалюватися. З'явилися нові Державні освітні стандарти загальної освіти другого покоління, в яких прописано, що головною метою освітнього процесу є формування універсальних учбових дій, таких як: особистісні, регулятивні, пізнавальні, комунікативні. У відповідності стандартам другого покоління пізнавальні універсальні дії включають: загальнонавчальні, логічні, а також постановку і вирішення проблеми.[16, стр.28].

До логічних універсальних дій відносяться:

- аналіз об'єктів з метою виділення ознак (суттєвих, несуттєвих);

 - синтез - складання цілого з частин, у тому числі самостійне добудовування із заповненням бракуючих компонентів;

- вибір підстав і критеріїв для порівняння,  класифікації об'єктів;

 - підведення під поняття, виведення наслідків;

- встановлення причинно-наслідкових зв'язків;

 - побудова логічного ланцюга міркувань;

 - доказ;

- висунення гіпотез і їх обґрунтування.

Ніхто не сперечатиметься з тим, що кожен вчитель повинен розвивати логічне мислення учнів. Про це говориться в методичній літературі, в пояснювальних записках до навчальних програм. Практика навчання показує, що розвиток мислення учнів ставиться метою уроку практично по кожному предмету. Вважалося, що на уроках математики логічне мислення розвивається автоматично, без цілеспрямованої роботи.

Як показує аналіз літератури, існують різні види мислення

 

 

 

 

 

 

 

 

 

 

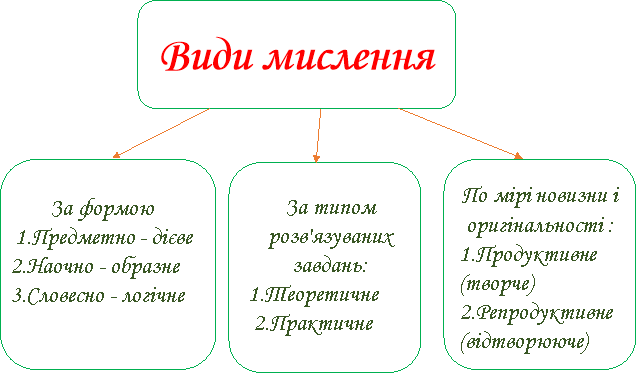
Слід зазначити, що усі види мислення тісно взаємозв'язані між собою. Тому, намагаючись визначити вид мислення, слід пам'ятати, що цей процес завжди відносний і умовний. Про людину, у якої добре розвинене логічне мислення, говорять, що він ґрунтовно мислить, дисципліновано міркує. Така людина, як правило, не допускає помилок у своїх міркуваннях і висновках. Добре розвинене логічне мислення застерігає людину від промахів і помилок в практичній діяльності. І ця якість розвивається головним чином в процесі вивчення математики, бо математика - це практична логіка, в ній кожне нове положення отримане за допомогою строго обґрунтованих міркувань на основі раніше відомих положень, тобто строго доводиться. Математика привчає до логічного мислення. У математиці учень з найбільшою повнотою, найбільш опукло і зримо може побачити демонстрацію майже усіх основних законів елементарної логіки.

1.2 Суть розвитку логічного мислення дітей середнього шкільного віку

      Мислення - це опосередковане і узагальнене відображення дійсності, вид розумової діяльності, що полягає в пізнанні суті речей і явищ, закономірних зв'язків і стосунків між ними [15, с.9]. Дослідження дитячого мислення і його розвитку, зокрема переходу від практичного до логічного, були розпочаті Л. С. Виготським. Їм же були намічені основні шляхи і умови цього переходу. На розумінні ролі практичної дії як початковому рівню процесу розвитку всіх вищих форм мислення людини побудована концепція “поетапного формування розумової дії”, розроблена П. Я. Гальперіним. [5, с.53] На першому етапі дитина використовує для вирішення завдання зовнішні матеріальні дії. На другому ці дії лише представляються і промовляються дитиною (спочатку голосно, потім про себе). Лише на останньому, третьому етапі зовнішня наочна дія “згортається” і вирушає у внутрішній план.

          Логічне мислення, на думку А. А. Люблінською, виявляється, перш за все, в протіканні самого розумового процесу. На відміну від практичного, логічне мислення здійснюється лише словесним шляхом. Людина повинна міркувати, аналізувати і встановлювати потрібні зв'язки в думках, відбирати і застосовувати до даного йому конкретного завдання відомі йому відповідні правила, прийоми, дії.

Він повинен порівнювати і встановлювати шукані зв'язки, групувати різне і розрізняти схоже, і все це виконується лише за допомогою розумових дій. Величезне значення в учбовій діяльності  школяра має операція порівняння. Адже велика частина матеріалу, який засвоює учень,  побудована на порівнянні. Ця операція лежить в основі класифікації явищ і їх систематизації. Для оволодіння операцій порівняння людина повинна навчитися бачити схоже в різному і різне схожому. Вдосконалення логічних висновків зберігається і в інших розумових процесах: у встановленні причинно-наслідкових зв'язків, в класифікації і відповідях на поставленні дорослими питання, що вимагають планування, здогадки, пошуку рішення. Розвитку мислення в середньому шкільному віці належить особлива роль. З початком навчання, мислення висувається в центр психічного розвитку дитини і стає  визначним в системі інших психічних функцій, які під його впливом інтелектуалізуються і набувають довільного характеру [15, с.12].

     У. У. Сойєр в книзі «Прелюдія до математики» [23,с.167] відзначає: «Можна навчити учнів вирішувати достатньо багато типів завдань, але справжнє задоволення прийде лише тоді, коли ми зуміємо передати нашим вихованцям не просто знання, а гнучкість розуму, яка дала б їм можливість надалі не лише самостійно вирішувати, але і ставити перед собою нові завдання». У нових освітніх стандартах сказано: «При навчанні різним предметам використовуються завдання, які прийнято називати учбовими. З їх допомогою формуються наочні знання, уміння, навички. Особливо широко застосовуються завдання в математиці, фізиці, хімії, географії. Як правило, в них використовуються математичні способи рішення. » [16, с.91].

     Найважливішим завданням математичної освіти є озброєння учнів загальними прийомами мислення, просторової уяви, розвиток здатності розуміти сенс поставленого завдання, уміння логічно міркувати, засвоїти навички алгоритмічного мислення.

1.3. Шляхи і засоби розвитку логічного мислення   

    На відміну від багатьох навчальних дисциплін математика оперує абстрактними поняттями. Продемонструвати всі предмети вивчення або процеси не є можливим. Це і викликає складність у дітей в її освоєнні. Для вчителя важливо не навчати дітей вирішувати задачі за зразком, а сприяти розвитку розумової діяльності. Основними результатами такого підходу є: розвиток самостійності, що важливе для навчання в старших класах; розуміння помилок і причин їх виникнення в процесі розв'язання прикладів і завдань; усвідомлення джерел, які потрібні для виконання завдань; вдосконалення творчих і логічних операцій; підвищення швидкості виконання завдань. Залежно від віку учнів педагог підбирає відповідні інструменти. Вони можуть бути направлені на порівняння, аналіз або синтез, абстракцію, класифікацію або будову висновків.  Сприймати одночасні декілька об'єктів здатний кожен. Але чим старше учень, тим більше він може утримувати предметів в пам'яті. Це також слід враховувати в ході вчення.

    Можна виділити два підходи до формування і становлення логіко-математичного мислення:

• традиційне навчання, що приводить залежно від дії і інших об'єктивних причин до формування або емпіричного, або теоретичного мислення;
• спеціально організоване навчання, орієнтоване на формування учбової діяльності, що приводить до становлення теоретичного мислення. Для формування логічного мислення пріоритетним є другий підхід.

Основним засобом розвитку математичних здібностей учнів є нестандартні задачі. Не випадково відомий сучасний математик Д. Пойа пише: «Що означає володіння математикою? Це є уміння розв'язувати  задачі, причому не лише стандартні, але і ті, які вимагають відомої незалежності мислення, здорового глузду, оригінальності, винахідливості».

    У системі завдань шкільного курсу математики, безумовно, необхідні завдання, направлені на відпрацювання того або іншого математичного навику, завдання ілюстративного характеру, тренувальні вправи, що виконуються за зразком. Але не менш необхідні завдання, направлені на виховання в учнів стійкого інтересу до вивчення математики, творчого відношення до навчальної діяльності математичного характеру. Необхідні спеціальні вправи для навчання школярів способам самостійної діяльності, загальним прийомам вирішення завдань, для оволодіння ними методами наукового пізнання реальної дійсності і прийомам продуктивної розумової діяльності, якими користуються учені-математики, вирішуючи ту або іншу задачу. Здійснюючи цілеспрямоване навчання школярів вирішенню завдань, за допомогою спеціальний підібраних вправ, можна учити їх спостерігати, користуватися аналогією, індукцією, порівняннями, і робити відповідні висновки.

     При вирішенні нестандартних завдань розвиваються уява і фантазія, пам'ять і увага, гнучкість мислення, розум дитини стає гострішим, формуються уміння спостерігати, аналізувати явища, проводити порівняння, узагальнювати факти, робити виводи. Міркування учнів стають – послідовними, доказовими, логічними, а мова - чіткою, переконливою і аргументованою. Вирішення нестандартних завдань – зовсім не привілей математики. Саме в ході вирішення таких завдань найприроднішим способом можна формувати у школярів елементи творчого математичного мислення поряд з реалізацією безпосередніх цілей вчення математики.

     Нестандартні завдання діляться на 2 категорії:

1 категорія. Завдання, що примикають до шкільного курсу математики, але підвищеної складності – по типу завдань математичних олімпіад.

2 категорія. Завдання по типу математичних розваг.

      Перша категорія нестандартних завдань призначається в основному для школярів з інтересом, що визначився, до математики; тематично ці завдання зазвичай пов'язані з тим або іншим певним розділом шкільної програми. Вправи, що відносяться сюди, поглиблюють навчальний матеріал, доповнюють і узагальнюють окремі положення шкільного курсу, розширюють математичний кругозір, розвивають навички у вирішенні важких завдань.

Друга категорія нестандартних завдань прямого відношення до шкільної програми не має і, як правило, не передбачає великої математичної підготовки. Це не означає, проте, що в другу категорію завдань входять лише легкі вправи. Тут є завдання з дуже важким розв’язками і такі завдання, розв'язування яких до цих пір не отримане.

      Ефективність формування логічних знань і вмінь учнів забезпечується застосуванням різних методів навчання, використанням різноманітних форм організації знань, раціональним співвідношенням фронтальної, індивідуальної й групової форм роботи. Одним із найбільш впливових засобів формування логічного мислення учнів є система вправ із логічним навантаженням .

 Основні теоретичні позиції у формуванні логічних знань і вмінь учнів :

- математичні вправи з логічним навантаженням повинні враховувати цілі навчання математики і створюватися на основі програмового матеріалу курсу

математики;

- структуру системи вправ потрібно визначити, спираючись на загальні психологічні закономірності сприйняття, мислення, уваги, пам’яті та особливості логічного мислення школярів;

- у системі повинні реалізовуватися принципи розвивального навчання і загально дидактичні принципи;
- виконання системи вправ з логічним навантаженням повинно забезпечувати засвоєння учнями математичних знань на основному, підвищеному і поглибленому рівнях, а логічних знань – на репродуктивному, продуктивному і творчому рівнях.

Поняття « система вправ з логічним навантаженням» не повинна розумітися як тільки розв’язування задач або вправ з логічним навантаженням. Це цілеспрямована система роботи вчителя над розвитком логічного мислення учнів на кожному етапі уроку . Досвід роботи вчителя показує, як через систему вправ з логічним навантаження можливо розвивати логічне мислення школярів на етапі мотивації, при перевірці домашнього завдання, при вивченні нової теми, при узагальненні та систематизації знань, умінь та навичок, як наприкінці уроку, так і при закінчення вивчення розділу.

Формування мотиваційного компонента здійснюється через забезпечення позитивного ставлення учнів до математичної діяльності; виховуючи пізнавальний інтерес. На уроках використовуються вислови відомих особистостей. Зародження процесу логічного мислення вимагає наявності проблемної ситуації.

Учень лише тоді буде працювати активно і плодотворно, коли ситуація, що виникла, буде для нього особистісно близькою. Необхідними на цьому етапі є

особистісна активність стосовно проблеми, чітке розуміння питання, усвідомлення суб'єктом протиріччя між особистим досвідом і необхідним обсягом знань, прагнення розв'язати проблему, бажання саморозвитку.

Внутрішня мотивація у багатьох учнів ще нестійка і залежить від ситуації. Тому

вчитель пропонує логіко розвивальні завдання, цікаві факти з життя знаменитих людей, різноманітні історичні матеріали, ігрові ситуації, розв’язання ситуативних задач .

1.4 Вимоги до системи навчальних завдань, які направлені на розвиток логічного мислення

   Для формування логічного мислення пріоритетним є навчання орієнтоване на формування учбової діяльності, що приводить до становлення теоретичного мислення. Основним засобом розвитку математичних здібностей учнів є задачі. Не випадково відомий сучасний математик Д. Пойа пише: «Що означає володіння математикою? Це є уміння вирішувати завдання, причому не лише стандартні, але і ті які вимагають відомої незалежності мислення, здорового глузду, оригінальності, винахідливості».

     Одна з головних причин труднощів учнів, які вони мають при розв'язанні задач, полягає в тому, що математичні завдання, що містяться в основних розділах шкільних підручників, як правило, обмежені однією темою. Їх розв'язання  вимагає від учнів знань,  умінь і навиків по якому-небудь одному питанню програмного матеріалу і не передбачає широких зв'язків між різними розділами шкільного курсу математики.

       Роль і значення таких завдань вичерпуються на протязі того нетривалого періоду, який відводитися на вивчення (повторення) того або іншого питання програми. Функція таких завдань найчастіше зводитися до ілюстрації теоретичного матеріалу, що вивчається, до роз'яснення його сенсу. Тому учням неважко знайти метод розв'язання даної задачі. Цей метод інколи підказується назвою розділу підручника або задачника, темою, що вивчається на уроці, вказівками вчителя і так далі. Самостійний пошук методу розв'язання учнем тут мінімальний. Під час розв'язання  завдань на повторення, що вимагають знання декілька тем, в учнів, як правило, виникають певні труднощі.

      На жаль, в практиці навчання математиці вирішення завдань найчастіше розглядається лише як засіб свідомого засвоєння школярами програмного матеріалу. І навіть завдання підвищеної складності спеціальних збірок, призначених для позакласної роботи, в основному мають на меті закріплення умінь і навиків учнів в розв'язанні стандартних завдань, завдань певного типу. А тим часом функції завдань дуже всілякі: навчальні, розвиваючі, виховні, контролюючі.

      Кожна запропонована для розв'язання учням нестандартна задача може слугувати багатьом конкретним цілям навчання. Та все ж головна мета нестандартних завдань — розвинути творче мислення учнів, зацікавити їх математикою, привести до «відкриття» математичних фактів. Досягти цієї мети за допомогою одних стандартних завдань неможливо, хоча стандартні завдання, безумовно, корисні і необхідні, якщо вони дані вчасно і в потрібній кількості. Слід уникати великого числа стандартних завдань як на уроці, так і в позакласній роботі, оскільки в цьому випадку сильні учні можуть втратити інтерес до математики. Ознайомлення учнів лише із спеціальними способами розв'язання окремих типів завдань створюють, на мій погляд, реальну небезпеку того, що учні обмежаться засвоєнням одних шаблонних прийомів і не придбають уміння самостійно вирішувати незнайомі завдання.

    Необхідні спеціальні вправи для навчання школярів способам самостійної діяльності, загальним прийомам розв'язання задач, для оволодіння ними методами наукового пізнання реальної дійсності і прийомам продуктивної розумової діяльності, якими користуються учені-математики, вирішуючи ту або іншу задачу. Здійснюючи цілеспрямоване навчання школярів розв'язанню задач, за допомогою спеціальний підібраних нестандартних завдань, можна навчати їх спостерігати, користуватися аналогією, індукцією, порівняннями, і робити відповідні висновки.

    Необхідно на уроках систематично використовувати нестандартні завдання, сприяючі цілеспрямованому розвитку логічного мислення учнів, їх математичному розвитку, формуванню у них пізнавального інтересу і самостійності. Такі завдання вимагають від школярів кмітливості, спостережливості, творчості і оригінальності. Нестандартні завдання багатогранні, але їх об'єднує наступне:

• спосіб розв'язання  нестандартних задач не відомий. Для їх розв'язання характерний, броунівський рух думки, тобто до розв'язання призводить метод проб і помилок. Пошукові спроби розв'язання можуть в окремих випадках закінчитися здогадкою, яка є знаходженням шляхів шуканого розв'язку;
• нестандартні завдання сприяють підтримці інтересу до предмету і грають роль мотивації до діяльності учнів. Незвичність сюжету, способу презентації завдання знаходять емоційний відгук у дітей і ставлять їх в умови необхідності її розв'язання;
• нестандартні завдання складені на основі знань законів мислення.

    Систематичне використання нестандартних завдань сприяє розвитку вказаних розумових операцій і формуванню математичних уявлень дітей. Для вирішення таких завдань характерний процес шуканих проб. Поява здогадки свідчить про розвиток у дітей таких якостей розумової діяльності, як кмітливість. Ці якості розумової діяльності можна і потрібно розвивати в процесі навчання.

    У будь-якому випадку здогадці як способу розв'язання задачі передує ретельний аналіз: виділення в завданні істотних ознак, просторового розташування і узагальнення ряду фігур, їх властивостей, схожих ознак і тому подібне Проте для розв'язання нестандартних завдань метод проб і помилок ненадійний і нераціональний. Набагато ефективніший спосіб – озброїти дітей тими прийомами розумової діяльності, які необхідні при цьому: аналіз і синтез, порівняння, аналогія, класифікація. Пропонуючи учням нестандартні завдання, ми формуємо у них здатність виконувати ці операції і одночасно розвиваємо їх. Звичайно, не можна привчати учнів розв'язувати лише ті завдання, які викликають у них інтерес. Але не можна і забувати, що такі завдання учень вирішує легше і свій інтерес до розв'язання однієї або декількох завдань він може надалі перенести і на «нудні» розділи, неминучі при вивченні будь-якого предмету, у тому числі і математики. Таким чином, вчитель, що бажає навчити школярів розв'язувати завдання, повинен викликати у них інтерес до нестандартного завдання, переконати, що від розв'язання математичної задачі можна отримати таке ж задоволення, як від розв'язання нестандартних завдань. Вчитель, що викладає в 5-6 класах, може розвивати логічне мислення учнів за допомогою створеної системи нестандартних завдань. Для цього необхідно враховувати наступне:

   1. Нестандартні завдання мають бути посильними для дітей.

   2. Нестандартні завдання, відібрані для одного уроку, мають бути всілякими для взаємодії на різні компоненти мислення.

   3. Якщо учні не справляються з розв'язанням нестандартних завдань, то доцільно залишити його на обдумування до наступного уроку.

   4. Учням можна дати необов'язкове домашнє завдання по складанню аналогічних нестандартних завдань.

   5. Якщо на уроці час обмежений, то нестандартні завдання можна застосовувати на заняттях математичного кружка.

   Таким чином, хорошим засобом навчання розв'язуванню завдань, засобом для знаходження плану розв'язання є нестандартні завдання.

Розділ 2. Застосування розвиваючих завдань на уроках математики 5- 6 класів для розвитку логічного мислення. 

   2.1 Побудова  системи розвиваючих завдань, які направлені на розвиток логічного мислення учнів 5-6 класів

     Математику люблять в основному ті учні, які уміють розв'язувати задачі. Отже, навчивши дітей володіти умінням розв'язувати нестандартні завдання, ми зробимо істотний вплив на їх інтерес до предмету, на розвиток логічного мислення і мови. Крім того, вони є потужним засобом активізації пізнавальної діяльності, тобто викликають у дітей величезний інтерес і бажання працювати. Узявши учнів 5-Б класу у вересні 2017 році  я провела методики «Четвертий зайвий» і «Числові ряди» з використанням картинок і серії завдань на визначення рівня сформованості логічного мислення. Результати досліджень: всього в класі – 20 учнів, з них :

високий рівень- 2 учня ( 10 %) ;

середній рівень – 7 учнів ( 35 %);

низький рівень- 11 учнів ( 55 %)

        Висновок: рівень сформованості логічного мислення розвинений слабо, клас має низьку мотивацію до навчання. Тому я поставила перед собою мету викликати зацікавленість до математики за допомогою нестандартних розвиваючих завдань, привернути їх увагу. Для здійснення поставленого завдання необхідно скласти систему нестандартних завдань по темах.

      Підручник математики для учнів 5 класу повинні містити велику кількість не лише нестандартних завдань, але і завдань цікавого характеру:

 • Завдання на розрізання і складання фігур;

 • Завдання з сірниками;

 •  Математичні ребуси;

 • Математичні ігри;

 • Комбінаторні завдання;

 • Логічні завдання і ін.

      Але окрім цікавих завдань можна запропонувати цикл завдань, які розв'язуються нетрадиційно. Це завдання виду:

Завдання на припущення.

 Аналіз умови завдань даного виду приводить до необхідності зіставлення двох  груп об'єктів, схожих по суті, але таких,  що мають відмінні ознаки (наприклад, різна кількість ніг, коліс, сторінок і т. п.).

Підготовча робота.

Мета підготовчої роботи:

 —уточнення представлень учнів про окремі об'єкти дійсності;

—усвідомлення характеру залежності однієї величини від іншої, оскільки від кількості об'єктів кожного виду залежить сумарне значення їх відмітних характеристик. 

  Приклади підготовчих вправ

1. Дай відповідь на запитання: «Скільки лап у чотирьох собак? Скільки ніжок у двох стоног? На скільки лап у п'яти собак більше, ніж ніг в п'яти курей? Де більше пасажирів і на скільки: у трьох чотиримісних човнах або в п'яти двомісних?»

Методи розв'язання завдань на припущення.

 З а д а ч а. Потрібно розсадити 22 туриста в двомісні і чотиримісні човни. Скільки тих і інших човнів буде потрібно, якщо всього човнів 8?

 Практичний метод:

Розв'язання даної задачі може бути представлене послідовністю символічних малюнків. Ввівши відповідні позначення і виконавши практичні дії, перерахунком встановлюємо, що якщо в кожен човен посадити по 2 туристи, то в 8 човнах розмістяться лише 16 з 22 чоловік. Отже, 6 туристів розмістили по двоє (оскільки човни були і чотиримісні) в перші три човни.

   Таким чином знаходять відповідь на питання завдання. Підкреслимо, що практичне розв'язання задачі можна оформити за допомогою символічного малюнка, схеми, таблиці; завдання допускає розв'язання практичним методом за наявності невеликих числових даних в її умові; по ходу здійснення практичних дій доцільно фіксувати відповідні їм арифметичні операції.

     Арифметичний метод:

1) 2×8 = 16 (тур.) — розмістили по двоє в 8 човнах;

2) 22 – 16 = 6 (тур.) — залишилося розмістити;

3) 4 – 2 = 2 (місць) — більше в чотиримісному човні;

4) 6 : 2 = 3 (ч.) — чотиримісних;

5) 8 – 3 = 5 (ч.) — двомісних.

Перевірка: 2×5 + 4×3 = 22; 22 = 22.

     Алгебраїчний метод:

 Позначимо через x число двомісних човнів, тоді чотиримісних човнів 8 – x. Рівняння, складене за умовою завдання, матиме  вигляд: 2×х + 4×(8 – x)= 22. Розв'язання даного рівняння доступне лише учневі більш старшого шкільного віку.

      Метод перебору:

 Оформити послідовний перебір всіх варіантів в таблицю. Оскільки загальне число човнів дорівнює 8, то найбільш вдалим слід вважати підбір, починаючи з середнього варіанту — 4 чотиримісні човни і 4 двомісні човни. А потім, відштовхуючись від отриманого результату (22 туристи),вийти на розв'язання, зменшивши на 1 число чотиримісних човнів.

     Метод припущення відповіді:

 Передбачимо, що з 8 човнів лише 3 човни були двомісні, а останні 5 — чотиримісні. Взнаємо, скільки туристів можна розсадити в човни за цієї умови: 2×3 + 4×5 = 26 туристів. Отримали, що 26 > 22 (отримане число більше даної загальної кількості туристів). При прийнятій гіпотезі кількість туристів збільшилася б на 4, оскільки 26 – 22= 4. Приберемо з кожного чотиримісного човна по 2 туристи, оскільки в кожному чотиримісному човні на 2 місця більше, ніж в двомісній (4 – 2 = 2). Тепер взнаємо, на скільки прийнята гіпотеза більше дійсної відповіді: 4 : 2 = 2 човни, тому кількість чотиримісних човнів дорівнює 5 – 2 = 3, а двомісних 8 – 3 = 5 або 3 + 2 = 5 човнів. Способом встановлення відповідності між даними і шуканими легко визначається правильність розв'язання запропонованої задачі: 2×5 + 4×3 = 22, 22 = 22.

Задача на заміну даних.

    В умові цих задач є дані, зв'язані кратним або різницевим відношенням, що дозволяє при розв'язанні здійснити заміну одних даних на інших, не змінюючи загальної відомої величини (наприклад, вартості або маси покупки).

     Підготовча робота.

 Мета підготовчої роботи — усвідомлення учнями (у неявному вигляді, тобто без введення терміну) властивостей прямої і зворотної пропорційної залежності: із збільшенням (або зменшенням) однієї величини збільшується (або зменшується) інша (при постійній третій). Наприклад, чим дорожче ціна, тим менше предметів можна купити на наявні гроші. Важливо звернути увагу на збереження кратності відношень: у скільки разів більше ціна, в стільки разів менше кількість (при постійній вартості). Якщо величини зв'язані не кратним, а різницевим відношенням, то потрібне розуміння того, що заміна декількох великих величин такою ж кількістю менших веде за собою зменшення загальної кількості.

Приклади підготовчих вправ.

Розв'яжи задачу.

1. Для дитячого садка купили 4 м'ячі і 3 ляльки. Лялька в 2 рази дорожче за м'яч. Скільки ляльок можна було купити замість 4 м'ячів? Скільки всього ляльок можна було купити на всі гроші? Скільки м'ячів стоять стільки ж, скільки 3 ляльки?

    Методи розв'язування задач на заміну даних.

З а д а ч а 1. Мама купила 4 яблука і 3 груші, заплативши за всю покупку 50 р. Груша в 2 рази дорожче за яблуко. Скільки коштує яблуко? Скільки коштує груша?

       Алгебраїчний метод:

Алгебраїчний метод може використовуватися в неявному вигляді, тобто без введення терміну для назви способу рішення і латинських букв для позначення змінних. 4я + 3г = 50, але г = 2я ,

4я + 3•2я = 50,

4я + 6я = 50,

10я = 50 я = 5;

 г = 2•5 = 10

       Арифметичний метод:

 Спосіб 1

 1) 3×2 = 6 (яб.) — замість 3 груш;

2) 4 + 6 = 10 (яб.) — всього;

3) 50 : 10 = 5 (р.) — ціна яблука;

4) 5×2 = 10 (р.) — ціна груші.

Спосіб 2

 1) 4 : 2 = 2 (гр.) — замість 4 яблук;

2) 2 + 3 = 5 (гр.) — всього;

3) 50 : 5 = 10 (р.) — ціна груші;

 4) 10 : 2 = 5 (р.) — ціна яблука.

Перевірка: 5×4 + 10×3 = 50.

    Міркування таким методом можна поєднувати з практичними (схематичними) діями.

Завдання на відшукання чисел по їх сумі, різниці або кратному відншенню.

     Підготовча робота.

 Мета підготовчої роботи — формування умінь перекладати на математичну мову і схематично зображати різні твердження.

    Приклади підготовчих вправ.

1. Знайди 2 числа, якщо їх:

а) сума дорівнює 20, а різниця 10;

 б) сума дорівнює 100, а частка 9;

в) різниця дорівнює 20, а сума 100;

г) різниця дорівнює 30, а частка 2.

2. Одне число більше за інше в 3 рази, а їх сума дорівнює 60. Знайди ці числа.

Методи вирішення завдань на відшукання чисел по їх сумі, різниці або кратному відношенню.

З а д а ч а 1. На шкільній ділянці посадили 20 лип і кленів, причому на кожну липу приходиться 4 клена. Скільки лип посадили?

      Практичний метод:

Змалюємо кожне дерево символом. Відомо, що на кожну липу доводяться 4 клени. Тому кожному символу, що позначає липу, поставимо у відповідність чотири символи клена.

       Арифметичний метод:

1) 1 + 4 = 5 (частин) — в загальній кількості;

2) 20 : 5 = 4 (дер.) — в одній частині;

3) 1×4 = 4 (липи);

4) 20 – 4 = 16 або 4×4 = 16 (кленів)

 Л К 20 дерев 1 частина 4 частини

Завдання, що розв'язуються з «кінця».

       Виділення даних завдань в окрему групу пов'язане із способом міркування при їх розв'язанні, яке виконується до  «кінця» задачі. У методичній літературі він названий методом інверсії або звернення. Суть його полягає в наступному: якщо треба знайти число, яке після ряду операцій приводить до відомого числа, то для цього необхідно з даним числом виробити в зворотному порядку всі зворотні операції. Цим правилом часто користувалися при розв'язуванні задач індійські, потім арабські і західноєвропейські математики. Вони формулювали його так: «Множення стає діленням, ділення множенням, то що було виграшом (складання), стає втратою (віднімання) і навпаки».

     Підготовча робота.

Мета підготовчої роботи: —уточніть сенс слів половина, чверть, третя частина і т. п.;

 —усвідомити суть поняття зворотна операція;

 —актуалізувати спосіб знаходження числа по відомій частині.

     Приклади підготовчих вправ.

1. Задумано число, якого рівні 8. Яке число задумане?

2. Петя прочитав 20 сторінок, що складає загального числа сторінок в книзі. Скільки всього сторінок в книзі?

      Методи вирішення завдань, що вирішуються з «кінця».

З а д а ч а. Жінка продавала яблука. Перша покупниця  купила у неї половину всіх яблук і ще пів яблука, друга — половину тих, що залишилися і ще пів яблука, а третя купила останні 5 яблук. Скільки яблук принесла жінка на продаж?

       Арифметичний метод:

По ходу засвоєння змісту задачі необхідно скласти схему у відрізках, яка надасть істотну допомогу в її розв'язанні. На початковому етапі навчання розв'язуванню задач такого вигляду доцільно пропонувати учням схему в готовому вигляді.

      Розв'язання (міркування з кінця» задачі):

 1) 5 + 1/2 = 5 1/2— яблук в половині залишку;

2) 5 1/2+ 5 1/2 = 11 — яблук в залишку;

 3) 11 + 1/2= 11 1/2— яблук в половині всієї кількості;

4) 11 1/2+ 11 1/2= 23 — всього яблук.

      Метод підбору.

 Якщо в завданні невеликі числові дані, то при її розв'язанні можна скористатися методом підбору. Раціональний підбір передбачає перш за все попередню прикидку можливої кількості яблук. З умови завдання виходить, що їх чисельне значення дещо більше 20, оскільки 5 яблук менше, ніж чверть їх загальної кількості. Припустимо, що яблук могло бути 21, 22, 23,24 або 25. Проте усвідомлення умови «половина і ще пів-яблука» приводить до виводу, що кількість яблук — непарне число. Залишаються числа 21, 23 і 25. З виділених чисел краще всього перевірити першим середнє по величині —23. Якщо всі умови виконуються, то розв'язок знайдений, інакше, залежно від отриманого в ході перевірки результату, слід зробити ще одну спробу.

Завдання на спільну роботу.

Ці завдання відносяться до завдань на процеси. Їх відмінною особливістю є наявність в умові лише одній величини, що характеризує процес роботи (часу), тоді як для визначення невідомої величини необхідно, щоб було відомо дві величини. Розв'язання задач даного вигляду ґрунтується на умовному прийнятті невідомої величини (роботи) за одиницю.

      Підготовча робота.

Цілі підготовчої роботи: —актуалізувати знання учнів про величини об'єм, робота, продуктивність, час і взаємозв'язки між ними, вираженої у формулі роботи;

—уточнити неявні (без введення терміну) уявлення учнів про загальний кратний декількох чисел;

—потренувати в розташуванні дробових чисел з різними знаменниками на числовому промені;

 —сформувати уміння ділити відрізок на рівні частини.

      Приклади підготовчих вправ.

 1. Познач на числовому промені числа, 1/3, 3/4, і тому подібне (Довжина одиничного відрізання має бути кратна 12.)

 2. Одиничний відрізок якої довжини потрібно змалювати, щоб розмістити на нім числа,4/9, 7/18, 5/6, і т. п.?

      Методи розв'язування задач на спільну роботу.

 - Графічний метод;

 -Арифметичний метод.

Завдання на рух.

 В основі виділення цього вигляду завдань в окрему групу лежить їх зміст: традиційно до них відносяться задачі, пов'язані з величинами швидкість, час, відстань, — на рух одного або двох об'єктів, що переміщуються з різною або однаковою швидкістю, по прямих або кривих траєкторіях, із зупинками або без них, що зближуються, віддаляються, рухаються за течією річки або проти течії.

    Їх можна розподілити на чотири групи.

1. Завдання на вертикальний рух із спуском.

2. Завдання на рух одного об'єкту між двома об'єктами, що зближуються.

3. Завдання на рух мимо об'єктів з врахуванням їх протяжності.

4. Завдання на рух об'єктів, що переміщаються в одному напрямі (навздогін, з відставанням).

      Підготовча робота

  Мети підготовчої роботи:

 —актуалізувати знання  учнів про залежність між величинами, що характеризують процес руху (швидкість руху, час, відстань), і здібність до її використання при вирішенні завдань на рух одного об'єкту;

—актуалізувати уявлення про швидкість як величину, яка характеризує прудкість руху; —систематизувати знання про одиниці часу, довжини, швидкості і співвідношеннях між ними (оскільки при вирішенні завдань на рух від учнів буде потрібно уміння працювати з іменованими числами, вираженими в одиницях різних найменувань, тобто здійснювати переведення одних одиниць виміру довжини, часу, швидкості в інші).

            Методи розв'язування задач на рух.

 - Графічний метод;

 -Арифметичний метод.

    Проте остаточна думка про користь, місце і час вживання кожної із запропонованих задач у навчанні школярів математиці може зробити лише вчитель.

 2.2 Методичні рекомендації щодо використання складеної системи задач

    Власне, одне з основних призначень системи нестандартних завдань і полягає в тому, щоб активізувати розумову діяльність учнів на уроці [24, з 12-15].

     Ефективність навчальної діяльності по розвитку логічного мислення багато в чому залежить від міри творчої активності учнів під час розв'язування системи нестандартних завдань. Система нестандартних завдань, повинна активізувати розумову діяльність школярів. навчання на даних уроках орієнтоване на розвиток логічного мислення учня – він виступає в ролі дослідника, творця, вчитель – в ролі невидимого керівника.

      Навчаючи дітей по даному методу, можна виявити наступні зміни в особистості школяра, а саме:

 – в учнів (відповідно до можливостей кожного) розвивається логічне мислення, уява, усна мова;

 – діти навчаються творчо виконувати будь-яке поставлену навчальну задачу;

– з'являється інтерес до математики.

        Отже, завдання вчителя під час будь-якого етапу уроку зацікавити дітей до розв'язування нестандартних завдань. Розвинути логічне мислення, спонукати їх творчо мислити, викликати азарт розв'язку нестандартної задачі; показати красу саме складного завдання і, звичайно ж, забезпечити ситуацію успіху. З метою його реалізації можна запропонувати в структуру уроку по математиці включити наступні етапи:

1. активізацію процесів уваги і сприйняття;

2. актуалізацію логічної операції за допомогою пам'яті, сприйняття, уяви;

3. здобуття цілісного уявлення про досліджуваний математичний об'єкт;

4. виявлення алгоритму розв'язування нестандартної задачі;

5. закріплення матеріалу;

6. контроль отриманих знань.

     На кожному уроці використовувати завдання, направлені на розвиток розумової операції. Протягом 5–8 хвилин проводити усний рахунок, в який включати розвиваючі нестандартні завдання на розвиток логічного мислення. Також учням пропонується конкретне нестандартне завдання, розв'язання якого має бути виконане на уроці. Провідна роль під час актуалізації логічної розумової діяльності тут належить вчителеві. Залежно від поставленої мети, він формулює і ставить питання по умові завдання. Причому питання складаються так, щоб направити мислення дитини на вірний хід  розв'язання нестандартної задачі. Розв'язання поставленої задачі потрібно запропонувати учням. Вчитель лише певним чином координує їх діяльність, направляючи міркування дітей за допомогою навідних питань. На цьому етапі використовувалися переважно групові форми роботи і робота у дошки. Складання алгоритму розв'язання математичної задачі здійснюється шляхом «програвання» в думці конкретних дій і маніпуляції з об'єктами. Обов'язково проводити закріплення матеріалу. Клас можна розбити на декілька груп, кожна окремо розв’язувала нестандартну задачу, а потім розв'язки порівнювалися; розбір розв'язку нестандартної задачі у дошки з коментуванням і тому подібне. І звичайно, поточний контроль засвоєння знань здійснюється на всіх уроках за допомогою індивідуального контролю, взаємоперевірки учнів, проведення змагань між групами за розв'язанню задач. На деяких уроках проводилися самостійні роботи.

      Для формування мотивації доцільно використовувати такі прийоми:

1. Дивуй.

Найбуденніші й повсюдні явища, події, предмети можуть стати дивними , якщо на них подивитись з іншої точки зору. Здивування – початкова фаза розвитку пізнавального інтересу. Такі вправи не тільки породжують пізнавальний інтерес, а розвивають логічне мислення учнів.
2) Відстрочена загадка.

На початку уроку вчитель дає загадку, відгадку на яку можна дізнатись на уроці під час роботи над новим матеріалом.

Наприклад при вивченні властивостей множення дітям пропонується на початку уроку підрахувати значення виразу 25* 4568*4 і підкреслюється, що вже сьогодні учні зможуть знайти відповідь на це питання усно, за лічені секунди.

2. Асоціації на дошці.

Цей метод якнайліпше розвиває у дитини логічне мислення, має високий рівень зацікавленості. Учитель записує на дошці основне поняття уроку, яке мають опрацювати учні. Далі він просить назвати асоціації, які воно у них викликає. Наприклад, при вивченні теми «Трикутник. Види трикутників. Периметр трикутника» вчитель записує на дошці слово «трикутник» , пропонує учням зібрати асоціації і записує їх поряд із словом «трикутник». Асоціації можуть бути різними ( три кути, три сторони, більярд, гострий, піраміда та ін.)

При перевірці домашнього завдання вчитель велику увагу приділяє перевірці теоретичних знань. Але, щоб вилучити момент заучування та заставити учнів міркувати питання ставляться таким чином, щоб діти розпочали міркувати. Наприклад пізнавальні завдання на протиставлення предметів:
1. Чим відрізняється об'єкт А від об'єкта В?

2. Яких властивостей немає в об'єкті А в порівнянні з об'єктом В?

3. Якими додатковими властивостями володіє об'єкт А в порівнянні з

об'єктом В?

4. Чим відрізняються формулювання...?

З метою розвитку логічного мислення вчитель застосовує такі прийоми:

- пропонуємо одне й те саме означення , якщо це можливо, визначити різними способами. Такі завдання розвивають мислення, надають розуміння певного об’єкта в повній мірі.

- встав пропущені слова або речення. Учням пропонується у означенні вставити пропущені слова, або речення.

- знайди помилку. Дітям дуже подобається шукати чужі помилки, особливо, коли її допустив вчитель. Тому можна запропонувати таке завдання: вчитель наголошує на тому , що він навмисно буде робити помилки у теоремі, означенні, формулі тощо, а учням потрібно її виправити.

     Роль простих задач у навчанні математики надзвичайно велика. Вони є основним засобом у формуванні поняття про арифметичні дії та величини. У процесі розв'язання простих задач учні опановують основні прийоми роботи над задачею. Високий рівень умінь розв'язувати прості задачі — необхідна умова успішного розвитку вмінь розв'язувати задачі складені. Навіть для найсильніших учнів усне розв'язання задач корисне: воно сприяє розвитку швидкості та гнучкості мислення, удосконалює вміння обчислювати та встановлювати функціональні залежності.

Вправи та задачі, що можна запропонувати учням для усного розв'язання перед вивченням складного матеріалу:

• Задача чи ні?

1. До Нового року діти робили з паперових квітів гірлянду. Їм потрібно було склеїти 56 квіток. Вони вже склеїли 35.
2. До годівниці насипали просо. Спочатку прилетіло 13 горобців, а потім — 9 синиць. Скільки проса вони з'їли?

• Задачі з недостатніми чи надлишковими даними

1. Бабуся пришила 6 ґудзиків, а потім — решту. Скільки всього ґудзиків пришила бабуся? Ваші пропозиції?
2. Біля годівниці сиділо 11 синиць. Прилетіло ще 9 синиць і 5 горобців. Скільки синиць біля годівниці?

• Задачі з непрямою залежністю величин 

У підручниках математики провідне місце посідають задачі з прямою залежністю величин. Розв'язуючи їх, учні звикають до прямого логічного зв'язку, зокрема, керуючись такими правилами: якщо «на стільки більше» — треба додати; якщо «на стільки менше» — відняти; якщо «у стільки разів більше» — помножити; «у стільки разів менше» — поділити.

Нерідко під час навчання дітей розв'язувати задачі з непрямою залежністю виникають труднощі, бо в них вже виробився певний стереотип.

Подолати його допомагає усне виконання поданих вправ і розв'язування нескладних задач на порівняння.

• Вправа «Логічні кінцівки». 

• Якщо стіл виший від стільця, то стілець... ( нижчий від стола).
• Якщо 10 більше ніж 9, то 9... (менше ніж 10).
• Якщо сестра старша за брата, то брат... (молодший від сестри).
• Якщо річка глибша від струмка, то струмок... (мілкіший за річку).
• Якщо Галинка із квартири вийшла раніше, ніж її братик, то братик вийшов... (пізніше).
• Якщо влітку день довший, то ніч... (коротша).
• Якщо права рука праворуч, то ліва... (ліворуч).

• Вправа «Доповни речення».

• Якщо одна величина більша від другої на кілька одиниць, то... (друга величина менша від першої на стільки ж одиниць).
• Якщо одна величина менша від другої на кілька одиниць, то... (друга величина більша від першої на стільки ж одиниць).
• Якщо одна величина більша від другої у кілька разів, то... (друга менша від першої у стільки ж разів).
• Якщо одна величина менша від другої у кілька разів, то... (друга більша у стільки ж разів).

У своїх рекомендаціях щодо навчання школярів К. Д. Ушинський писав: «...нехай вони вимірюють клас, двері, вікна, нехай перелічують сторінки своїх підручників і зошитів і про все це складають свої задачі, які поступово ускладнюватимуться, але ніколи не втрачатимуть свого практичного наочного характеру».

      Задача 1. У математичному турнірі беруть участь 7 учнів. Кожен учень знайомий принаймні з чотирма іншими. Доведіть, що серед учасників турніру є хоча б одна рійка учнів, знайомих між собою.

Розв’язування задачі починаємо з низки запитань, які допоможуть зрозуміти її умову.

• Давайте з’ясуємо, що означає: кожен учень знайомий принаймні з чотирма іншими? 
• Це означає, що він знайомий з 4, 5 чи 6 учнями. 
• Правильно, а чому не з 7 учнями? 
• Один з цих учнів – він сам, крім нього є ще 6 учнів. 
• А зі скількома учнями щонайбільше незнайомий будь-який учень? 
• З двома, оскільки 7 = 1 + 4 + 2, де 1 – це сам учень; 4 – знайомі йому учні; 2 – незнайомі. 
• Прочитайте уважно ще раз умову задачі. Що нам треба довести7 
• Треба довести, що серед учасників турніру є хоча б одна трійка учнів, знайомих між собою. 
• Поміркуйте, коли нашу задачу розв’язати найлегше: коли кожен учень знайомий з 4 учнями чи з 5, 6, і чому? 
• Якщо кожен учень знайомий з більшим числом учнів (5, 6), то серед усіх учнів легше вибрати трійку, що задовольняє умову задачі. Найскладніше у випадку, коли кожен знайомий тільки з 4 учнями. Тоді незнайомих між собою дітей буде найбільше. 
• Добре. Виберемо серед учнів двох, які між собою знайомі. Ми вже обґрунтували, що це можливо, назвемо їх умовно А (Андрій) і Б (Борис). Тоді скількох учнів вони вдвох щонайбільше не знатимуть? 
• Оскільки кожен з них не знає щонайбільше двох, то обидва не знатимуть щонайбільше чотирьох. 
• Оскільки 7 = 2 + 4 + 1, то двоє наших учнів обов’язково знатимуть одного учня. Назвемо цього учня умовно В (Василь). Що тоді можна сказати про трійку А, Б, В? 
• Усі вони знайомі між собою. 
• Отже, це і є та трійка, що задовольняє умову задачі. Підіб’ємо підсумок. Яке правило-орієнтир можна скласти для розв’язування цієї задачі? 

Правило-орієнтир 

1. З’ясуйте, зі скількома учнями може бути незнайомий кожен учень. 
2. Виберіть пару учнів, визначте кількість учнів, з якими вони можуть бути незнайомими. 
3. Серед тих учнів, що залишилися, виберіть одного, який з раніше обраною парою утворить трійку. Проаналізуйте, чи задовольняє умову задачі обрана трійка учнів.             
4. Завдання додому. Доведіть: якщо з 9 учнів кожен знайомий щонайменше з 5 учнями, то можна назвати трійку учнів, які були б знайомі між собою. 

1. Доведіть: якщо є 31 учень, з яких кожен знайомий щонайменше з 21 учнем, то можна назвати четвірку, які знали б один одного. 

Перш ніж розглянемо наступну задачу, давайте з’ясуємо: 

• Якщо є 6 чоловік, і вони потиснули руки один одному, то скільки всього було рукостискань? 

Відповідь: кожен учень потиснув руки п’яти іншим, разом рукостискань . Але кожне з них ураховано двічі, тому разом було  рукостискань.

Є 10 команд, які зіграли турнір в одне коло (без нічиїх, за перемогу дається 1 бал). Скільки всього балів отримано всіма командами?
Відповідь: оскільки кількість ігор , а за кожну гру отримано командою-переможцем 1 бал, то разом отримано 45 балів. 
Задача 2. Для відбору до команди знавців шість учнів провели турнір в одне коло, тобто кожен зіграв з будь-яким іншим учасником один раз. (Вважатиме­мо, що нічиїх немає. Гра продовжується до перемоги одного з учнів, за перемогу дається 1 бал). Доведіть, що можна назвати таких двох гравців, що кожен з решти учасників програв хоча б одному з цієї пари. 
Розв'язання. 

• Скільки ігор відбулося в турнірі? Скільки балів отримали всі учні разом? 
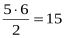•  ігор, стільки ж балів. 
• Скільки зустрічей було зіграно кожним учас­ником турніру? 
• Оскільки 6 = 1 + 5, то кожен гравець зіграв 5 ігор. 
• У результаті змагань гравці розташувалися в турнірній таблиці. Поміркуйте, скільки балів отри­мав учасник турніру, який зайняв І місце? Могло так статися, що він виграв усі 5 зустрічей і набрав 5 балів? 
• Так. 
• Чи міг якийсь інший гравець теж набрати 5 балів? 
• Ні, бо тоді він виграв би в усіх учнів, тобто й у першого, що є неможливим. 
• Добре, а чи могло так статися, що наш лідер, який зайняв перше місце, з п'яти ігор виграв менше половини, наприклад дві? Обґрунтуйте відповідь. 
• ?.. 
• Припустимо, що на першому місці учень (по­значимо його умовно А (Андрій)), який набрав 2 бали, що це означає? 
• Виграв дві зустрічі. 
• Так. Скільки тоді балів має учень, який зай­няв II місце? 
• Не більше 2 балів. 
• Якщо навіть кожен з учнів набере максималь­но можливі 2 бали, то яку найбільшу кількість балів наберуть усі учні? 
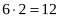• балів, але ж ми вже обчистили, що всі учні наберуть 15 балів за турнір, тому це неможливо. 
• Який висновок ми можемо зробити? 
• Наше припущення неправильне, отже, учень А виграв щонайменше 3 зустрічі, тобто 3, 4 або 5. 
• Скажіть, будь ласка, який випадок (3, 4 чи 5) — найскладніший? 
• Якщо учень А виграв усі 5 зустрічей, то пара учнів А та Б (будь-який учень) задовольняє умову задачі, оскільки кожен з решти гравців програв уч­неві А. Отже, найскладніший випадок, коли наш лідер (А) виграв 3 зустрічі. 
• Розглянемо цей випадок. Якщо учасник турні­ру виграв 3 зустрічі, то скільком учням він, можли­во, програв? 
• Оскільки 6 = 1 (А) + 3 (учні, у яких А виграв) + 2 (учні, про яких невідомо, чи виграв у них учень А, чи ні), то учень А, можливо, програв двом учням. 
• Давайте подивимося уважніше на цих двох учнів, що про них можна сказати, враховуючи умову задачі? 
• Вони обов'язково зіграти між собою, і хтось із них виграв у іншого. 
• Якщо ми переможця позначимо Б (Борис), що ми можемо сказати про пару А та Б? 
• Пара учнів А та Б задовольняє умову задачі, оскільки разом учнів 6, двоє з них — це А та Б, ще троє — ті, що програли А, один учень програв Б: 6 = 2 (А, Б) + 3 (програти А) + 1 (програв Б). 
• Підіб'ємо підсумок. Як ми з вами міркували? 

1. Разом учнів 6; кожен зіграв по 5 зустрічей; разом зустрічей 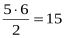; отже, всі учні разом на­брали 15 балів. 
2. Далі ми розташувати учасників у турнірній таблиці й припустили, що учень А, який зайняв пер­ше місце, виграв менше ніж половину своїх зустрі­чей. Виникла суперечність, і ми дійшли висновку, що А виграв принаймні 3 зустрічі, тобто виграв що­ найменше у трьох учнів. 
3. Учень А й ті 3 учасники турніру, в яких він виграв, не становлять усієї множини учнів, залиши­лося ще 2 учні (6 – 1 – 3 = 2). Серед цих двох учнів 
   ми вибрали переможця особистої зустрічі (Б). 
4. Пара учнів А, Б задовольняє умову задачі. 

Завдання додому. Є 14 команд, які провели між собою турнір в одне коло. (Вважається, що нічиїх немає. Гра продовжується до перемоги однієї з ко­манд). Доведіть, що можна виділити такі 3 команди, які б виграли у решти. 
Вказівки

1)  зустріч, 91 бал.

2) Команда Г (І місце) виграла більше половини з 13 зустрічей (щонайменше 7). Якби команда Г ви­грала 6 зустрічей, то 6 • 14 = 84 (бали), що менше за 
91 бал (суперечність).

3) 14 = 1 (Г) + 7 (ті, що програли Г) + 6 (ко­манд).

4) Виберіть три команди А, Б, В серед шести команд, що залишилися. Обґрунтуйте свій вибір.

5) Четвірка команд А, Б, В, Г задовольняє умову задачі.

 

 

 

 

 

 

 

 

 

Висновки

    Працюючи по будь-якому підручнику, вчитель може проявляти творчий підхід до навчання учнів, удосконалювати освітній процес, навчати мислити. Необхідно систематично використовувати на уроках завдання, сприяючі формуванню в учнів пізнавального інтересу і спостережливості. Здійснюючи цілеспрямоване навчання школярів розв'язанню задач, за допомогою спеціально підібраних вправ, навчити їх спостерігати, користуватися аналогією, індукцією, порівняннями і робити відповідні висновки.

    Логічне мислення розвивається інтенсивніше, якщо створювати на уроках атмосферу пошани, заохочувати ініціативу і стимулювати творчість учнів. Системний розвиток логічного мислення має бути невідривно від уроку, кожен учень повинен брати участь в процесі розв'язання не лише стандартних завдань, але і завдань розвиваючого характеру (активно або пасивно).

     Істотно важливо, щоб вчитель математики, шкільний підручник, демонстрували справжні зразки культури мислення. Адже  учні в своїй розумовій діяльності природно наслідують вчителеві, підручнику. І якщо вчитель припускається похибок в логічному викладання, в обґрунтуванні, то звичайно, важко чекати від учнів високої культури мислення.

            Підбиваючи підсумки, хотілося б навести ще один вагомий аргумент на користь необхідності найактивнішого використання нестандартних задач в навчальному процесі. Подивіться в очі учнів, які виходять з  уроку з використанням таких задач, і очі учителя. Ці люди отримали радість від спільної праці. Що тоді щастя, якщо не це?!

 

 

 

 

 

 

 

Список використаних джерел

 

1.Автомонов П. Т. Оптимальна технологія навчання: [ метод. посібник] /   

П. Т. Автомонов, О. О. Автомонова. – К., 1996. – 71с.

2.Андреєва В.М. Настільна книга педагога / В. М .Андреєва,

В. В. Григораш. - / Х.: Вид. група « Основа», 2009.-352с.

3.Аніпонова М.. Активізація творчої діяльності учнів на уроках математики. // Математика. – 2009. – Червень. № 23. – С. 3–6..

4.Барташнікова І. А., Барташніков О. О. Розвиток уяви та творчих здібностей у дітей - Тернопіль, "Богдан", 1998

5.Гальперин П. Я. Введение в психологию. / П. Я.Гальперин. - Москва: 1976. – 120с.

6. Давыдов В. В. Психическое развитие в младшем школьном возрасте   / под ред. А. В. Петровского. – М.: Педагогика, 2001. – 167с.

7.  Демиденко В.К. Виховання інтересу в учнів до навчання. – К.: Знання, 1978. – 183ст.

8.Дичківська І.М. Інноваційні педагогічні технології. – К.: Академвидав,  2004. – 351 с.

9. Друзь Б. Математична мозаїка. К.: Веселка, 1991. - 130 с.

10.Дудач І. Активізація мислення учнів за допомогою інтерактивних технологій навчання. // Математика в школах України. – 2007. – № 33.– С. 8–11.

11.Ивин А. А. Логика. – М.: Просвещение,1996. – 206 с

12.Игнатьев Е. И. Математическая смекалка. – М.: Омега, 1994.

13. Забранська Н. Активізація пізнавальної діяльності учнів на уроках математики. // Математика. – 2004. – серпень № 31– 32. – С. 13–15.

14.Енциклопедія педагогічних технологій та інновацій / автор – укладач  Н.П. Наволокова. – Х.: Вид. група «Основа», 2009. – 176 с.

15.Киричук О.І. Виховання в учнів інтересу до навчання. – К.,1986 – 89ст.

16.Как проектировать универсальные учебные действия в начальной школе. От действия к мысли. – Москва: Просвещение, 2010 - с 28, 30, 91

17. Математика. 5 кл. : підруч. для закладів загальної середньої освіти /

Н. А. Тарасенкова, І. М. Богатирьова, О. П. Бочко, О. М. Коломієць, З. О. Сердюк. —Вид. 2-ге, доопр. — К. : Видавничий дім «Освіта», 2018. — 240 с.

18. Математика. 6 кл. : підруч. для закладів загальної середньої освіти /

Н. А. Тарасенкова, І. М. Богатирьова, О. М. Коломієць, З. О. Сердюк. —К. : Видавничий дім «Освіта», 2014. — 304 с.

19. Математичні розминки в 5 – 6  класах: Посібник. - Творча група «Гармонія» Решетилівської ЗОШ І-ІІ ступенів, 2006. –  23 с.

20.Монот Л.Я. Передовий педагогічний досвід: теорія і методика. – К.:

радянська школа, 1990. – 141 с.

21.Пиаже Ж. Логика и психология. Избранные психологические труды. — М., 1969.

22.Рубинштейн С. А. Основы общей психологии: В 2т. – М.: Педагогика, 1989.– Т.2– 328с.

23. Сойер У. У. Прелюдия к математике. М.: Просвещение, 196с

24. Столяр А. А. Педагогика математики. – Минск, Высшая школа,1986.

25. http://www.kangaroo.com.ua/index.php?r=pages/view&alias=archive