Розвиток тригонометрії у стародавній Греції та Індії

В.Е. Цоуфал

УДК 514.116(09)

Розвиток тригонометрії у Стародавній Греції та Індії

 У статті висвітлено шляхи розвитку тригонометрії в Стародавній Греції та Індії, розкрито внесок видатних науковців в розвиток плоскої та сферичної тригонометрії та значення для подальшого розвитку цієї галузі математичних знань.

 Ключові слова: тригонометрія, історія тригонометрії, видатні математики Стародавньої Греції та Індії.

 The article describes the ways of the development of trigonometry in Ancient Greece and India, reveals the contribution of outstanding scientists to the development of plane and spherical trigonometry and importance for the further development of this field of mathematical knowledge.

 Keywords: trigonometry, the history of trigonometry, the outstanding mathematicians of Ancient Greece and India.

Постановка проблеми. Вивчення тригонометрії в старшій школі відіграє важливу роль у системі математичної освіти, оскільки універсальність математичних методів дозволяє в формальних поняттях алгебри, геометрії та математичного аналізу на рівні загальнонаукової методології відобразити зв’язок теоретичного матеріалу з різних галузей знань з практичною діяльністю.

Тригонометрія як галузь наукового знання має багату й цікаву історію, яка налічує не одне тисячоліття. Тригонометрія виникла в стародавні часи як один із розділів астрономії і в своєму розвитку пройшла кілька етапів, перш ніж набула сучасного вигляду. Кожен етап цього розвитку вирізняється своїми особливостями, науковими пошуками та здобутками, іменами провідних науковців, які зробили вагомий внесок у формування тригонометрії як науки.

Аналіз досліджень. Вивчення наукової літератури дозволяє говорити, що різними аспектами методики навчання тригонометричного матеріалу в школі займалися відомі науковці-математики, методисти: В. Брадіс, Н. Віленкін, Л. Люстерник, А. Мерзляк, О. Мордкович, С. Новосьолов, В. Рєп’єв, М. Рибкін, М. І. Шкіль, Н. М. Шунда та інші. Історії тригонометрії присвятили свої роботи Г. Вілейтнер, Г. Глейзер, К. Рибников, Г. Цейтен та інші дослідники.

Мета полягає в тому, щоб розкрити шляхи розвитку «тригонометрії» як науки в Стародавній Греції та Індії, показати важливість знання історії питання для дослідження на сучасному етапі.

Відповідно до поставленої мети можна виділити такі завдання:

1. Виділити хронологію розвитку «тригонометрії» в Стародавній Греції та Індії

2. Ознайомитись із внеском найвідоміших науковців в розвиток теорії тригонометричної.      

Виклад основного матеріалу.

Зародки тригонометрії можна знайти в математичних рукописах стародавнього Єгипту, Вавилона і стародавнього Китаю. 56-а задача з папірусу Рінда (II тисячоліття до н. е.) пропонує знайти нахил піраміди, висота якої дорівнює 250 ліктів, а довжина сторони основи — 360 ліктів.

Від вавилонської математики бере початок звичайне для нас вимірювання кутів градусами, мінутами і секундами (введення цих одиниць у давньогрецьку математику зазвичай приписують Гіпсиклу, II століття до н. е.) Серед теорем, відомих вавилонцям, була, приміром, така: вписаний кут, що спирається на діаметр кола — прямий. Головним досягненням цього періоду стало співвідношення, яке згодом отримало назву теореми Піфагора; Ван дер Варден вважає, що вавилонці відкрили його між 2000 і 1786 роками до н. е. Цілком можливо, що китайці відкрили його незалежно (див. «Математика в дев'яти книгах»). Незрозуміло, чи знали загальне формулювання теореми стародавні єгиптяни, однак прямокутний «єгипетський трикутник» зі сторонами 3, 4, і 5 був там добре відомий і широко використовувався.

Стародавня Греція

Загальне і логічно зв'язне викладення тригонометричних співвідношень з'явилося в давньогрецькій геометрії. Грецькі математики ще не виділяли тригонометрію як окрему науку, для них вона буда частиною астрономії.[1]

Плоска тригонометрія

Декілька теорем тригонометричного характеру містять «Начала» Евкліда (IV століття до н. е.). В першій книзі «Начал» теореми 18 і 19 встановлюють, що більшій стороні трикутника відповідає більший протилежний кут — і навпаки, більшому куту відповідає більша сторона. Теореми 20 і 22 формулюють «нерівність трикутника»: з трьох відрізків можна скласти трикутник тоді і тільки тоді, коли довжина кожного менше суми довжин двох інших. Теорема 32 доводить, що сума кутів трикутника дорівнює 180°.[3]

У другій книзі «Начал» теорема 12 являє собою словесний аналог теореми косинусів:

В тупокутних трикутниках квадрат на стороні, що стягує тупий кут, більше (суми) квадратів на сторонах, що містять тупий кут, на двічі взятий прямокутник, поміщений між однією зі сторін при тупому куті, на яку спадає перпендикуляр, і відрізком при тупому куті, який відтинає цей перпендикуляр ззовні.

Наступна теорема 13 є варіантом теореми косинусів для гострокутних трикутників. Аналогу теореми синусів у греків не було, це найважливіше відкриття було зроблене значно пізніше.[2]

Подальший розвиток тригонометрії пов'язаний з ім'ям астронома Аристарха Самоського (III століття до н. е.). В його трактаті «Про величини і відстані Сонця і Місяця» була поставлена задача про визначення відстаней до небесних тіл; ця задача потребувала обчислення співвідношення сторін прямокутного трикутника при відомому значенні одного з кутів. Аристарх розглядав прямокутний трикутник, утворений Сонцем, Місяцем і Землею під час квадратури. Йому було потрібно обчислити величину гіпотенузи (відстань від Землі до Сонця) через катет (відстань від Землі до Місяця) при відомому значенні прилеглого кута (87°), що є еквівалентом обчислення значення   sin3∘. За оцінкою Аристарха, ця величина лежить у проміжку від 1/20 до 1/18, тобто відстань до сонця у 20 разів більше, ніж до Місяця; насправді Сонце знаходиться майже у 400 разі далі, ніж Місяць, помилка виникла через неточність у вимірюванні кута. Водночас Аристарх довів нерівність, яка у сучасних термінах передається формулою:

Ця ж нерівність міститься в «Обчисленні піщинок» Архімеда. В працях Архімеда (III століття до н. е.) наводиться важлива теорема ділення хорд, яка по суті еквівалентна формулі синуса половинного кута:

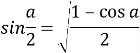
Греки також вирішили проблему побудови трикутника за його трьома заданими елементами (з яких хоча б один є стороною).

Протягом всього періоду розвитку античної науки головною нивою для застосування результатів плоскої тригонометрії у греків залишалась астрономія. Окрім задачі з обчислення відстаней, тригонометрію залучали для визначення параметрів системи епіциклів і/чи ексцентрів, якими представляли рух світила у просторі. За широко поширеною думкою, ця проблема вперше була сформульована Гіппархом (середина II століття до н. е.) при визначенні елементів орбіт Сонця і Місяця; можливо, аналогічними задачами займалися й астрономи більш раннього часу. Гіппарху також часто приписують авторство перших тригонометричних таблиць, які не збереглися. Втім, згідно з деякими реконструкціями, перші тригонометричні таблиці були складені ще у III столітті до н. е., можливо, Апполонієм Перзьким.

Замість сучасної функції синуса Гіппарх та інші давньогрецькі математики звичайно розглядали залежність довжини хорди кола від заданого центрального кута (чи, що еквівалентно, від заданої дуги кола, вираженої у кутовій мірі). У сучасній термінології, довжина хорди, що стягує дугу θ одиничного кола дорівнює подвоєному синусу центрального кута θ/2. Ця відповідність справедлива для будь-яких кутів: 0° < θ < 360°. Мовою хорд були сформульовані перші відкриті греками тригонометричні співвідношення. Наприклад, сучасній формулі:

у греків відповідала теорема:

де c h o r d α {\displaystyle chord_{\alpha }}  — хорда для центрального кута α {\displaystyle \alpha } , a, dd {\displaystyle d}  — діаметр кола.

При цьому радіус кола не вважався рівним одиниці, як тепер. Припускають, наприклад, що у Гіппарха радіус кола вважався рівним R=3438 одиниць — за такого визначення довжина дуги кола була рівною кутовій мірі цієї дуги, вираженої в мінутах:

і це полегшувало обчислення. У Птолемея R=60 одиниць. Згідно з сучасними реконструкціями, величини хорд у Гіппарха були протабульовані з інтервалом 7°30'. Можливо, в основі обчислення таблиці Гіппарха лежав метод, що був розроблений Архімедом і брав початок ще у Аристарха.

Пізніше астроном II століття Клавдій Птолемей в «Альмагесті» доповнив результати Гіппарха. Тринадцять книг «Альмагеста» — найзначніша тригонометрична робота всієї античності. Зокрема, «Амальгест» містить великі п'ятизначні таблиці хорд для гострих і тупих кутів з кроком 30 кутових мінут. Для обчислення хорд Птолемей використовував (у главі X) теорему Птолемея (втім, відому ще Архімеду), яка стверджує: сума добутків довжин протилежних сторін випуклого вписаного в коло чотирикутника дорівнює добутку довжин його діагоналей. З цієї теореми нескладно вивести дві формули для синуса і косинуса суми кутів і ще дві для синуса і косинуса різниці кутів, проте загальне формулювання цих теорем у греків відсутнє.

Основним досягненням античної тригонометричної теорії став розв'язок у загальному вигляді задачі «розв'язування трикутників», тобто заходження невідомих елементів трикутника, коли відомі його три елементи (з яких хоча б одним є стороною). Пізніше ця задача і її узагальнення стали основною задачею тригонометрії: задані декілька (звичайно три) відомих елементи трикутника, вимагається знайти решту пов'язаних з ними величин. Спершу до числа елементів трикутника (відомих і невідомих) включали сторони і кути при їх вершинах, пізніше до них додались медіани, висоти, бісектриси, радіус вписаного і описаного кола, розташування центру ваги тощо. Прикладні тригонометричні задачі відрізняються великою різноманітністю — наприклад, можуть бути задані невидимі на практиці результаті дій над перерахованими величинами (приміром, сума кутів чи відношення довжин сторін).[4]

Сферична тригонометрія

Паралельно з розвитком тригонометрії площини греки, під впливом астрономії, значно розвинули сферичну тригонометрію. В «Началах» Евкліда з цієї теми є тільки одна теорема про співвідношення об'ємів шарів різного діаметра, але потреби астрономії і картографії зумовили швидкий розвиток сферичної тригонометрії і суміжних з нею областей — системи небесних координат, теорії картографічних проекцій, технології астрономічних приладів (зокрема, була винайдена астролябія).

Історики дійшли згоди щодо ступеню розвитку у античних греків геометрії небесної сфери. Деякі дослідники наводять аргументи, що екліптичну чи екваторіальну систему координат використовували для запису результатів астрономічних спостережень принаймні вже у час Гіппарха. Можливо тоді були відомі і деякі теореми сферичної тригонометрії, які могли використовуватись для складення зоряних каталогів і в геодезії.

Перші відомі в наш час праці зі «Сферики» (тобто сферичної геометрії, з очевидним астрономічним нахилом) написали:

    (IV століття до н. е.) Автолік з Пітани і Евклід («Феномени»).

    (II століття до н. е.) Феодосій і Гіпсикл.

Деякі задачі розглянуті в цих творах мають тригонометричний характер, проте через слабку розробленість теорії автори ще користуються обхідними шляхами. Наприклад, задачу «знайти час повного сходу (заходу) зодіакального сузір'я» Гіпсикл вирішує наближено за допомогою многокутних чисел.

Вирішальним етапом в розвитку теорії стала монографія «Сферика» в трьох книгах, яку написав Менелай Александрійський (близько 100 року н. е.). В першій книзі він виклав теореми про сферичні трикутники, аналогічні теоремам Евкліда про плоскі трикутники. Історики вважають, що підхід Менелая багато в чому спирається на праці Феодосія, які у Менелая суттєво розширені і зведені в систему. Як повідомляє Паппа, Менелай першим ввів поняття сферичного трикутника як фігури, утвореної відрізками великих кіл. Менелай довів теорему, для якої у Евкліда немає плоского аналога: два сферичних трикутники конгруентні (сумісні), якщо відповідні кути рівні. Інша його теорема стверджує, що сума кутів сферичного трикутника завжди більше 180°.

Друга книга «Сферики» викладає застосовування сферичної тригонометрії до астрономії. Третя книга місить важливу для практичної астрономії теорему Менелая, відому як «правило шести величин». Дві інші відкриті Менелаєм фундаментальні теореми пізніше отримали назви «правило чотирьох величин» і «правило тангенсів».

Кілька десятиліть потому Клавдій Птолемей у своїх працях «Географія», «Аналемма» і «Планісферій» приводить докладне викладення застосування тригонометрії до картографії, астрономії і механіки. Серед іншого, описана стереографічна проекція, досліджені кілька практичних задач, наприклад: визначити висоту і азимут небесного світила за його схиленням і часовим кутом. З точки зору тригонометрії, це означає, що потрібно знайти сторону сферичного трикутника за двома іншими сторонами і протилежним кутом.

Сферичній геометрії Птолемей також присвятив XIII главу в першій книзі «Амельгеста»; на відміну від Менелая, Птолемей не привів доведень багатьох тверджень, але натомість приділив багато уваги алгоритмам, придатним для практичних обчислень в астрономії. Опорною конструкцією в «Амальгесті» слугує, замість плоских хорд, «чотиристоронник Менелая». Для вирішення прямокутного сферичного трикутника, тобто для обчислення його характеристик, Птолемей навів у словесній формі 4 теореми; в сучасних позначеннях вони мають вигляд (кут C прямий):

sin a=sin c*sin A (окремий випадок сферичної теореми синусів)

tg a=sin b*tg A

cos  c = cos  a ⋅ cos b (окремий випадок сферичної теореми синусів)

tg b = tg c ⋅ cos A

Пояснимо, що в сферичній геометрії прийнято вимірювати сторони трикутника не лінійними одиницями, а величиною центральних кутів, що на них спираються. В сучасній сферичній геометрії наводяться ще два співвідношення:

cos A=cos a*sin B (також виходить з сферичної теореми косинусів)

cos  c = ctg  A ⋅ ctg  B

У Птолемея вони відсутні, оскільки їх неможливо вивести з теореми Менелая.

Індія

У IV столітті, після занепаду античної науки, центр розвитку математики змістився до Індії. Твори індійських математиків (сіддханти) демонструють, що їх автори були добре знайомі з працями грецьких астрономів і геометрів. Чистою геометрією індійці цікавились мало, але їх внесок в прикладну астрономію і розрахункові аспекти тригонометрії дуже значний.

В першу чергу індійці змінили деякі концепції тригонометрії, наблизивши їх до сучасних. Вони провели заміну античних хорд на синуси (назва синус походить від слова тятива на санскриті) в прямокутному трикутнику. Тим самим в Індії була започаткована тригонометрія як загальне вчення про співвідношення у трикутнику, хоча, на відміну від грецьких хорд, індійський підхід обмежувався тільки функціями гострого кута.

Синус індійці визначали інакше, ніж в сучасній математиці: під синусом розуміли довжину відрізку AD, що спирався на дугу AC кола з радіусом R=3438 одиниць (як у Гіппарха). Таким чином, «індійський синус» кута у 3438 разів більше сучасного синуса і мав розмірність довжини. З цього правила були винятки: наприклад, Брамагупта з неясних причин узяв радіус рівний 3270 одиниць.[5]

Індійці першими ввели у використання косинус. Використовувався ще так званий обернений синус, чи синус-верзус, рівний довжині відрізку DC на малюнку праворуч.

Як у греків, тригонометрія індійців розвивалася головним чином у зв'язку з її астрономічним застосуванням, в основному для використання в теорії руху планет і для вивчення небесної сфери. Це свідчить про добре знання сферичної тригонометрії «Амальгеста» і «Аналемми», однак жодної їх власної роботи, яка б розвивала теорію цього розділу тригонометрії, не виявлено. Тим не менш в розробленні прикладних алгоритмів вирішення астрономічних задач індійці досягнули великих успіхів. Наприклад, в «Панча-сіддхантиці» Варахаміхіри (VII століття) наводиться оригінальне вирішення астрономічної задачі, описаної у Птолемея: знайти висоту сонця над горизонтом, якщо відомі широта місцевості, схилення Сонця і його часовий кут. Для вирішення автор застосовує аналог теореми косинусів, він також вперше навів формулу для синуса половинного кута.

Для астрономічних розрахунків був складений ряд тригонометричних таблиць. Перші (чотиризначні) таблиці синусів наведені в стародавній «Сурья-сіддханті» і у Аріабхати («Аріабхатія», V століття). Таблиці Аріабхати містять 24 значення синусів і синус-верзусів з інтервалом 3°45' (половина кроку таблиць у Гіппарха).[2]

Важливий внесок в розвиток тригонометрії зробив Брахмагупта (VII століття), який відкрив декілька тригонометричних співвідношень, зокрема й ті, що в сучасному запису набули вигляду:

Крім того, індійці знали формули для кратних кутів sin  n φ, cos n φ для n = 2 , 3 , 4 , 5. В «Сурья-сіддханті» і в працях Брахмагупти при вирішенні задач фактично використовується сферичний варіант теореми синусів, однак загальне формулювання цієї теореми в Індії так і не з'явилось. Історики виявили в індійських працях неявне використання тангенсів, але важливість цього поняття була усвідомлена тільки пізніше, математиками ісламських країн.

В працях іншого видатного ученого, Бхаскари II (XII століття), наведені формули для синуса і косинуса суми і різниці кутів:

sin ( α ± β ) = sin  α cos β ± cos α sin  β ,

а також формула для малого приросту синуса:

    sin α − sin β ≈ ( α − β ) cos  β (при α ≈ β) відповідна сучасному виразу для диференціалу синуса. Спираючись на формулу синуса суми, Бхаскара опублікував більш точні і докладні, ніж у Аріабзати, тригонометричні таблиці з кроком 1°.[4]

У XI столітті мусульмани (Махмуд Газневі) захопили і спустошили Північну Індію. Культурні центри перемістилися до Південної Індії, де сформувалася так звана школа «Керала» (за назвою сучасного штату Керала на півдні Індії). У XV–XVI століттях математики Керали під час астрономічних досліджень досягли великих успіхів в області сумування нескінченних числових рядів, в тому числі для тригонометричних функцій. В анонімному трактаті «Каранападдхаті» («Техніка обчислення») наведені правила розкладання синуса і косинуса на нескінченні ступеневі ряди, що вірогідно брали початок від засновника цієї школи астронома Мадхава (1 пол. XV століття). Мадхава і його послідовник Нілаканта (у трактаті «Тантрасанраха») наводять також правила розкладання арктангенса в нескінечний ступеневий ряд. В Європі до подібних результатів дійшли лише у XVII–XVIII століттях. Так, ряди для синуса і косинуса вивів Ісаак Ньютон близько 1666 року, а ряд арктангенса був знайдений Дж. Грегорі у 1671 році і Ґ. В. Лейбніцем у 1673 році.[5]

Висновки. Вивчення історичних відомостей з тригонометрії сприяє збагаченню наукового світогляду учнів, закріпленню та розвитку інтересу до математики, інтеграції математичних і гуманітарних знань.

Список використаних джерел

1.    Бевз Г. П. Методи навчання математики / Г. П. Бевз // Математика в школах України: Наук.-теорет. і метод. журнал. – Харків : Основа, 2003. – 96 с.
2.    Вилейтнер Г. История математики от Декарта до середины XIX столетия / Г. Вилейтнер. – М.: Изд-во физ.-мат. лит., 1960. – 467 с.
3.    Глейзер Г. И. История математики в школе. IX-X классы : пособие для учителей / Г. И. Глейзер. – М. : Просвещение, 1983. – 350 с.
4.    История математики: В 3 т. – Т. 1. С древнейших времен до начала нового времени / под ред. А. П. Юшкевича. – М.: Наука, 1970. – 350 с.
5.    Слєпкань З. І. Методика навчання математики / З. І. Слєпкань. – К. : Вища шк., 2006. – 582 с.