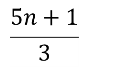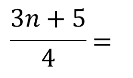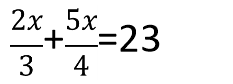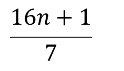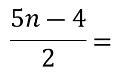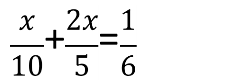Самостійна робота на тему: "Лінійне рівняння з однією змінною"

Рівняння з однією змінною

І ВАРІАНТ

Розв'язати рівняння:

1)     (x+3)(2x-5)=0

2)    5y-4(2y+3)=-6

3)   |2y-1|=2

5)

6) При якому значенні a рівняння  (5+a)x= 7-4a 

має корінь, що дорівнює 3?

ІІ ВАРІАНТ

Розв’язати рівняння:

1.   (2x-6)(x+2)=0

2.  40-5(3x-4)+4(x+18)=0

     3) |2y+3|=1

5)

6) При якому значенні a рівняння  (4a-1)x= 1+16a має корінь,

що дорівнює числу 4?