Самостійна робота з геометрії для 10 класу на тему "Теорема про три перпендикуляри"

Самостійна робота  в 10 класі (фізико-математичний профіль) до теми

“Перпендикуляр і похила. Теорема про три перпендикуляри”

                            І варіант

1.  О – точка перетину діагоналей ромба АВСD, АС= 40 см ,                                       

ВD = 30 см, KB =4cм  ().                                                                               

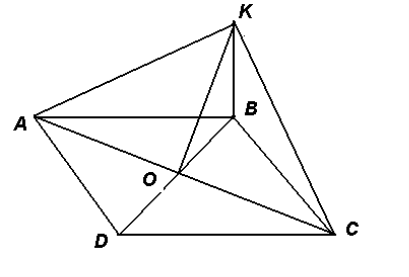
   Знайти:  1)довжину KO;                                                                                               

               2) сторону ромба  ABCD;                                                                              

               3) довжину відрізка  KC;                                                                               

               4) величину кута KOC;                                                                                                  

               5) площу трикутника  AKO;                                                                                     

               6) синус кута     KCO.                                                                                               

 2. Із точки до площини проведено дві похилі, довжини яких відносяться

     як 5: 6. Знайти відстань від точки до площини, якщо відповідні проекції

     похилих дорівнюють 4 см  і  см.

3. Через вершину прямого кута С прямокутного трикутника АВС до його

    площини проведено перпендикуляр СD, що дорівнює 1 дм. Знайти площу

    трикутника ADB, якщо АС = 3 дм, AD = 2 дм.

                                        ІІ варіант                                                                                               

     О – точка перетину діагоналей ромба АВСD, АС = 30 см ,                                    

ВD = 16 см,  FА = 16 cм  ()     

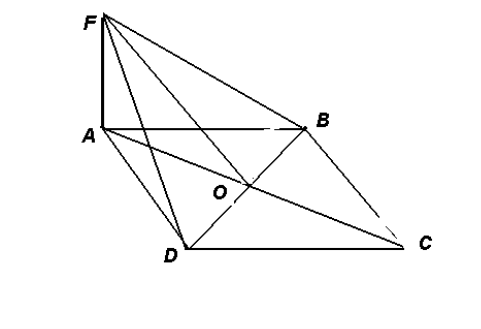
Знайти:  1)довжину FO;                                                                                               

               2) сторону ромба  ABCD;                                                                              

               3) довжину відрізка  FD;                                                                               

               4) величину кута FOB;                                                                                                  

               5) площу трикутника  AFO;                                                                                     

               6) синус кута     FCO.                                                                                               

2. Із точки до площини проведено дві похилі, різниця довжин яких дорівнює

    6 см. Їх проекції на цю площину дорівнюють 27 см і 15 см. Знайти відстань

     від даної точки до площини.

3. У прямокутному трикутнику АВС = 90°, АС = 6 см, ВС = 8 см, СМ- ме-

    діана. Через вершину С проведено пряму СК перпендикулярно до площини

    трикутника АВС, причому СК = 12 см. Знайти КМ.

             Використані джерела:

1.  Г.М. Литвиненко, Л.Я. Федченко, В.О. Швець, Збірник завдань для

     екзамену на атестат про середню освіту, Частина ІІ . Геометрія. 2-ге

     вид.,випр. – Львів: ВНТЛ., 1999.-  96с.