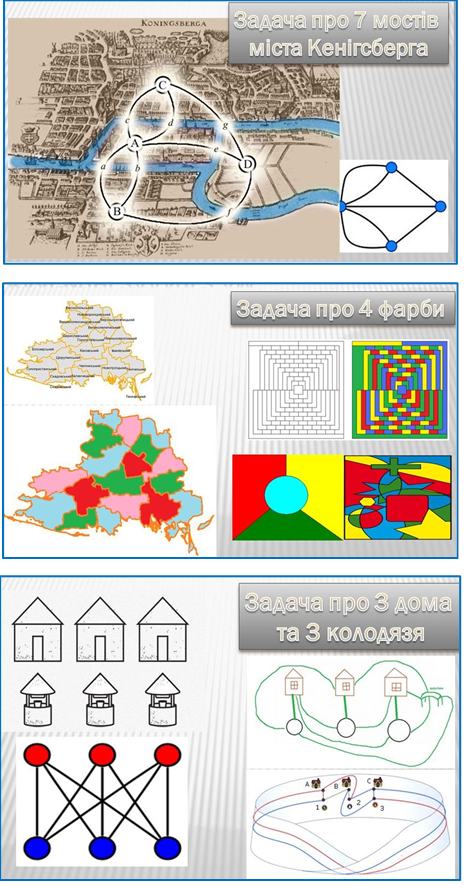
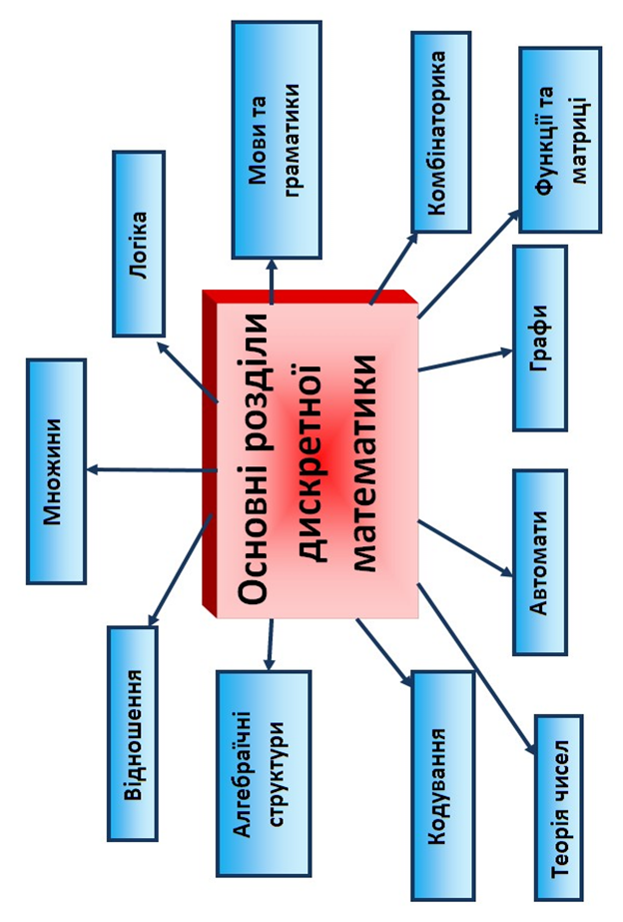
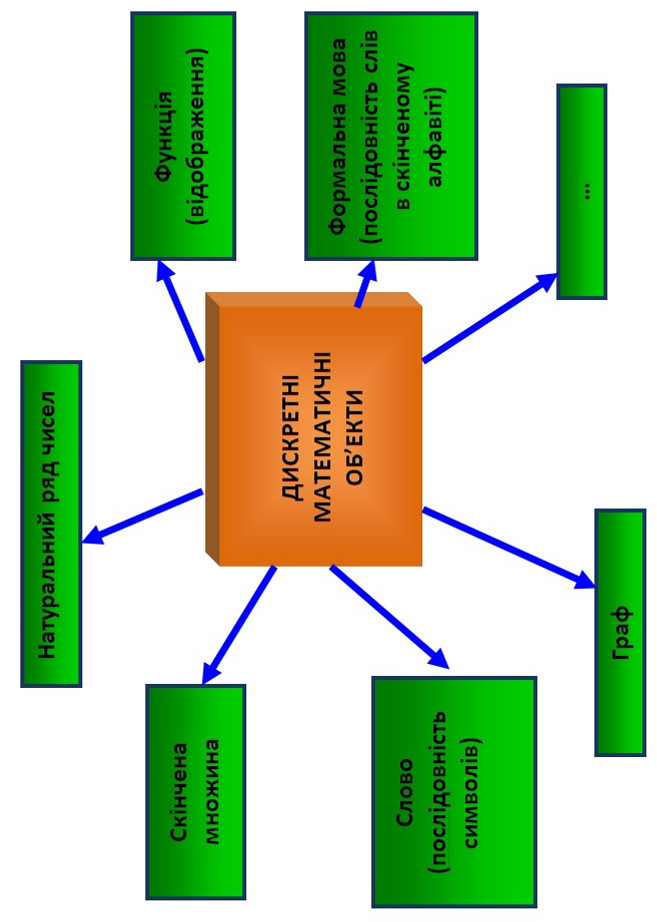
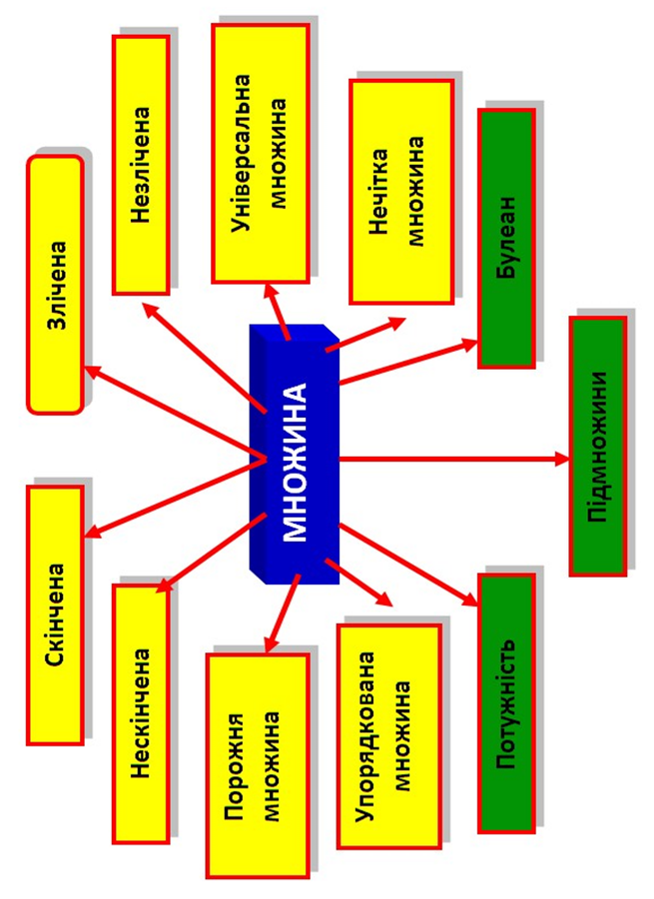
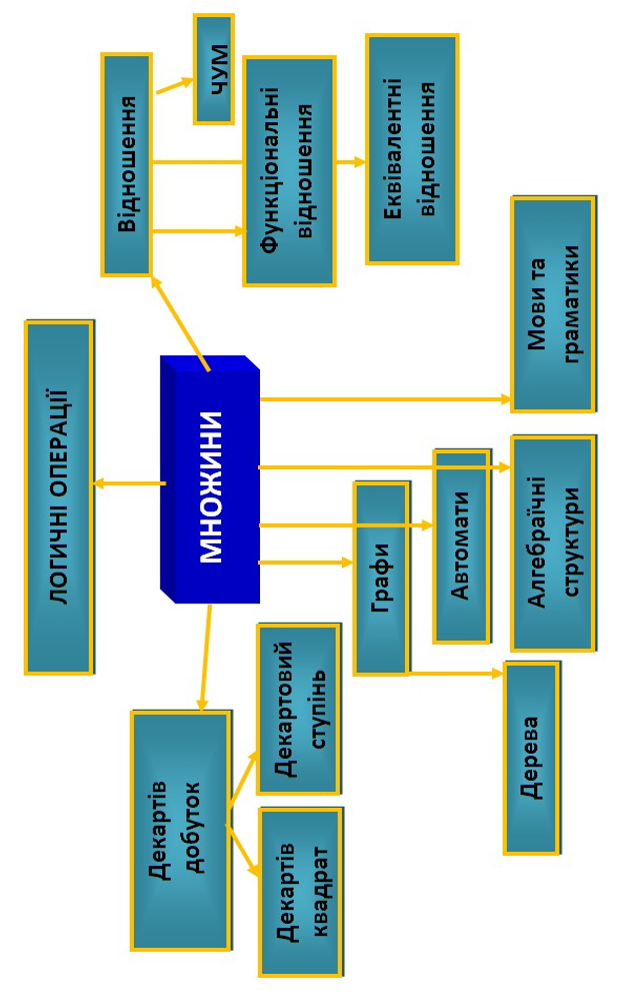
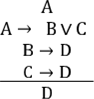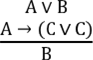Схеми з дисципліни "Дискретна математика"
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
Новокаховський приладобудівний технікум
м. Нова Каховка
2019
АНОТАЦІЯ
Посібник у схемах та таблицях з дисципліни «Дискретна математика» розроблений у відповідності до навчальної програми для студентів спеціальності 121 «Інженерія програмного забезпечення» галузі знань «Інформаційні технології» та може використовуватися як наочний матеріал на заняттях, як довідковий посібник, як слайдові - презентаційний матеріал до занять, як матеріал до фреймової методики навчання, та методичний матеріал для самостійного опрацювання студентами.
Використання викладачем і студентами опорних схем, таблиць дає можливість сформувати найважливіші сучасні вміння при вивченні дискретної математики – вміння кодувати великий об’єм інформації, будувати логічні ланцюжки для міркування, а отже засвоювати нові способи діяльності.
Запропоновані схеми та таблиці – засоби, які є згустком найнеобхіднішої інформації. Вони дають змогу вибудувати систему певного блоку розділу дискретної математики, полегшуючи одночасно розуміння його структури і сприяючи логічному впорядкуванню засвоєного матеріалу, що мотивує студента більш глибоко вивчати навчальну дисципліну.
ЗМІСТ
2 ВІДОМІ ВЧЕНІ, ЩО ДОСЛІДЖУВАЛИ ПРОБЛЕМИ ДИСКРЕТНОЇ МАТЕМАТИКИ................ 7
ВСТУП
Існує багато підручників, посібників, брошур, на просторах Інтернету велика кількість сайтів, які призначені для оволодіння знаннями з дискретної математики. В наш комп’ютеризований час знайти потрібну інформацію не важко. Проблема в тому – скільки часу ми витрачаємо на її пошук, обробку та представлення цієї інформації на заняттях.
В даному збірнику представлена сінгульована інформація в схемах і таблицях по ознайомленню з основними розділами дискретної математики. Авторська методика дозволяє використовувати матеріали збірника на всіх етапах заняття.
Мета цього посібника – допомогти викладачу дискретної математики із застосуванням новітніх технологій (наприклад, проектів, презентацій, опорних конспектів, фреймової методики, тощо). Всім викладачам відомо, що зорова та образна інформація сприяють якісному її засвоєнню та підвищують відсоток запам’ятовування.
Отже, завдання викладача, який працює із опорними схемами та таблицями, зводиться не тільки до того, щоб допомогти студентам створювати певні уявлення, але й щоб навчити їх мислити, порівнювати, міркувати, робити висновки, шукати правильне, ефективне рішення, тому що схеми є однією з найбільш доступних форм абстракції.
Рекомендується для застосування викладачам при викладанні дисципліни та студентам при її вивченні.
Бажаю успіхів!
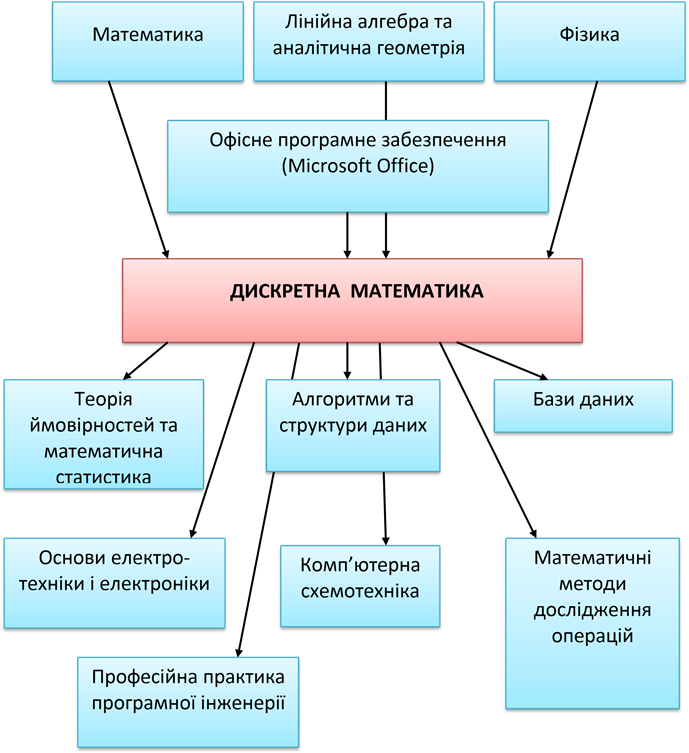
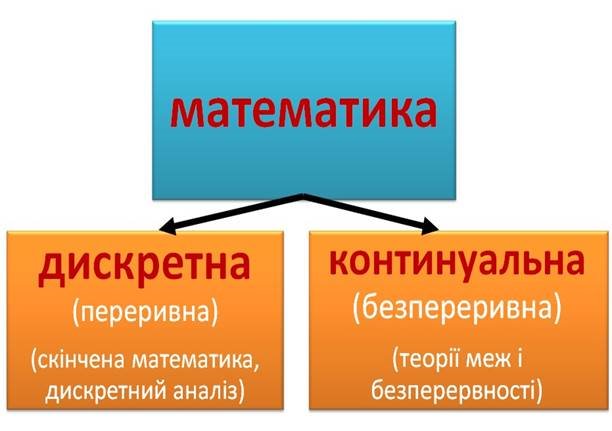
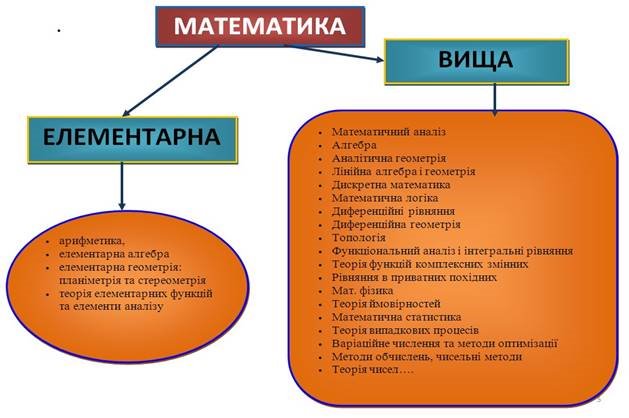
1 МІСЦЕ ДИСКРЕТНОЇ МАТЕМАТИКИ

Аристотель
384 до н. е.

Еміль Леон Пост
11 .02.1897— 21.04.1954

24.08.1923, — 30.01. 1982
МАТЕМАТИКИ




|
18.05.1872 — 2.02.1970 р.
|
23 .06 .1912 — 7 .06.1954
|
||
|
(молодший) 9 .09.1903 — 11.10.1979 |
22.07.1869— 28.03.1947
|
|
|

5 ТЕОРІЯ МАТЕМАТИЧНОЇ ЛОГІКИ ТА БУЛЕВОЇ АЛГЕБРИ
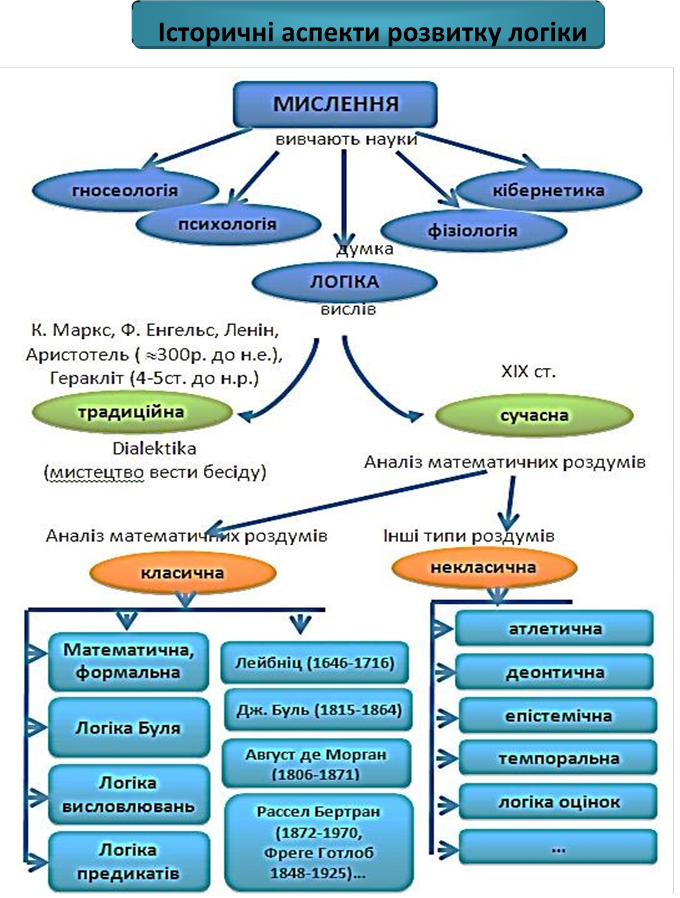
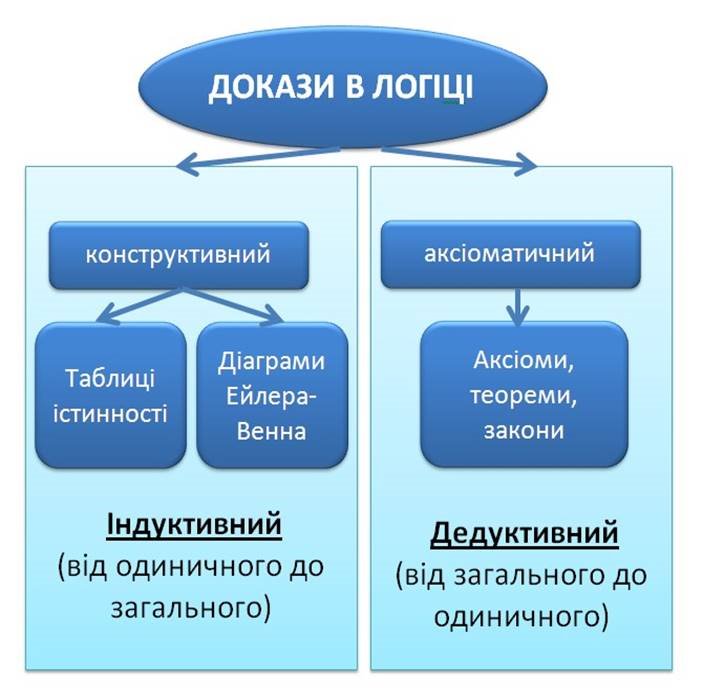
 Закони булевої алгебри
Закони булевої алгебри
|
1. Комутативність об’єднання
|
1’. Комутативність перерізу
|
|
2. Асоціативність
|
2’. Асоціативність
|
|
3. Дистрибутивність об’єднання відносно перерізу
|
3’. Дистрибутивність перерізу відносно об’єднання
|
|
4. Закони ї дії з порожньою та універсальною множинами
|
4’. Закони і дії ї порожньою та універсальною множинами
(протиріччя)
|
|
5. Закон ідемпотентності об’єднання |
5’. Закон ідемпотентності перерізу |
|
6. Закон де Моргана
|
6’. Закон де Моргана
|
|
7. Закон поглинання (елімінації)
|
7’. Закон поглинання (елімінації)
|
|
8. Закон склеювання
|
8’. Закон склеювання
|
|
9. Закон Порецького
|
9’. Закон Порецького
|
|
10. Закон подвійного доповнення (подвійного заперечення, інволюції) :
|
|
 Форми представлення булевих функцій
Форми представлення булевих функцій
|
a |
b |
|
0 |
0 |
|
0 |
1 |
|
1 |
0 |
|
1 |
1 |

18
 Основні логічні елементи
Основні логічні елементи
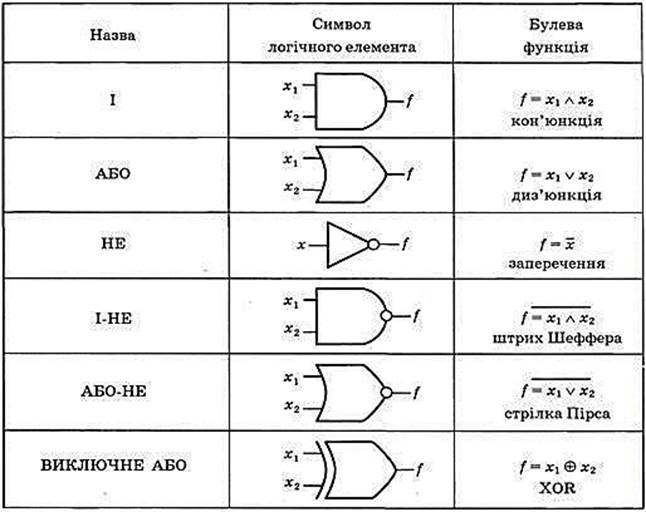
19
 Класи булевих функц ій
Класи булевих функц ій
|
№ |
код |
операція |
|
|
КЛАС |
|
|
|
Т0 |
Т1 |
S |
M |
L |
|||
|
0. |
0000 |
0
|
+ |
|
|
+ |
+ |
|
1. |
0001 |
|
+ |
+ |
|
+ |
|
|
2. |
0010 |
A-B
|
+ |
|
|
|
|
|
3. |
0011 |
A |
+ |
+ |
+ |
+ |
+ |
|
4. |
0100 |
B-A
|
+ |
|
|
|
|
|
5. |
0101 |
B |
+ |
+ |
+ |
+ |
+ |
|
6. |
0110 |
|
+ |
|
|
|
+ |
|
7. |
0111 |
|
+ |
+ |
|
+ |
|
|
8. |
1000 |
|
|
|
|
|
|
|
9. |
1001 |
|
|
+ |
|
|
+ |
|
10. |
1010 |
|
|
|
+ |
|
+ |
|
11. |
1011 |
|
|
+ |
|
|
|
|
12. |
1100 |
|
|
|
+ |
|
+ |
|
13. |
1101 |
|
|
+ |
|
|
|
|
14. |
1110 |
|
|
|
|
|
|
|
15. |
1111 |
1 |
|
+ |
|
+ |
+ |
6 ТЕОРІЯ ВІДНОШЕНЬ

 Відношення (відповідність)
Відношення (відповідність)
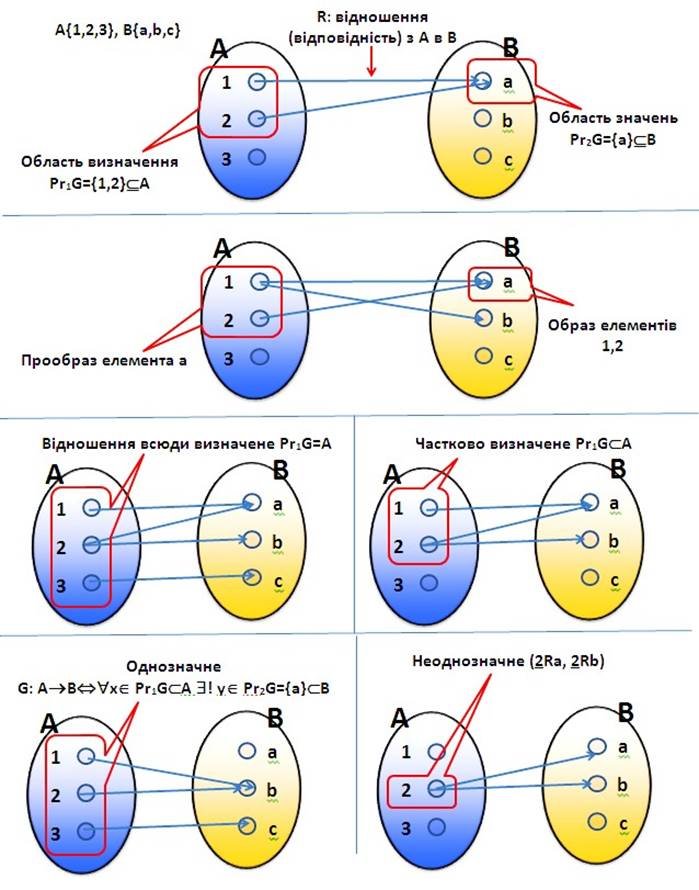
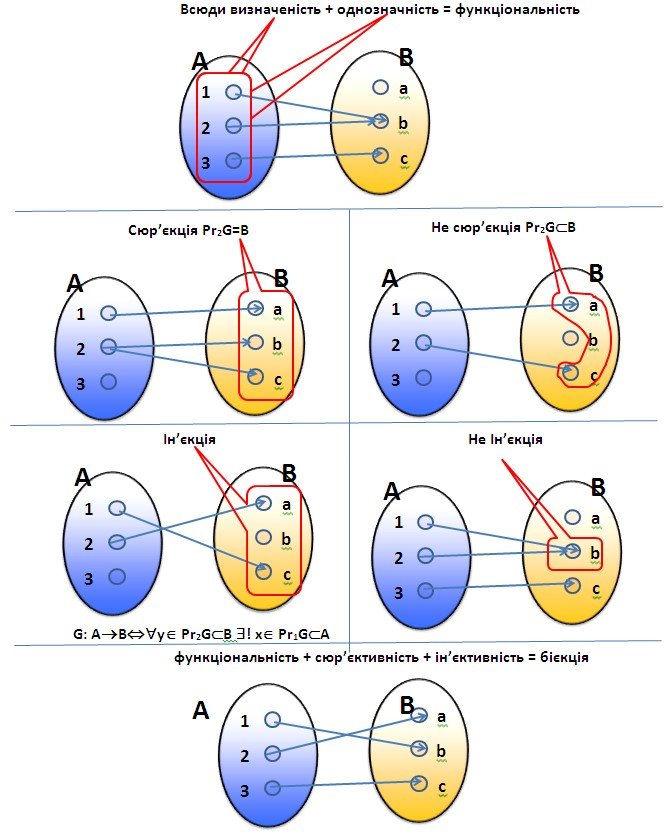
 Функціональні відношення
Функціональні відношення
7 ОСНОВНІ ФОРМУЛИ КОМБІНАТОРИКИ

8 ОСНОВНІ ПРАВИЛА ЛОГІКИ ВИСЛОВЛЮВАНЬ
 Правила дедуктивних висновків логіки висловлювань
Правила дедуктивних висновків логіки висловлювань
|
Правило дедуктивного висноску |
Тавтологія |
Назва правила |
|
|
|
А |
|
Правило введення диз’юнкції (розширення) |
|
|
|
|
Правило введення кон’юнкції |
|
|
|
|
Правило видалення диз’юнкції (Диз’юнктивний силогізм) |
|
|
|
|
Правило видалення кон’юнкції (спеціалізація) |
|
|
|
|
Правило котрапозиції імплікації |
|
|
|
|
Правило відділення (Modus Ponens) |
|
|
|
|
Від’ємна форма правила відділення (Modus Tollens) |
|
|
|
|
Гіпотетичний силогізм |
|
|
|
|
Вибір |
|
|
|
|
Виключний вибір |
|
|
|
|
Зведення до абсурду (Reductio ad Absurdum) |
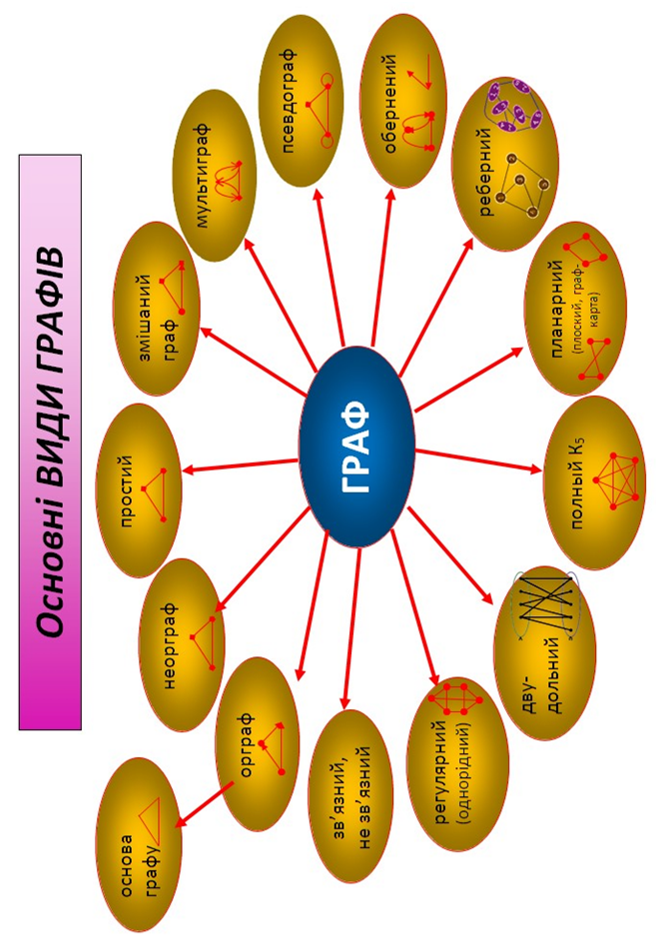
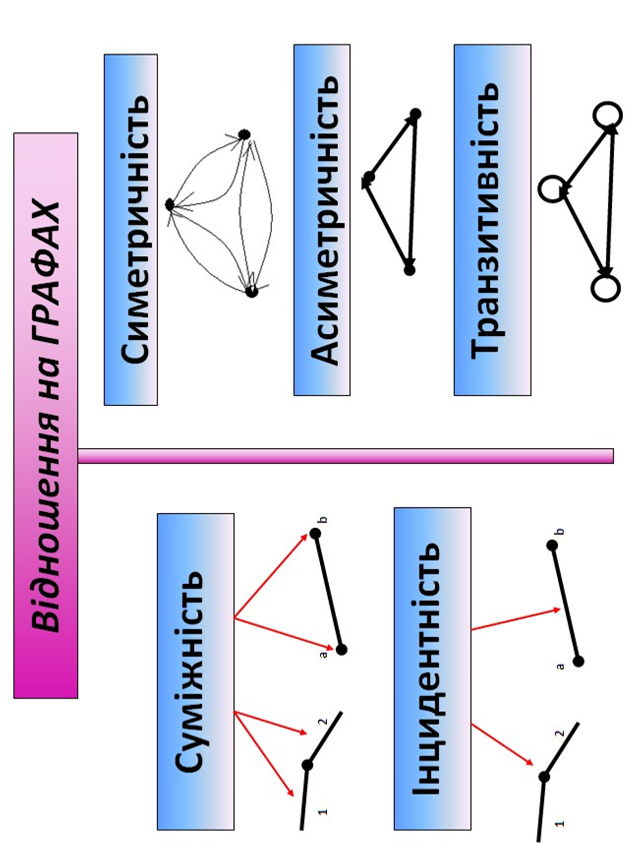
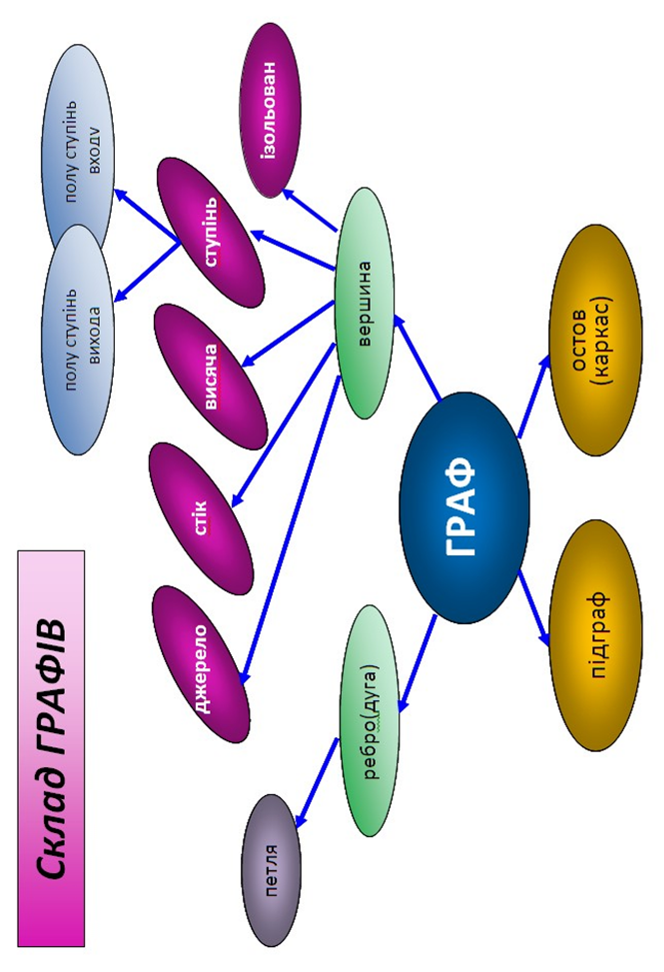
9 ТЕОРІЯ ГРАФІВ
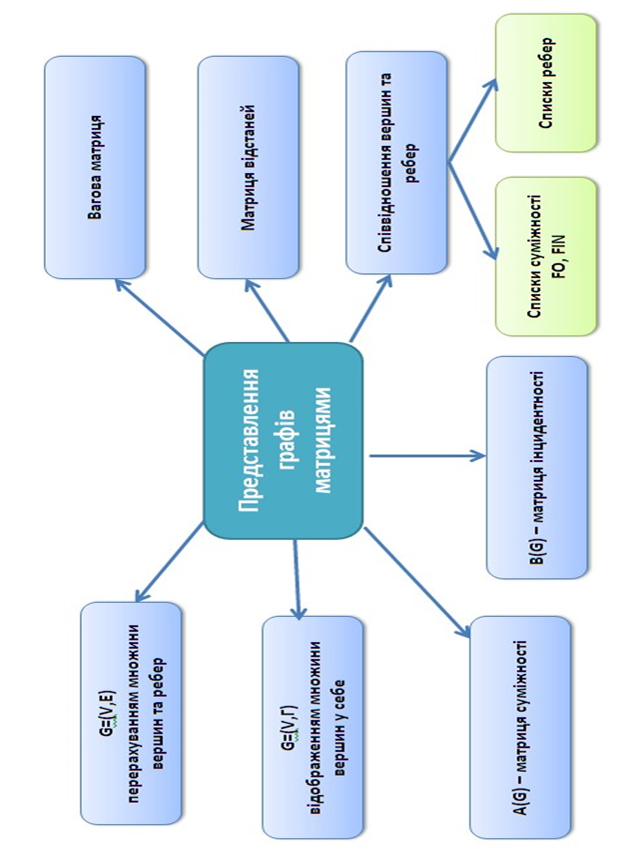
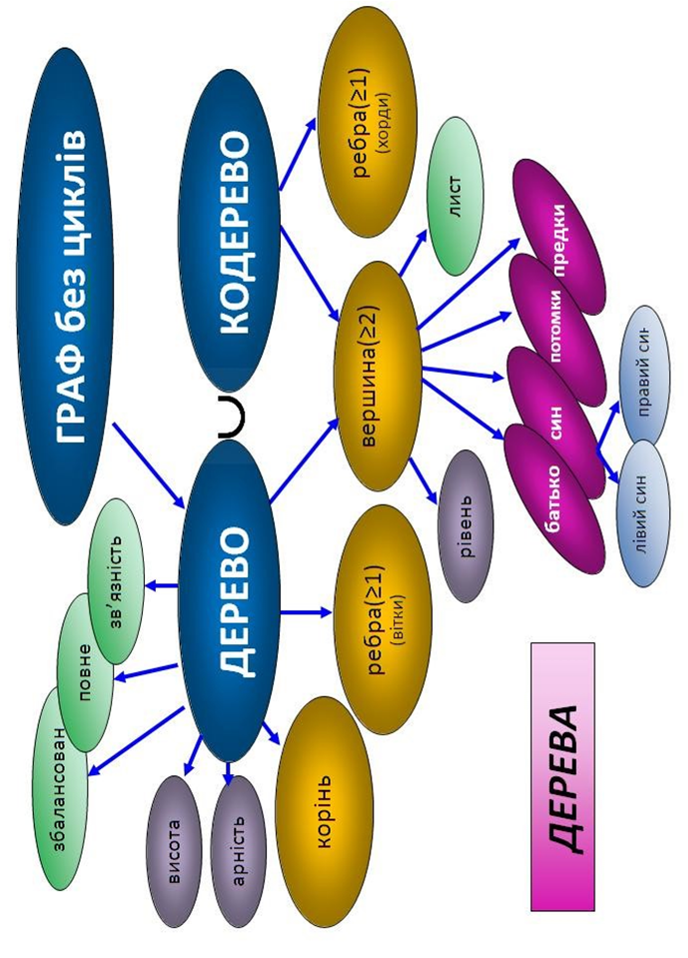
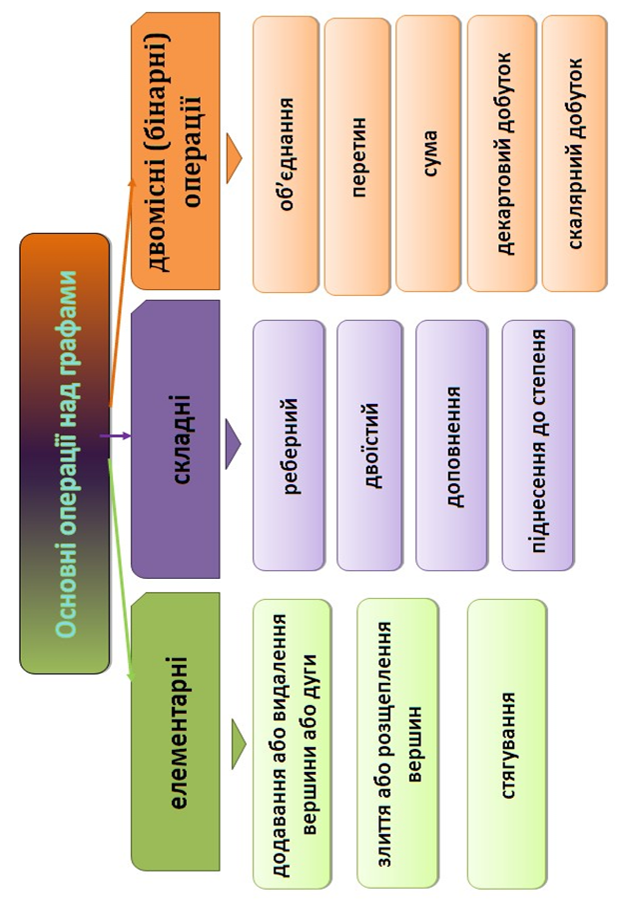
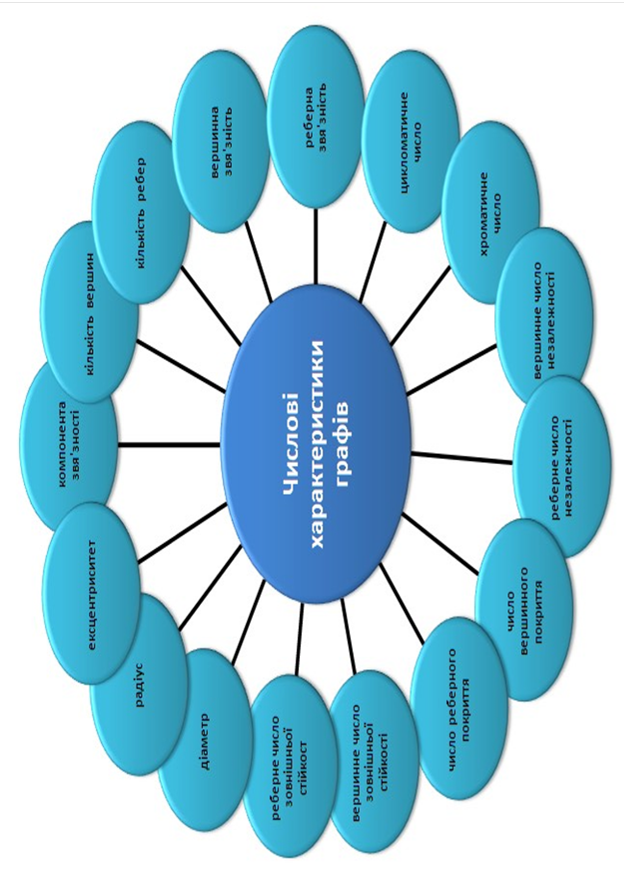
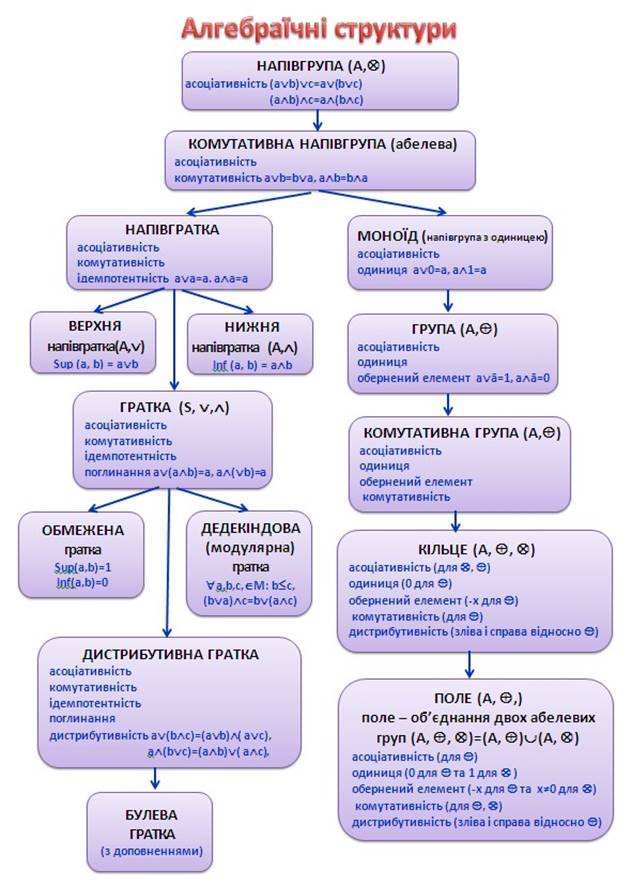
10 АЛГЕБРАЇЧНІ СТРУКТУРИ
СПИСОК ОСНОВНИХ ПОЗНАЧЕНЬ
![]() А-множина а А – елемент а належить множині А
А-множина а А – елемент а належить множині А
{a1,a2, …an} – множина елементів a1,a2, …an
{ а А |P}- множина елементів, які мають властивість Р
![]() А В - множина А є підмножиною множини В
А В - множина А є підмножиною множини В
- порожня множина
U - універсальна множина
![]() (А) – множина всіх підмножин множини А
(А) – множина всіх підмножин множини А
АхВ – декартовий добуток (а,b) - упорядкована пара
аRb – елемент a знаходиться у відношенні R до елемента b
![]() SR – композиція відношень
SR – композиція відношень
![]() (S, ≤) – множина S з відношенням часткового порядку f:A B - функція з множини А в множину В М(В, , , ) – Булева алгебра, де В={0, 1}
(S, ≤) – множина S з відношенням часткового порядку f:A B - функція з множини А в множину В М(В, , , ) – Булева алгебра, де В={0, 1}
![]() M(В, , , , , ) –алгебра логіки, де В={0, 1} M(В, , , 0, 1) –алгебра Жегалкіна, де В={0, 1} G(V, E) – граф з множиною V - вершин та Е –ребер deg(v) – степінь вершини v (A, ) (A,+) –верхня полугратка А
M(В, , , , , ) –алгебра логіки, де В={0, 1} M(В, , , 0, 1) –алгебра Жегалкіна, де В={0, 1} G(V, E) – граф з множиною V - вершин та Е –ребер deg(v) – степінь вершини v (A, ) (A,+) –верхня полугратка А
(A, ) (A, ) – нижня полугратка А
(S, , ) – решітка S
M=(A,S,s0,T,F) - автомат з алфавітом A, множиною станів S, початковим станом s0, множиною можливих станів T та функцією переходів F
M(L) – мова, яка допускається автоматом M,
Г=(N,T,S,P) – граматика з множиною не термінальних символів N, множиною термінальних символів T, початковим символом S та множиною продукцій P
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Бондаренко М.Ф., Білоус Н.В., Руткас А.Г. «Комп’ютерна дискретна математика» - Харків.: «Компанія СМІТ», 2004.
2. Джеймс А. Андерсон. Дискретная математика и комбинаторика» -Москва - Санкт-Петербург –Киев.: Издательский дом "Вильяме", - 2004, 960с.
3. Куликовский Л. Ф., Мотов В. В. «Теоретические основы информационных процессов» - М.: «Высшая школа», 1987.
4. Новиков Ф.А. Дискретная математика для программистов - Питер.: 2004.
5. Таран Т.А., Мыценко Н.А., Темникова Е.Л. Сборник задач…, -К.: -2001.
Електронні посібники
1. Акимов О.Е. Дискретная математика: логика, группы, графы. -М.: Лаборатория Базовых Знаний, 2001, -376с.
2. Алескеров Ф.Т., Э.Л.Хабина, Д.А.Шварц. БИНАРНЫЕ ОТНОШЕНИЯ, ГРАФЫ И КОЛЛЕКТИВНЫЕ РЕШЕНИЯ. – М.: Издательский дом ГУ ВШЭ 2006.
3. Аляев Ю.А., Тюрин С.Ф. Дискретная математика и математическая логика, -М.: «Финансы и статистика», 2006., 368с.
4. Горбатов В. А. Фундаментальные основы дискретной математики. Информационная математика. — М.: Наука. Физматлит, 2000. —544с.
5. Захарова Л.Е. Алгоритмы дискретной математики: Учебное пособие –М.: Гос. Ин-тэлектроники и математики, 2002, 120с.
6. Иванов Б. Н. Дискретная математика. Алгоритмы и программы: Учеб. пособие/ Б.
Н. Иванов. — М.: Лаборатория Базовых Знаний, 2003. — 288с.
7. Капитонова Ю.В. и др. «Лекции по дискретной математике» - Петербург.: СПб: БХВ- 2004, — 624 с.
8. Кузнецов О.П. Дискретная математика для инженера, -М.: 1980.
9. Кук Д., Бейз Г., Компьютерная математика, Перевод с англ. Г.М. Кобелькова, - М.: «Наука», главная редакция физико-математической литературы.
10. Москвинова Г.И. Дискретная математика. Математика для менеджера в примерах и упражнениях. Уч. Пособ, - М.: Логос, 2000, 240 с.
11. Нефедов В.Н., Осипова В.А., Курс дискретной математики. Уч. Пособие, - М.: МАИ, 1992, 264 с.
12. Нікольський Ю. В., Пасічник В. В., Щербина Ю. М. Дискретна математика. — К.: Видавнича група BHV, 2007. — 368 с.
13. Новиков Ф.А. Дискретная математика для программистов, Питер, 2004.
14. Плотников А.Д. Дискретная математика: учеб. Пособие, — М.: Новоезнание, 2005. — 288 с. 15.Соболева Т. С. Дискретная математика: учебник для студ. вузов — М.: Издательский центр «Академия», 2006. — 256 с.
16. Таран Т.А. Основи дискретної математики, - К.: Просвіта, 2003 -288 с.
17. Тишин В. В. Дискретная математика в примерах и задачах. Учебная литература для вузов. — Петербург.: СПб.: БХВ, 2008. — 352 с.
18. Шоломов Л.А. Основы теории дискретных логических и вычислительных устройств, под. редакцией С.В. Емельянова, - М.: «Наука», главная редакция физикоматематической литературы, 1980., 400с.


про публікацію авторської розробки
Додати розробку