Штучні прийоми розв’язування раціональних рівнянь
Довузівська підготовка
Тема: Штучні прийоми розв’язування раціональних рівнянь
Мета: Забезпечити первинне засвоєння учнями штучних методів розв’язування раціональних рівнянь.
Ліквідувати прогалини в знаннях учнів при розв’язуванні квадратних і лінійних рівнянь та рівнянь, що зводяться до них.
Розвивати в учнів вміння застосовувати свої знання в новій ситуації.
І. ах = в
1) а ≠ 0; х = 
(один корінь)
2) а = 0; в ≠ 0;
0 · х = в, Ø
3) а = 0; в = 0
0 · х = 0
безліч коренів,
х є R
ІІ. Д = в2 – 4ас
1) Д > 0 х1,2 = 
2) Д = 0, х = 
3) Д < 0 Ø
ІІІ. х2 + вх + с = 0
теорема Вієта економить час
ІV. 
Розв’язування рівнянь
1) х2 – 6х + 
= 
; ОДЗ х ≠ 5
х2 – 6х + 5 = 0
х = 1; х = 5 сторонній корінь
Відповідь х = 1
2) (√х – 3) (18х2 – 9х – 5) = 0
х ≥ 0
√х – 3 = 0
√х = 3
х = 9
18х2 - 9х – 5 = 0
Д = 81 + 360 = 441
= 21
х = 
= 
= 
х = 
= 
= 
стор.
2. Сума кількох невід’ємних функцій
3) 
+ 
= 0
і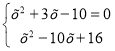 
f1(x) + f2(x) + … + fn(x) = 0
f1(x) ≥ 0 
f2(x) ≥ 0
….
fn(x) ≥ 0
4) 
+ │x2 + 6x – 16│= 0
; х = - 8 Ø
х = 2
5) 
+ │х2 – 2х│+ (х2 – 4)2 = 0
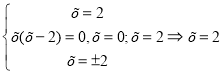
3. Скінченна ОДЗ
+ х = 1 + 
ОДЗ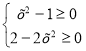 
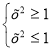
х2 = 1, х = 
Перевірка: х = 1; 0 + 1 = 1 + 0
1 = 1
х = - 1; 0 – 1 = 1 + 0
сторонній корінь – 1 ≠ 1
Відповідь: х = 1
4. Оцінка лівої і правої частин рівняння
1) 1 – х2 = 
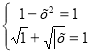x2 = 0;
f(x) = 1- x2; E (f(x) = ( - ∞; 1] x = 0
g(x) = 
перев. 1= 1
Відповідь: х = 0
2) 12 sin x + 5 cos x = 2y2 – 8y + 21
Знайти х і у
a sin x + b cos x = 
( 
)
(
) = 2y2 – 8y + 21
13 (sin x cos 
+ cos x sin ) = 2y2 – 8y + 21
13 sin (x + ) = 2y2 – 8y + 21, де = arccos 
;
f(х) = 13 sin (x + ) g(y) = 2y2 – 8y + 21
- 1
sin (x + ) 1 y0 = 
; g(y0) = 2 
- 13 13 sin (x + ) 13 E (g(y)) = [ 13 ; + 
)
і 
2y2 – 8y + 8 = 0
y2 – 4 y + 4 = 0
(y – 2)2 = 0 ; y = 2
sin (x + ) = 1
x + = 
є z
x = - + 
+ 2 
, n є z
= arccos
3) х4 + 
= 2 – (х – 1)2
а + 
2; х4 + 2 2 – (х – 1)2 2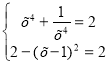 
(х – 1)2 = 0
х = 1
перевірка 2 = 2
5. Використання зростання і спадання функції
На основі теореми про корені
-
якщо в рівняння 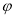(х) = а функція
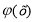зростає (спадає) на деякому проміжку
+ 2х3 = 3 – стала
х = 1, 3 = 3
2) + х3 = 3 – х х = 1 один корінь, інших немає
1 + 1 = 3 – 1
2 = 2
3) Розв. систем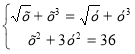 
ОДЗ 
Розглянемо функцію f(t) = 
, t 
зростаюча
Перше рівняння має вигляд f(x) = f(y) х = у на ОДЗ система
4у2 = 36
у2 = 9
у = 
3, у = 0. у = 3 отже, х = 3
Відповідь: (3; 3)
Якщо функція f(x) є зростаючою (або спадаючою) на певній множині, то на цій множині f(
) = f(
) 
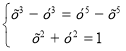
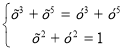f(t) = t3 + t5 – зр.
2х2 = 1; х2 = 
; х = 
(; ) (- ; - )
6. Рівняння вищих розрядів
1) х4 – 5х2 +4 = 0
2) 
= 
; х ≠ - 3
х2 – 9х = 36
х2 – 9х – 36 = 0
х = 12; х = - 3 – стор.
Відповідь: х = 12
3) х4 – 4х3 – 7х2 + 22х + 24 = 0
4) 4х 4+ 12х3 – 47 х2 + 12х + 4 = 0 : х2 зворотно симетричне х ≠ 0
4х2 + 12х – 47 + 
+ 
= 0
( 4х2 + ) + ( 12х + ) – 47 = 0
4(х2 + 
) + 12 (х + 
) – 47 = 0
Нехай х + = t;
(x + )2 = x2 + 2 · x · + = x2 + + 2 = t2
x2 + = t2 – 2
4(t2 – 2) + 12 t – 47 = 0
4t2 – 8 + 12t – 47 = 0
4t2+ 12t – 55 = 0
Д = 144 + 880 = 1024 = = 32
t = 
= 
= 
t = 
= 
= 
х + = або х + =
= =
2х2 + 2 = 5х 2х2 + 2 = - 11х
2х2 - 5х + 2 = 0 2х2 + 11х + 2 = 0
Д = 25 – 16 = 9 Д = 144 – 16 = 128
х = 
= 2 
= 
= 2· 4
= 8
х = 
= х = 
;
Відповідь: 2; ;
ax4 + вх3 + сх2 + dx + e = 0
= (
)2 – зворотно симетричне
3х3 – 7х2 – 7х +3 = 0 – симетричне
ах3 + вх2 + вх + а = 0 х = -1 завжди
(х + 1) один множник
Ділимо 3х3 – 7х2 – 7х + 3 на 3х2 – 10х + 3
3х2 – 10х + 3 = 0
Д = 100-36 = 64
х = 
= 3; х = 
= 
Відповідь: х = - 1; ; 3
ах4 + вх3 + сх2 + dx + e = 0
a + в = в + с + d = d + e обов’язково поділити на х2 – х + 1
Наприклад
х4 + 2х3 + 3х2 – 2х + 5 = 0
1+ 2 = 2 + 3 – 2 = - 2 + 5
3 = 3 = 3
многочлен х4 + 2х3 + 3х2 – 2х + 5 поділимо кутом на многочлен х2 – х + 1
одержимо х2 + 3х + 5, тому
(х2 – х + 1) (х2 + 3х + 5) = 0
х2 – х + 1 = 0 х2 + 3х + 5
Д = 1 – 4 = 0 Д = 9 – 20 < 0
Ø Ø
Відповідь: Ø
№ 347 (х – 4) (х – 5) ( х – 6) (х – 7) = 1680
№ 355 (х + 2) (х + 3) (х + 8) ( х + 12) = 4х2
(х2 – 7)2 + 6(х2 – 7) – 16 = 0
№ 351 (х2 + 2х)2 – 11 (х + 1)2 + 35 = 0
№ 350 (2х – 1)2 + (2х – 1) (х + 2) – 2 (х + 2)2 = 0 – однорідне
№ 352 (х -1)2 – 4 (х2 -1 ) + 3 (х + 1)2 = 0
№ 348 
+ 
= 
; 
- 
= 
№ 356 (х + 3)4 + (х + 5)4 = 16
про публікацію авторської розробки
Додати розробку