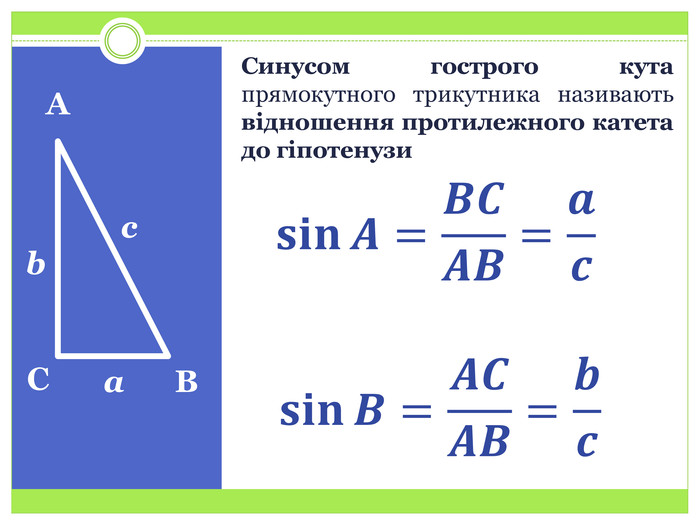
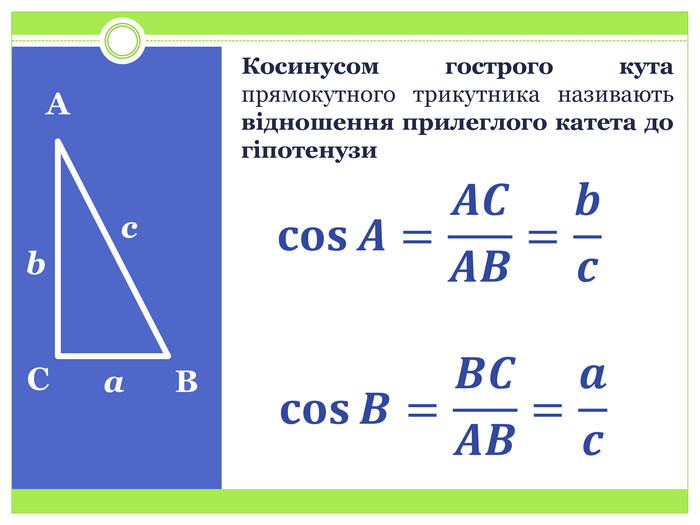
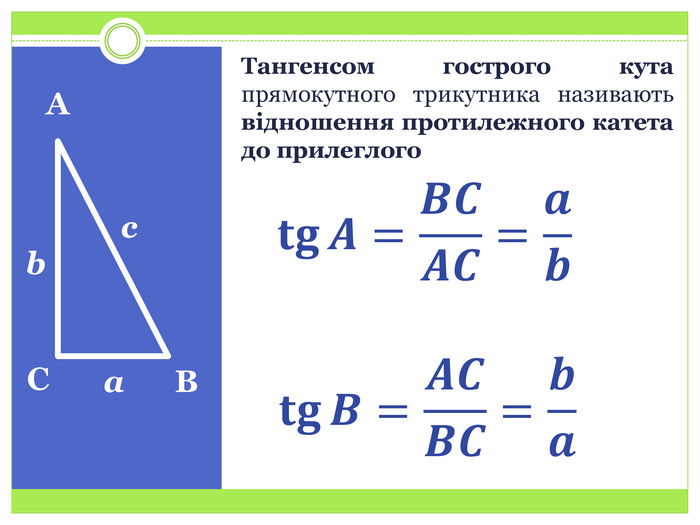
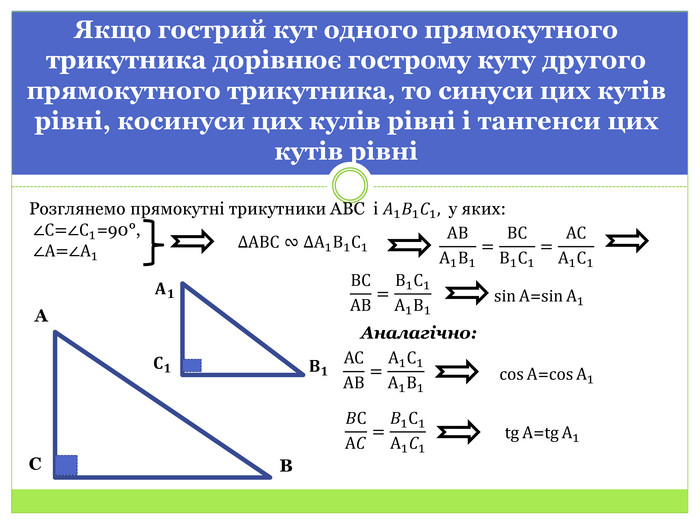
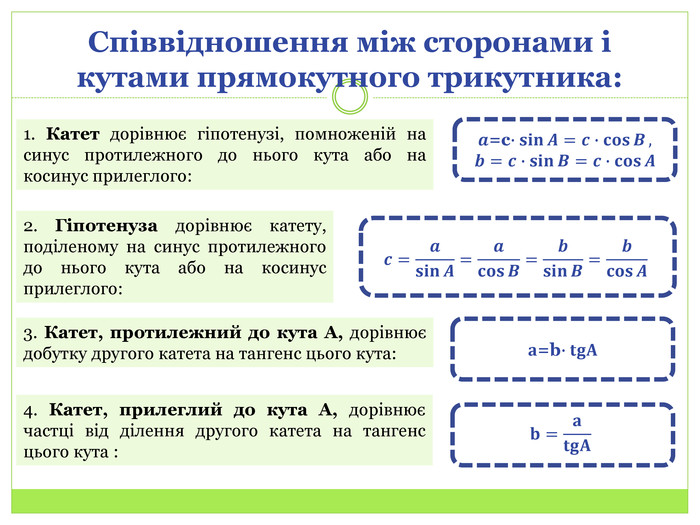
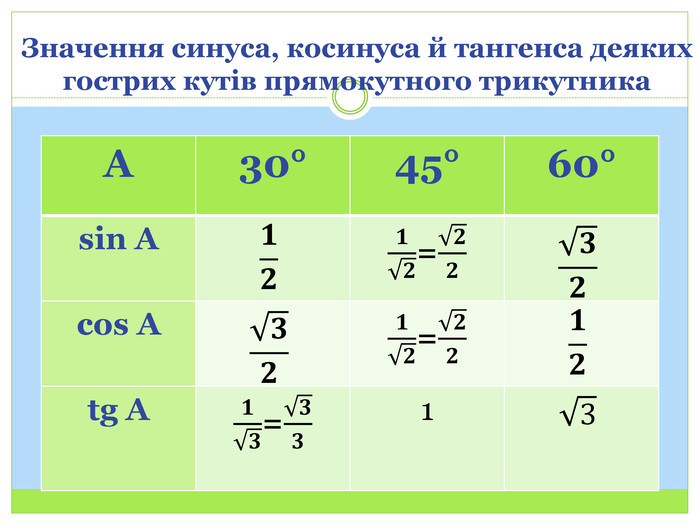
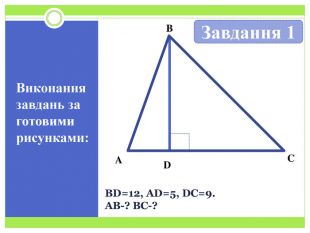
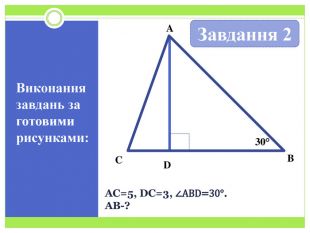
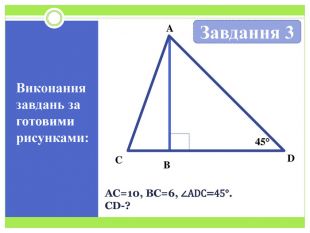
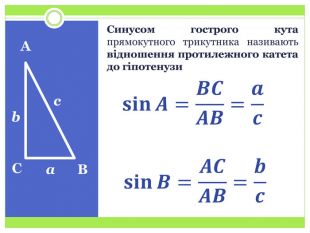
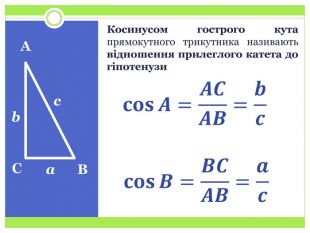
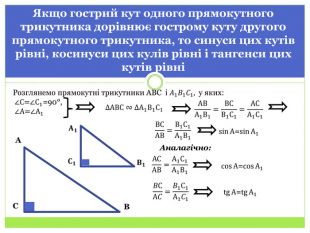
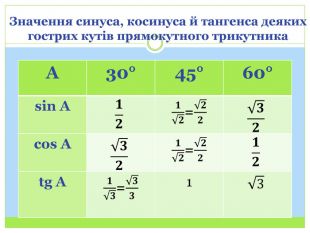
Синус, косинус і тангенс гострого кута прямокутного трикутника
Про матеріал
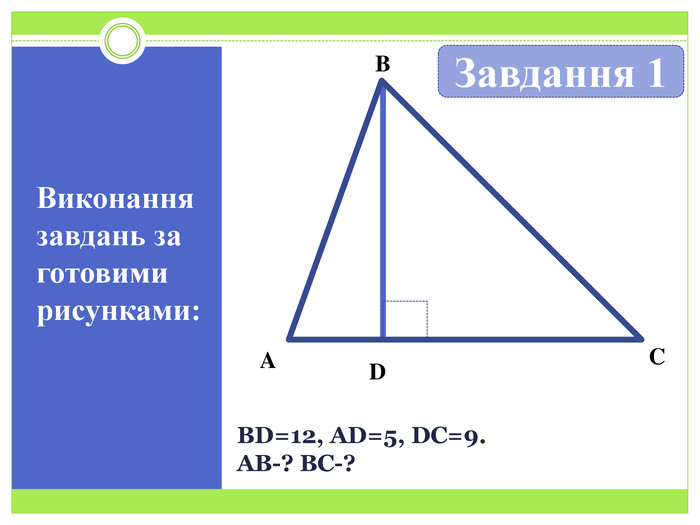
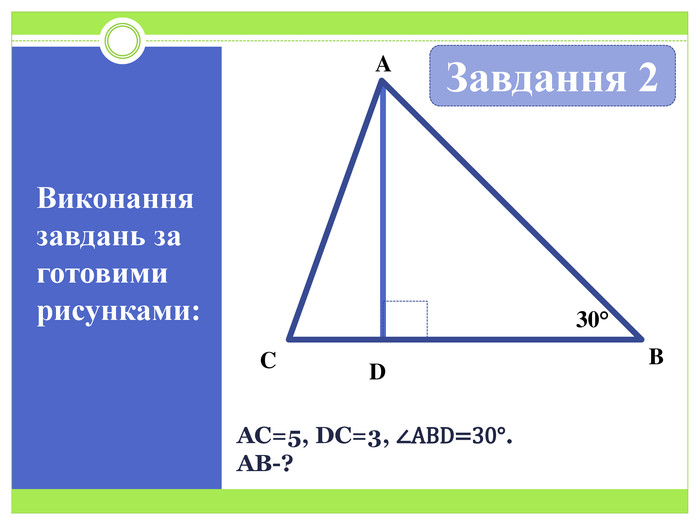
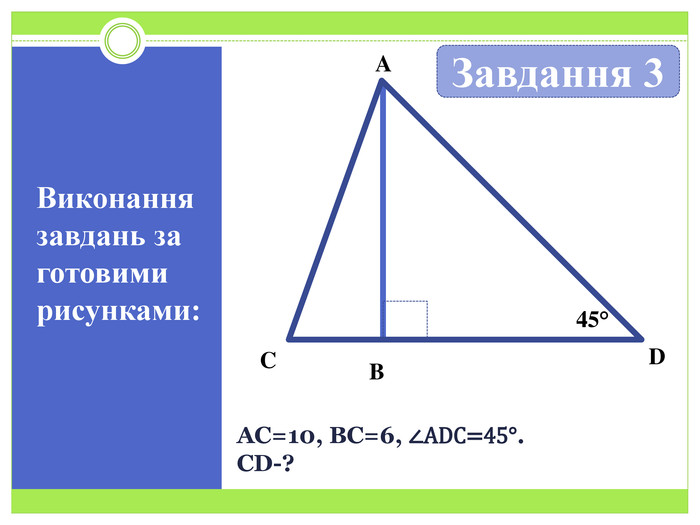
Презентація до уроку геометрії 8 класу на тему "Синус, косинус і тангенс гострого кута прямокутного трикутника" Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Саме те,що потрібно всім учням по геометрії))
-
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку