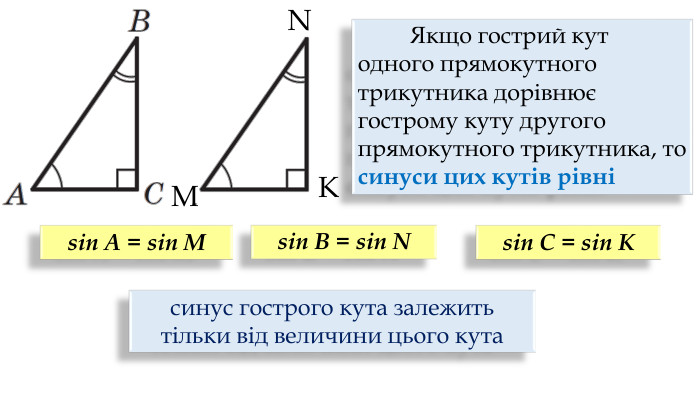
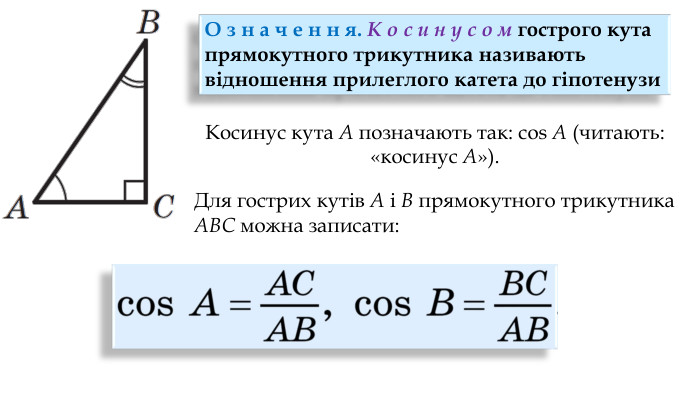
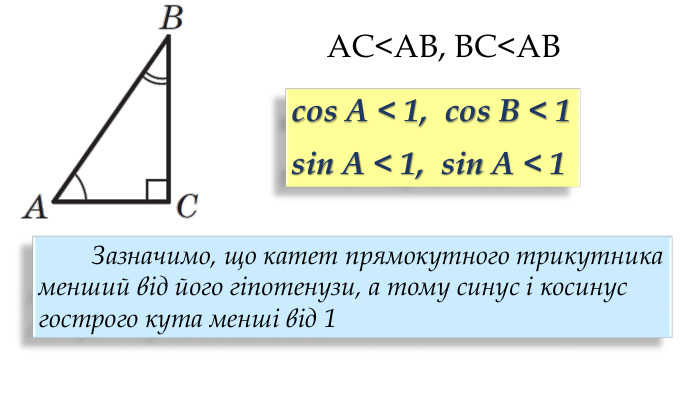
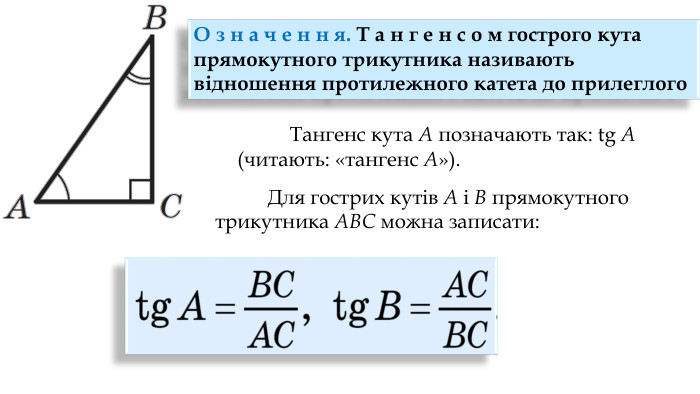
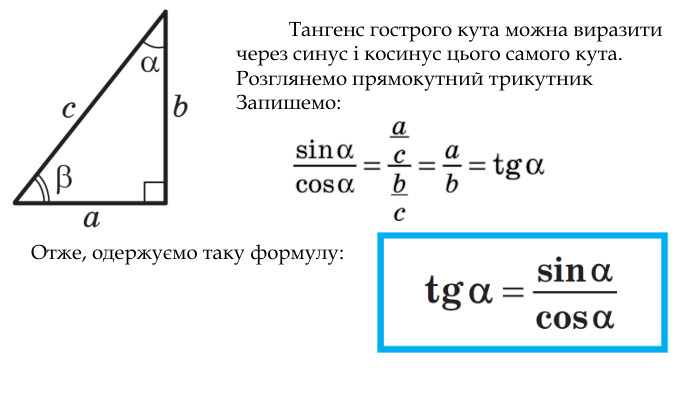
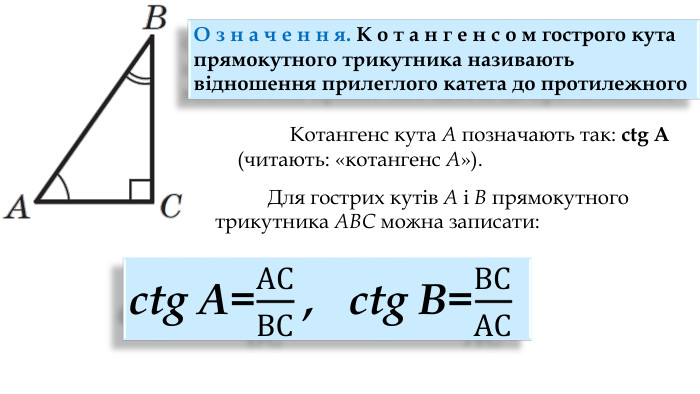
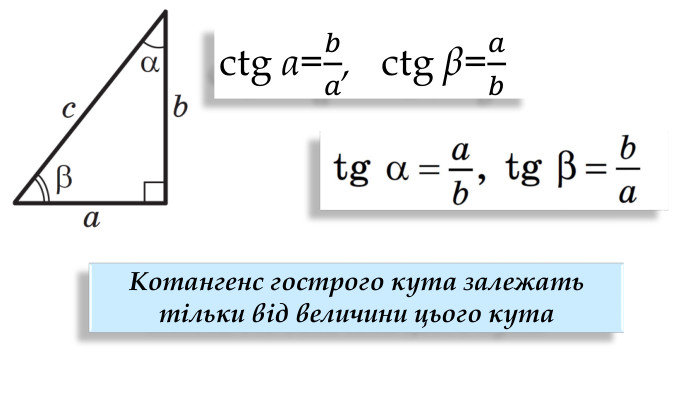
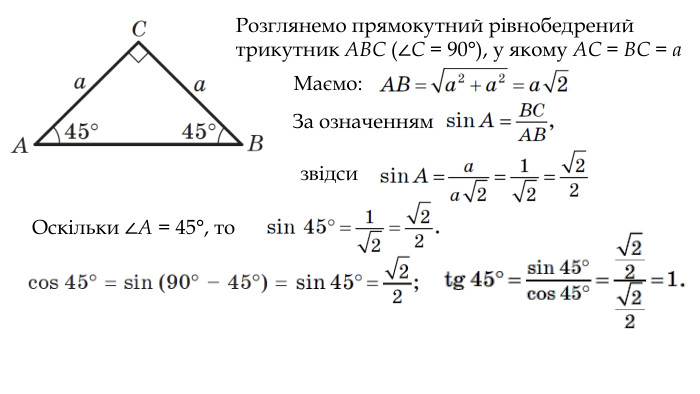
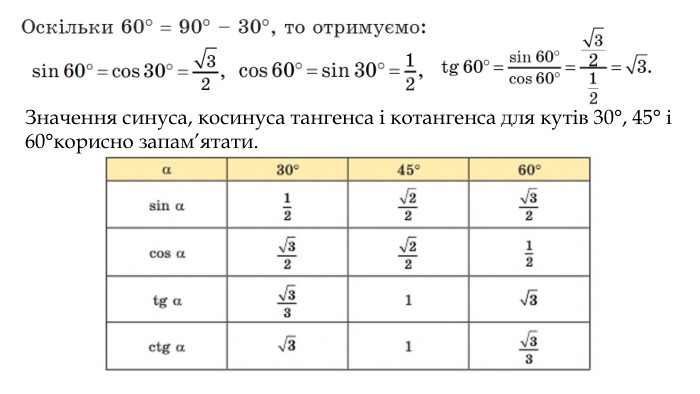
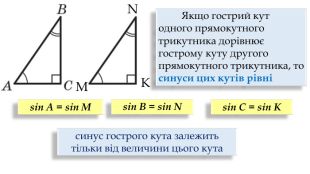
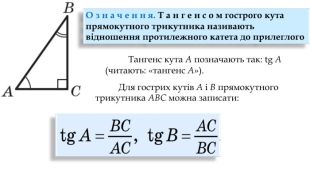
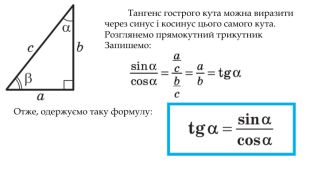
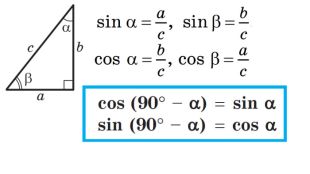
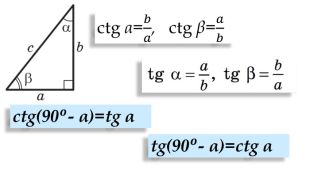
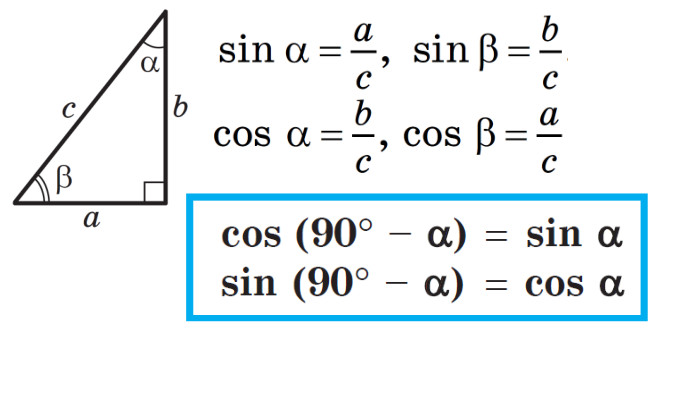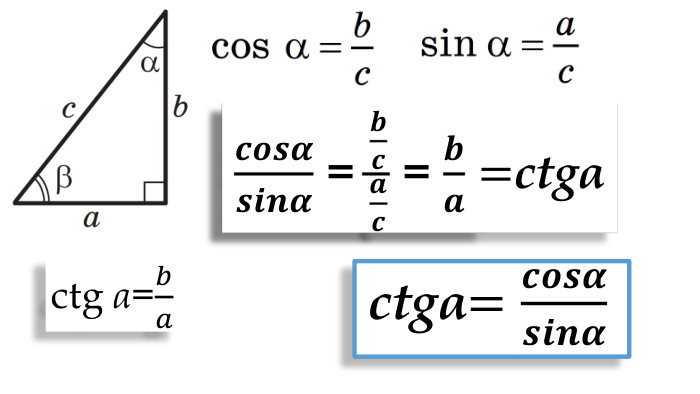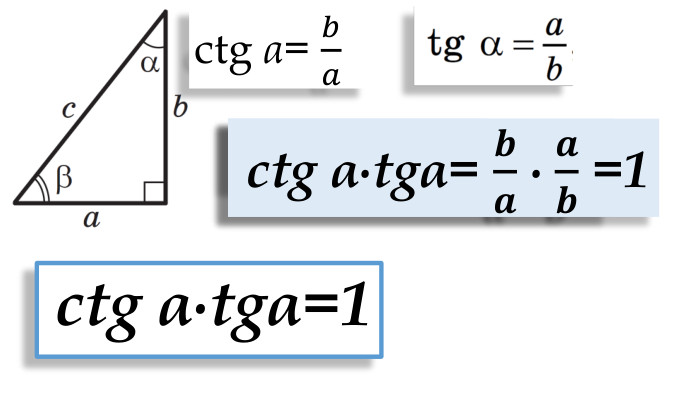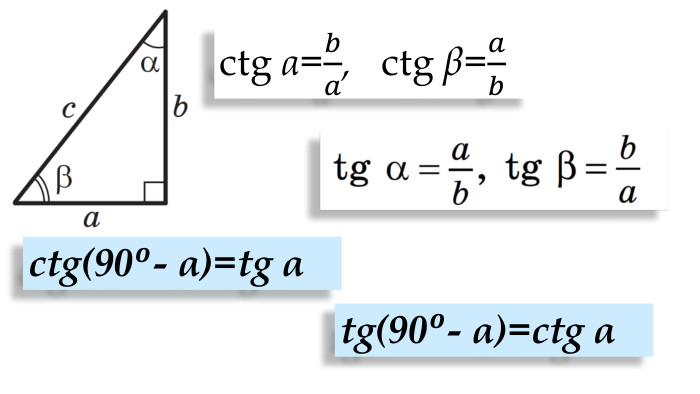Синус, косинус, тангенс гострого кута прямокутного трикутника
Про матеріал
До вашої уваги презентація, яка дозволить сформувати нові знання про тригонометричні співвідношення для прямокутного трикутника. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку