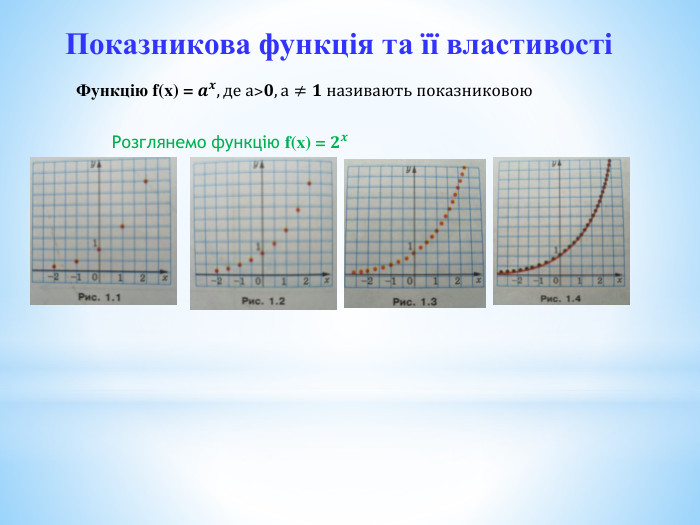
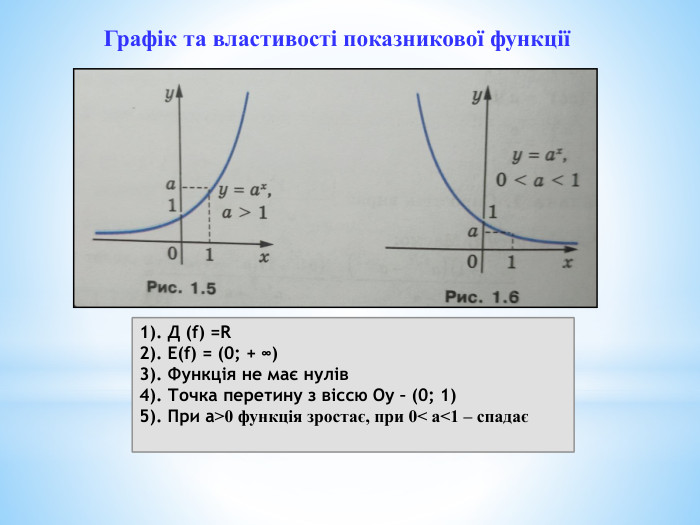
Презентація до уроку "Степінь з довільним дійсним показником. Показникова функція"
Про матеріал
Матеріал дає можливість повторити степінь з натуральним та цілим від'ємним показником, пригадати властивості степенів, а також ввести поняття степеня з дійсним показником
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку