Стародавні доведення
Про матеріал
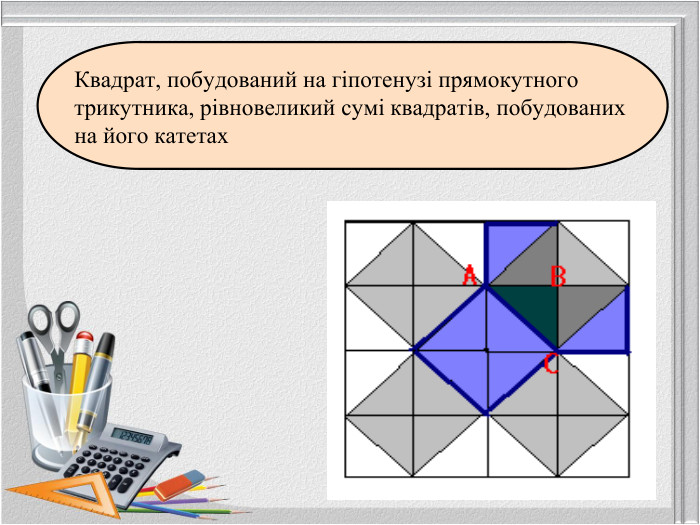
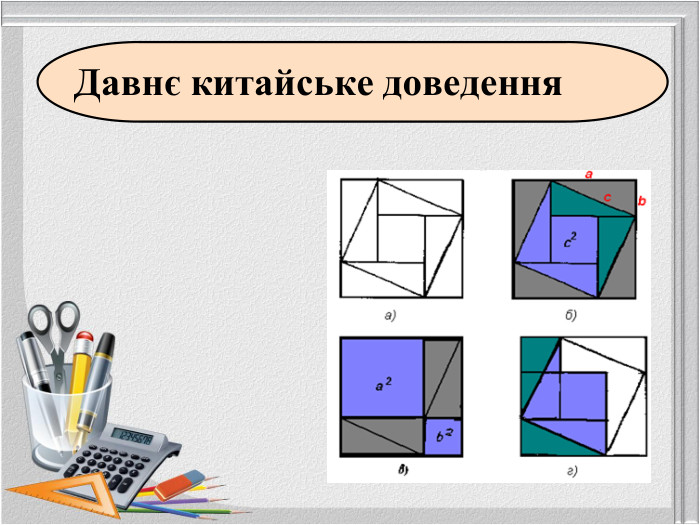
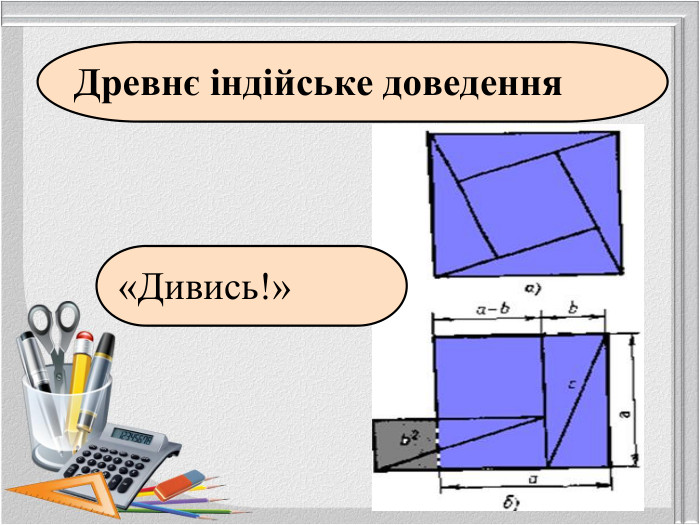
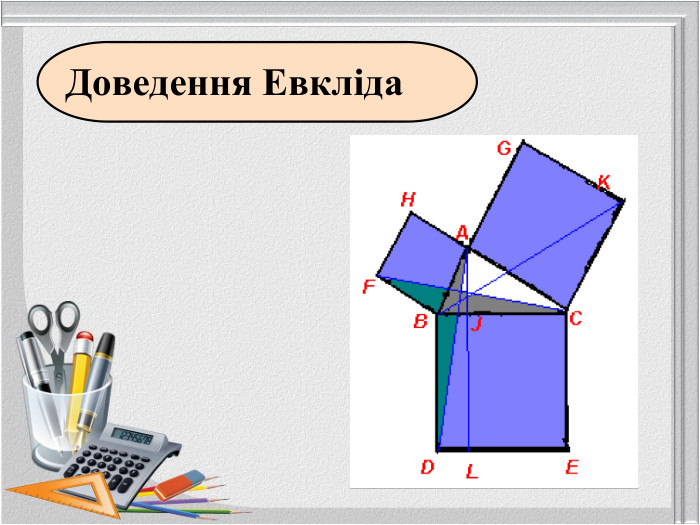
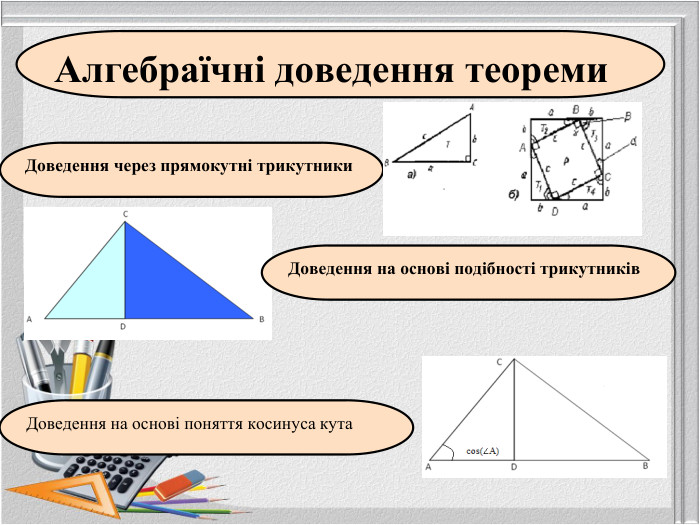
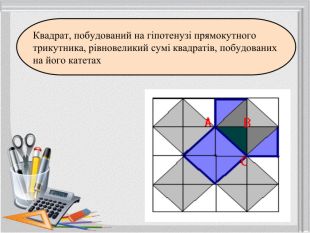
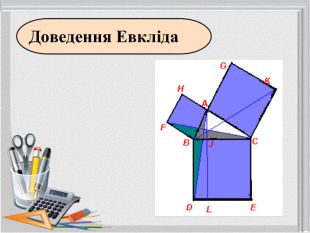
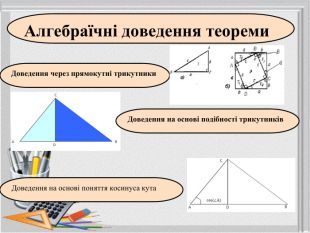
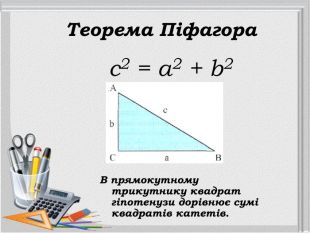
Так теоремою Піфагора займалося багато математиків протягом багатьох століть. Частинні випадки теореми були відомі в Єгипті, Вавилоні, Китаї. На сьогодні відомі різні підходи до доведення відомої теореми, але сутність її не змінюється.
Перегляд файлу
Зміст слайдів

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку