Стаття "Формування логічної компетентності учнів на уроках математики"

ФОРМУВАННЯ ЛОГІЧНОЇ КОМПЕТЕНТНОСТІ УЧНІВ НА УРОКАХ МАТЕМАТИКИ

    Спеціалізована загальноосвітня школа № 27 імені Дмитра Іваха, вчитель математики вищої категорії Волєва Інна Миколаївна

Пам’ятайте: якщо ви хочете

навчитися плавати, то сміливо

заходьте у воду, а якщо хочете

навчитися розв’язувати задачі,

то розв’язуйте їх!  

Д. Пойа

     Основним засобом навчання математики є задачі. Для формування умінь розв’язувати математичні задачі необхідно навчити учнів спеціальним знанням про задачі та їх розв’язування. Для цього вчитель, як правило, основну увагу приділяє пошуку розв’язання та його запису. Важливо збагатити учнів загальними методами розв’язування задач, бо не кількість розв’язаних задач, а метод їх розв’язування визначає навчальний ефект.    

     Найскладнішим завданням вчителя є формування в учнів логічної компетентності – вміння володіти та застосовувати математичні методи доведення і спростування тверджень. Довільне твердження має бути чітко обґрунтованим, тобто має супроводжуватися достатньо сильними аргументами, які б підтверджували його істинність [1]. До того ж доведення об’єднують геометричні істини в систему наукових знань.

    У широкому розумінні слово «доведення» - це процедура встановлення істинності твердження як за допомогою логічних міркувань, так і безпосередньо через чуттєве сприйняття деяких фізичних предметів та явищ [2]. Вперше в геометрію ввів ідею доведення родоначальник грецької математики вчений-геометр Фалес. Починаючи з часів Евкліда незмінною залишається структура математичного доведення як демонстрація «неочевидної» істини шляхом переходу до неї від «очевидних» істин або встановлених раніше за допомогою послідовності явних «очевидно законних» умовиводів [3,4].

    Рене Декарт у своїй роботі «Міркування про метод» писав «Метод – це спосіб правильно спрямувати свій розум і відшукати істину». На уроках математики учні знайомляться з різними методами доведення: від супротивного,  математичної індукції, геометричних перетворень, векторним, координатним, алгебраїчним. Але найбільш важливими являються  синтетичний метод, аналітичний метод та аналітико-синтетичний метод.

    Синтез – це метод міркувань від даних до шуканих, невідомих величин.     Синтетичний метод доведення пов’язаний з аналізом Евкліда. При використанні синтетичного методу доведення починають з умови і поступово приходять до висновку. Практика показує, що учні краще сприймають синтетичний метод доведення, оскільки виводити необхідні ознаки простіше, ніж підбирати достатні умови для виконання висновків тверджень.

    Синтетичний метод успішно використовується тоді, коли «ланцюг висновків легко відкривається», коли саме формулювання задачі прямо підказує, які висновки випливають з даних умов.

    Алгоритм пошуку доведення теореми або розв’язання задачі на доведення синтетичним методом:

1. Припустимо, що висновок теореми або задачі на доведення правильний;
2. Вивести з цього твердження всі можливі наслідки;
3. Переконатися, що ці наслідки є очевидними або раніше доведеними твердженнями;
4. Вибравши одержаний правильний висновок за вихідне твердження, провести міркування в оберненому порядку і прийти до висновку про правильність умови теореми або задачі.

    Синтетичний метод доцільно використовувати в курсі геометрії при доведенні перших теорем а також тоді, коли задача легка або вже відомий спосіб її розв’язування. Такі доведення чіткі, короткі, однак вони не позбавлені деяких недоліків: дітям не зрозуміло чому міркують так, а не інакше; додаткові побудови не аргументуються. Компенсувати недоліки синтетичного методу доведення теорем потрібно такими методичними прийомами:

⸺ формулювання ідеї доведення;

 ⸺ мотивація додаткових побудов;

⸺ формулювання плану доведення;

⸺ проведення доведення з опорою на короткий запис;

⸺ складання опорної схеми доведення;

⸺ складання таблиці з двома колонками: твердження і обґрунтування.

   Як приклад доведемо теорему про властивість медіани рівнобедреного трикутника.

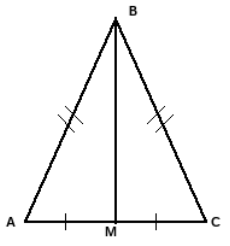Дано: Δ АВС – рівнобедрений,  ВМ – медіана.

 Довести: 1) ВМ– бісектриса;

                 2) ВМ – висота.

                Доведення:

    Аналіз – це метод міркувань від невідомих, шуканих до даних величин.

    Аналітичний метод передає послідовність міркувань, розпочинається з постановки проблеми, а не аксіом чи раніше доведених теорем як у синтетичному методі. При аналітичному методі пошук доведення здійснюється від висновку до умови. Доведення цим методом спрямовується двома запитаннями: «Що треба довести?» і «Що для цього потрібно знати?» При цьому хід міркувань стає більш вмотивованим, природнім, легше виділяти ідею та план доведення.

   Алгоритм аналітичного методу доведення:

1. Вияснити з якого раніше відомого твердження (або аксіоми) випливає висновок твердження, що доводиться.
2. Якщо такого твердження не вдається знайти, то потрібно шукати інше, можливо поки що не доведене, з якого слідував би висновок твердження, що доводиться.
3. Далі шукати інше твердження, з якого би слідувало попереднє, і так далі, поки не дійдемо до твердження, яке слідує з умови теореми або задачі.
4. Оскільки весь ланцюжок достатніх умов задовольняється для виконання висновку, то дане твердження доведене.

    Наприклад, зразок пошуку доведення аналітичним методом.

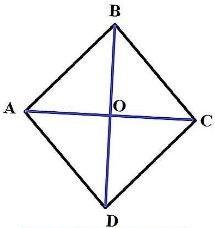
    Теорема. Діагоналі ромба є бісектрисами його кутів.

              Питання:

⸺ Що потрібно спочатку довести, щоб довести, що ВД – бісектриса ∠ АВС?     (Відповідь: що ∠ АВД = ∠ СВД)

⸺ Як довести рівність цих кутів?

(Відповідь: треба довести рівність трикутників АВД і СВД)

⸺ Чи рівні ці трикутники? (Відповідь: так, за ІІІ ознакою рівності трикутників) і т. д.

    Після доведення теореми корисно давати учням завдання такого виду: «Спробуйте сказати одним реченням, у чому суть доведення теореми?», «Сформулюйте ідею доведення», «Що потрібно запам’ятати?». Вчитель має давати зразки таких розгорнутих формулювань.

Засвоєнню теореми після її доведення сприяють також завдання видів:

   ⸺ Сформулюйте теорему в формі твердження «Якщо… , то…»;

   ⸺ Сформулюйте обернене твердження;

   ⸺ Відтворіть доведення теореми за готовим рисунком (при цьому змінити положення та позначення елементів);

   ⸺ Сформулюйте твердження, які використовують при доведенні;

   ⸺ Доведіть теорему іншим методом ( координатним, векторним чи методом геометричних перетворень);

   ⸺ Розв’яжіть задачу на застосування теореми.

    У систему вправ на застосування теореми, як і на застосування понять, доцільно включати вправи, що провокують на помилки, контр приклади

    Аналітичний метод величезну роль відіграє в пошуку доведення теореми або задачі, а синтетичний це безпосередня реалізація даного проекту.

    Формування в учнів навичок аналізу і синтезу сприяє свідомому засвоєнню ними теоретичного матеріалу, активному розв’язанню задач різних типів.   

    Аналітико-синтетичний метод доведення полягає в тому, що пошук доведення починають аналітичним методом (доведення починають від вимоги), але міркування не доводять до кінця, а, спиняючись на певному кроці, починають міркування у зворотному напрямі, тобто з розгортання умови синтетичним методом, і ним же закінчують доведення. Наведемо приклад розв’язування задач на доведення цим методом.                                                                         

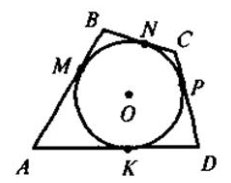Довести, що у чотирикутника, описаного навколо кола, суми довжин протилежних сторін рівні. 

                           Доведення.                                                                       

    Щоб довести, що AB + CD = BC+ AD,

    досить довести, що

 AM + BM + CР + DР = DК + AК + BN + CN, де M, N, K, Р – точки дотиків кола і чотирикутника. За властивістю дотичних, проведених з однієї точки до кола, AM = AК, BM = BN, CР = CN, DР = DК. Додавши ці рівності почленно дістанемо AM + BM + CР + DР = ДК + АК + CN + BN, що і потрібно було довести.

    У цьому доведенні міркування здійснювались послідовно: то від висновку теореми, то від умови. Рух із протилежних боків у загально випадку виконують доти, доки міркування не дійдуть спільного твердження, або суперечливих висновків. Зазначимо, що аналітико-синтетичний метод особливо зручний тоді, коли перетворення лише умови чи лише висновку теореми (задачі) не приводить до потрібної мети. 

    Навчити доводити означає навчити міркувати. Завдання «Довести твердження: …» належить до одного з найважливіших типів нестандартних задач, а питання про пошук доведення – частковий випадок загального питання про пошук розв’язування задачі.

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ

1. Слєпкань З.І. Методика навчання математики: Підручник.–2-ге вид., допов. і переробл.–К.: Вища шк.., 2006.–582с.

2. Лоповок Л.М. Варианты доказательства геометрических теорем//Математика в школе.–1975.-№5.-С.29-31.

3. Гришина Т. Рівнева організація роботи над теоремою//Математика в школі.– 2002.-№1.-С.17-20.

4. Єршов Ю. Доказовість у математиці//Математика в школі.–2006.-№10.-С.2-8.

5. Резніченко Р. Формування прийому вивчення теорем за текстом підручника// Математика в школі.–2003.-№6.-С.33-35.