Стаття на тему: "Структура та зміст факультативного заняття з теми «Геометрична ймовірність» (9 клас)"

Автори:

Окопний Руслан, магістрант, спеціальності «Середня освіта (Математика)».

Розуменко Анжела Оурелянівна, кандидат педагогічних наук, доцент кафедри математики Сумського державного педагогічного університету імені А.С.Макаренка.

 

Структура та зміст факультативного заняття з теми «Геометрична ймовірність» (9 клас)

 

Елементи стохастики є однією із змістовних ліній шкільного курсу математики. Відповідний навчальний матеріал має потужний потенціал щодо формування світогляду учнів та реалізації прикладної спрямованості шкільного курсу математики. Вважаємо за доцільне деякі поняття даної змістової лінії більш глибоко розглянути на факультативних заняттях. Пропонуємо розробку факультативного заняття з теми «Геометрична ймовірність», що містить деякі теоретичні питання, приклади класичних ймовірнісних задач та задачі прикладного змісту для самостійного розв’язування учнями. Факультативне заняття з теми «Геометрична ймовірність» може мати таку структуру:

1. Історичний огляд розвитку ймовірнісних ідей.
2. Основні поняття теорії ймовірностей.
3. Задача про зустріч .
4. Прикладні задачі дослідницького характеру.

Розглянемо орієнтовний зміст кожного етапу. 

1. Історичний огляд розвитку ймовірнісних ідей

У розвитку будь-якої науки дослідники виділяють чотири основні етапи, а саме:

1. Етап зародження наукової теорії.
2. Етап первинного обґрунтування.
3. Етап достатнього обґрунтування.
4. Етап остаточного обґрунтування.

Розглянемо формування деяких ймовірнісних ідей у їх історичному розвитку.

З давніх-давен були відомі події, щодо яких не можна із впевненістю заявити, відбудеться воно чи ні при черговому спостереженні. Хто народиться в сім'ї - хлопчик чи дівчинка? Чи доживе особа А, якій виповнилося 35 років, до 70? Подібних питань виникало досить багато, але вони обговорювалися лише в філософському сенсі.

Зараз важко встановити, хто вперше поставив питання про вимірювання самої можливості появи випадкової події. У літературних творах, таких, як «Божественна комедія» Данте, неодноразово зустрічаються зауваження про гру в кості (в сучасному розумінні «гральні кубики») і навіть спроби підрахувати кількість сприятливих можливостей тієї чи іншої комбінації. Більш чіткі постановки питань вперше зустрічаються в одному з перших математичних творів початку італійського Відродження, написаному Лукою Пачолі (1445-1514), яке носило назву «Сума знань з арифметики, геометрії, відносинам і пропорційності». Задачі Пачолі і подібні до них зіграли важливу роль у формуванні теорії ймовірностей. Вони були розміщені в розділі незвичайних задач.

Схожими задачами цікавився  італійський лікар, математик і філософ, Джероламо Кардано (1501-1576). В рукописі «Книга про гру в кості», який датовано самим Кардано 1526 роком, але виданий лише в 1663 році, було розв’язано  багато задач, пов'язаних із киданням гральних кісток і випаданням на них того чи іншого числа очок. Вчений правильно підрахував кількість різних випадків, які можуть відбутися під час кидання двох або трьох кісток. Його цікавили також історія азартних ігор і різні прийоми шахрайства, які використовуються гравцями.

До задач про розподіл ставки також звертався Н. Тарталья (1494-1559). Йому належить  книга «Загальний трактат про міру і число», яка була опублікована в 1556 році. Треба зауважити, що Тарталья в зазначеному трактаті правильно розв’язав деякі питання комбінаторики.

Заслуговує на увагу внесок у цей розвиток відомого астронома і фізика Галілео Галілея (1564-1642). Його робота «Про вихід очок при грі в кості», яка побачила світ лише в 1718 році, була присвячена підрахунку числа можливих результатів при киданні трьох кісток. Галілей запропонував при підрахунках занумерувати кості. Можливі результати записувалися у вигляді трійок чисел, причому на відповідному місці стояло число очок, яке випало на кістці з даним номером. Ідея настільки ж проста, наскільки і геніальна.

Вважають, що теорія ймовірностей зародилася в листуванні двох великих геніїв - Б. Паскаля (1623-1662) і П. Ферма (1601-1665). Збереглися лише три листи Паскаля і чотири листи Ферма. В цьому листуванні поняття ймовірності ще відсутнє і обидва автори використовують лише порівняння чисел, що сприяють випадковим подіям випадків. Але зате саме у них вперше були правильно розв’язано задачу про розподіл ставки. У запропонованому розв’язанні вчені розглядають рівноможливі наслідки, що пізніше лягли в основу класичного означення ймовірності. Це був серйозний крок у створенні передумов зародження теорії ймовірностей як науки. Подальший розвиток ймовірнісні ідеї отримали в дослідженнях Х.Гюйгенса, П.Лапласа, Я.Бернуллі, К.Гаусса та інших відомих математиків. Автором сучасної аксіоматики став радянський вчений А.М.Колмогоров.

2. Основні поняття теорії ймовірностей

Розглянемо два поняття теорії ймовірностей – «випробування» і «подія». Поняття «випробування» найпростіше описати, розглянув­ши викидання грального кубика, на гранях якого проставлені числа 1, 2, 3, 4, 5, 6. Кожне викидання при однакових умовах будемо нази­вати випробуванням. Іншими прикладами випробування є підкидання монети, витягування карти з добре перемішаної колоди тощо.  У за­гальному випадку під випробуванням будемо розуміти здійснення пев­ного комплексу умов, які можна відновити довільне число разів. Наслідки випробування будемо називати подіями (випадання чи­сла «5» на кубику, «решки» при підкиданні монети, витягування «туза бубнового» з колоди карт тощо).

Якщо в результаті випробування деяка подія може відбутись, а може не відбутись, то вона називається випадковою. Випадкові події позначаються літерами A, B, C, D, … .

Випадкові події, які не можна розкласти на простіші, називаються елементарними. Можлива елементарна подія — це кожний із можливих результатів окремого випробування.

Усі події можна поділити на вірогідні, неможливі та випадкові.

Вірогідною (достовірною) будемо називати подію, яка обов’язково

настане в результаті випробування .

Неможливою називається подія, яка в результаті випробування ніколи не відбудеться  .

Випадковою називається подія, яка в результаті випробування  може відбутися, а може і  не відбудеться.

 Класичне означення ймовірності

Розглянемо деяке випробування і подію, пов’язану з ним. Кожен з його можливих наслідків назвемо елементарною подією ( елементарним наслідком).

Елементарні наслідки, при яких подія, що нас цікавить відбувається, називаються сприятливими цій події.

Означення. Імовірністю випадкової події А називається відношення кількості елементарних подій, які сприяють появі цієї події, до загальної кількості  рівноможливих елементарних подій , де - число елементарних подій, сприятливих до появи події  А, - число всіх можливих елементарних подій (наслідків) експерименту.

Властивості ймовірності

1. Ймовірність достовірної  події дорівнює одиниці

2. Ймовірність неможливої події дорівнює нулю

3. Ймовірність випадкової події є невід’ємне число, що знаходиться між нулем і одиницею: 0 < Р(А) <1.

Приклад. В урні сто занумерованих жетонів з номерами від 1 до 100. Яка ймовірність того, що номер навмання вийнятого з урни жетона не містить цифри 3?

Розв’язання. Нехай подія  – номер навмання вийнятого з урни жетона не містить цифри 3.

За класичним означенням ймовірності .

 Безпосереднім підрахунком знаходимо, що кількість чисел у межах першої сотні, які містять цифру 3, дорівнює 19. Це числа 3, 13, 23, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 43, 53, 63, 73, 83, 93. Тоді чисел, що не містять цифри 3, буде . Таким чином, , тоді .

Класичне означення ймовірності можна використовувати лише для експериментів з обмеженим числом рівноможливих елементарних подій.

 Статистичне означення ймовірності

Для більшості задач, особливо економічних, обчислити ймовірності практично неможливо. У цьому разі використовується статистична ймовірність. Насамперед уводиться поняття відносної частоти випадкової події W (A).

Нехай деяке випробування повторюється разів, – число випробувань, в яких подія відбулася.

Означення. Відносною частотою появи події називається відношення числа випробувань, в яких подія відбулася до загального числа всіх проведених випробувань:

.

Довготривалі спостереження над появою або не появою події A при великій кількості повторних випробувань за одних і тих же умов показують, що для широкого кола явищ число появ або не появ події A підлягає стійким закономірностям, а саме: якщо позначити через m число появ події A при n незалежних випробуваннях, то виявляється, що відношення для достатньо великих n зберігає майже сталу величину.

Існує великий експериментальний матеріал з перевірки факту стійкості частот багатьох явищ. Наприклад, результати підкидання монети, представлені в наступній таблиці (таблиця 1).

 

Таблиця1

Експериментатор, що підкидав монету	Число кидань	Число випадання герба	Частота W (A) випадання герба
Бюффон	4000	2018	0,5080
К. Пірсон	12000	6019	0,5016
К. пірсон	24000	12012	0,5005

 

Теорія ймовірностей вивчає лише такі випадкові події, в яких спостерігається стабільність відносних частот.

Статистичну ймовірність можна використовувати тільки для задач із скінченною множиною проведених експериментів. Але в реальному житті є велика кількість задач, де множина всіх можливих результатів випробування є нескінченною. В таких випадках використовують геометричну ймовірність.

 

 Геометрична ймовірність

Геометричну ймовірність вводять для трьох видів простору: одновимірного (на прямій); двовимірного (на площині); тривимірного ( у просторі). В залежності від виду простору формулюють подію і обчислюють ймовірність (таблиця  2).

Таблиця 2

Геометричний простір	Випадкова подія	Ймовірність випадкової події
Одновимірний (пряма)	Точка, кинута на великий відрізок попаде на малий	Відношення довжин відрізків - менший відрізок - більший відрізок
Двовимірний (площина)	Точка, кинута на велику фігуру  попаде на малу	Відношення площ фігур - площа меншої фігури - площа більшої фігури
Тривимірний (простір)	Точка, кинута у велике тіло попаде у мале	Відношення об’ємів тіл - об’єм малого тіла - об’єм великого тіла

Наведемо приклади задач для одновимірного та двовимірного геометричних просторів.

Приклад 1. Абонент чекає на дзвінок протягом однієї години. Яка ймовірність того, що йому зателефонують протягом перших п’ятнадцяти хвилин?

Розв'язання: якщо відрізок часу, що відповідає годині прийняти за одиничний, то п'ятнадцять хвилин буде дорівнювати його четвертій частині. Отже, відношення довжин відповідних відрізків (одновимірний геометричний простір), а значить і шукана ймовірність  дорівнює .

Приклад 2. В круг вписано квадрат. У круг навмання кидають точку. 
Знайти ймовірність того, що вона виявиться всередині квадрата.
           Розв'язання: Для кращого уявлення виконаємо малюнок до задачі (Рис.1)                    
Нехай сторона квадрата (A) дорівнює , тоді його площа .

Діаметр круга (Ω) рівний   , тоді площа цього круга  

Оскільки квадрат знаходиться всередині круга , то ймовірність умови обчислюється як відношення площ за формулою: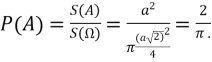  

Відповідь: .

3. Задача про  зустріч.

Два учні призначили зустріч у  певному місці між третьою та  четвертою годинами дня. Той, хто прийде перший, чекає іншого впродовж 15 хв, після чого йде з місця зустрічі. Знайти ймовірність того, що зустріч відбудеться.

Розв’язання. Позначимо через x  час (у  годинах) приходу на місце зустрічі першого учня, а через y — другого. Очевидно, що  година, під час якої має відбутися зустріч, несуттєва, тобто учні мають зустрітися протягом однієї години. Тоді для x і y виконуються умови 0 ≤ x ≤ 1 і 0 ≤ y ≤ 1,

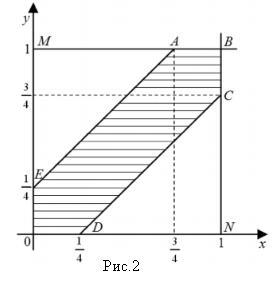
і геометричним зображенням простору Ω є одиничний квадрат OMBN (Рис.2).

Нехай подія A полягає в тому, що зустріч відбулася. Це можливо лише тоді, коли різниця між часом приходу на місце зустрічі першого та другого учнів не більша за 15 хв, або   год, тобто

. (*)

Звідси отримуємо систему нерівностей  ,    .

Множина точок, координати яких задовольняють нерівності (*), утворює фігуру ABCDOE (Рис. 9):

AE – пряма ,  DC – пряма   .

Оскільки ,

Причому ,     ,

то  .

Отже, ймовірність того, що зустріч відбудеться, .

Розглянемо цю задачу в більш загальному вигляді.

Двоє осіб домовились зустрітися в певному місці у проміжку часу від годин, а також про те, що той, хто прийде першим, чекатиме на другого протягом τ годин. Знайти ймовірність того, що зустріч відбудеться, якщо кожна особа може прийти в довільний момент часу t є

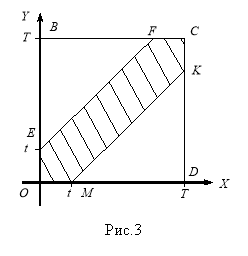
Розв’язання. Подія А — «зустріч відбудеться». Позначимо довжину часового проміжку а моменти приходу кожної особи — Тоді подія А відбудеться за умови де Зобразимо ці умови на площині в системі координат (Рис. 3). Як бачимо з рис. 10, часу Т відповідає площа квадрата а події А — площа шестикутника Скориставшись геометричним означенням імовірності, дістанемо:

Зокрема, коли ,  отримаємо

 .

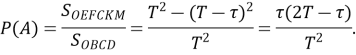
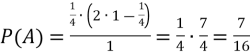Цікаво відзначити, що коли , отримаємо

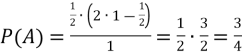,  хоча часто «інтуїтивно» в цьому випадку передбачається ймовірність .

Задача про зустріч може мати різні формулювання.

Наприклад: два судна повинні підійти до одного причалу. Поява суден є незалежними подіями, рівноможливими протягом доби. 
Знайти ймовірність того, що одному з суден доведеться чекати звільнення причалу, якщо час стоянки першого судна – 1 год, а другого – 2 год. 
            Розв'язання: Нехай перше судно прийшло до причалу в u год і стоїть 1 годину, а друге судно прийшло до того ж причалу в v год і стоїть 2 години.
Тоді простором елементарних подій, що є всіма можливими результатами випробування є  множина впорядкованих пар чисел

Ω = .

Події А, яка полягає в тому, що «судна зустрінуться», тобто суднам прийдеться чекати звільнення причалу, відповідає множина точок

А = , що утворюють заштриховану область на рисунку (Рис.4). Обчислюємо ймовірність події як відношення площ

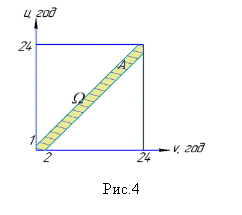Відповідь:

Можна знайти й інші формулювання цієї класичної задачі, яка відома під назвою «задача про зустріч».

 

 

 

4. Прикладні задачі дослідницького характеру

Під прикладною задачею стохастики розуміють задачу, що виникла в реальній життєвій ситуації або інших наукових галузях для розв’язання якої необхідно використати ймовірнісні поняття та методи.

Задача 1 ( з телевізійної гри «Що? Де? Коли?»)

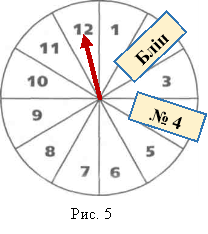Правила гри дуже прості та відомі всім. Уявіть, що одного разу під час гри склалася така ситуація: після 10 раундів рахунок виявився рівним 5:5. Отже, останній раунд мав бути вирішальним. При цьому конверти із завданнями розміщувалися таким чином як показано на рисунку (Рис.5). Гравці звернулися до ведучого з проханням поміняти розміщення конвертів, тому що ймовірність випадання «Бліцу» є найбільшою порівняно з іншим конвертом, що залишився. Чи дійсно вимога була обґрунтованою? Поясніть вимогу гравців.

Розв’язання. З рисунку видно, що ймоврність випадання кожного сектору на початку гри є однаковою і дорівнює Але після 10 раундів, що були зіграні, ймовірність випадання сектору №4, який залишився, дорівнює У той же час, для того, щоб випав сектор «Бліц» стрілка може зупинитися на будь якому з 10 секторів. Тобто ймовірність випадання сектору «Бліц» дорівнює Отже, вимога є дійсно обґрунтованою. 

 

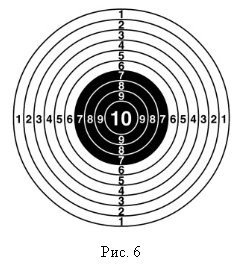Задача 2. При попаданні в центр стандартної мішені, в «10» (наприклад при стрільбі з лука) нараховується відповідно максимальна кількість очок, а саме 10. Усі інші сектори («9», «8», «7» тощо) при віддаленні від центру дають можливість набрати меншу кількість очок. Нас зацікавило математичне пояснення цього факту. Результати міркувань ми обґрунтували за допомогою поняття «геометрична ймовірність» [5].

Розв’язання. Розглянемо стандартну мішень, яка поділена десятьма колами на кільця (Рис.6). Всі кола відстоять одне від одного на  одну і ту ж саму відстань, яку ми позначимо через . Тоді радіус внутрішнього кола, яке відповідає «10» дорівнює ; радіус наступого кола, яке відповідає «9» відповідно радіус кола, яке відповідає «8» відповідно , тощо. Радіус всієї мішені дорівнює .

Ймовірність попадання в «10» дорівнює відношенню площі маленького круга до площі великого круга, тобто

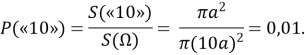
Обчислимо ймовірність попадання в кільце «9» як відношення площі даного кільця до площі всієї мішені :

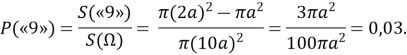
Ймовірність попадання в кільце «8» обчислимо аналогічно :

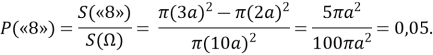
Результати обчислень ми узагальнили у вигляді таблиці (таблиця 3).

Таблиця 3

Зона мішені	10	9	8	7	6	5	4
Ймовірність влучення	0,01	0,03	0,05	0,07	0,09	0,11	0,13

 

Отже, бачимо, що ймовірність попадання в кожний наступний сектор поступово збільшується, що зумовлює зменшення кількості відповідних очок.

Задача 3. Мішень має форму концентричних кругів (Рис. 7). Як мають співвідноситися радіуси кругів, щоб ймовірність влучити у менший круг наближено дорівнювала 50% [5].

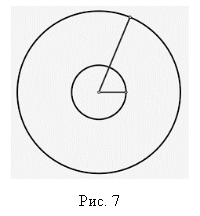Розв’язання. Інтуїтивно можна припустити, що радіуси кругів повинні мати відношення 1:2. Перевіримо цю гіпотезу.

 Обчислимо ймовірність влучення в менший круг. Позначимо радіус маленького круга , а радіус великого круга Тоді відповідна ймовірність дорівнює  .

Радіуси кругів повинні мати відношення 

За умови, що , ймовірність влучення у внутрішній круг буде наближено дорівнювати , що вимагається в задачі. Отже, даний висновок спростовує першу гіпотезу.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Бордуляк М. Т. Теореми і задачі теорії ймовірності: навч. посібн. / М. Т. Бордуляк, О. Б. Скасків, О. М. Сумик, І. Е. Чижиков – Львів: Видавець І. Е. Чижиков, 2013. – 175 с. – (Серія «Математичний практикум»). 
2. Гильдерман Ю.И. Закон и случай/Юрий Гильдерман. – Новосибирск: Наука.-1991.-200 с.
3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. Учеб. пособие для втузов – Изд. 2-е, стер. – М.: «Высшая школа». – 1975. – 333 стр. с илл.
4. Гнеденко Б.В. Из истории науки о случайном.-М.: Знание, 1981.-64 с.
5. Розуменко А.О.. Розуменко А.М. Фахове спрямування курсу теорії ймовірностей при підготовці майбутніх учителів математики // Фізико-математична освіта: науковий журнал. – 2018. – Випуск 1(15), частина 2. – С.67-71
6. Сеньо П. С. Теорія ймовірностей та математична статистика: Підручник. – 2-ге вид., перероб. і доп. – К.: Знання, 2007. – 556 с.