Стаття "Відсоткові розрахунки при розв’язуванні економічних задач "

                                                                           Ольга Овчар, вчитель методист

                                                                              СЗШ №67 м.Львова

   Відсоткові розрахунки при розв’язуванні економічних задач

Стаття написана з досвіду роботи. В даній статті висвітлено питання розв’язування економічних задач на застосування відсоткових розрахунків

Ключові слова: економіка, математика,відсоткові розрахунки.

Article written from experience. In this article the question of solving economic problems on the application of interest payments

Keywords: economics, mathematics, interest calculations.

     Постановка проблеми. . В шкільній програмі є цикл предметів, де відсоткові розрахунки необхідно знати для розв’язування задач з хімії, фізики, біології, економіки.     Розуміння суті відсотків та вміння виконувати відсоткові розрахунки на даний момент є необхідним для кожної людини. Прикладне значення цієї теми дуже важливе, воно стосується багатьох сторін нашого життя (фінансової, демографічної, економічної, екологічної та інших). Однак практика показує, що дуже багато випускників шкіл не мають твердих навиків розрахунку відсотків у повсякденному житті. В шкільній програмі на вивчення і застосування цієї теми відводиться мало часу. Саме тому доцільно надати учням додаткові відомості про використання відсоткових розрахунків на практиці, формувати  розуміння необхідності знання відсоткових розрахунків для вирішення великої кількості задач, продемонструвавши широту використання їх у реальному житті.

       В статті наведені деякі найбільш вживані поняття елементар­ного курсу відсоткових розрахунків. Матеріал має яскраво виражену практичну спрямованість, так як його зміст забезпечує розуміння необхідності та вміння розрахунку відсотків у життєвих ситуаціях.

 

  Мета статті. Ознайомити вчителів із застосуванням відсоткових розрахунків при розв’язуванні економічних задач

      Виклад основного матеріалу.

       При подачі нової теми доцільно повторити і узагальнити теоретичний матеріал,  який ми будемо застосовувати при  опрацюванні та закріпленні практичної частини даної теми.

     Блок ,,А’’. Теорія.

      Первинний процес повторення включає в себе відновлення в пам’яті задач і  формул на розрахунок відсотків. До найпростіших задач на відсотки відносяться:

1.     Знаходження відсотка від даного числа.

(якщо число х становить п% від числа а, то х=) .

2.     Знаходження числа за його відсотком.

(якщо про число х відомо, що його п% дорівнює b, то х=b:).

3.     Відсоткове відношення двох чисел.

(відсоток, який число а0 становить від числа b0, знаходимо за формулою     %).  [3 ]

На наступному етапі навчання подається формула простих відсотків :

 А_п= А₀(1+). І= А₀рn, І= А_п-А₀ - формули дають змогу обчислювати прибуток з капіталу, загальну суму (майбутню, завершену вартість) та основну суму (поточну вартість). А₀ — капітал (основна сума, початкова вартість, поточна вартість, номінальна вартість) — кількість позичених або вкла­дених (інвестованих) грошей, р — відсоткова ставка — нарахування прибутку у вигляді відсотків від основної суми за один рік, А_п — загальна сума (основна сума плюс прибуток, майбутня вартість, завершена вартість) — сума, яка виникла на кінець обумовленого проміжку часу n, І – прибуток, ціна, яку треба сплатити за використання грошей.

  Слід мати на увазі, що прості відсотки використо­вуються переважно у короткочасних фінансових опе­раціях.

  Блок ,,В’’. Теорія.

  Для обчислення складних відсотків вивчаємо формулу:

А_п =  А₀ (1+)ⁿ,  де  р — відсоткова ставка за певний період, п — загальна кількість періодів нарахувань,  А₀ — початковий капітал — кількість вкладених або позичених гро­шей, А_п  — нарощений капітал — сума, яка утвориться на кінець обумовленого проміжку часу. Період — це проміжок часу між двома послідовними нарахуваннями грошей. Нарахування складних відсотків можна здійсню­вати щомісяця (12 раз нарік), щоквартально (4 рази на рік), кожного півріччя (2 рази на рік) тощо. Їх називають відповідно, щомісячним, квартальним, піврічним. Проміжок часу між двома послідовними підрахунками вартості грошей називають конверсійним періодом.

Блок ,,С’’. Теорія.

Для факультативного опрацювання доцільно ознайомити учнів з використанням формули, яка застосовується, якщо кожного разу відсотковий приріст різний -

 А_п = А₀(1+)(1+)…(1+) .

Для закріплення теми задачі також згруповано у блоки.

Блок ,,А’’.

Задачі для осмислення набутих знань з теми ,,Формула простих відсотків’’.

  Задача 1.( Тема ,,Банк і банківська система’’. Завдання на розрахунок прибутку емітента.)  Емітент відкрив депозит у розмірі 2 000 грн. у банк під виплату 18% річних. Яку суму він одержить через 10 місяців.

  Розв’язання. 1 спосіб. Відсоткова ставка р ==1,5% за місяць.

А_п=2 000(1+ )=2 300 (грн).

2 спосіб. За умовою р=18%, n=. А_п=2000(1+)=2 300 (грн).

Відповідь. Емітент одержав 2 300 гривень.

Задача 2. (Тема ,,Кредитні відношення’’. Завдання на розрахунок кількості грошей кредиту.)  Клієнт сплатив банку 100 грн. відсотко­вих платежів за кредит, наданий на 10 місяців під 0,1% річних. Яку суму грошей отримав клієнт цього банку як кредит?

 Розв'язання. За умовою I =100 грн.,  р= 0,1, n= 10 місяців =року = року. Суму грошей обчислимо за формулою: А₀ =, А₀ =    = 1 200(грн). Відповідь. Клієнт отримав у банку кредит 1 200 грн.

 Задача 3. (Тема  ,,Інвестиція’’.  Завдання на розрахунок кількості грошей, необхідних для здійснення інвестиційної діяльності.)  Яка повинна бути сума початкового вкладу при відкритті депозиту за умови виплати 20 % річних, щоб одержати прибуток у

20 000 грн. через: а) 5 роки; б) 9 місяців. 

 Розв'язання. За умовою А_п = 20 000 грн., р == 0,2 ,

а) n=5 років, А₀===10 000 (грн).

б)  n==0,75 року, А₀==17 391,30 (грн).

Відповідь, а) 10 000грн.; б) 17 391,30 грн.

    Задача 4. ( Тема ,,Банк і банківська система’’. Завдання на розрахунок прибутку емітента.)   Під який відсоток емітент відкрив у банку депозит у розмірі 5000 гривень на 10 місяців, одержавши прибуток у сумі  6000 гривень.

       Розв'язання.  За умовою А_п=6000 грн., А₀=5 000 грн., n=10 місяців =

    =року= року . р===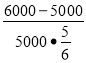0,24;    р=24%.

Відповідь. Емітенту потрібно відкрити депозит під 24%.

Задача 5. ( Тема ,,Банк і банківська система’’. Завдання на розрахунок прибутку емітента.)  На який термін потрібно відкрити депозит у розмірі 10 000 гривень під 15% річних, щоб отримати прибуток 16000 гривень.

 Розв'язання. За умовою А_п=16 000 грн., А₀=10 000 грн., р=15%=0,15.

  n===4 (роки).

Відповідь. Потрібно відкрити депозит на 4 роки.

Задача 6. ( Тема ,,Банк і банківська система’’. Завдання на розрахунок прибутку банку.)   Банк відкриває депозити на умовах виплати 12 % річних і надає кредити на умовах оплати позичальникам під 18 % річних. Яким буде прибуток від      банківських операцій, якщо сума депозитів становить  20 млн. грн., а розмір кредиту 15 млн. грн. у рік?

Розв'язання.   18%=0,18;  12%=0,12.

 15 000 0000,18 – 20 000 0000,12=2 700 000-2 400 000=300 000 (грн).

 Відповідь. Банківський прибуток становить 300 000 гривень.

Задача 7. (грошовий обіг)

    Вирахувати співвідношення купівельної спроможності злотого і національної грошової одиниці, якщо в споживчий кошик входять три продукти – А, Б, В у кількостях 10, 20, і 40, а ціни на них подані нижче:

Ціна в гривнях	20	12	5
Ціна в злотих	7,2	6,52	1,5

Купівельна спроможність грошової одиниці визначається співвідношенням сум у національних валютах для   придбання одиниці товару із запропонованого набору,  який входить до споживчого кошика в  кожній із країн. [4]

На споживчий кошик потрібно:

В гривнях 20 · 10+12 ·20+5 ·40=640.

В злотих: 7,2 ·10+6,52 ·20+1,5 ·40=262,4.

Відношення злотого до гривні:  за 1 гривню – 0,41 злотих.

Відношення гривні до злотого: за 1 злотий – 2,4 гривні.

    Задача 8. (Тема ,,Безробіття’’. Завдання на визначення безробіття.)  Населення Львівської області за даними Головного управління статистики у Львівській області станом на 1.01.2010 року становить 2549,6 тис. осіб. З них дітей до 16 років – 428 068,  людей, що знаходяться в психіатричних клініках і місцях ув’язнення, - 18 353, пенсіонерів – 563 237, безробітних –4 000. Визначити рівень безробіття в області. [7 ]

    Розв'язання. 2 549 600-(428 068+18 353+563 237)= 1 539 942 – робоча сила.

=0,26%   - рівень безробіття.

    Задача 9.  ( Тема ,,Банк і банківська система’’.)  У банку ,,А’’ відкрито депозит на суму, яка становить 30% від суми депозиту у банку  ,,Б’’, а сума депозиту банку ,,Б’’ становить 55%  від суми депозиту вкладеного в банк ,,В’’, а в банку ,,В’’ відкрито депозит, на рахунку якого знаходиться сума ,  яка перевищує депозит у банку  ,,А’’ на 8350 гривень. На яку загальну суму відкрито депозити у трьох різних банках?

 Розв'язання. Нехай х гривень – сума депозиту у банку  ,,В’’. Тоді у банку  ,,Б’’     

 потрібно відкрити депозит на суму 0,55х гривень, а в банку  ,,А’’ –   

 (0,30,55х=0,165х)грн. За умовою х-0,165х=8350, 0,835х=8350, х=10 000(грн) -     

сума депозиту в банку ,,В’’. 0,5510 000=5 500(грн) - сума депозиту в банку ,,Б’’, 0,16510 000=1650(грн). Загальна сума, на яку відкрили депозити у трьох банках, становить 10 000 + 5 500 + 1 650=17 150(грн).

Задача 10. (Тема ,,Фінансові інструменти’’. Завдання на розрахунок дохідності.) Інвестор отримав облігацію номінальної вартості 3 200 грн зі строком погашення 3 роки та відсотковою ставкою 10% річних. Який прибуток отримає інвестор:

1.     Через три роки;
2.     Якщо через рік він продасть її за ринковою вартістю 3 750? [4]

Розв'язання. 1. 10%=0,1, 3 2000,1=320( грн) за 1 рік. За 3 роки – 960 (грн)

1.     3 750-3 200=550 (грн). 550+320=870 (грн) .

   Задача 11. (Тема ,,Фінансові інструменти’’. Завдання на розрахунок дохідності.) Ви маєте суму в 1000 гривень, яку хочете розмістити з метою отримання найбільшого доходу. Банк залучає кошти клієнтів на депозитні вклади під 8% річних; акціонерне товариство випустило цінні папери у вигляді 8 привілейованих акцій номінальною вартістю 250 гривень з виплатою дивідендів у розмірі 10% та 10 звичайних акцій номінальною вартістю 200 гривень. На виплату дивідендів акціонерним товариством відведено 800 гривень. Куди краще вкласти гроші:

1.     у банк;
2.     у привілейовані акції;
3.     у звичайній акції?

Розв'язання. 1) Якщо внести гроші на депозитний рахунок у банк, то через рік можна отримати 80 гривень у вигляді нарахованих та виплачених банком доходів.

2) Дивіденди на привілейовані акції складуть 810%=80% , тобто 80% від 800 складає 640 грн. Одна привілейована акція дає прибуток 80 грн. За 1000 грн. можна купити 4 акції по 250 грн. Прибуток буде 320 грн.

3) На виплати по звичайних акціях залишиться 800-640=160 (грн). А виплачені дивіденди на звичайну акцію становить 160:10=16(грн). Звичайних акцій можна купити 1000:200=5 і отримати прибуток 516=80(грн). Отже, найкраще придбати привілейовані акції акціонерного товариства.

Блок ,,В’’.      Задачі на використання формули складних відсотків.

Задача 12. ( Тема ,,Банк і банківська система’’. Завдання на розрахунок прибутку емітента.)  У день народження сина його батьки відкрили депозит у сумі 1000 грн. у банку під виплату 18 % річних із щорічним нарахуванням складних відсотків. Яка сума грошей буде на цьому рахунку, коли сину виповниться 20 років?

Розв'язання. За умовою задачі А₀ = 1000 грн., р = 18 % = 0,18, n = 20. Тому

А_п=1000(1+0,18)²⁰=1000·27,393=27393(грн). Отже, на рахунку буде 27 393 грн.

Задача 13. ( Тема ,,Банк і банківська система’’. Завдання на визначення початкової суми депозиту.)   Яким повинен бути початковий вклад для відкриття депозиту у банку на 5 років при умові виплати 20 % річних за умови піврічного нараху­вання складних відсотків для того, щоб загальна сума на рахунку наприкінці п’ятого року склала 15 000 грн.?

Розв'язання. ,     P=5783 (грн).

Відповідь. У банк слід покласти 5783 грн.

 Задача 14. ( Тема ,,Банк і банківська система’’. Завдання на визначення початкової суми депозиту.)  За 4 роки початкова сума вкладу, при виплаті 18 % річних при щоквартальному їх нарахуванні,  досягла 10000 грн. Знайти початкову суму вкладу.

Розв'язання. За умовою р = 18 % = 0,18 – річна ставка, n =4· 4=16, А_п=10 000 грн. р==0,045 – ставка відсотка за конверсійний період

А₀ =4 944,69 (грн)

Відповідь. ≈4 944,69 грн.

Задача 15. ( Тема ,,Банк і банківська система’’. Завдання на розрахунок прибутку емітента.)   Три емітенти розмістили гроші в банку під 12% річних. Скільки через рік отримає кожний з них при умові, що сума вкладу кожного власника депозиту 1000 у.од., якщо перший прийде через рік, другий зніме й вкладе всю суму з нарахованими відсотками через півроку, а третій – раз у квартал?

Розв'язання.

1.     Перший, знявши через рік отриману суму, отримає 1120 у.од.
2.     Другий емітент, знявши гроші через півроку, отримає 1060 у.од.. Поклавши їх назад, через наступних півроку отримає 1123,6 у.од. або за формулою складних відсотків   1000 ·(1+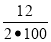)²=1123,6 (у. од.)
3.     Третій емітент отримає:1000·(1+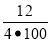)⁴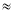1125,51(у.од.).

    Задача 16. ( Тема ,,Банк і банківська система’’. Завдання на розрахунок прибутку банку.)  Клієнт позичив у банку 50 000 грн. Банк надав кредит під 10 % при щоквартальному їх нарахуванні. Через 5 років боржник сплатив позику одноразовою сумою.

а) Знайти суму одноразової сплати.

б) Знайти прибуток банку.

Розв'язання. Оскільки р = 10 %, т = 4, то  р′ =0,025 .

Загальна кількість періодів п =5 ·4=20

Тоді А_п=50000 ·1,025²⁰81930,8( грн), що становить суму одноразової сплати.   

Тоді прибуток банку дорівнює: 31930,8 грн.

Задача 17.  ( Тема ,,Банк і банківська система’’.)  На початку року є можливість внести в банк на рахунок 1640 гривень. Але в кінці року треба зняти з рахунку 882 гривні, а через рік знову –882 гривні. Під який відсоток потрібно внести гроші в банк, щоб вказані операції відбулися?[2]

Розв'язання. Нехай х% - щорічні відсоткові нарахування. Тоді на кінець року банк нарахував (0,01х1640) грн. і на рахунку в кінці року стало (1640+0,01х1640)грн., або (1640(1+0,01хНа початку другого вклад становив (1640(1+0,01хгрн. Відсоткові гроші, нараховані на цю суму становлять (0,01хгрн. А сума, яка була нарахована в кінці другого року становить ((1640(1+0,01хгрн., що за умовою становить 882 гривні.

Отримаємо рівняння: (1640(1+0,01х)-882)(1+0.01х)=882. Введемо змінну у=1+0,01х. Тоді рівняння має вигляд: 1640у²+882у-882=0, звідси у₁= - не задовольняє умови задачі,  у₂=.  Тому 1+0,01х=, а х=5%

Блок ,,С’’.     Розрахунок рівня інфляції

Задача 18.     Вкладник поклав певну суму на рік під 20% у банк, в зв’язку з кризою через рік банк знизив відсоткову ставку до 15%. На який відсоток зросте початковий внесок емітента?

Розв'язання.  А₀=х грн. Тоді х(1 +) (1 +)=1,38х, що становить % =138% від початкової суми, тобто початковий внесок зросте на 38%.

    Задача 19.

Петренко відкрив депозит на три роки. Договір передбачає наступну схему нарахування відсотків: за перший рік – 10%, а за кожний наступний ставка підвищується на 2%. Визначити на скільки відсотків зросте депозит Петренка за три роки?

    Розв'язання.  А₀=х грн. Тоді х(1 +) (1 +) (1 +) 1,40 х, що становить % =140% від початкової суми, тобто початковий внесок зросте на 40%.

 Висновок.

    Розв’язування запропонованих задач економічного характеру на відсоткові

 розрахунки ознайомлюють учнів з застосуванням формул відсоткових

розрахунків у сфері фінансів та банківській справі, розкривають можливості

математики у економічній теорії, сприяють розвитку та активізації математичного мислення, зацікавлюють учнів у вивченні даних предметів, озброюють їх знаннями щодо здійснення операцій з фінансовими інструментами, стимулюють самостійне опрацювання додаткових джерел та засобів Інтернет ресурсу. Завдяки цьому мотиваційна наповнюваність навчального процесу розширює спектр поповнення пізнавальної діяльності учня та сприяє оптимізаційному розвитку їх розумових та творчих здібностей. Таким чином основне завдання навчального процесу по формуванню креативної особистості учня досягається в основному за рахунок розвитку логічного мислення, яке повинно включати в себе уміння поетапного моделювання розв’язку задачі, тобто

1.     виявлення тематичної спрямованості задачі (розкриття сутності

взаємозв’язку між економічною темою та вибором моделі розв’язку задачі).

2.     визначення етапів розв’язання даної моделі.
3.     вести пошук альтернативної ідеї розв’язування задачі

за допомогою засвоєних формул.

   4)  створення раціональної схеми розв’язування запропонованого завдання з метою оптимізації обсягів отриманого прибутку.

     Задачі можна використати  для індивідуальної роботи, факультативних і гурткових занять.

1.     Лисенко В.І. Економічні задачі у загальноосвітній школі.

/Ю.І.Пономаренко. Газета ,,Математика’’, №21 (225), червень 2003, ст.13-19.

2.     Межейнікова Л.С. Математичні задачі з фінансовим змістом в основній школі./ В.О.Швець. - Харків. Видавнича група ,,Основа’’, 2005. – ст.13.
3.     О.Істер.  Повний курс підготовки до вступних іспитів. - Київ. Видавництво А.С.К., 2007. – ст.42-48.
4.     Мірясов Ю.О. Основи економіки. Відповіді на питання екзаменаційних білетів державної підсумкової атестації 2002. – Харків. Видавництво,,Ранок’’, 2002. – ст.35
5.     Кошколда  І.В. 334 задачі з економіки з розв’язками. /В.П.Щербань. – Харків. ,,Гімназія’’, 2008.
6.     http://www.stat.lviv.ua/  Головне управління статистики у Львівській області.