Урок на тему "Числові послідовності. Арифметична прогресія."
Тема: Числові послідовності. Арифметична прогресія.
Мета: закріплення знань; формування вміння використовувати означення і формули п-го члена та суми п перших членів арифметичної прогресії під час розв'язування вправ; розвиток логічного мислення.
Тип уроку. Урок формування вмінь і навичок.
Хід уроку
I. Організаційний момент.
Учитель повідомляє тему і мету уроку та здійснює мотивацію навчально-пізнавальної діяльності учнів.
II. Перевірка домашнього завдання.
1. (1-й варіант)
Знайдіть суму п'ятнадцяти перших членів арифметичної-прогресії, якщо її третій член дорівнює -5, а шостий дорівнює 2,2.
Розв'язання
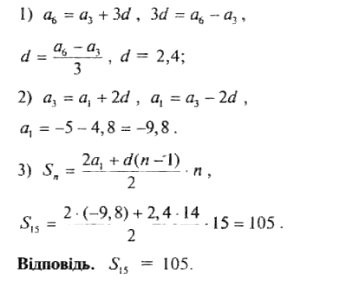
2. (2-й варіант). Скільки від'ємних членів має арифметична прогресія —28; —25; —22; ...?
Розв'язання
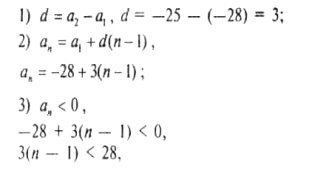
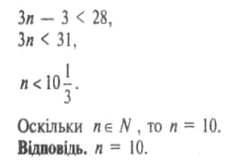
3. (3-й варіант).
Знайдіть перший член арифметичної прогресії, різниця якої дорівнює 15, а сума її перших тринадцяти членів дорівнює 1326.
Розв'язання
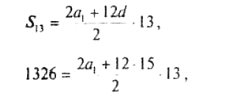
102 = а1 +6 15,
а1 =102-90, а1 =12.
Відповідь, а1 = 12.
III. Індивідуальна робота за картками.
1. Дано арифметичну прогресію —22,5; —21; ... Знайти 11-й член і різницю прогресії.
Розв'язання
- а1 = -22,5, а2 = -21, d = аг-а1,
d =-21 - (-22,5) = 1,5;
- а11 = а1 + 10d,
а11 =-22,5+ 10 ∙1,5 = -22,5+ 15 = -7,5.
Відповідь: d= 1,5, а11 = -7,5.
2. Знайти перший член і різницю арифметичної прогресії (ап), якщо а4 =1,8, а7 =0,6.
Розв'язання
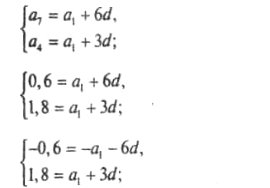
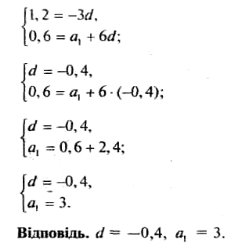
IV. Гра «Хто сильніший».
Учням пропонується дати відповіді на теоретичні та практичні запитання. Якщо учень відповідає на запитання неправильно, то воно переходить до наступного учня. Учні мають змогу збільшити кількість балів протягом уроку. Така гра стимулює учнів до своєчасного вивчення теоретичного матеріалу та подальшої активної роботи на уроці.
Запитання
- Сформулювати означення арифметичної прогресії.
- Що називають різницею арифметичної прогресії?
- Які бувають арифметичні прогресії?
- Яка арифметична прогресія є спадною?
- Яка арифметична прогресія є зростаючою?
- Назвіть формулу п-го члена арифметичної прогресії.
- Що потрібно знати, щоб знайти суму 10 перших членів арифметичної прогресії?
- Запишіть формули суми п перших членів арифметичної прогресії:
- Які з наведених нижче послідовностей є арифметичними прогресіями:
- 17; 17; 17; ...
- 100; 101; 104; ...
- -7; -8; -9; ...
- -5; 10; -15; ... ?
- Знайдіть різницю арифметичних прогресій з попереднього пункту.
- Знайдіть чотири перших члени арифметичної прогресії, у якої а1 = 5, d = 2.
- Чи можуть члени арифметичної прогресії 1000; 1000,1; 1000,2; ... стати:
- меншими ніж —3001;
- більшими ніж 3001?
13. Як знайти суму членів даної арифметичної професії з п'ятого по десятий
члени?
V. Гра «Мовчанка».
Перевірку вміння застосовувати теоретичний матеріал на практиці можна провести у формі гри «Мовчанка». На дошці записано початок твердження і кілька варіантів відповідей. Учитель почергово вказує на різні варіанти твердження (наприклад, 1а, 1б, 1в тощо), а учні, які вважають його хибним, повинні підняти руку. Це дозволяє перевірити засвоєння матеріалу всіма учнями класу та сприяє його більшій організованості.
Запитання
1. Дано скінченну послідовність 1; 3; 4; 5; 6.
а) Другий член даної послідовності дорівнює 4;
б) різниця між другим і першим членом цієї послідовності дорівнює 2;
в) кожний наступний член даної послідовності можна одержати з попереднього, додавши до нього число 2;
г) дані числа є послідовними членами деякої арифметичної прогресії.
2. Відомо, що в арифметичній прогресії а1 = 5, а різниця d = 3.
а) другий член даної прогресії дорівнює 5;
б) третій член даної прогресії дорівнює 18;
в) третій член даної прогресії дорівнює 11;
г) а3-а2=5
3. Формула п-го члена арифметичної прогресії:
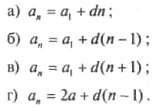
4. Формула суми п-го члена арифметичної прогресії:
![]()

VI. Розв'язування вправ.
1.Перший член арифметичної прогресії дорівнює 2, а її різниця дорівнює 5.
Скільки треба взяти перших членів прогресії, щоб їх сума дорівнювала 156?
Розв'язання
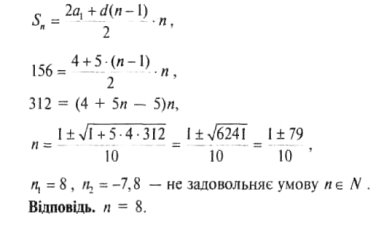
2. Знайдіть суму всіх від'ємних членів арифметичної прогресії
—5,2; —4,8; —4,4; ...
Розв'язання
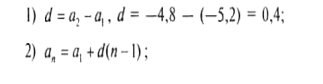
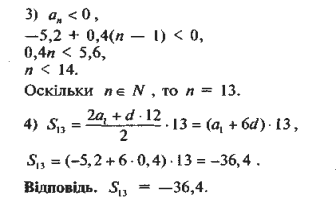
3. При будь-якому п сума п перших членів деякої арифметичної прогресії
Sп = Зп2 + 5п. Знайдіть три перших члени цієї прогресії.
Розв'язання
Перший спосіб
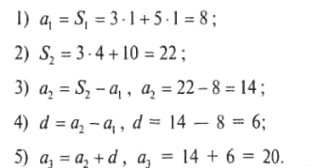
Другий спосіб
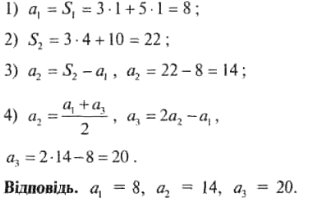
VII. Індивідуальні додаткові завдання.
1. Знайдіть суму всіх натуральних чисел, менших від 700, які кратні 8.
Розв'язання
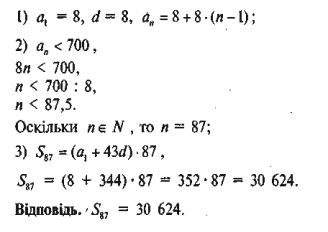
2. Знайдіть різницю арифметичної прогресії, перший член якої дорівнює —16, а сума її перших сімнадцяти членів дорівнює 544.
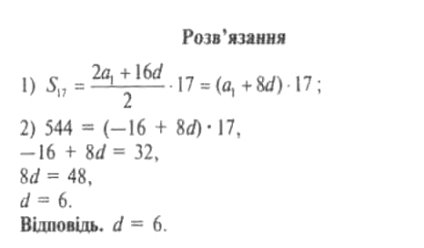
VIII. Самостійна робота.
1. Знайдіть суму десяти перших членів арифметичної прогресії
![]()
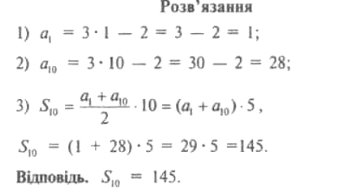
2. Знайдіть суму восьми перших членів арифметичної прогресії (хп), якщо хз = —4, х5 = 2.
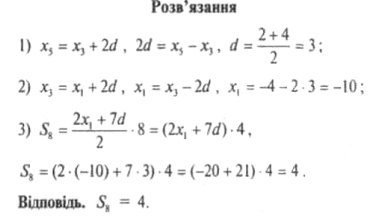
IX. Гра «Розшифруй слово».
На кожну парту роздаються картки із запитаннями. Учням пропонується вибрати, під якою буквою знаходиться правильне твердження і з послідовності вибраних букв утворити слово. (Це буде слово «теорема».)
1. Означення арифметичної прогресії.
т) арифметичною прогресією називають послідовність, кожен член якої, починаючи з другого, дорівнює попередньому члену, до якого додається одне й те саме число.
о) арифметичною прогресією називають послідовність, кожен член якої, починаючи з другого, дорівнює попередньому члену, помноженому на одне й те саме число.
2. Відомо, що в арифметичній прогресії перший член дорівнює а1 =7, а різниця d=2.
ж) Різниця між третім і другим членами даної прогресії дорівнює 5;
е) третій член даної прогресії дорівнює 11.
3. Дано арифметичну прогресію з першим членом 5 і другим членом 10.
м) Різниця даної прогресії й = — 5; о) сума чотирьох перших членів цієї прогресії
дорівнює 50.
4. Дано зростаючу послідовність усіх двоцифрових чисел, кратних 7.
р) Дані числа утворюють арифметичну прогресію з різницею 7;
є) у даній послідовності перший член дорівнює 7, третій член дорівнює 21.
5. Між числами 5 і 105 слід вставити три числа так, щоб вони разом з даними числами утворювали зростаючу арифметичну прогресію.
д) Число 80 буде третім членом цієї прогресії;
е) число 80 буде четвертим членом прогресії.
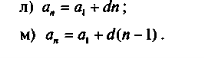
7. Формула суми п перших членів арифметичної прогресії:
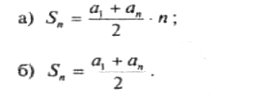
6. Формула п-го члена арифметичної професії:
X. Домашнє завдання.


про публікацію авторської розробки
Додати розробку
