Стаття "Застосування похідної до розв’язування ірраціональних рівнянь"

                             Застосування похідної до розв’язування

ірраціональних рівнянь

Математика як і інші предмети навчального плану закладу освіти має на меті розвиток загального інтелектуального рівня, спеціалізованої математичної підготовки, розвитку творчого підходу до розв’язання поставлених як вузькопрофільних так і життєвих питань.

Готуючи здобувачів освіти до зовнішнього незалежного оцінювання з математики,  зустрічаємося зі значним обсягом рівнянь, які потрібно виконати за обмежений проміжок часу. Досить часто при розв’язуванні рівнянь зустрічаються такі рівняння, де потрібно застосувати не стільки технічні навички їх розв’язування, скільки уважність, уміння знайти найкоротший шлях розв’язання, застосовувати нетрадиційний, оригінальний метод тощо.

Досвід роботи свідчить, що практика розв’язання рівнянь має широкі можливості по формуванню інтуїції,  підвищення практичних прийомів логіки мислення. Серед таких тем – тема ірраціональні рівняння. Цікавим моментом при цьому є саме застосування нестандартних підходів до їх розв’язання. Серед таких прийомів -  застосування похідної. Цей прийом варто показувати після прийому застосування монотонності функцій до розв’язування ірраціональних рівнянь з обов’язковим формулювання теорем про кількість коренів рівнянь монотонних функцій. 

       Скористатися цими теоремами для встановлення монотонності заданих функцій  буває нелегко, а іноді і неможливо. Тому в цьому випадку доречно скористатися похідною функції для встановлення монотонності функцій.

Приклад 1.  Розв’язати рівняння

                                          –

Розв’язання.

ОДЗ:

          Шляхом добору очевидно, що число 8 є коренем рівняння. Доведемо, що він єдиний.

Маємо, зростає і неперервна, а спадає і неперервна на області визначення.  Встановимо монотонність функції

Знайдемо похідну функції

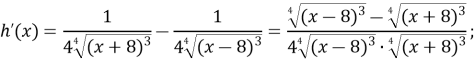
   Оскільки знаменник похідної функції – число додатнє на області визначення, а чисельник – число від’ємне, тому на всій області визначення. Робимо висновок, що   спадає  і неперервна на області визначення, тому рівняння

                                          –

має один корінь.

Відповідь:  8.

Приклад 2. Розв’язати рівняння

=

Розв’язання.

ОДЗ: 2

         Встановити монотонність функцій у рівнянні неможливо, тому скористаємося допомогою похідної.

Нехай тоді

  - ; 

Знайдемо значення функції в цій критичній точці та на кінцях інтервалу

Значить, 

Проте, а, значить, рівність

= 

можлива лише при виконанні умови

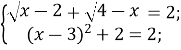
Звідки

Шляхом підстановки числа 3 у початкове рівняння впевнюємося, що 3 є коренем рівняння.

Відповідь: 3.

Приклад 3. Розв’язати рівняння

Розв’язання.

ОДЗ:

          Загальний вигляд рівняння спонукає до застосування методу оцінки правої та лівої частин рівняння. Оскільки не дозволяє зробити висновок про відсутність коренів чи перейти до рівносильної системи рівнянь, здійснимо перевірку кінцевих точок проміжку на предмет коренів.

При

При

Наявність інших коренів чи їх відсутність доведемо із застосуванням похідної.

Позначимо  

Знайдемо її похідну.

+ ;

 якщо

Одержаний корінь належить області визначення; він розбив її на два проміжки: Установимо знак похідної на кожному з них.

          Значить, на проміжку функція      

є зростаючою і неперервною, тому  -  єдиний корінь на цьому проміжку.  Аналогічно, функція     на проміжку

  спадає і неперервна, тому число  1 – єдиний корінь на цьому проміжку.

Відповідь: -15;  1.

Приклад 4.    Розв’язати рівняння

Розв’язання.

ОДЗ: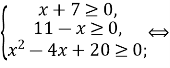

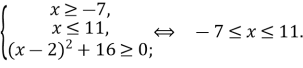
Розглянемо функції

Визначимо їх проміжки монотонності, а якщо цього буде не досить для визначення коренів заданого рівняння  -  їх найбільше (найменше) значення.

   якщо     звідки       

Число 2 належить визначеній області визначення та розбиває її на два проміжки     і

Визначимо знаки похідної функції на кожному з цих проміжків.

       Значить, функція

неперервна на області визначення і є спадною на проміжку та зростаючою на проміжку     Тому   є точкою максимуму функції на проміжку .

 max.

         Встановимо найменше значення функції  З цією метою визначимо її значення на кінцях проміжку .

min

Тепер розглянемо функцію  

       Визначимо координати вершини параболи

 y=х₀=2,        у₀= 16.

       Скористаємося методом оцінки, виділивши повний квадрат підкореневого виразу. Одержимо

= 3=6.

Тобто, на області визначення min

Значить, max при

Отже, число 2  -  єдиний корінь заданого рівняння.

Відповідь: 2.

          Розглянемо ще декілька типів рівнянь, в яких використовуються похідні. Серед них рівняння, в яких потрібно вияснити, чи має розв’язок те чи інше рівняння. Ці рівняння зводяться до знаходження екстремальних значень функції або до знаходження їх областей значень.

 Приклад 5.    При якому значенні має розв’язки рівняння:

                               + 

Розв’язання.

Область визначення даного рівняння – інтервал . Розглянемо на ній функцію :

Тоді на інтервалі

      =

;              .

         Так що    – єдина критична точка функції , яка до того ж є точкою максимум, оскільки ) = 2 = , = .    Отже приймає найбільше значення при x= а найменше значення – при . Так як функція неперервна, то її область значень є інтервал між її найбільшим і найменшим значенням, тобто дане рівняння має розв’язок , якщо .

 Відповідь:  .

Приклад 6.   Скільки коренів має рівняння:        

 Розв’язання.

            Область визначення даного рівняння – інтервал . Розглянемо на цьому інтервалі функцію

,   тоді

- .

- ;

.

              Враховуючи область визначення, маємо . Таким чином, функція зростаюча, так що дане рівняння не може мати більше одного кореня. З іншого боку, взявши будь – яке велике значенняx наприклад, маємо:

 так що як неперервна функція приймає всі значення між , в тому числі і значення 4.

 Відповідь. Рівняння має лише 1 корінь.

Доцільно знати (методичні поради ).

Визначення зростання (спадання) функції.

• Одним із шляхів є знаходження похідної функції та застосування властивості похідної функції щодо зростання (спадання) функції.
• Для елементарних функцій, що вивчаються в шкільному курсі математики, слід мати на увазі наступне:
  • Якщо функція 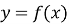зростає на деякому числовому проміжку, то функція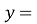 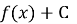також зростає на цьому проміжку.
  • Якщо функція 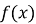зростає на деякому числовому проміжку, то функція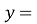 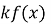є зростаючою на цьому проміжку при 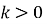та спадною при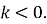 
  • Якщо функці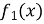ї і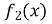зростають (спадають) на числовому проміжку, то функція 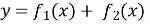також зростає (спадає) на цьому проміжку.
  • Якщо функці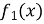ї і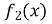зростають на числовому проміжку, то функція 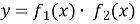також зростає на цьому проміжку.

• Для складних функцій:

• Зростаюча від зростаючої функції є зростаюча, і спадна від спадної  - також зростаюча (на зразок множення чисел з однаковими знаками).
• Зростаюча від спадної функції і спадна від зростаючої є функція спадаюча (на зразок множення чисел з різними знаками).

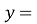
• Якщо функція 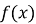зростає (спадає) на деякому числовому проміжку і не дорівнює нулю на ньому, то функція y = 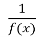 спадає (зростає) на цьому ж проміжку.

        Якщо ОДЗ рівняння складається з окремого числа та проміжку, знаходження коренів заданого рівняння зводиться до:

• Перевірки значення окремого числа на можливість його як кореня заданого рівняння;
• Оцінки лівої та правої частин заданого рівняння на проміжку

для встановлення наявності коренів на цьому проміжку чи їх відсутності.