STEM- ІГРАШКИ: ФЛЕКСАГОНИ ТА ФЛЕКСЕРИ.
УПРАВЛІННЯ ОСВІТИ
РІВНЕНСЬКОГО МІСЬКОГО ВИКОНАВЧОГО КОМІТЕТУ
РІВНЕНСЬКИЙ МІСЬКИЙ ЦЕНТР ТВОРЧОСТІ УЧНІВСЬКОЇ МОЛОДІ
Ходневич Олена Федорівна
Методичні рекомендації
STEM- ІГРАШКИ: ФЛЕКСАГОНИ ТА ФЛЕКСЕРИ


Рівне – 2020
Зміст
Вступ…………………………………………………………...…2
1. Історія відкриття…………………..………………..…………….4
2. Виготовлення флексагонів……..………………………………..7
2.1. Виготовлення тригексафлексагона……………………….7
2.2. Виготовлення тетрагексафлексагона…………………..…9
2.3. Виготовлення пентагексафлексагона……………………11
2.4. Виготовлення гептагексафлексагона…………………….14
2.5. Виготовлення гексагексафлексагона……………….…….16
3. Шлях Таккермана………………………………………….……..18 4. Виготовлення флексора…………………………………...……..20
4.1. Виготовлення шестикутного флексора ………………….20
4.2. Виготовлення восьмикутного флексора ………………....23
4.3. Виготовлення десятикутного флексора …………….....…24
4.4. Виготовлення дванадцятикутного флексора ………….....25
5. Суперечка про існування флексора……………………………...26
6. Магічне кільце із восьми тетраедрів……………………...…..…27
7. Корисні поради при виготовленні флексагонів та флексорів….28 8. Використання флексагонів і флексорів………………….……...29
Висновки………………………………………………………….31
Література…………………………………………………………32
Додатки……………………………………………………...…….33
Вступ
Всі ми любимо цікаву математику. Цікава математика викликає інтерес, уміння логічно мислити, віру в свої сили. Елементи гри, які роблять цікаву математику насправді цікавою, може мати форму головоломок, фокусів, парадоксів і т. п.
Багато хто вважає, що математика не цікава і містить тільки формули, задачі, рівняння та приклади. В даній розробці містяться матеріали, які можна використовувати на заняттях гуртка початкового технічного моделювання, які розширюють знання з математики, креслення, технологій та історії. Паперові іграшки-головоломки не тільки займуть руки і увагу дитини на довгий час, а й допоможуть розвивати інженерне мислення і математичні навички. Застосування елементів STEАM - освіти під час занять створює додаткову мотивацію до навчання: вихованці добре засвоюють матеріал, тому, що це їм цікаво.
В Атлантичному океані є місце, по формі нагадує геометричну фігуру. Це місце, розташоване між Бермудськими островами, державою Пуерто-Ріко, півостровом Флорида і називається « бермудський трикутник». А ще його називають «трикутник диявола», «трикутник проклятих». Загадковість його полягає в тому, що там безслідно зникають кораблі і літаки. Природа « бермудського трикутника» залишається таємницею і по цей час. Що такого загадкового в трикутнику?
Трикутник «жорстка» фігура. Якщо дано три його сторони, то форму його змінити не можна, не порушивши його. Ця властивість широко використовується на практиці.
У трикутника є просторові «родичі»: тетраедр, октаедр, ікосаедр. Ці геометричні тіла являються «родичами» трикутника тому, що грані цих тіл – трикутники.
«Родичем» трикутника є й геометрична паперова стрічка, так як її поверхня складається з трикутників. Ця іграшка називається флексагон.
Клаптик паперу, здатний зацікавити не тільки дитину, а й дорослих. Для деяких це не просто іграшка-головоломка, а й справжній перший крок в світ математики. Яскраві лінії складеного паперу захоплюють не гірше дитячого калейдоскопа з різнокольоровим склом. Та ще й назва така загадкова – флексагон. Що ж це таке насправді? Дуже часто тема головоломок в школі є складною і незрозумілою, але в деяких дітей це викликає неабиякий інтерес.
Флексагони і флексори – це не просто іграшка, це засіб математичного розвитку учнів. Із року в рік STEM-іграшки набувають все більшої популярності серед дітей та їхніх батьків. Причини цього очевидні: бавлячись з ними, дитина водночас розвивається та навчається.
Отож, запрошую вас на екскурсію у світ флексагонів та флексорів – паперових іграшок, яким властива дивовижна особливість раптово змінювати форму і колір. Такі паперові головоломки можна виготовляти як на заняттях гуртка початкового технічного моделювання так і на уроках математики, а також для STEM-освіти, яка розширює можливості дітей для дослідження світу через подібні творчі проєкти.
Підібрані матеріали допоможуть учням створити власні STEMпроєкти, в яких вони на практиці зможуть застосувати знання з точних наук, проявити творчість та кмітливість!
1. Історія відкриття.
Флексагони були відкриті випадково в кінці 1939 року.
Аспірант-математик із Пристонського університету (США) англієць
Артур Стоун обрізав листок американського блокноту під звичний формат (формат американського блокноту ширше на 18,4мм).

 Звичний формат Американський блокнот
Звичний формат Американський блокнот
Він хотів трохи відволіктись, і почав складати з відрізаних смужок
паперу різні фігури.

Мал.1. Пристонський університет, штат Нью Джерсі
Склавши смужку паперу в трьох місцях під кутом 60 градусів (мал.2), він отримав рівносторонній шестикутник. Склеїв кінці смужки, Стоун отримав фігуру з дуже цікавими властивостями: підгинаючи один з кутів шестикутника до центру, можна швидко відкрити його, як бутон квітки (мал.3).
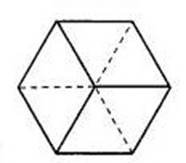
Мал.2. Місця згину смужки паперу для отримання
рівностороннього шестикутника
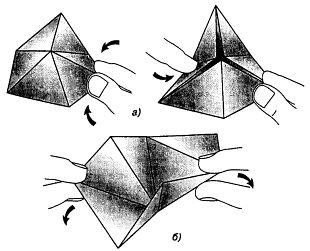
Мал.3. Розкриття шестикутника
Відчувши, що за загадковою фігурою ховається цікава
математична теорія, Стоун продемонстрував свою поробку друзям. Серед них були фізик Річард Фейнман, математик Брайан Таккерман і Джон Тьюкі. Друзі назвали винайдену Стоуном фігуру флексагоном (з англійської flex – складається, згинається, гнеться). Жартома вони назвали себе «Флексагонним комітетом» і взялися за вивчення математичних основ «флексології».
Під флексогонами стали розуміти многокутники, складені зі
смужок паперу прямокутної чи більш складної, зігнутої форми, які мають дивовижну властивість: при згинанні флексагонів їх зовнішні поверхні ховаються в середину, а раніше внутрішні не видимі не очікувано виходять на верх.
До 1940 року Фейтманом і Тьюки була розроблена теорія
флексагонів, яка дозволяла побудувати флексагон з будь-якою кількістю сторін і поверхней різними способами. Повністю ця праця так і не була надрукована, хоча окремі її положення потім були відкриті іншими вченими.

Мал.4. Зліва направо: Артур Стоун, Річард Фейнман, Джон Тьюкі, Брайан Таккерман.
7 грудня 1941 року японці увірвалися у Перл-Харбор і війна розкидала учасників «Флексагонного комітету» по всьому світу. Внаслідок Артур Стоун набув світової слави, як спеціаліст в області топології і автор теореми метризації, названої в його честь. Джон Тьюки отримав титул магістра хімії і докторську ступінь з математики. Він винайшов декілька основоположних методів сучасної статистики. Брайан Таккерман залишив значний вклад в інформатиці, як один із співавторів симетричного алгоритму захисту інформації, в якому один ключ використовується як для шифрування, так і для розшифровування даних. А Річард Фейнман і зовсім не потребує рекомендацій, як власник премії Альберта Ейнштейна і Нобелівської премії в області фізики. Довгі роки ці вчені хотіли знову зібратися разом, щоб написати кілька статей і завершити зі всіма таємницями теорії флексагонів.
На жаль, а можливо, на щастя цьому плану так і не судилося збутися.
2. Виготовлення флексагонів
2.1. Виготовлення тригексафлексагона
Постійні моделі були названі гексафлексагонами: «гекса» - тому що шестикутна форма, «флексагонами» - через властивість складатися. Перший виготовлений Стоуном флексагон був названий тригексафлексагоном, так як у нього були три поверхні.

Інструкція Щоб не заплутатись при складанні тригексафлексагона:
лицева сторона — біла, зворотня — сіра.
1. Вирізаємо шаблон (або креслимо 10 рівносторонніх трикутників).
Надписуємо цифри або розмальовуємо.
2. Зігнути по всіх пунктирних лініях і знову розігнути.
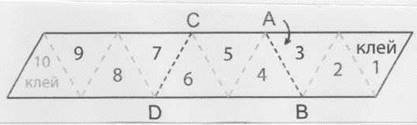
3. Зігнути по лінії АВ, відігнувши 3 трикутники (1-3) вперед.
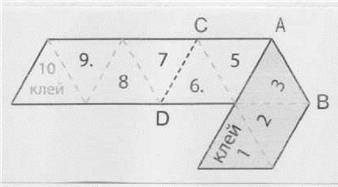
4. Зігнути по лінії CD, відігнувши з другої сторони 4 трикутники (7-10) назад.
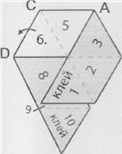
5. Підсунути кутик 1 вниз під 9, відігнути кутик 10 вниз і склеїти 10 з 1 лицевими сторонами.
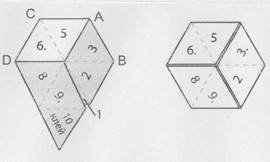

2.2. Виготовлення тетрагексафлексагона
Тетрафлексагон також існує лише в єдиному варіанті. Його складають із «пилкоподібної» смужки і має чотири поверхні.
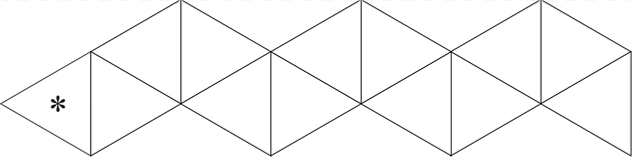
1. Підготувати смужку паперу, поділену на 13 рівносторонніх трикутників ( можна роздрукувати шаблон)
Зробити згини кожної лінії, які ділять смужку на трикутники в обидві сторони, щоб майбутній флексагон легко розкривався. Прономерувати трикутники з однієї сторони цифрами 3,1,2,3 (за зразком)
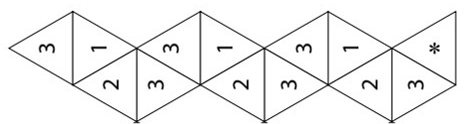
Перевернути цю смужку і пронумерувати трикутники на зворотній стороні цифрами 4,4,1,2. * – позначено трикутник який буде склеюватись.
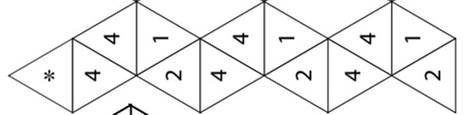
2. Скласти смужку так, щоб трикутники зі зворотної сторони, які мають одинакові номери (з цифрами 4) опинились накладені один на одного.

3. Скласти смужку так, щоб трикутники, які мають одинакові номери (з цифрами 1) опинились накладені один на одного.

4. Залишається лише підігнути кутик з зірочкою вниз і приклеїти його до іншого трикутника з зірочкою на нижній стороні смужки. Якщо все виконано вірно, то на всіх трикутниках видимої сторони шестикутника повинна стояти цифра 3, а на всіх трикутниках на зворотній стороні – цифра
2.

2.3. Виготовлення пентагексафлексагона
Пантофлексагон має п’ять поверхней. Єдиний різновид цього флексагона складають зі смужки, що зображена на малюнку.

1.Підготувати смужку паперу, розподілену на 16 рівносторонніх трикутників ( можна роздрукувати шаблон).
2.Зробити згини кожної лінії, які ділять смужку на трикутники в обидві сторони, щоб майбутній флексагон легко розкривався.
3.Прономерувати трикутники з однієї сторони цифрами
1,2,3,1,2,4,4,5,5,3,1,2,3,1

Перевернути цю смужку і прономерувати трикутники на зворотній стороні цифрами 3,5,5,4,4,2,1,3,2,1,3,5,5,4,4,2.

4.Скласти смужку так, щоб трикутники зі зворотної сторони, які мають одинакові номери (з цифрами 5) опинились накладені один на одного. В результаті вийде ось така смужка.

5.Скласти смужку так, щоб трикутники, які мають одинакові номери (з цифрами 4) опинились накладені один на одного.

6.Скласти смужку так, щоб трикутники, які мають одинакові номери (з цифрами 3) опинились накладені один на одного.

7.Залишається лише підігнути трикутник з зірочкою вниз і приклеїти його до іншого трикутника з зірочкою на нижній стороні смужки. Якщо все виконано вірно, то на всіх трикутниках видимої сторони шестикутника повинна стояти цифра 1, а на всіх трикутниках на зворотній стороні цифра
2.

Згинаючи гексагексафлексагон, можна побачити всі п’ять його поверхней.
2.4. Виготовлення гептагексафлексагона.
Інший, на менш цікавий флексагон отримав назву гептагексафлексагон
( перше «гепта» - сім- це значить кількість поверхней цієї моделі) .
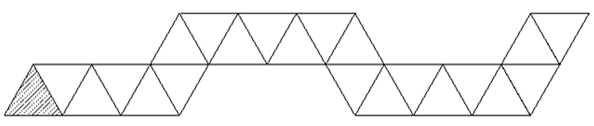
1. Підготувати смужку паперу, розподілену на 22 рівносторонніх трикутників ( можна роздрукувати шаблон).
2. Зробити згини кожної лінії, які ділять смужку на трикутники в обидві сторони, щоб майбутній флексагон легко розкривався.
3. Прономерувати трикутники з однієї сторони цифрами
1,2,3,1,2,7,7,6,4,4,5,5,6,3,1,2,3,1,2,7,7,6

Перевернути цю смужку і прономерувати трикутники на зворотній стороні цифрами х,4,4,5,5,6,3,1,2,3,1,2,7,7,6,4,4,5,5,6,3,х, де х- місце нанесення клею.

Як варіант, можна замість цифр розфарбувати в різні кольори ( кожній цифрі відповідає тільки один колір)
4. Скласти смужку так, щоб трикутники зі зворотньої сторони, які мають одинакові номери опинились накладені один на одного. Починаємо з цифри 7, а потім – 6 і т. д.

Згинаючи гексагексафлексагон, можна побачити всі сім його поверхней. Якщо все виконано вірно, то на всіх трикутниках видимої сторони шестикутника повинна стояти цифра 1, а на всіх трикутниках на зворотній стороні – цифра 2.


2.5. Виготовлення гексагексафлексагона.
Інший, на менш цікавий флексагон отримав назву гексагексафлексагон ( перше «гекса» - шість- це значить кількість поверхней цієї моделі) .

1. Підготувати смужку паперу, розподілену на 19 рівносторонніх трикутників ( можна роздрукувати шаблон)
2. Зробити згини кожної лінії, які ділять смужку на трикутники в обидві сторони, щоб майбутній флексагон легко розкривався.
3. Прономерувати трикутники з однієї сторони цифрами
1,2,3,1,2,3,1,2,3,1,2,3,1,2,3,1,2,3.

Перевернути цю смужку і прономерувати трикутники на зворотній стороні цифрами 4,4,5,5,6,6,4,4,5,5,6,6,4,4,5,5,6,6.

Як варіант можна замість цифр розфарбувати в різні кольори ( кожній цифрі відповідає тільки один колір) чи намалювати на них будь-яку геометричну фігуру.
4. Скласти смужку так, щоб трикутники зі зворотної сторони, які мають одинакові номери опинились накладені один на одного. В результаті вийде ось така смужка.
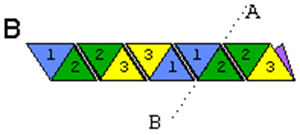
5. Зігнути по лінії аб, відігнувши 3 трикутники (3,2,2) вперед.
6. Зігнути по лінії сд, відігнувши з другої сторони 4 трикутники (1,1,3 і не прономерований) назад.
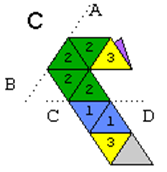
7. Залишається лише підігнути не прономерований трикутник вниз і приклеїти його до не прономерованого трикутника на нижній стороні смужки.
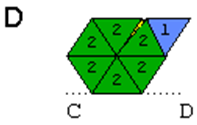
Згинаючи гексагексафлексагон, можна побачити всі шість його поверхней. Для цієї моделі сторони з цифрами 1, 2 і 3 будут з’являтися частіше, ніж 4, 5 і 6. Виконати всі дії значно легше ніж описати. Якщо все виконано вірно, то на всіх трикутниках видимої сторони шестикутника повинна стояти цифра 1, а на всіх трикутниках на зворотній стороні – цифра
2.
3. Шлях Таккермана
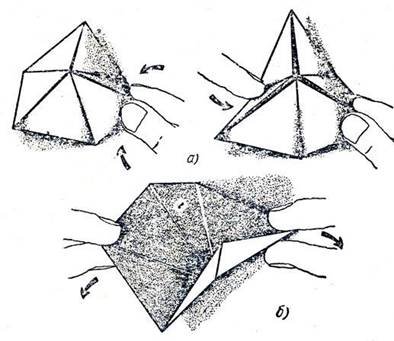
Щоб «відкрити» тригексагексафлексагон, потрібно одною рукою взяти за два сусідніх трикутники, прилеглих до будь-якої вершини шестикутника (а), а другою рукою потягнути за вільний край двох протилежних трикутників (б). Якщо флексагон не відкривається, потрібно спробувати взяти його за два інших трикутники. При розгортанні шестикутник вивертається навиворіт, і на ззовні виходить поверхня, яку раніше не було видно.
Маючи перед собою готові моделі шестикутників, потрібно перевірити як вони працюють. Якщо в моделях з 3-ма, 4-ма, 5-ма поверхнями відшукати кожну поверхню не дуже складно, то починаючи з гексагексафлексагону зявляються труднощі. Флексагон можна повертати до безкінечності, але побачити пяту і шосту і т.д. поверхні так і не вдавалось! Розібратись допоможе схема Таккермана для гексагексафлексагона. Їм був знайдений найпростіший спосіб виявлення всіх поверхней будь-якого флексагона: тримаючи флексагон за будь який кутик, слід відкривати фігуру до тих пір, поки вона «відкривається», а потім переходити до наступного кутика. Цей метод так і називається «шлях Таккермана». Він дозволяє побачити всі шість розворотів гексагексафлексагона за один цикл із 12 згинань. Поверхні з цифрами 1,2, і 3 будуть з’являтися в три рази частіше, ніж поверхні з цифрами 4,5 і 6. Шлях Таккермана зручно показати схематично. Стрілки показують, в якому порядку ставатимуть видимими поверхні флексагона. Схеми такого типу підходять для вивчення будь- якого різновиду флексагонів.
Повна математична теорія флексагонів була розроблена в 1940 році Тьюки і Фейманом. Крім цього теорія вказувала точний спосіб побудови флексагона.
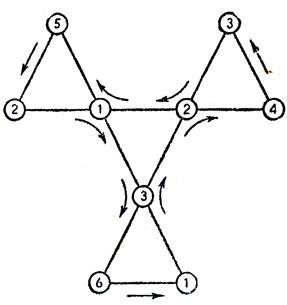
Схема 'шляху Таккермана' на гексагексафлексагоні
4. Виготовлення флексора
Кільця тетраедрів, що обертаються – це ланцюжок із тетраедрів володіє дивовижною здатністю згинатися і вивертатися до безкінечності, весь час міняючи форму. Кільце із тетраедрів – це перший приклад флексора – згинаного багатогранника.
Дж. М. Андреас і Р.М. Сталкер не залежно один від одного відкрили сімейство кінцевих багатогранників, що згинаються з 2n вершинами, 6n ребрами ( із яких 2n здвоєні) і 4n трикутними гранями; n може дорівнювати 6, 8, чи будь-якому більшому цілому числу. Гранями слугують грані n тетраедрів, з’єднаних між собою в циклічному порядку по визначених парах протилежних ребер кожного так, що виходить фігура схожа на кільце. При n = 6 ця фігура ще досить жорстка, але при n = 8 вона вже може згинатися і вивертатися до безкінечності. Якщо n парне число, фігура прийматиме симетричну форму.
Для виготовлення моделі флексора достатньо одного листка цупкого паперу.
4.1. Виготовлення шестикутного флексора
Кількість граней: 24
Кількість ребер: 30
Кількість вершин:12
|
|
|
|
Інструкція виготовлення флексорів |
|
|
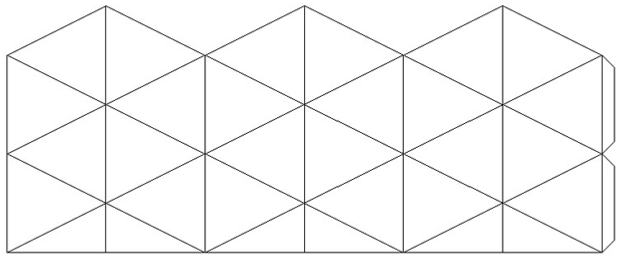
1. Розфарбувати шаблон, вирізати. |
|

2. Зробити лінії згину по вертикалі і діагоналі, добре загладити.

3. Вийде складена «трубка».

4. Склеїти (клеєм або двохстороннім скотчем).

5. Скласти модель в коло і склеїти.

6. Робота завершена.


4.2. восьмикутного флексора
32
40
Кількість вершин:16

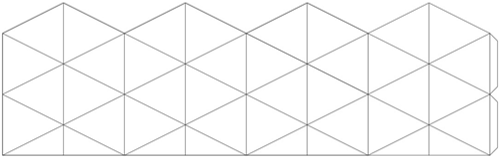
Шаблон восьмикутного флексора
|
Виготовляти восьмикутний флексор згідно попередньої інструкції ( дивитись інструкцію виготовлення флексорів) |
||
|
|
|
|
4.3. десятикутного флексора
40
50
Кількість вершин:20

Шаблон десятикутного флексора
Виготовляти десятикутний флексор згідно інструкції виготовлення флексорів.
4.4. дванадцятикутного флексора
48
60
Кількість вершин:24

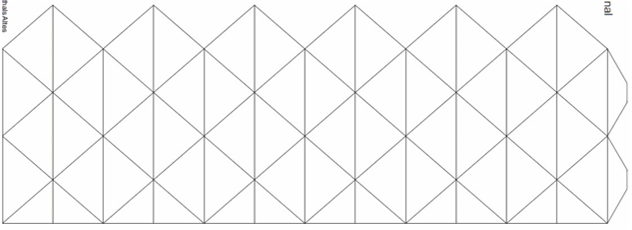
Шаблон дванадцятикутного флексора
Виготовляти дванадцятикутний флексор згідно інструкції виготовлення флексорів.


5. Суперечка про існування флексора
Кільце із тетраедрів як многогранник, що згинається викликає ряд суперечок.
По-перше, в ньому є отвір.
По-друге, є ребра до яких підходять по чотири грані. Так що не зрозуміло чи варто це кільце називати многогранником.
Щоб уникнути всяких сумнівів, при пошуку флексорів можна було б обмежитись тільки випуклими многогранниками, оскільки многогранники, лежать по одну сторону від кожної зі своїх граней. Але є знаменита теорема Коши про те, що будь-який многогранник незгинаючий. Вона була доведена в 1813 році. Хоча ця теорема не виключала існування не випуклих флексорів, але багато математиків вважали, що і таких флексорів теж не існує.
6. Магічне кільце із восьми тетраедрів.
Магічне кільце із восьми тетраедрів – є магічним в декількох сенсах. Математик Ройал В. Хит запропонував особливим чином розмістити в кожному трикутнику цього флексора числа от 1 до 32. Чотири грані кожного тетраедра дають в сумі 66; відповідні грані, взяті по одній із кожного тетраедра дають в сумі 132!
1) 1+16+25+24+2+15+26+23=132; 2) 28+22+3+13+27+21+4+14=132;


3) 7+9+32+18+8+10+31+17=132; 4) 30+19+6+11+29+20+5+12=132;


Крім цього, числа розміщені так, що чотири грані кожного тетраедра в сумі дають 66:
1) 1 + 30 + 7 + 28 = 66;
2) 12 + 17 + 14 + 23 = 66;
3) 31 + 4 + 26 + 5 = 66;
4) 21 + 15 + 20 + 10 = 66;
5) 2 + 29 + 8 + 27 = 66;
6) 11 + 18 + 13 + 24 = 66; 7) 32 + 3 + 25 + 6 = 66;
8) 22 + 16 + 19 + 9 = 66.
7. Корисні поради при виготовленні флексагонів та флексорів:
- Звичайний комп’ютерний папір полегшує складання флексорів, але така іграшка-головоломка не буде довго «служити». Для роботи краще використовувати папір щільністю 160г/м2 чи картон, лінії згину повинні бути добре «прогладжені», щоб флексор легко вивертався.
- Переконайтесь, що кожна лінія зігнута дуже добре. Використовуйте лінійку при згинанні ліній, щоб вони були чіткіші.
- Як варіант, можна замість цифр розфарбувати в різні кольори ( кожній цифрі відповідає тільки один колір).
- Молодшим дітям можна дозволити не звертати увагу на помітки в трикутниках, а просто розфарбовувати за бажанням.
- Використовуйте дуже густий клей ПВА чи інший хороший клей, і перш ніж повертати флексагон переконайтесь, що він висох. Адже місця склеювання будуть знаходитись в постійному русі і необхідно, щоб вони були надійно склеєні.
- Якщо помітили, що кінці флексагону все ж «вискакують», можна закріпити скотчем.
- Спочатку перевірте ваш флексагон, вивертаючи його повільно декілька разів. Це допоможе виявити не бажані складки і перевірити згини, в подальшому флексагон буде вивертатися легко і швидко.
8. Використання флексагонів і флексорів
На перший погляд, флексагони і їм подібні фігури (мають дивовижну властивість згинатись, показуючи нові грані) – всього лиш іграшки. Але вони зуміли привернути увагу в різних галузях. Ось декілька тому доказ: -шарнір подвійної дії, з’єднання якого є на всіх тетрафлексагонах, повсякденно використовується для петель дверей і вікон, в кріпленнях на настінні телевізори;
- флексагони пов’язані з багатьма математичними поняттями: стрічкою Мебіуса, Тором (тороідом). Крім цього цим «іграшкам» властиві чіткі правила математики, які вивчає наука флексологія;
- незвичний цикл згинання фігур привертає до них увагу, через це їх використовують в рекламних акціях. Крім цього до будь-якого флексагона можна прикріпити плоский предмет (те, на що виробники хочуть привернути увагу), і можна бути впевненим, що цим предметом зацікавляться (також використовують в маркетинзі).
- флексагони пов’язані з різними науками і речами: у формі флексагонів закручені молекули речовин (журнал «Химия и жизнь»), в стилі флексагонів створюються інтер’єри приміщень і предмети меблювання;
- велике застосування флексагони знайшли у дизайнерському мистецтві, тому що цикл перегинань цікавий при створенні меблів трансформерів, диванів, крісел, стільців та інше;
- і наостанок , флексагоноподібні фігури використовуються як вітальні листівки, іграшки. Вони слугують темами як наукових, так і не наукових дискусій, але до кінця їх таємниця не відкрита.





Висновок
Іграшки ніколи не були просто забавкою. Від самого початку існування людства вони виконували надзвичайно важливу роль – допомагали дитині вивчати оточуючий світ, а також готуватись до того, щоби стати самостійною людиною, яка здатна приймати самостійні рішення, керуючись власними знаннями та досвідом.
Із року в рік STEM-іграшки набувають все більшої популярності серед дітей та їхніх батьків. Причини цього очевидні: бавлячись з ними, дитина водночас розвивається та навчається. Флексагони і флексори – це не просто іграшка, це засіб математичного розвитку учнів. Розвивається просторова уява. Геометрія як планіметрія і стереометрія стають зрозумілими вже в початковій школі. Моделювання та створення флексагонів розвиває фантазію, творчість учня. За допомогою флексагонів можна вивчати цифри і букви, склад числа і таблицю множення. Узагальнювати і шукати невідповідності. Дуже корисні ці математичні іграшки в роботі з інклюзивними дітками – вони роблять процес навчання цікавішим і різноманітнішим.
Флексагони, як засіб математичного моделювання мають ряд переваг: економічність: для виготовлення флексагонів потрібні цупкий папір,
клей, ножиці, скотч, ольорові олівці та шаблон; доступність: при мінімальній допомозі дорослого дитина не тільки знаходить невидимі поверхні флексагону, але і моделює їх за шаблоном чи накресливши розгортку самостійно.
![]() розвиток: флексагони сприяють розвитку дрібної моторики, просторової уяви, пам’яті, уваги, терпіння та здатності розв’язувати проблеми, при спеціально продуманому оформленні активізує формування різних уявлень. Ігри на логіку також привчають дітей доводити розпочату справу до кінця.
розвиток: флексагони сприяють розвитку дрібної моторики, просторової уяви, пам’яті, уваги, терпіння та здатності розв’язувати проблеми, при спеціально продуманому оформленні активізує формування різних уявлень. Ігри на логіку також привчають дітей доводити розпочату справу до кінця.
Тому, такі паперові головоломки для дітей по праву вважається унікальним симбіозом математики і оригамі.
Література
1. Антоненко Е. Флексагоны. Ж. «Квантик». – М.: МЦНМО, 2012. № 4, С.14 – 18.
2. Гарднер М. Математические головоломки и развлечения. – М.: Мир, 1999. – 447 с.
3. Долбилин Н.П. Жесткость выпуклых многогранников. / Квант, №5, 1988. с.6-14.
4. Лиман М. М. Школьникам о математике и математиках. – М.:
Просвещение, 1981. – 80 с.
5. Кан И. Треугольные флексагоны. Ж. Наука и жизнь. – М.: Пресса,
1993.№ 12. – С. 42 – 43.
6. http://nsportal.ru/ap/library/khudozhestvenno-prikladnoe
7. tvorchestvo/2013/02/26/tvorcheskiy-proekt-fleksagony
8. http://gamejulia.ru/fleksagon-kak-sdelat-foto-i-video.html
9. http://www.openclass.ru/node/439535
Додатки
Шаблон тригексафлексагона
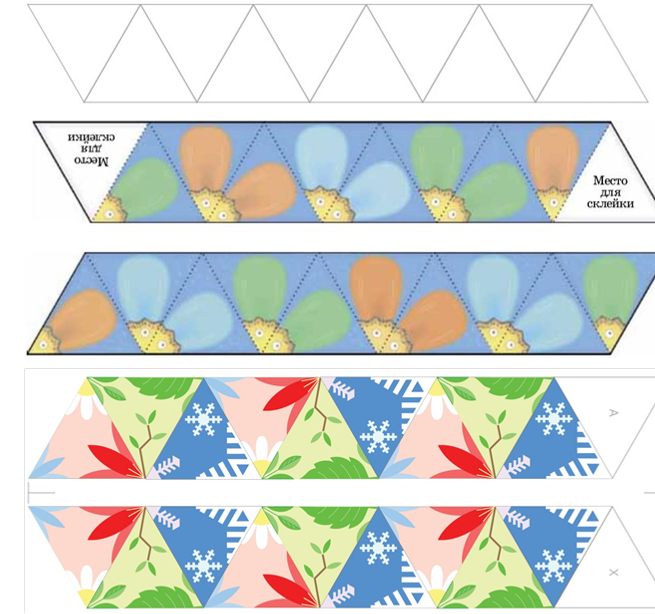
Шаблон тетрагексафлексагона
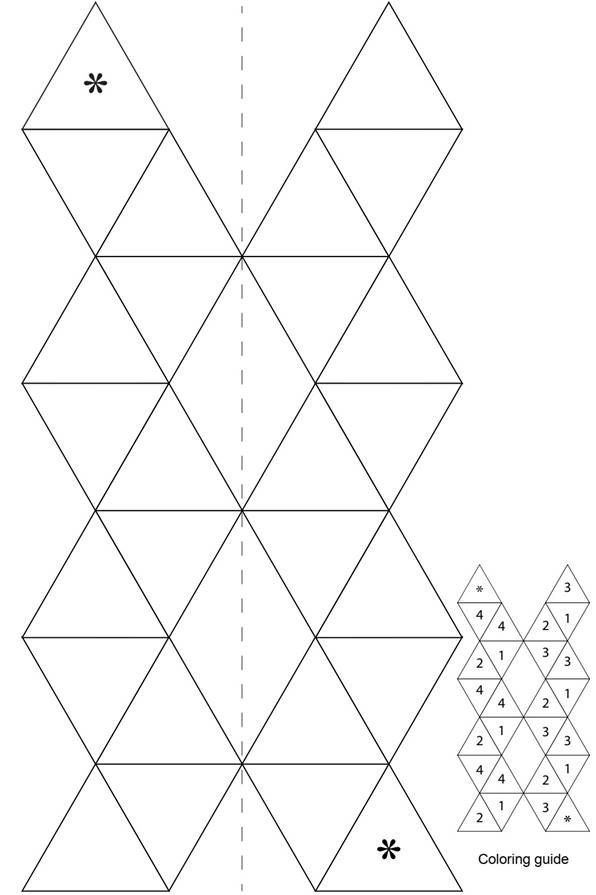
Шаблон пентагексафлексагона
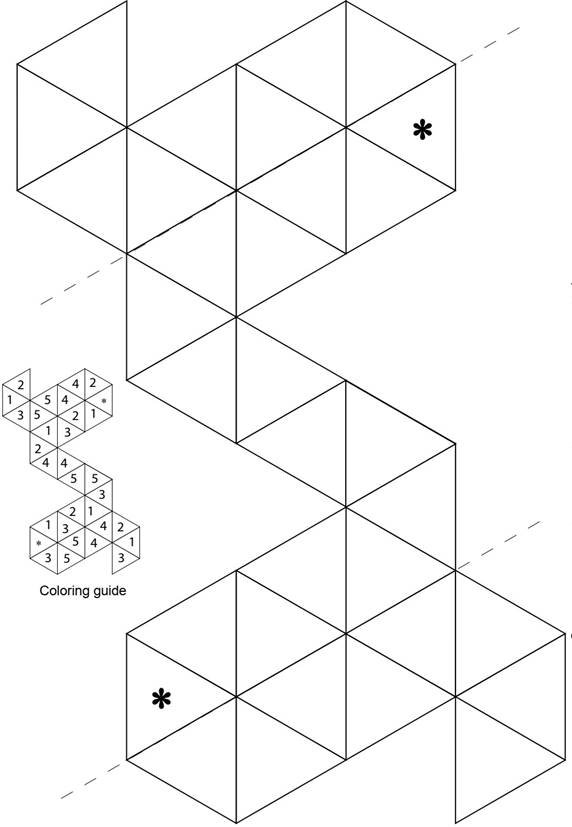
Шаблони шестикутного флексора

Шаблони восьмикутного флексора
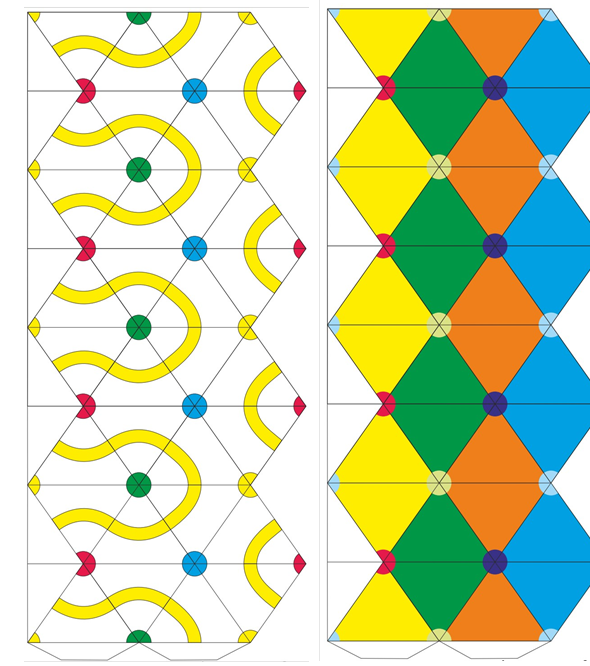
|
Шаблон десятикутного флексора |
Шаблон дванадцятикутного флексора |
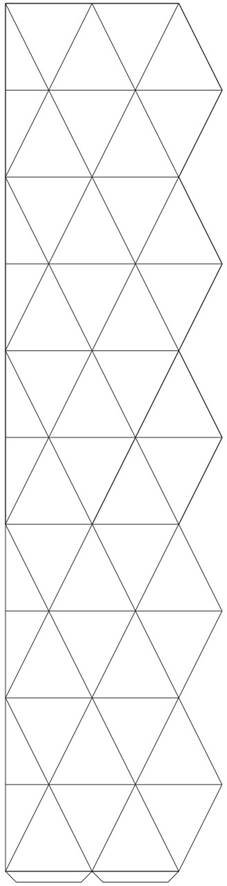
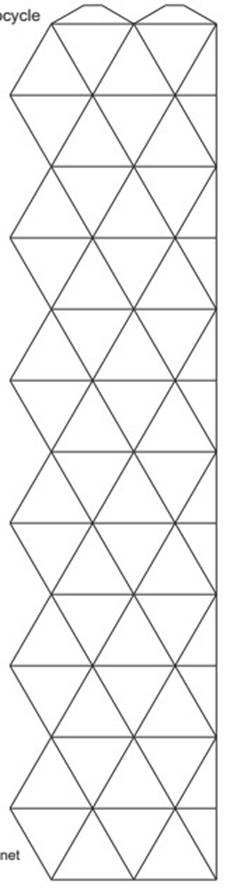
-
Дякую за вашу роботу
-


про публікацію авторської розробки
Додати розробку


