МІНІСТЕРСТВО СВІТИ І НАУКИ УКРАЇНИ 

ВІДДІЛ ОСВІТИ, МОЛОДІ ТА СПОРТУ НОВОУШИЦЬКОЇ  СЕЛИЩНОЇ РАДИ ПЕСЕЦЬКА ГІМНАЗІЯ

 

 

 

 

 

 

 

 

 

 

 

 

Сіваш Раїса Іванівна  учитель математики

Сіваш Валерій Вікторович учитель фізики та інформатики  

 

 

 

Сучасні уроки інтерактивного навчання  в математичній та природній галузях

(Інтегровані уроки)

 

Методичний посібник 

 

 

 

 

 

   

 

 

 

 

 

Песець 2022 р.

 

Автори:

 Сіваш Раїса Іванівна, вчитель математики Песецької гімназії Новоушицької селищної ради Хмельницької області.

 Сіваш Валерій Вікторович, вчитель фізики та інформатики Песецької гімназії Новоушицької селищної ради Хмельницької області.

 

 

 

 

 

Сіваш Р.І., Сіваш В.В. «Сучасні уроки інтерактивного навчання в математичній та природничій галузях». 

Методичний посібник. Песець, 2022. 35c.

 

 

 

 

 

 

 

 

Рецензенти: Савлюк Н.І., Космак Л.В. 

Схвалено: методичною радою Песецької гімназії від 21.02.2022 року № 4.

 

 

 

 

 

 

 

 

 

 

 

 

В даному посібнику запропоновано методичні розробки сучасних інтегрованих уроків фізики та математики, з метою формування в учнів кращих знань з даних предметів, вміння застосовувати ці знання на практиці. Такі уроки підвищують мотивацію навчання, розвивають навички самоосвіти, аналітичні здібності , удосконалюють комунікативно-пізнавальні вміння. Учні на таких уроках обмінюються знаннями в умовах співробітництва. Автори сподіваються, що він стане в нагоді іншим учителям під час підготовки до уроків.

 

            

ЗМІСТ

Вступ……………………………………………………………………………...…4

1.   Методи навчання……...…………………………………………...…………….6

1.1.   Нестандартні методи …………………………………………………...7 1.2. Типи сучасних уроків ………………………………………………..…8

2.   Розробки інтерактивних уроків:

2.1.   ІНТЕГРОВАНИЙ УРОК ФІЗИКИ ТА МАТЕМАТИКИ

Тема: " Графічне зображення рівномірного руху" ……………………..…9

2.2.   ІНТЕРАКТИВНИЙ УРОК  ФІЗИКИ ТА МАТЕМАТИКИ

Тема. «Рівноприскорений прямолінійний рух. Прискорення. Швидкість.

Пряма пропорційність величин.»  ………………………………………....18

2.3.   ІНТЕГРОВАНИЙ  УРОК ФІЗИКИ ТА МАТЕМАТИКИ

Тема. Переміщення під час прямолінійного рівноприскореного руху.

Рівняння координати. Площа трапеції. Квадратична функція………….…24

2.4.   ІНТЕГРОВАНОГО УРОКУ З МАТЕМАТИКИ І ФІЗИКИ

( групові форми роботи, інтерактивна технологія «Ажурна пилка») ………….29

Висновки……………………………………………………………………………34

Література…………………………………………………………………………..35 ВСТУП

«Наука – починається там, де починають, щось вимірювати» Д.І. Менделєєв.

Сучасний урок – це урок демократичний. Він проводиться не для учнів, а разом з нами. Його характеризує не навчання словом, а навчання справою. У  підготовці до уроку виділяють три етапи:

ØДіагностичний, що передбачає вивчення особливостей та інтересів учнів, їх  рівня  підготовки до уроку, аналіз навчального матеріалу.

ØПрогнозування, який включає вибір  найбільш оптимальної стратегії навчання  учнів і оцінку різних варіантів проведення уроків у контексті  обраної стратегії.

ØПланування, що має на меті створення  плану та програми управління  навчальною діяльністю учнів.

Інтерактивний  урок являє собою нестандартну форму навчання з реалізації між предметних зв’язків і є практичним відображенням інтегральної технології навчання. Як правило, бінарний урок являється творчістю двох педагогів. Але в окремих випадках такий урок може проводити і один учитель, якщо він в одному і тому ж класі викладає два різні предмети, наприклад,  математику і фізику. Такі уроки переростають у творчий процес учнів і формують в них креативну компетентність.

Інтерактивні уроки мають значні переваги над традиційними уроками.  Вони розширюють кругозір, поглиблюють уявлення про предмет, сприяють формуванню інтелектуально розвиненої особистості. Такі уроки розвивають вміння порівнювати, робити висновки, розвивати математичне мовлення (якщо це поєднання математики з будь-яким іншим шкільним предметом).

 Інтегровані уроки є джерелом знаходження зв’язків між різними шкільними предметами, вивченням явищ з декількох сторін. Тому у формі інтегрованих уроків доцільно вивчати нові теми, користуючись законами чи дослідженнями в інших шкільних предметах. Адже інтегрований урок вирішує не окремі завдання, а їх сукупність. Такі уроки концентрують увагу учнів і стимулюють їх пізнавальну діяльність. 

При підготовці до інтегрованого уроку учителі (чи учитель) мають проявити творчий підхід, піднести матеріал так, щоб учням було зрозуміло і цікаво. Урок має бути чітким, продуманим на всіх етапах. Бажано залучати учнів до підготовки такого уроку. 

Такі уроки благотворно впливають на активність головного мозку, знижують його втомлюваність, підвищують успішність навчання. 

Інтегрований урок має такі ознаки:

1.     Спеціально організований, підготовлений;

2.     Має специфічну мету, наприклад:

А) більш глибоко проникнути в суть теми,  яку вивчають;

Б) підвищити інтерес учнів до предметів;

В) цілісного сприйняття досліджуваних з даної теми питань;

Г) економії навчального часу і т. п.;

3.     Поглиблене здійснення між предметних зв’язків;

4.     Синтезування знань;

5.     Заглибленість вивчення;

6.     Практична значущість і актуальність мети проведення, що вчить зіставляти теорію з практикою, розвиває критичність мислення.

Сучасні інтегровані уроки будуть ефективними при умові дотримання таких педагогічних умов:

●        правильного виділення між предметних об’єктів за допомогою аналізу навчальних програм;

●        раціонально організованої спільної роботи вчителів із підготовки уроку (взаємне консультування, складання спільного плану уроку, визначення глибини та об’єму розкриття навчального матеріалу, вибір методів та засобів навчання);

●        бажано, щоб учитель займав не більше половини часу уроку, решта повинно припадати на учнів;

●        активізація пізнавальної діяльності школярів на всіх етапах уроку;

●        урізноманітнення форм навчальної роботи та забезпечення наступності між ними.

Мета сучасного  уроку – основа ефективної діяльності не тільки вчителя, а й учнів. Вона визначає  характер їх взаємодії, реалізується не тільки в їх діяльності, а й діяльності учнів, і досягається тільки в тому випадку, коли до цього прагнуть обидві сторони.  Тому мета уроку має ставитися перед класом в учнівському варіанті та доводиться  до рівня розуміння та прийняття школярами.

Триєдина мета уроку може мати занадто загальний характер. Її обов’язково необхідно конкретизувати за цілями етапів і навчально-виховних моментів уроку.

Проблема інтеграції фізики і математики є надзвичайно важливою, адже математична підготовка школярів певною мірою впливає на рівень знань із фізики. Існує думка, що міжпредметний зв'язок „фізика-математика” ґрунтується на основі загальних фізико-математичних понять (функція, відношення, змінна, величина, залежність, вектор, геометричні перетворення тощо). Зокрема, математичні моделі ефективно „працюють” при розв’язуванні фізичних задач, без яких не може бути реалізоване надійне засвоєння й розуміння фізики. Саме тому інтеграція фізики і математики сприяє кращому засвоєнню і розумінню учнями обох предметів. Поданий інтегрований урок (фізика + математика)  рекомендовано для використання на уроці фізики в 7 класі за темою «Графічне зображення руху». За програмою з алгебри учні 7 класу тему «Графіки лінійних функцій» вивчають в ІІ семестрі, а за програмою з фізики тема «Графічне зображення руху» вивчається в жовтні. (З цією проблемою стикалися всі вчителі фізики). Учитель математики на прохання колеги-фізика поміняла місцями теми «Функція» та «Лінійні рівняння», що не змінило основних завдань вивчення курсу алгебри в 7 класі, але дало можливість перед вивченням теми з фізики, дати учням необхідні знання про графіки лінійних функцій. Ці знання, які активізує на уроці вчитель математики, сприяють кращому розумінню та засвоєнню учнями теми з фізики. 

1. МЕТОДИ НАВЧАННЯ

Способи навчання, які використовуються вчителем і учнями в їх сумісній і  взаємопов’язаній роботі, спрямованій  на досягнення цілей навчання,  називають методами навчання. Кожний метод навчання може бути  описаний і розкритий через різноманітність  прийомів, що використовуються під час його реалізації.. Прийом навчання – складова  частина методу.

Пояснювально-ілюстораний метод навчання полягає в тому,  що вчитель передає учням готову інформацію за допомогою різних засобів навчання, а учні сприймають, осмислюють і фіксують її пам’ять.

Репродуктивний метод навчання використовується для формування  вмінь і навичок учнів на рівні, що дозволяє застосувати  їх в умовах, які раніше  розглядалися, або трохи змінених. Учитель за допомогою  системи завдань  організовує діяльність учнів з неодноразового відтворення повідомлених знань або способів  діяльності.

Метод проблемного  викладу навчального матеріалу полягає в тому, що вчитель не тільки організовує передачу інформації різними способами, а і знайомить учнів із процесом пошуку розв’язання тієї чи іншої проблеми.

Евристичний (частково-пошуковий)  метод – це метод, при якому вчитель організовує участь учнів у виконанні окремих кроків пошуку розв’язання  проблеми. Роль учителя полягає в конструюванні пізнавального завдання,  розчленуванні його на окремі етапи,  визначенні  тих етапів, які  учні виконуватимуть самостійно, тобто вчитель  організовує самостійно-пізнавальну діяльність учнів. В одних умовах учнів участь бачити проблему в іншихбудувати докази, у третіх – робити  висновки з викладених або продемонстрованих фактів, у четвертих – висловлювати гіпотези, у п’ятих – складати план перевірки висловлюваних припущень та інше. Тобто організовується засвоєння досвіду творчої діяльності за елементами оволодіння окремими етапами розв’язання проблемних   задач.

 Сутність дослідницького методу полягає в організації  вчителем пошукової, творчої діяльності учнів з розв’язання нових проблем і проблемних ситуацій. Назва цього методу передбачає  досконале засвоєння учнями досвіду творчої  діяльності. Дослідження психологів показали, що участь учнів у частковому вирішенні  творчих проблем не приводить до формування вмінь досліджувати й аналізувати цілісні задачі.

 

Раціональне застосування методів  навчання

Методи навчання	При якому змісті матеріалу доцільно застосовувати?	При розв’язанні яких задач ефективні?	До яких учнів дають найкращий результат?	Які можливості повинен мати вчитель?
Словесні	Матеріал теоретикоінформаційного змісту	Формування знань теоретичного та практичного характеру	Готових до сприймання вербальної інформації	Такі, якими володіє краще, ніж іншими
Наочні	Такому, що може бути поданий у наочному вигляді	Розвиток уваги, спостережливості, уміння аналізувати	Для учнів із чуттєво-образним мисленням	Може знайти та самостійно виготовити наочність
Практичні	Коли зміст має прикладний характер	Розвиток практичних умінь і навичок, збагачення досвіду	Готових до виконання практичних завдань	Наявність приладів, посібників для учнів
Репродукти вні	Занадто простий чи дуже складний	Формування  базових знань, умінь і навичок	Не готових до проблемного навчання	Не має часу на застосування інших методів.
Проблемнопошукові	Зміст середнього рівня складності	Розвиток мислення, дослідницьких умінь, творчого підходу до справи	Тих, які володіють необхідними  вміннями	Володіє методикою проблемного навчання, має час
Індуктивні	Зміст викладений за індуктивною логікою	Розвиток умінь узагальнювати, мислити від конкретного до загального	Таких, які утруднюються в дедуктивних міркуваннях	Учитель  володіє індуктивними методами
Дедуктивні	Зміст раціонально викладати в такий спосіб	Розвиток мислення  (від загального до конкретного)	Учні мають відповідний розвиток мислення	Учитель володіє дедуктивними методами
Самостійна робота	Зміст доступний для самостійного вивчення	Формування навичок навчальної праці	Учні мають відповідний рівень знань, умінь, навичок.	Є дидактичні матеріали для кожного учня, учитель уміє керувати роботою дітей
Продуктивн і	Зміст, сприятливий для засвоєння його шляхом відкриття нового знання	Розвиток умінь продукувати нове знання	Учні готові  до самостійної творчої діяльності	Учитель володіє методикою організації продуктивної діяльності

 

1.1. НЕСТАНДАРТНІ МЕТОДИ

 Метод складної цілі, який дозволяє планувати навчання учнів у зоні їх найближчого розвитку та забезпечує формування  відповідальності, переконання в можливості подолання труднощів, що виникають на життєвому шляху, віру у  свої сили.

 Метод вибору, котрий дозволяє створити умови для прийняття учнями  навчальної задачі, захоплення пізнавальною діяльністю, в якій вони можуть  почуватися особистостями.

 Метод випередження, який сприяє прискореному розвитку сильних учнів  класу, дає можливість слабким усвідомити найбільш важкі місця навчальної  програми.

 Метод укрупнення  блоків, який допомагає засвоїти головні, істотні поняття розділу, зв’язки між ними, зменшити навантаження  на учнів.

 Метод самоаналізу та колективної творчості, характерною рисою якого є  залучення учнів до групових форм діяльності з метою створення нового продукту  та активне використання рефлексії.

 Метод індивідуалізованого застосування програм залежно від особливостей учня, який дозволяє створювати для кожного школяра траєкторію  індивідуального вивчення теми.

1.2. ТИПИ СУЧАСНИХ УРОКІВ

 Традиційним типологія уроків проводиться на підставі складу їх структурних компонентів. За цих умов окреслюють такі типи уроків: вступний, урок вивчення нового матеріалу, урок закріплення знань і формування умінь і навичок, повторювально-узагальнюючий, контрольно-перевіряючий.

 За провідним методом виділяють: урок лекцію, урок диспут, ігровий урок, урок-подорож та ін.  За дидактичним задумом (підходом) поряд із традиційними видами уроків (комбінований, інформаційний)  виділяють інтегрований урок, проблемний урок та ін. 

 Сьогодні найбільш поширена є типологія уроків за ціллю, що  переважає. Так, за когнітивними цілями виділяють: 1-й – урок засвоєння нових знань; 2-й – урок  формування вмінь і навичок; 3-й – урок застосування знань;  4-й – урок узагальнення та систематизації знань; 5-й – урок контролю й оцінювання навчальних досягнень; 6-й – комбінований урок.

 Усе більша кількість учених схиляється до думки про доцільність створення  циклів уроків, проведення яких спряло б залученню учнів до тих видів діяльності, у процесі яких досягаються намічені цілі. Циклом називають певну послідовність уроків, об’єднаних  за будь-яким критерієм, яка може повторюватись. Так, за І.Підласним , цикл може включати;

-         вступний урок;

-         уроки засвоєння нових знань;

-         уроки розвитку нових умінь, навичок;

-         уроки узагальнення, систематизації; - уроки контролю та корекції знань і вмінь; - підсумковий урок.

    

2. РОЗРОБКИ ІНТЕГРОВАНИХ УРОКІВ

2.1. ІНТЕГРОВАНИЙ УРОК ФІЗИКИ ТА МАТЕМАТИКИ

Тема: " Графічне зображення рівномірного руху"

Мета: Навчальна. Ввести поняття прямолінійного рівномірного руху; використовувати знання, отримані на уроках математики, для побудови графіків рівномірного руху ,для визначення за графіками пройденого тілом шляху, швидкості, часу руху; домогтися розуміння функціональної залежності між величинами. 

Розвиваюча. Розвивати навички читання графіків, логічне мислення, вміння аналізувати, порівнювати, працювати з інформацією; шукати зв’язки між предметами, застосовувати отримані знання на практиці.

 Виховна. Виховувати культуру оформлення розв’язків до графічних задач та культуру мовлення; виховувати творчу особистість учнів.

Тип уроку: вивчення нових знань – ІНТЕГРОВАНИЙ УРОК (фізика і математика)

Обладнання: інструкції до уроку, диференційовані на три рівні, мультимедійна установка.

Хід уроку

1.     Організаційний етап

2.     Мотивація

3.     Актуалізація знань

Вчитель фізики.

І. «Глибоке занурення в фізику» - фронтальне опитування:

1 питання – 0,5 бал.

1.Що називається механічним рухом?

2.   Що називається траєкторією?

3.   На які види поділяють механічний рух за формою траєкторії?

4.   Що називається шляхом?

5.В яких одиницях вимірюється шлях в системі СІ?

6.Яка фізична величина є характеристикою механічного руху?

7.   В яких одиницях в системі СІ вимірюють швидкість?

8.   Формула для обчислення швидкості?

9.Формула для обчислення шляху?

10. Який рух називають прямолінійний рівномірний?

ІІ. Перевірка домашнього завдання.

Вправа  9 (2,5). Відповіді: 2 зав. – 960 м., 5 зав. - третій рухався швидше, найбільшу відстань подолав другий, найдовше рухався другий.

Вчитель: Діти, ви знаєте, задачі в фізиці можна розв’язувати двома способами. Той, яким ви розв’язували вдома і ми в класі називають аналітичний спосіб. А є ще й другий – графічний. Не всі фізичні задачі можна вирішити цим способом, але деякі мають лише один спосіб вирішення – графічний. Та мабуть зрозуміло, для того, щоб користуватися цим способом нам спочатку треба навчитися описувати фізичні процеси за допомогою графіків. І почнемо ми з графіків рівномірного руху.

Отже, тема уроку «Графічне зображення рівномірного руху».

Як завжди хочу звернутися до ваших знань: які слова, терміни вам знайомі? Дійсно, ви вивчали графіки на уроках математики.

Тому цей урок ми проведемо разом з вчителем математики. Я переконана вона нам дуже допоможе навчитися будувати і читати графіки рівномірного руху.

Та перед тим, як надати слово вчителю математики, хочу зачитати вам слова великого вченого 

Галілео Галілея: «Якщо хтось досягне успіху у пізнанні природи і природа заговорить з ним, то заговорить вона мовою математики».

Вчитель математики.  Дійсно, важко переоцінити роль математики у вивченні інших предметів, у розвитку інших наук. А між фізикою і математикою існує тісний зв'язок. Математичні моделі широко використовуються під час розв’язання фізичних задач. І сьогодні ви самі в цьому переконаєтеся. Тож давайте згадаємо:

Слайд 3     

                                                  Слайд 4                                                            Слайд 6  

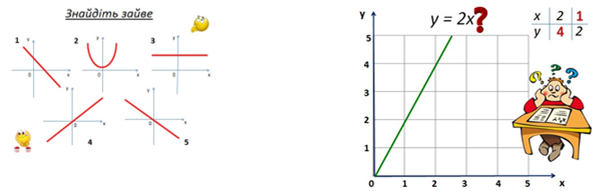
Слайд 5    

Слайд 7  

                                               

Я надіюсь, що згаданий нами матеріал скоротить час на вивчення нової теми з фізики та полегшить її розуміння. 

Вчитель фізики. Отже, починаємо. Щоб збільшити ККД нашого уроку, пропоную вам користуватися інструкціями до уроку. 

Прочитаємо завдання № 1:

Сучасний український літак АН – 158, рухаючись рівномірно, подолав 400 км за 30 хв. Побудуйте графік залежності шляху, що подолав літак, від часу – графік шляху.

Дайте відповідь на питання, що потрібно знати, щоб побудувати графік?

(Рівняння руху). А для того, щоб його записати, що треба знайти? (Швидкість).

Отже, розв’язуємо задачу: знаходимо швидкість руху, записуємо рівняння руху, визначаємо координати 2-х точок, будуємо графік шляху.

Робимо висновок № 1. 

Питання:  чи можу я за графіком визначити, який шлях пролетить літак за 2 год.

А зараз згадаємо літо… Ми – пливемо…. А назустріч – чемпіон по плаванню серед тварин – кальмар. Він здійснює реактивний рух, тому розвинув швидкість 200 км/год. Давайте на цій же координатній площині побудуємо графік шляху кальмара. 

 

 

Робимо висновок № 2. 

Слайд на екрані – графік шляху тіла (для груп А, В). 

Група С виконує завдання на 72 стор. впр.10 рис.2 – яке тіло рухається з найбільшою швидкістю?

 

                                                                                0                       10                    20                     30       t, c  

Питання: 

1.     Як рухалось тіло?

2.     Який шлях воно подолало за перші 10 с? 3. Якою була швидкість на кожній ділянці?

 

Отже, що  ми можемо дізнатися за графіками шляху:

1.   Характер руху

2.   Визначати шлях за будь-який час.

3.   Визначати швидкість.

4.   Порівнювати швидкості різних тіл.

 

 

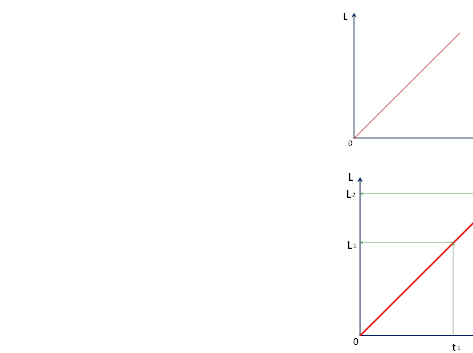
А зараз ми знову повернемося до першої задачі. Наше наступне завдання побудувати графік швидкості рівномірного руху. Вже по аналогії ми запишемо рівняння. Яким воно буде. V=800 км/год, V=200 км/год. Чи є в кого пропозиції.

Заслухати учнів.

Побудувати V(t).

Який можна зробити висновок. Що можна дізнатися за графіком швидкості?

1. Характер руху.

2.Порівнювати швидкості різних тіл.

3. Знаходити шлях.

І останнє завдання. № 6.36. Підказка – уважно роздивитися масштаб.

Вчитель фізики. Чи можна сказати, що ми виконали завдання уроку? А от про вчителя математики забули. Надаємо їй слово.

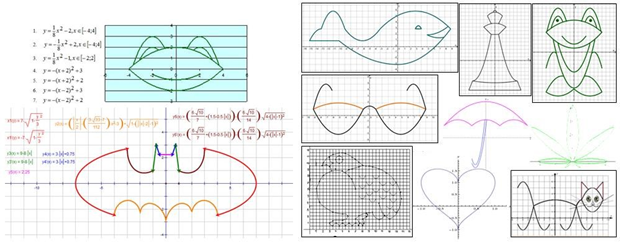
Вчитель математики: демонструє на слайдах та розповідає, в яких галузях нашого життя людина використовує графіки та графічну інформацію.

 

З графіками ми зустрічаємося не тільки на уроках у школі (слайд 1). Якщо придивитися, то можна побачити, що вони оточують нас і у повсякденному житті: в природі – веселка, береги річки, дороги, гори, траєкторія польоту комети мають форму графіків функцій (слайд 2),  в будівництві – це залізничні колії, лінії електропередач, сходи, мости, американські гірки (слайд 3)

 

У медицині (слайд 4) лікарі за допомогою графіків описують роботу серця та головного мозку.

 

У статистиці їх використовують для наочного відображення динаміки процесів та явищ (слайд 5).

Синоптики будують графіки для спостережень та прогнозування змін у природі (слайд 6).

Графіки використовують також у мистецтві (слайд 7).

Нотний стан складається із графіків функцій.

За допомогою графіків можна малювати картини. Так, ілюстрації до роману Пушкіна «Євгеній Онєгін» виконані художником Миколою Васильовичем Кузьміним за допомогою графіків різних функцій.

 

Будуючи за точками графіки функцій у координатній площині, ми також можемо створювати різні цікаві зображення (слайд 8, слайд 9).

 

 

Вчитель фізики: Оцініть свою корисну дію на уроці по 7-ми бальній шкалі, та визначте загальний бал за урок, додавши бали за теоретичну розминку.

Підсумок уроку. 

Домашнє завдання – переписати з інструкцій.

                                                      ІНСТРУКЦІЯ                                        

до уроку за темою: «Графічне зображення рівномірного руху».

І. Питання: знаєш відповідь – 0,5 бал.

1.                                                                                                                                                                                 7.

2.                                                                                                                                                                                 8.

3.                                                                                                                                                                                 9.

4.                                                                                                                                                                                 10.

5.                                                                                                                                                                                 Всього ___________

6.

ІІ. Задача: Сучасний український літак АН – 158, рухаючись рівномірно, подолав 400 км за 30 хв. Побудуйте графік залежності шляху, що подолав літак, від часу (графік шляху) – l(t).

ІІІ. Завдання: «Чемпіон з плавання» серед тварин  кальмар розвинув швидкість 200 км/год. Побудувати графік залежності шляху від часу.

Підказка:  щоб побудувати графік залежності шляху від часу, спочатку треба записати рівняння залежності шляху від часу. 

ІУ. Завдання:

Питання до графіка руху тіла:

1.   Як рухалось тіло?

2.   Який шлях воно подолало за перші 10 с?

3.   Якою була швидкість на кожній ділянці?

ЩО МОЖНА ДІЗНАТИСЯ ЗА ГРАФІКОМ ШЛЯХУ?

У. Завдання: за умовою задачі будуємо графіки швидкості літака та кальмара.

Підказка: якщо швидкість з часом не змінюється, то яке буде рівняння швидкості?

УІ. Завдання: розв’яжемо (усно) задачу № 6.38

ЩО МОЖНА ДІЗНАТИСЯ ЗА ГРАФІКАМИ ШВИДКОСТІ?

Корисна дія на уроці (0-7б.) _________ + бали за питання ______ = _______

Домашнє завдання: параграф 10, № 6.37, 6.41, впр.10(4) *

             

ІНСТРУКЦІЯ

до уроку за темою: «Графічне зображення рівномірного руху». І. Питання: знаєш відповідь – 0,5 бал.

1.                                                                                                                                                                                  7.

2.                                                                                                                                                                                  8.

3.                                                                                                                                                                                  9.

4.                                                                                                                                                                                  10.

5.                                                                                                                                                                                  Всього __________

6.

ІІ. Задача: Сучасний український літак АН – 158, рухаючись рівномірно, подолав 400 км за 30 хв. Побудуйте графік залежності шляху, що подолав літак, від часу (графік шляху) – l(t).

ІІІ. Завдання: «Чемпіон з плавання» серед тварин  кальмар розвинув швидкість 200 км/год. Побудувати графік залежності шляху від часу.

Підказка:  щоб побудувати графік залежності шляху від часу, спочатку треба записати рівняння залежності шляху від часу:   l=v·t

Складіть табличку (як в попередній задачі) для знаходження координат двох точок, але одна з яких буде  – (0; 0). 

ІV. Завдання:

Питання до графіка руху тіла:

1.   Як рухалось тіло?

2.   Який шлях воно подолало за перші 10 с?

3.   Якою була швидкість на кожній ділянці?

ЩО МОЖНА ДІЗНАТИСЯ ЗА ГРАФІКОМ ШЛЯХУ?

Підказка: ст.69 2 частина - 4)

V. Завдання: за умовою задачі будуємо графіки швидкості літака та кальмара.

Підказка: якщо швидкість з часом не змінюється, то яке буде рівняння швидкості?

VІ. Завдання: розв’яжемо (усно) задачу № 6.38

ЩО МОЖНА ДІЗНАТИСЯ ЗА ГРАФІКАМИ ШВИДКОСТІ?

Підказка: ст..71 «Підбиваємо підсумки».

Корисна дія на уроці (0-7б.) _________ + бали за питання ______ = _______ Домашнє завдання: параграф 10, № 6.37, 6.41.

ІНСТРУКЦІЯ

до уроку за темою: «Графічне зображення рівномірного руху». І. Питання: знаєш відповідь – 0,5 бал.

                1.                                                                                                                       7.

2.

8.

3.

9.

4.

5.                                                                                                                                                                                  10.

6.                                                                                                                                                                                  Всього ___________

ІІ. Задача: Сучасний український літак АН – 158, рухаючись рівномірно, подолав 400 км за 30 хв. Побудуйте графік залежності шляху, що подолав літак, від часу (графік шляху) – l(t).

ІІІ. Завдання: «Чемпіон з плавання» серед тварин  кальмар розвинув швидкість 200 км/год. Побудувати графік залежності шляху від часу.

Підказка:  щоб побудувати графік залежності шляху від часу, спочатку треба записати рівняння залежності шляху від часу:   l=v·t

Складіть табличку (як в попередній задачі) для знаходження координат двох точок,  одна з яких буде  – (0; 0). 

ІV. Завдання: на стор. 72 підручника розгляньте малюнок 2. Запишіть в зошит – яке з 3-х тіл рухається з більшою швидкістю. Підказка: стор. 69 - рис. 10.4.

ЩО МОЖНА ДІЗНАТИСЯ ЗА ГРАФІКОМ ШЛЯХУ?

Підказка: ст.69 2 частина - 4)

V. Завдання: за умовою задачі будуємо графіки швидкості літака та кальмара.

Підказка: якщо швидкість з часом не змінюється, то яке буде рівняння швидкості буде наступне: v = 200.

VІ. Завдання: розв’яжемо (усно) задачу № 6.38

ЩО МОЖНА ДІЗНАТИСЯ ЗА ГРАФІКАМИ ШВИДКОСТІ?

Підказка: ст.71 «Підбиваємо підсумки» - прочитати все!

Корисна дія на уроці (0-7б.) _________ + бали за питання ______ = _______

Домашнє завдання: параграф 10, № 6.37, 6.41.

 

             

2.2. ІНТЕРАКТИВНИЙ УРОК  ФІЗИКИ ТА МАТЕМАТИКИ Тема. Рівноприскорений прямолінійний рух. Прискорення. Швидкість. Пряма пропорційність величин. Мета: 

-         формувати знання про рівноприскорений прямолінійний рух і фізичні величини, що його описують, - прискорення та швидкість;

-         формувати вміння застосовувати раніше отримані знання при розв’язувані типових задач в курсі алгебри і фізики;

-         повторити, узагальнити і застосувати знання прямої пропорційності величин при розв’язуванні якісних, розрахункових і експериментальних задач з фізики із застосуванням ІКТ;

-         розвивати пізнавальну активність і творчі здібності учнів.

Наочність і обладнання: металевий жолоб, кулька, секундомір, штатив, пристрій для демонстрації слайдів.

                                              Хід уроку

I.                  Організаційний момент.

II.               Оголошення теми і мети уроку.

Учитель фізики

Галілео Галілей казав: «Математика – це мова, на якій написана книга природи», а так як фізика – наука про природу, то неможливо вивчати закони природи без теоретичних основ математики. 

Сьогодні на уроці ви ознайомитесь з рівноприскореним рухом, але на початку повторимо поняття прямої пропорційності величин.

III.           Учитель математики        

Загальний вигляд лінійної функції у=kx+b. Область визначення – множина дійсних чисел (D(у)=R).

 Це аналітичний спосіб задання. Ще можна задати функцію графічно і табличкою (можливо учні самі будуть відповідати на питання учителя щодо способів задання функції)

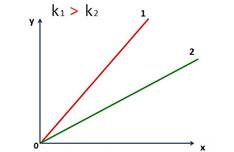
Графіком цієї функції являється пряма лінія. Якщо k>0, то, як ми бачимо, пряма перетинає вісь ОХ під гострим кутом відносно додатного напрямку осі.   Якщо k<0, то пряма перетинає вісь ОХ під тупим кутом відносно додатного напрямку осі.   

Слайд 1

 

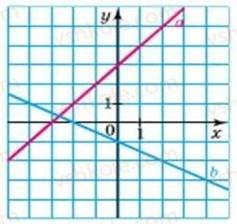
Лінійна функція

y=kx + b

область визначення – дійсні числа графік – пряма.

Якщо k=0, то лінійна функція матиме вигляд: у = kx. ЇЇ особливість в тому, що пряма перетинає початок координат. Цю функцію називають пряма пропорційність.

Слайд 2

 

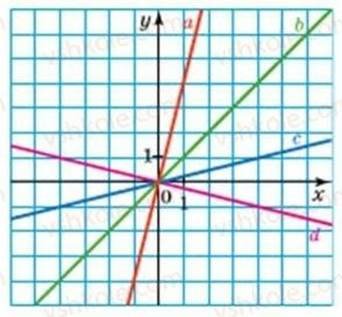
Пряма пропорційність y=kx

IV.            А) Виконайте перше завдання на картці контролю засвоєння знань.

№1

Із запропонованих графіків виберіть графіки лінійних функцій та прямої пропорційності.

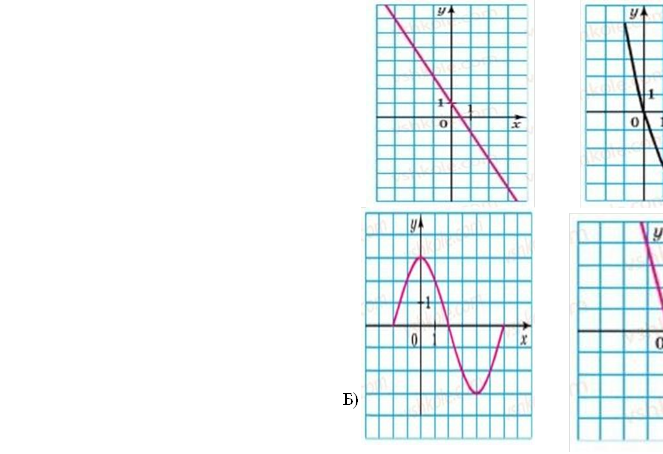
Пішохід рухається рівномірно з пункту А в пункт В зі швидкістю 5км/год. Задайте формулою залежність шляху S, пройденого пішоходом від часу t. Відповідь: S=5t 

V.               Учитель фізики

Коли пішохід рухається, то положення його тіла змінюється в просторі з часом відносно інших тіл. Такий рух називається механічним. 

(аналізуємо слайд 4, учні записують означення механічного руху в зошити)

  Слайд 4

У даній задачі автомобіль вважають           матеріальною точкою. Праворуч блакитного автомобіля знаходиться світлофор, а ліворуч – пішохід.

Проїхавши перехрестя, праворуч буде інший пішохід, а ліворуч – мотоцикліст. Отже, блакитний автомобіль змінив своє положення в просторі з часом відносно інших тіл.

         

Учитель математики

Слайд 5

 

Якщо напрямок вектора збігається з напрямком осі координат, то проекція на вісь ОХ дорівнює модулю вектора. Якщо напрямок вектора протилежний до  напрямку осі координат, то проекція на вісь ОХ дорівнює модулю вектора, взятого зі знаком «-».

 Учитель фізики

Хто пам’ятає, який рух називається рівномірним прямолінійним?

(- Якщо тіло за рівні проміжки часу здійснює однакові переміщення, то такий механічний рух називається рівномірним прямолінійним)

Напрям швидкості збігається з напрямом переміщення такого руху (V=S/t) Але частіше всього в житті ми спостерігаємо рух, швидкість якого змінюється.

(Відео: автомобіль набирає швидкість; потяг зупиняється; спортсмен на біговій доріжці набирає швидкість; діти катаються на лижах чи санках з гірки)

Проведемо дослід: кулька котиться по жолобу,який встановлений під кутом 30⁰, 45⁰ (час руху кульки вимірюємо в обох випадках і порівнюємо)

Висновок : (роблять учні) швидкість руху кульки збільшується  при більшому нахилі жолоба. Кажуть, що кулька рухається з більшим прискоренням.

Прискорення – це векторна фізична величина, яка характеризує швидкість зміни швидкості руху тіла і дорівнює відношенню зміни швидкості руху тіла до інтервалу часу, за який ця зміна відбулася.

а = (V-V₀)/t  a-прискорення,

 V₀-початкова швидкість,

 V-швидкість руху тіла через інтервал t 

Якщо рух спроектувати на вісь ОХ, то матимемо таку формулу: 

а _х= (V_х-V_0х)/t В СІ прискорення вимірюється в м/с².

Охарактеризуйте рух тіл, дописуючи слова в картки контролю засвоєння знань.

Слайд 6

 

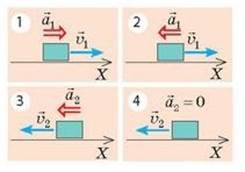
№2

1)    Швидкість руху тіла (збільшується), так як прискорення і швидкість (спів направлені).

2)    Швидкість руху тіла (зменшується), так як прискорення і швидкість (протилежно направлені).

3)    Це (рівномірний прямолінійний) рух.

VI.            В 9 класі ми будемо розглядати найпростіший вид руху – рівноприскорений прямолінійний рух.

Формулюємо і записуємо означення.

Рівноприскорений прямолінійний рух – це рух, під час якого тіло рухається прямолінійною траєкторією з незмінним прискоренням.

 Охарактеризуємо          графік         залежності а_х(t)   для рівноприскореного прямолінійного руху:   

Слайд 7

 

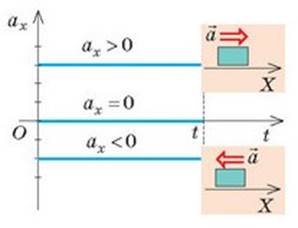
Графік залежності  а_х(t) для рівноприскореного прямолінійного руху.

 

VII.        Що можна сказати про швидкість в різні моменти часу?

(- вона різна)

Тому фізики ввели поняття миттєвої швидкості. Миттєва швидкість – це швидкість руху тіла в даний момент часу.

Виведемо формулу миттєвої швидкості: 

а=(V-V₀)/t,    V-V₀=аt,   V=V₀+аt      або       V_х=V_0х+а_х t  (лінійна функція)    Отже, щоб знайти миттєву швидкість руху тіла, необхідно мати початкову швидкість V_0х і прискоренняа_х.

Наприклад: 

Рівняння проекції швидкості має вигляд: V_x=15-5t

Тут  V_0х=15м/с, а_х=-5м/с², знак «-» показує, що напрямок прискорення протилежний напрямку осі ОХ.

Розглянемо і охарактеризуємо графіки залежності Vx(t) для рівноприскореного руху:

Слайд 8

 

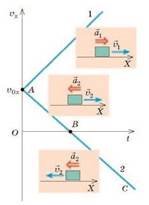
Графіки залежності Vx(t) для рівноприскореного руху.

 

Тіло 1  весь час збільшує швидкість руху, прискорення і швидкість за напрямком співпадають. У тіла 2 швидкість зменшується, прискорення і швидкість протилежно направлені.  В точці R тіло зупиняється  (V=0),  а потім його швидкість починає збільшуватись, рухаючись в протилежному напрямку.

VIII.Підсумок уроку. 

Сьогодні на уроці ви ознайомились з рівноприскореним прямолінійним рухом. Що це за рух? Що таке прискорення? Яка одиниця вимірювання прискорення в СІ? Який вигляд має рівняння залежності V(t) для рівноприскореного прямолінійного руху? Як називається ця швидкість? Яка тема з курсу алгебри була для вас опорною? ІХ. Домашнє завдання: параграф 28- опрацювати, ст..190, задача 2-письмово.

             

2.3. ІНТЕГРОВАНИЙ  УРОК ФІЗИКИ ТА МАТЕМАТИКИ

Тема. Переміщення під час прямолінійного рівноприскореного руху. Рівняння координати. Площа трапеції. Квадратична функція.

Мета: - сформувати знання учнів про фізичні величини, які описують         рівноприскорений рух, переміщення та координату, використовуючи знання з математики про квадратичну функцію та площу трапеції.

- розвивати пізнавальну активність і творчі здібності учнів.

Хід уроку

I.                  Організаційний момент.

II.               Формування теми, мети і завдань уроку.

Учитель фізики. Хто мріє працювати в Державтоінспекції, чи юристом, чи слідчим, необхідно вміти визначати гальмівний шлях транспорту, за яким можна знайти його швидкість та прискорення руху. Розібратись в цій темі нам допоможе цариця всіх наук – математика. Недарма кажуть, що математика – це мова фізики.

III.           Учитель математики. Нещодавно ми закінчили вивчати квадратичну функцію, її властивості та графік. Отже, коротко повторимо основні моменти. 

Слайди 1-4 (учні оголошують формулу квадратичної функції, її властивості, та дають характеристику графікам на слайдах)

 

Також для вивчення сьогоднішньої теми з фізики Вам необхідно згадати таку геометричну фігуру як трапеція, її елементи та формулу площі. Розглянемо чотирикутник АВСD. 

Слайд 5

 

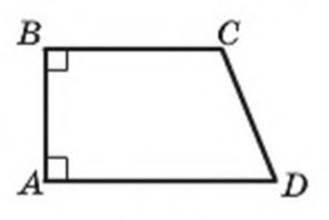
Хто пам’ятає  означення та формулу площі цієї геометричних фігури?

-            (Цей чотирикутник – трапеція, так як дві її сторони паралельні і дві не паралельні.

-            Формула площі:   S=) 

IV. Учитель фізики. А тепер, використовуючи раніше вивчений матеріал з математики, перейдемо до рівноприскореного прямолінійного руху і виведемо формулу переміщення і рівняння координати руху. Для цього зобразимо першу чверть системи координат, позначимо на осі ОХ час руху t, в с, а на осі ОУ – швидкість V, в м/с. Нехай в початковий момент часу тіло мало швидкість 15 м/с. З часом швидкість зменшувалась. Дослідимо зміну швидкості за 7 с руху.

Рисунок

Основи трапеції – це швидкість руху: V1  = 15 м/c,  V2  = 7,5 м/с. Висота трапеції – це час руху тіла: t = 7 с. Якщо спроектувати графік швидкості на вісь ОХ, то матимемо трапецію, площа якої чисельно дорівнює проекції переміщення.          

S  =   

Запишемо у вигляді формули:    Sx  Це формула проекції

переміщення. Вона показує геометричний смисл переміщення і справджується для будь-якого рівноприскореного руху.

Нагадаємо з минулого уроку формулу швидкості для рівноприскореного прямолінійного руху.

-         (V_х = V_0x+a_xt)  ②

Учитель фізики. У формулу ① підставимо формулу ② і спростимо отриманий вираз . Пропоную ці перетворення виконати бажаючому учневі. 

0_xt + a_xt²/2, маємо вихідну формулу: 

S_X= V_0xt + a_xt²/2 – це формула для визначення проекції переміщення через початкову швидкість руху тіла та через прискорення).

Так як V0x та а_х є фіксованими величинами, то переміщення залежить від часу. 

Наприклад: нехай  V_0x = 3м/с ,  а_х = 2м/с², тоді S_x = 3t + 2t². Це квадратична функція, її графіком є парабола. Проаналізуємо графіки на даних рисунках. 

 

Слайд 6 

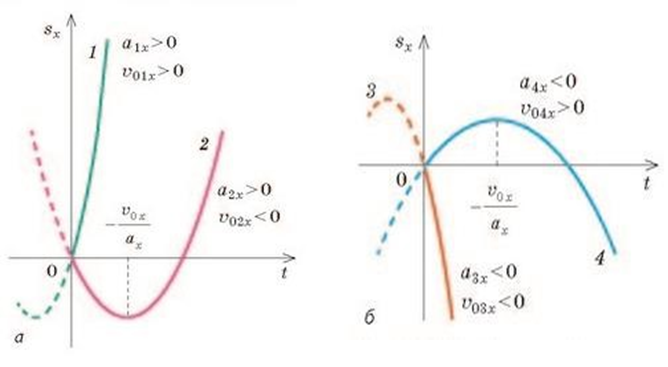
-         (Якщо прискорення додатне, то вітки параболи підняті вгору…)

Учитель фізики. Вершина параболи вказує на точку розвороту тіла. В точці розвороту можна знайти час розвороту тіла, замінивши у формулі  V_х=V_0х+а_х t   

V_0х на 0:                   V_0х+а_х t =0 ;                а_х t = - V_0х ;                 t = - V_0х/ а_х

Якщо в умові задачі не йдеться про час руху тіла і не потрібно його шукати, то запишемо формулу переміщення без врахування часу. Як вам уже відомо,  а_х = (V_х-V_0х)/t  ,  S _х  t 

Пропоную бажаючому учневі виразити з кожної формули час, прирівняти отримані формули і вивести формулу для проекції переміщення без врахування часу. 

-(… S_x = (V_x² – V _0x² )/2a_x )

Учитель фізики.  Запишемо рівняння координати тіла. Розглянемо рисунок.  Слайд 9

 

 

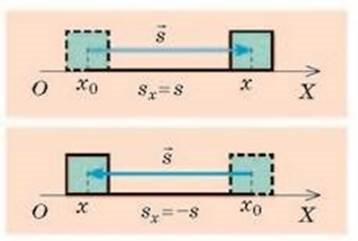
S_x = X – X₀ → X = X₀ + S_x ③ 

В рівняння ③ підставимо S_X  =  V_0x t + (a_х t² )/2 і отримаємо: X = X₀ + V_0xt + a_xt²/2 – рівняння координати.

Залежність координати від часу є квадратичною функцією, графіком якої є парабола.

                          V.      Закріплення.

Вправа 29, №4

Рівняння координат двох тіл, які рухаються вздовж осі ОХ, мають вигляд:  х₁  =  8 – 2t + t² ; x₂ = - 2 – 5t + 2t². 

1)    Для кожного тіла визначте: а) яким є його рух; б) початкову координату, модуль і напрямок початкової швидкості,  прискорення руху. 

2)    Знайдіть час і координату зустрічі тіл.

3)    Для кожного тіла запишіть рівняння Vx(t) і Sx(t), побудуйте графіки проекцій швидкості та переміщення.

Розв'язання.

1)    а) Це рух прямолінійний рівноприскорений.

         б) х₁  =  8 – 2t + t²,  (X = X₀ + V_0xt +( a_xt² )/2) → х₀ = 8м, V₀₁ = -2 м/c,              а_х = 2 м/с²              x₂ = - 2 – 5t + 2t²→ х₀ = - 2м, V₀₁ = - 5 м/c, а_х = 4 м/с²

2)    В момент зустрічі тіл х₁ = х₂ → 8 – 2t + t² = - 2 – 5t + 2t², t₁ = 5с, t₂ = -2с -

- що не задовольняє умові задачі. Отже, t = 5с.

3)    V_х = V_0x+a_xt → V₁ = -2 + 2t;   V₂ = -5 + 4t .

 S_X= V_0xt +( a_xt² )/2   →  

VI.            Підбиваємо підсумки:

повторюємо формули проекції переміщення, рівняння проекції переміщення та його графік, формулу координати тіла.   

VII.        Домашнє завдання: параграф 29 – опрацювати, вправа 29, №3 - письмово; проаналізувати розв’язання задачі 2 з п. 4. 

 

4. Про картки контролю засвоєння знань.

     Інколи я викладаю математику та фізику в одному і тому ж класі. Тому подібні бінарні уроки провожу досить часто: перед поясненням нової теми з фізики згадуємо відповідні закони чи теореми з курсу алгебри або геометрії. Чи, навпаки, вивчаючи програмний матеріал з алгебри або геометрії , знайомлю учнів з його практичним використанням  у фізиці, хімії, архітектурі і т. п.

      На уроках засвоєння нових знань використовую картки контролю засвоєння знань. Ці картки готую завчасно, або перед уроком учні отримують чисті аркуші. Все залежить від заготовлених питань. В ході пояснення нового матеріалу школярі, крім записів у зошитах, відповідають на питання з карток у певні моменти уроку. 

     Після останнього запитання картки здають учителю.  Їх можна оцінювати всі. А можна лише оцінити окремих учнів, за розсудом учителя. 

     Використовуючи картки контролю засвоєння знань, впевнилась в тому, що вони активізують та концентрують увагу учнів, понижують розумове напруження, привчають виділяти головне, робити висновки зі сказаного учителем, чи з прочитаного в підручнику. 

Переважна більшість учнів засвоює матеріал (звичайно на різному рівні), завдяки карткам. Тому раджу впроваджувати цей метод під час вивчення нового матеріалу з будь-якого предмету.

 

 

 

           

2.4. ІНТЕГРОВАНОГО УРОКУ З МАТЕМАТИКИ І ФІЗИКИ ( групові форми роботи, інтерактивна технологія «Ажурна пилка»)

Тема уроку :  “Закон Ома для ділянки кола. Математика чи фізика?

(Розв'язування графічних і розрахункових задач на закон Ома для ділянки кола)»

Тема: “Закон Ома для ділянки кола. Математика чи фізика?

(Розв'язування графічних і розрахункових задач на закон Ома для ділянки кола)»

Девіз уроку: «Природа формує свої закони мовою математики»

Дж.Максвелл Обладнання: мультимедійна система, індивідуальні картки різнорівневих завдань, портрети вчених-фізиків, електротехнічні комплекти для дослідження закону Ома для ділянки кола.

Тип уроку: інтегрований урок (математики і фізики) розв’язування задач Мета уроку:

а) навчальна:

●       Формувати вміння розв’язувати графічні і розрахункові, типові і нестандартні задачі на закон Ома для ділянки кола, поглибити, скорегувати знання про силу струму, напругу, опір та зв’язок між ними;

●       Узагальнення і застосування знань про пряму та обернену пропорційсть

●       переконатися в значущості знань, одержуваних на уроках математики, їх прикладному характері і ефективності використовування при розв’язанні фізичних задач.

б) розвивальна:

●       Розвивати уміння застосовувати теоретичні знання при розв’язуванні практичних задач;

●       Формування сприйняття єдності математичних моделей і фізичних процесів;

●       Розвиток уміння встановлювати зв’язок між силою струму і напругою, силою струму і опором, порівнювати, аналізувати, зіставляти, встановлювати причинно-наслідкові зв’язки;

●       Розвиток логічного мислення, стійкої уваги, математичної мови. в) виховна:

●       Мотивація учнів на активний підхід, інтерес до вивчення фізики і математики;

●       Виховувати культуру спілкування, толерантність, впевненість у собі; ● виховувати навички індивідуальної і колективної роботи; ●Сприяти цілісному розумінню навколишнього світу.

Очікувані результати: 

Учні 

✔   Поглиблять знання про силу струму, напругу опір, закон Ома для ділянки кола;

✔   Навчаться розв’язувати комплексні, графічні задачі на закон Ома для ділянки кола;

✔   з’ясують залежність між фізичними та математичними величинами, їх взаємозв’язок;

✔   підвищать інтерес до вивчення фізики і математики;

✔   виконають завдання контрольної роботи. Організація класу, початок уроку. Мотивація навчальної діяльності Учитель фізики:

На дошці ви бачите незвичайний дріб (чисельник – портрет Вольта, знаменник – портрет Ома, частка – портрет Ампера). Упізнайте вчених на портретах і розшифруйте цей дріб.

Звучать фанфари.

До нас завітали шановні синьйор Вольта, Ом, мсьє Ампер.(вчені розповідають про свої досягнення і сперечаються, хто головніший. Ом запитує учнів класу закон Ома, вони відповідають).  

Учитель фізики

Так, дійсно закон Ома дуже важливий. Він відповідає на питання «Від чого і як залежить сила струму в провіднику. Це важливо, бо саме від сили струму залежать дії струму: теплова, механічна, магнітна, хімічна, світлова. А саме дії струму і застосовує людина в різноманітних побутових приладах, технологічних процесах. Без цього закону не обійтись при розрахунках електричних кіл ( ми це будемо робити на наступних уроках). Закон Ома є основою всієї електротехніки, а уявити наше життя зараз без електричного освітлення взагалі неможливо учні пояснюють дії струму, які лежать в основі роботи приладів)

Формулювання мети уроку

Сьогодні ми будемо вчитися застосовувати набуті знання про головні електричні величини та закон Ома при розв’язуванні задач. Це головна мета уроку. Але визнаєте, що дуже часто вам заважає те, що ви не можете правильно застосувати математичний матеріал. А роль математики у фізиці величезна. Математичні та фізичні знання пов'язані, переплетені один з одним. Тому темою уроку є: «Закон Ома для ділянки кола. Математика чи фізика?(Розв'язування графічних і розрахункових задач на закон Ома для ділянки кола)»(записати  тему уроку).

 На уроці ви побачите на скільки глибокі зв'язки фізики і математики. Нам належить займатися розрахунками, згадати про перевід одиниць вимірювання фізичних величин в систему СІ, показувати уміння у вираженні компонентів з формул; звернутися до графічних залежностях величин (пряма і обернена пропорційності). І вже на допомогу  нам йде ваш учитель математики, без нього не обійтися. Учитель математики.

. Відомий такий вислів: „Математика–цариця всіх наук і служниця фізики”. Мені більше подобаються такі слова Іммануіла Канта «У будь-якій науці стільки істини, скільки в ній математики».  Сьогодні ми проведемо  урок, на якому повторимо і підсумуємо вивчене нами раніше з математики, навчимося використовувати його при розв’язуванні графічних і розрахункових задач на закон Ома для ділянки кола. Ми переконаємось  в значущості знань, одержуваних на уроках математики, їх прикладному характері і ефективності використовування при розв’язанні фізичних задач,  що математика і фізика не розмежовані науки, між ними існує тісна взаємодія: математика є інструментом вивчення фізичних явищ, а фізика ілюструє фізичну спрямованість математики, її значення у повсякденному житті.

Тільки усвідомлене використання знань, оволодіння математичним апаратом, уміння логічно мислити дозволить досягти успіхів у підкоренні вершин інших наук.  Нашим девізом будуть слова Декарта,  

 

математика	фізика
	Знати	уміти
Пряма пропорційна функція її властивості та графік Обернено пропорційна залежність, її властивості, та графік Визначати невідомі компоненти зі складних виразів	Сила струму, напруга , опір(визначення, формула, одиниці, прилад для вимірювання)   Закон Ома для ділянки кола	Обчислювати силу струму, напругу, опір з формул і графічно   Будувати графіки залежностей сили струму від напруги, сили струму від опору)

 

Учитель фізики

Наш урок сміливо можна назвати МіФом (математика і фізика) Актуалізація опорних знань.

Учитель математики

Для успішної реалізації мети уроку нам треба пригадати деякі математичні поняття. Ключовим з них є функція. Функція виражає залежність між величинами. Кожна область знань: фізика, біологія, географія, соціологія і т.д. мають свої об’єкти вивчення, встановлюють взаємозв’язок цих об’єктів. Математика розглядає абстрактні змінні величини і в «відхіленому» вигляді вивчає різні закони їх взаємозв’язку, які на математичній мові називаються функціональними залежностями або просто функціями. Наприклад, у співвідношенні у=к/х математик бачить абстрактну пряму пропорційну залежність, а фізик може встановити в ньому залежність сили струму від напруги і просто замінити позначення змінних загально прийнятими. Тому в цьому питанні математика є базою, основою фізики. Витягнемо з глибин своєї пам’яті знання про ті функції, які потрібні для вивчення закону Ома для ділянки кола, а саме пряму пропорційну залежність і обернену пропорційність.

Учитель фізики

                Розглянемо     застосування    прямої     і    оберненої     пропорційностей    при

розв’язуванні задач на закон Ома для ділянки кола

Інтерактивна вправа «Доміно»

Учні отримують картки з початком і продовженням речень.

1.     Що таке сила струму?

2.     Одиниці сили струму?

3.     Формула сили струму?

4.     Прилад для вимірювання сили струму?

5.     Що таке напруга?

6.     Одиниці напруги?

7.     Формула напруги?

8.     Прилад для вимірювання напруги?

9.     Що таке опір?

10.Одиниці опору?

11.Формула опору? Від чого він  залежить? Що це означає?

12.Одиниці виміру всіх величин?

13.Похідні формули?

14.Сформулюйте закон Ома для ділянки кола

15.Напишіть його на дошці

16.Похідні формули

Аналіз інсталяції «закон Ома» (вкладка)

Проаналізуємо дані таблиці (два учня біля дошки: фізик і математик1.Математику – прочитати залежність, фізику – знайти відповідну залежність у формулі закона Ома

Математика	Фізика
у=кх;	І=U/R;  I=1/RU
У – функція Х – аргумент K – коефіцієнт	І – ? U– ? 1/R - ?
Графік у(х) – пряма	?
y=к/x;	І=U/R,
y x k	I R U
Графік – гіпербола	?

Графіками математичних залежностей у (х) є пряма і гіпербола

Які можна зробити висновки щодо графіків залежностей I I(U) та I(R)?

Висновок(учні): математика є базою фізики, тільки в математиці абстрактні величини, а в фізиці – конкретні фізичні. Графіками залежностей сили струму від напруги і сили струму від опору повинні бути пряма і гіпербола і будувати їх потрібно за тими ж правилами , що і в математиці.

Розв'язування задач

1.Розв'язування графічних задач

Метод «Ажурна пилка»

Клас напередодні  поділено на 4 «різнокольорових» групи. Кожен учень отримав картку певного кольору з номером на ній (від одного до чотирьох). Групи отримали певні завдання. 

Математики:

«Червоні» - ввести поняття функції, аргументу, графіка, прямої пропорційної залежності.

«Сині» - ввести поняття функції, аргументу, графіка, обернено пропорційної залежності.

Фізики:

«Жовті» - ввести поняття сили струму, напруги, опору, буквені позначення, одиниці вимірювання, залежність сили струму від напруги при незмінному опорі.

«Зелені» - ввести поняття сили струму, напруги, опору, буквені позначення, одиниці вимірювання, залежності сили струму від опору при постійній напрузі.

Учні в «кольорових» групах отримують графічні задачі:

Математики:

«Червоні»  - Побудувати графік залежності  у=4х в І координатній чверті. «Сині»  - Побудувати графік залежності у=6/х в І координатній чверті. Фізики;

«Жовті» - Побудувати графік залежності сили струму від напруги для споживача, опір якого 0.25 Ом.

«Зелені» - Побудувати графік залежності сили струму від опору при напрузі 6В

В «домашніх» групах учні обмінюються інформацією, розв'язують задачі, допомагають один одному.

Учитель  пропонує учням об’єднатися в групи відповідно до своїх номерів –

«експертні» групи. В кожну «експертну» групу входять представники з кожної «домашньої» групи. Учні записують формули, розв’язують задачі кожного іншого типу, знаходять спільне, відмінне.

Учні об'єднують знову в домашні групи, обмінюються інформацією. 

Чотири представника кожної групи розв'язують задачі біля дошки,

Порівнюють отримані графіки,  роблять  висновки щодо відповідності математичних та фізичних задач.

2.Розв’язування обернених задач(Слайди№17,18,19,20)(усно) 3.Розв'язування комплексних задач під контролем учителя.

Клас поділено на 3 різнорівневих групи. Задачі написані на картках. По одному учню з кожної групи працюють біля дошки.

Середній рівень

Визначте силу струму в електрочайнику, ввімкнутому в мережу з напругою 220 В, якщо опір нитки розжарювання дорівнює 40 Ом.

Достатній рівень

Скільки метрів нікелінового дроту перерізом 0.1 мм²потрібно для виготовлення реостата опором 180 Ом?(ῥ=0,42Ом·мм²/м)

Високий рівень

По нікеліновому дроту довжиною10 м йде струм силою 0,5 А. Визначте переріз провідника, якщо до його кінців прикладена напруга 20В.(ῥ=0,42Ом·мм²/м) Підсумки уроку.

 

             

ВИСНОВКИ

Провівши інтегрований урок, учитель підвищить мотивацію навчання учнів, створить умови для практичного застосування раніше отриманих знань з курсу шкільних предметів. Отже, в результаті, буде досягнута головна мета інтегрованого уроку – створені умови мотивованого практичного застосування знань, навичок та вмінь.  Школярі матимуть можливість систематизувати отримані знання, поглибити їх, поділитись ними.

Під  час  проведення  інтегрованого уроку учні активно співпрацюють з учителем. У представлених уроках школярі діляться своїми знаннями в ході знайомства з новою інформацією, виконують алгебраїчні перетворення для виведення робочих формул з фізики, після кожного етапу уроку осмислюють та узагальнюють нові знання.

Для практичного використання отриманих знань учні на кожному етапі виконують різні задачі та вправи усного чи письмового характеру. На двох уроках, представлених до вашої уваги, школярі заповнюють картки контролю нових знань, за допомогою яких учитель зможе оцінити ступінь засвоєння нової теми. І, в результаті, на наступному уроці знатиме, на що потрібно звернути увагу ще раз. 

Спостереження → Думка → Дослідження → Знання

Геракліт	Єн штейн	Л. да Вінчі
… довіряти нерозумним відчуттям – властивість грубих душ	…наука - це неустанна багатовікова робота думки об’єднати  разом засобом системи всі пізнавані явлення нашого світу	… знання не провірені дослідженнями, належності  до  дійсності, безнадійні і мають безліч помилок  помилками

 

Перед початком уроку завжди потрібно ставити якісь завдання та намагатися на них відповісти.  Наприклад:

3. Які закономірності ви вже помітили в природі?  Ви це - закономірності?  Чому?  Враховуєте впевнені, що ці закономірності у повсякденному житті?  Як Ви враховуєте?  

2        .  Які небезпеки загрожують нашій планеті?  Чи можете ви особисто взяти участь у спасінні Землі?  Що для цього роблять люди?  Хто ж наражає Землю на небезпеку?  (Обговоріть із батьками.) 

3        Чи вірите ви в чудеса?  А що це таке – диво?  Ви бачили хоча б одне диво?  Розкажіть, це цікаво!  Які «чудеса» подарувала людям наука?    

Отож, вважаю доцільним проводити інтегровані уроки, тому що досягнути мети якісної освіти можна шляхом вивчення нових педагогічних технологій та удосконаленням застарілих методик.  

           

ЛІТЕРАТУРА

1.        Островерхова Н. М. Аналіз уроку: концепції методики, технології. К: Фірма «Інкос», 2003, с.331

2.        Козлова О. Г. Методика Інноваційного пошуку вчителя. – Суми. ВВП

«Мрія - 1», ЛТД, 2005

3.        Методика проведення бінарних уроків як однієї з форм реалізації між

предметних зв’язків. Мельник І. В. //  Published on Feb 2. 2015                             

4.        О. В. Григорович. Хімія, 8 клас. Видавництво «Ранок», 2016, с.256

5.        В. Г. Бар'яхтар, С. А. Довгий. Фізика,  9 клас.  «Ранок», 2017, с.276

6.        О. С. Істер. Алгебра, 9 клас. Київ, «Генеза», 2017, с.264

7.        Бінарний урок з фізики. // Klasnaocinka.com.ua

8.        Бугров В. А., Іванов А. І., Сверидов В. І. Фронтальні експериментальні завдання по фізиці. 9 кл.: Дидактичні матеріали. – М.: Просвіта, 1986