Сума кутів опуклого многокутника. Різні способи доведення відомої теореми.

Галина Дудар

Вчитель-методист.

м. Тернопіль,

ТЗОШ І-ІІІ ступенів №19

9 клас.

Теорема про суму кутів опуклого чотирикутника. Різна способи доведення

Усім відома теорема про суму кутів опуклого чотирикутника формулюється наступним чином «Сума кутів опуклого многокутника обчислюється за формулою 180◦(n-2), де n-кількість сторін Звісно, у кожному із пропонованих підручників є доведення.

Один із способів доведення цієї теореми – метод математичної індукції. Звісно, цей метод можна показати дітям, які цікавляться математикою. Спочатку для n=3 ми маємо підтвердження теореми про суму кутів трикутника, далі припускаємо, що формула істинна для n=k, тобто 180◦(k-2). Після цього доведемо, що формула справедлива для n=k+1.

180◦(k+1-2) =180(k-2) +180. З останнього запису робимо висновок, що сума кутів опуклого многокутника обчислюється за формулою180◦(n-6). Доведення цієї теореми можна запропонувати учням у групах, роздавши їм наступні

завдання:

1.Розділити довільний n-кутник, наприклад (n=6, 7, 5) на трикутники,

провівши діагоналі з однієї вершини.

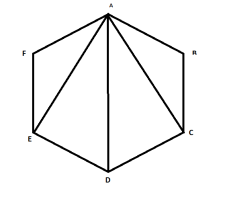
Учні помітять, що кількість трикутників буде на 2 менша за кількість сторін, тобто n-2, тому сума усіх кутів многокутника буде 180ᵠ( n-2).

2. Розділити довільний многокутник на трикутники, взявши довільну точку М всередині нього.

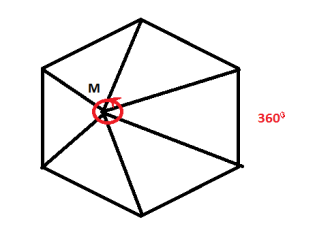
У даному випадку бачимо , що n-кутник розділився на n трикутників, сума кутів кожного з яких 180◦, тому потрібно відняти суму кутів із вершиною у внутрішній точці М n-кутника, тобто 360◦. Отримаємо 180◦n-360◦=180◦(n-2).

3. Цікаве наступне доведення. Добудуємо у многокутнику зовнішні кути. Вибравши довільну точку за вершину  на іншому рисунку відкладемо кути, рівні зовнішнім кутам даного n-кутника. Враховуючи, що кожна сторона утворює розгорнутий кут із зовнішнім (їх є рівно n), маємо

180◦n-360◦=180◦(n-2), що й треба було довести.

.

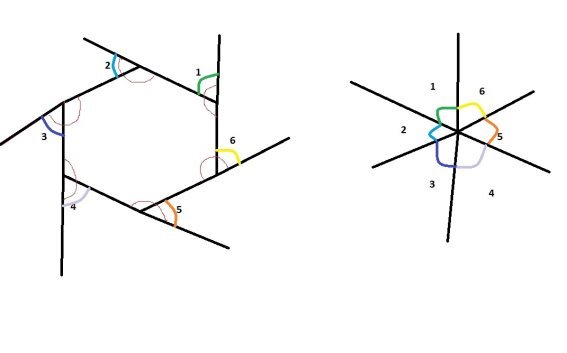
 Що стосується останнього способу, пропоную учням накреслити n-кутник на цупкому папері, продовжити сторони і вирізати утворені зовнішні кути, помістити їх у одну точку, аби переконатися що їх сума насправді дорівнює 360◦ ( до слова, це наочне нестроге доведення теореми про суму зовнішніх кутів опуклого n-кутника, взятих по одному при кожній вершині). Матимемо візуалізацію теми. Що стовідсотково сприятиме кращому засвоєнню матеріалу теми і спонукає до пошуку різних шляхів доведення математичних фактів.