Презентація "Вписані і описані чотирикутники"
Про матеріал
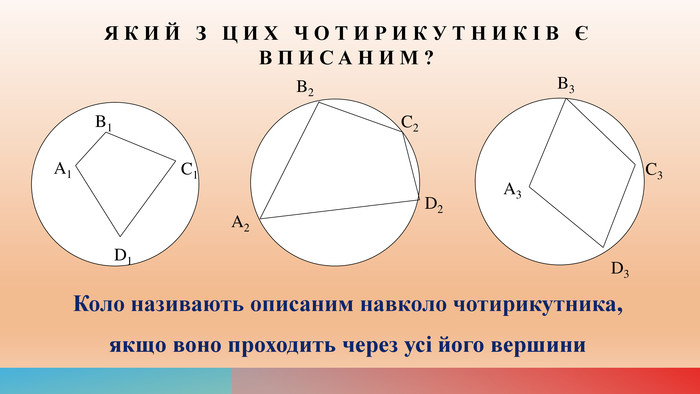
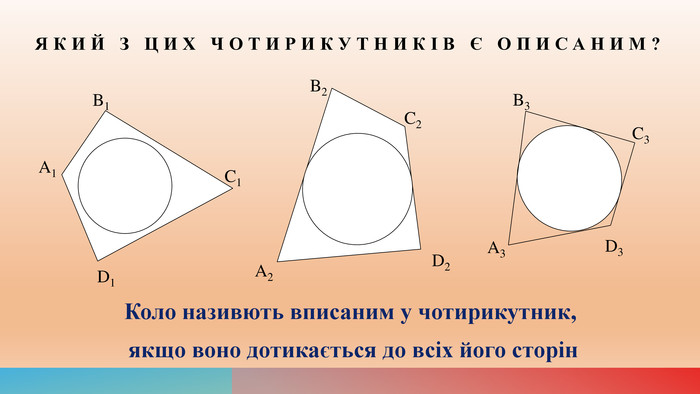
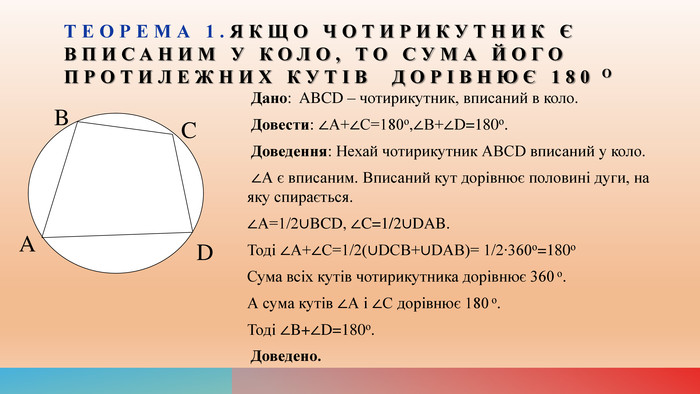
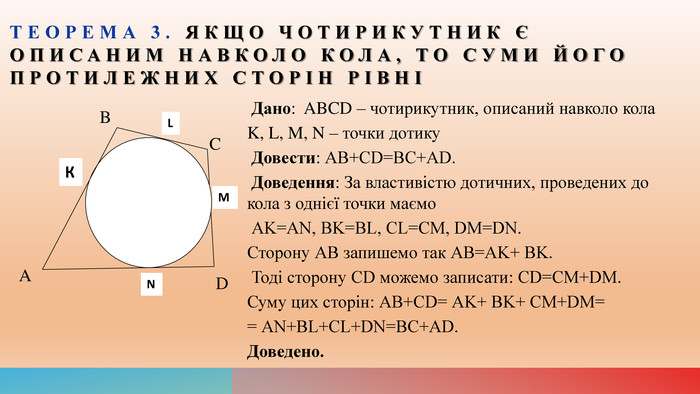
Вивчення теми "Описане та вписане кола чотирикутника". Теоретичний матеріал до вивчення п. 10 підручника "Геометрія" 8 клас, автори А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


















-

Чичиль Дмитро Валерійович
25.11.2024 в 22:34
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Ліпич Надія
18.11.2023 в 15:00
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Андрейченко Тетяна Олексіївна
12.11.2023 в 22:08
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Доренська Наталія Антонівна
08.11.2023 в 15:07
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Шатковська Оксана
30.11.2021 в 21:30
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 2 відгука