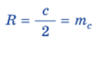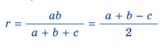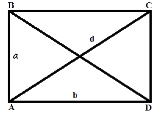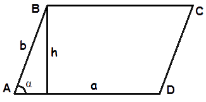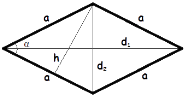Елементи продуктивного навчання на уроках математики (таблиці та задачі для 9 класу, геометрія)

 

 

Методичні матеріали

вчителя математики

вищої кваліфікаційної категорії,

старший вчитель

ЛГ «Престиж»

Шевченківського району

Боднар Оксани Степанівни.

 

 

Львів 2022

ЗМІСТ

ВСТУП

ТРИКУТНИКИ

Прямокутний трикутник

Рівносторонній трикутник

Рівнобедрений трикутник

Довільний трикутник

ЧОТИРИКУТНИКИ

КВАДРАТ і його властивості

ПРЯМОКУТНИК і його властивості

ПАРАЛЕЛОГРАМ і його властивості

РОМБ і його властивості

ТРАПЕЦІЯ та її властивості

КОЛО та КРУГ

ВИСНОВОК

ЛІТЕРАТУРА

ВСТУП

На уроках геометрії впроваджую технологію інтенсивного навчання на основі схемних і знакових моделей навчального матеріалу за Шаталовим.

Принципи технології інтенсифікації навчання В. Ф. Шаталова: багаторазове повторення; обов’язковий поетапний контроль; блочне вивчення матеріалу; динаміка діяльності; використання опор.

Технологічні етапи:

· перший – вивчення теорії у класі;

· другий – самостійна робота вдома;

· третій – перше повторення – фронтальний контроль засвоєння конспекту;

· четвертий – усне проговорювання опорного конспекту (це необхідний етап мовленнєвої діяльності при засвоєнні матеріалу, що реалізується під час різних видів опитування);

· п’ятий – друге повторення: узагальнення і систематизація; взаємоопитування та взаємодопомога; ігрові елементи (змагання команд, розв’язування ребусів тощо).

Прогнозовані результати:

- формування системи знань, умінь, навичок;

- навчання всіх дітей незалежно від індивідуальних даних;

- прискорене навчання.

Український учитель-новатор В.Ф. Шаталов завдяки широкому використанню опорних схем конспектів домагався високих результатів у навчальній діяльності. Він широко використовував різні види опорних схем, опорних сигналів та опорних конспектів у процесі пояснення нового навчального матеріалу безпосередньо на уроці, а потім учні використовували ці прийоми під час виконання різних видів домашніх завдань і самостійно моделювали опорні схеми. В основі цієї роботи лежали певні закономірності про особливості конкретно-образної пам'яті та психологічні асоціації.

Методика В. Ф. Шаталова суттєво економить час уроку, дає можливість приділяти більше уваги формуванню вмінь і навичок учнів, застосовувати здобуті знання на практиці. Однак для розробки опорних сигналів необхідно використовувати особливі позначення, рисунки, символи, схеми, таблиці, які мали б нагадувати про конкретні приклади чи факти. Тому без пояснення вчителя та свідомого використання підручника учень не може самостійно засвоїти навчальний матеріал лише за опорними сигналами.

Структурно-логічні схеми будуються на принципі структурування навчальної інформації, без якої неможливо формувати в учнів уміння аналізувати, порівнювати, абстрагувати, узагальнювати .

Основне призначення структурно-логічної схеми  - доведення до учня логіки організації навчального матеріалу на уроках. Основні труднощі в засвоєнні і практичному застосуванні вивченого матеріалу – це виділити головне, побудувати логічну схему матеріалу і на основі цього визначити підходи до вирішення завдань.

 

Етапи послідовного складання структурної схеми.

1 етап: пояснення нового матеріалу методом розповіді із застосуванням звичайних методів навчання;

2 етап: стисле пояснення з опорною схемою на аркушах;

3 етап: докладне опитування 2-х,3-х учнів за схемою (без оцінювання;

4 етап: переписування схем у зошит;

5 етап: розфарбування схем вдома;

6 етап: читання матеріалу в підручника;

7 етап: запам'ятовування;

8 етап: письмове відтворення схеми на наступному уроці;

9 етап: усні відповіді за опорним конспектом біля дошки.

Отже, матеріал сприймається учнями після 7-9-ти разового повторення. Для слабких учнів кількість повторень повинна бути більшою, доки учень і учитель не будуть упевнені у позитивній відповіді.

У зошиті довіднику з геометрії для учнів 7-9 класів подані основні формули та властивості геометричних фігур, вправи для закріплення матеріалу ( апробовані та використані при складанні опорних конспектів на моїх уроках)

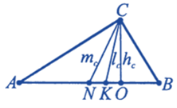
ТРИКУТНИКИ

Прямокутний трикутник

Малюнок і позначення	Формули
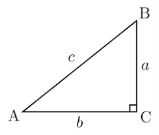
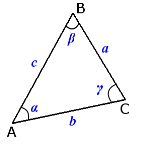
	1.Кути  ∠С=90° (прямий) ∠А +∠ В =90° (сума гострих кутів = 90°) ∠A+∠B+∠C=180°
	2.Периметр Р= а+b+c
	3 Теорема Піфагора c2=a2+b2
	4.Площа
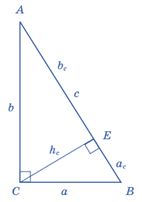
	5. Медіана, проведена до гіпотенузи
	6.Радіус описаного кола
	7. Радіус вписаного кола
	8. Тригонометричні функції
	9. Катети та їх проекції на гіпотенузу

Вправи

1. Катети прямокутного трикутника 12см та 16см.Знайти  периметр, площу, висоту, медіани  трикутника ,радіуси вписаних та описаних кіл.
    
2. Гіпотенуза прямокутного трикутника дорівнює 10см ,а косинус одного з гострих кутів – 0,8. Знайти катети, периметр, площу, висоту трикутника, радіуси вписаних та описаних кіл.
    
3. Висота прямокутного трикутника ,проведена до гіпотенузи, ділить її на відрізки 2см та 18см. Знайти катети, периметр, площу, висоту трикутника ,радіуси вписаних та описаних кіл.
    
4. Медіана прямокутного трикутника, проведена до гіпотенузи, дорівнює 10см,а відстань між серединою гіпотенузи та основою висоти ,проведеної до гіпотенузи, дорівнює 6см. Знайти катети, площу, висоту трикутника, радіуси вписаних та описаних кіл.

 

 

 

Рівносторонній трикутник

Малюнок і позначення	Формули
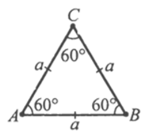
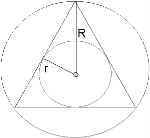
	1.Кути  ∠А =∠ В =∠С=60° ∠A+∠B+∠C=180°
Р - периметр	2.Периметр Р= 3а
h = m = l	3 Висота =медіана =бісектриса
S – площа	4.Площа Sтрикутника= (a2*√3 )/4
	5.Радіус описаного кола                                  R=a/√3
	6 Радіус вписаного кола   r=a/2 √3
	Зауваження R=2r , . h=R+r

 

Вправи

1. Сторона правильного трикутника 6см .Знайти периметр, площу, висоту, радіуси вписаних та описаних кіл.

 

2. Бісектриса рівностороннього трикутника дорівнює 3см. Знайти висоту, периметр, площу, радіуси вписаних та описаних кіл.

 

 

3. Радіус вписаного кола у правильний трикутник дорівнює 4см. Знайти периметр  , площу , висоту, радіус описаного описаних кола.

 

4. Сторона правильного трикутника 12 см. Знайти периметр та площу трикутника, вершинами якого є середина сторін даного.

 

 

 

 

Рівнобедрений трикутник

Малюнок і позначення	Формули
	1.Кути  ∠А  =∠В ,  АВ- основа (кути при основі рівні) ∠А+ ∠B+∠C = 180°
	2.Периметр(сума усіх сторін)  Р= а+а+с         b=a
	3 Висота =медіана =бісектриса,  проведині до основи, АВ-основа
	4.Площа Як у довільного трикутника
	5.Радіус описаного кола  Як у довільного трикутника
	6 Радіус вписаного кола  Як у довільного трикутника

 

Вправи

1. Основа та бічна сторона рівнобедреного трикутника відповідно дорівнюють 16см та 10см. Знайти периметр, площу, висоти, радіуси вписаних та описаних кіл.
   знайти косинус кута при основі.

 

2. Периметр рівнобедреного трикутника дорівнює 108 см, основа – 30см. Знайти висоти , площу ,радіуси вписаних та описаних кіл.

 

3. Висота проведена до бічної сторони рівнобедреного трикутника ділить її га відрізки 8см та 2см , починаючи від вершини трикутника. Знайти косинус кута при вершині ,площу  трикутника та радіус описаного кола.

 

4.  Бічна сторона рівнобедреного трикутника 6см, а висота проведена до основи, дорівнює 4см. . Знайти синус кута при основі ,площу  трикутника та радіус описаного кола.

 

 

 

Довільний трикутник

Малюнок і позначення	Формули
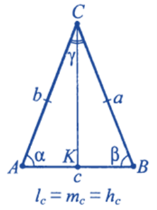
	1.Кути  ∠A+∠B+∠C=180°  ∠ВСК – зовнішній кут   1.якщо α > β, тоді a > b 2.нерівність трикутника a + b > c b + c > a c + a > b
	2.Периметр     Р = a + b + c
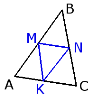
	3 Середня лінія MN = ½ AC      KN = ½ AB     KM = ½ BC MN || AC     KN || AB     KM || BC
S - площа трикутника, a, b, c - довжини сторін трикутника, h - висота трикутника, γ - кут між сторонами a и b, r - радіус вписаного кола, R - радіус описаного кола, p =  a + b + c   - півпериметр  2	4.Площа   S =   1 a · h 2 S = 1 a · b · sin γ 2 S = √p(p - a)(p - b)(p - c) S =  a · b · с 4R S = p · r
	5. Медіана-ділить навпіл протилежну сторону,  Бісектриса ділить навпіл кут трикутника, Висота – перпендикуляр (утворює кут 90 )
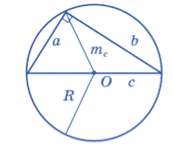
	6.Радіус описаного кола R = abc/4S
	7 Радіус вписаного кола r = S/p
	8 Теорема синусів a  =  b  =  c  = 2R sin α sin β sin γ
	9 Теорема косинусів c2 = a2 + b2 - 2ab·cos γ

 

Вправи

1. Сторони трикутника 9см, 10см,17см. . Знайти  периметр, площу,висоти трикутника ,радіуси вписаних та описаних кіл.Знайти косинус найменшого кута, медіану, проведену до середньої сторони, синус найбільшого кута трикутника.
    
2. Одна сторона трикутника 21см,а інші відносяться як 3:8 та утворюють кут 60.Знайти периметр, площу, радіуси вписаного та описаного кіл. Знайти висоти трикутника та медіану, проведену до найбільшої сторони.
    
3. Сторони трикутника, одна з яких на 2см більша за іншу, утворюють кут 120,а третя сторона дорівнює 7см. Знайти периметр,  площу,  висоти,  радіуси  вписаного та описаного кіл. Знайти висоти трикутника .
    
4. Бісектриса кути трикутника ділить сторону на відрізки, різниця яких дорівнює 2см. Дві інші сторони трикутника 6см та 9см. Знайти периметр, площу ,висоти ,синус найменшого кута , косинус найбільшого кута, радіуси вписаних та описаних кіл.

 

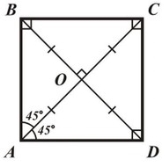
ЧОТИРИКУТНИКИ

КВАДРАТ і його властивості

Малюнок і позначення	Формули
	1.Кути  ∠А =∠ В =∠С=∠D=90° ∠A+∠B+∠C+∠D =360°
	2.Периметр P = 4a
	3 Діагоналі (за теоремою Піфагора) d = √2a (перпендикулярні ,рівні, діляться навпіл, є бісектрисами кутів)
	4.Площа S = a2 S =  d2 2
	5. Радіус описаного та вписаного кіл R = d/2 r = a/2

 

Вправи

 

1. Сторона квадрата 4см. Знайти діагональ , периметр, площу, радіуси вписаних та описаних кіл. Знайти відстань від точки перетину діагоналей до сторін та вершин квадрата. Знайти периметр чотирикутника , утвореного серединами сторін даного.

 

2. Сторона квадрата на 18 см менша від його периметра. . Знайти сторону, діагональ , периметр, площу цього  квадрата, радіуси вписаних та описаних кіл.

 

3. Периметр квадрата дорівнює периметру прямокутника зі сторонами 6см та 10см. Знайти сторону, діагональ , периметр, площу цього  квадрата, радіуси вписаних та описаних кіл.

 

 

4. У скільки разів збільшиться периметр  та площа  квадрата, якщо його діагональ збільшилась у 3 рази ? Як зміняться радіуси вписаних та описаних кіл?

 

 

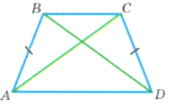
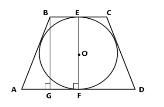
ПРЯМОКУТНИК і його властивості

Малюнок і позначення	Формули
	1.Кути  ∠А =∠ В =∠С=∠D=90° ∠A+∠B+∠C+∠D =360°
	2.Периметр (сума усіх сторін) P =  2(a + b)
Діагоналі рівні та точкою перетину діляться навпіл АО=ВО=СО=DO	3 Діагональ (за теоремою Піфагора) d = √a2 + b2
	4.Площа S = a · b
	5. Радіус вписаного кола Вписати коло не можливо
	6.Радіус описаного кола R =  d 2

Вправи

1. Сторони прямокутника 6см та 8 см. . Знайти діагональ,  периметр, площу, радіус  описаного кола. Знайти відстань від точки перетину діагоналей до більшої сторони. Знайти косинус кути між меншою стороною та діагоналлю.

 

2. Діагональ прямокутника дорівнює 12см ,а менша сторона 6см. Знайти кут між діагоналями, кут між діагоналлю та сторонами, кут між діагоналлю та бісектрисою кута. Знайти площу та  периметр .

 

3. Діагональ прямокутника дорівнює 25 см, а одна сторона на 17см довша за іншу. Знайти периметр, площу, радіус описаного кола, синус кута між діагоналями.

 

4. Перпендикуляр, проведений до діагоналі прямокутники,  ділить її на відрізки 4см та 9см.Знайти сторони прямокутника, площу, радіус описаного кола, тангенс кута між діагоналлю та більшою стороною. Знайти периметр та площу чотирикутника, утвореного серединами сторін даного.

 

 

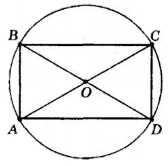
ПАРАЛЕЛОГРАМ і його властивості

Малюнок і позначення	Формули
	Кути ∠B + ∠A = 180°  ∠D + ∠C = 180° (кути ,що прилягають до однієї сторони =180° ) ∠А =∠С , ∠В=∠D (протилежні кути рівні)   ∠A+∠B+∠C+∠D =360°
	2.Периметр(сума усіх сторін)  P =  2(a + b)
Діагоналі не є рівними,  не є бісектрисами кутів, точкою перетину діляться навпіл АО=ОС ,ВО=ОD	3. Діагоналі паралелограма
S - площа паралелограма, a, b - довжини сторін паралелограма, h - довжина висоти паралелограма, d1, d2 - довжини діагоналей паралелограма, α - кут між сторонами паралелограма, γ - кут між діагоналями паралелограма.	4.Площа   S  = a · ha S = b · hb  S =a · b · sin α S = 1 d1d2 sin γ 2
	5. Радіус вписаного та описаного кіл Описати та вписати кола неможливо Не існують

 

Вправи

1. Висоти паралелограми 4см та 6см.,а кут між ними 30. Знайти кути, сторони, площу, периметр цього паралелограма.

 

2. Діагоналі паралелограма 12см та 10см, а кут між ними 60.Знайти сторони та площу фігури,.

 

3. Сторони паралелограма 15 см та 25см. Одна з діагоналей перпендикулярна до меншої сторони. Знайти периметр, площу, другу діагональ, висоти паралелограма.

 

4. Сторони паралелограма 9см та 12см., а сума двох нерівних висот 14 см. Знайти висоти ,периметр, ,площу , синус гострого кута паралелограма.

 

 

 

 

 

 

РОМБ і його властивості

Малюнок і позначення	Формули
	1.Кути ∠B+ ∠A = 180°  ∠D + ∠C= 180° Протилежні кути рівні ∠А = ∠C  ∠D=∠D ∠A+∠B+∠C+ ∠D=360°
	2.Периметр Р= 4а
	3 Діагоналі не є рівними, є бісектрисами. Діагоналі взаємно перпендикулярні, точкою перетину діляться навпіл АО=ОС ,ВО=ОD
S - площа ромба, a - довжина сторони ромба, h - довжина висоти ромба, α - кут між сторонами ромба, d1, d2 - довжини діагоналей.	4.Площа S = a · h S = a2 · sin α S = 1 d1 · d2 2
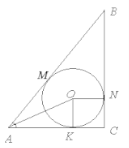
	5. Радіус вписаного та описаного кіл r = h/2   Описати коло неможливо

 

Вправи

1. Сторона ромба 6см, гострий кут 60 .Знайти решту кутів, периметр , площу, діагоналі,  висоту, радіус вписаного кола .

 

2. Один з кутів ромба 60, більша діагональ 24 см. Знайти решту кутів, периметр , площу ,діагоналі,  висоту, радіус вписаного кола .

 

3. Висота ромба 6см,більша діагональ 10см. Знайти радіус вписаного коло, площу та периметр ромба, ,тангенс гострого кута.

 

4. Точка дотику кола, вписаного в ромб ділить сторону на відрізки 4см та 9 см. Знайти   периметр , площу ,діагоналі,  висоту, радіус вписаного кола ,синус гострого кута.

 

 

 

 

 

ТРАПЕЦІЯ та її властивості

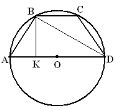
Малюнок і позначення	Формули
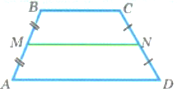
	1.Кути  ∠A+∠B+∠C +∠D=360°  ∠B + ∠А = 180°  ∠D + ∠C = 180° (Сума кутів, що прилягають до бічної сторони 180°) ∠А=∠D         ∠B=∠C (тільки у рівнобічній трапеціі )
a ,b - основи	2.Периметр (сума усіх сторін) Р= а+b+с+d
	3 Середня лінія МN=(a+b) /|2  МN паралельна АD,ВС    Якщо діагоналі взаємно перпендикулярні, то висота дорівнює півсумі основ (середній лінії): h = МК
S-площа h- висота m- середня лінія d1, d2 - довжини діагоналей γ - кут між діагоналями	4.Площа S =  a + b · h 2 S = m · h   S =  d1d2 · sin γ       2
	5. Висота – перпендикуляр (утворює 90° )  Прямокутна трапеція ,тоді АВ=h
R=AO=BO=CO=DO	6.Радіус описаного кола ,як радіус кола описаного навколо трикутника АВD,  ВСD, АСD, АВС
r=OE=OF	7 Радіус вписаного кола r = h/2
	8 Можна вписати коло ,коли суми протилежних сторін рівні   АВ+СD =ВС+АD
	9 Можна описати коло навколо чотирикутника, коли сума протилежних кутів 180° ∠А+∠С=180° ∠В+∠D=180°

Вправи

1. Один з кутів рівнобічної трапеції 60,бічна сторона 18 см, а сума основ 50см. Знайти решта кути трапеції, середню лінію, висоту, діагональ ,периметр та площу трапеції.

 

2. Різниця основ прямокутної трапеції дорівнює 15 см, радіус вписаного кола 4см.Знайти висоту ,периметр , середню лінію площу та діагоналі трапеції.

 

3. У  рівнобічній трапеції діагональ є бісектрисою гострого кута і ділить середню лінію на відрізки 6см та 12 см. Знайти висоту, периметр , площу ,діагоналі та кути трапеції. Чи можна вписати коло у дану трапецію.

 

4. Центр кола ,вписаного в рівнобічну трапецію, віддалений від кінців її бічної сторони на 12см та 16 см. Знайти радіус цього коло , висоту , периметр, середню лінію та площу трапеції.

 

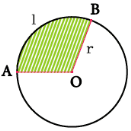
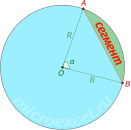
КОЛО та КРУГ

Малюнок і позначення	Формули
	Радіус,діаметр,хорда  Радіус кола R,r - відстань від центра кола О до будь-якої точки  на колі. Діаметр кола D,d - відрізок, який сполучає дві точки кола та проходить через його центр. Хорда кола - відрізок, який сполучає дві точки кола. АВ,СD
	2. Довжина кола,  L = 2πr
Центральний кут – α l-довжина дуги,	3. Довжина дуги кола l = πr/180°∙ α
	4.Площа круга S = πr2
	5. Площа сектора S = πr2  /360° ∙ α
	6.Площа сегмента Від площі сектора відняти площу трикутника АОВ
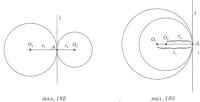
	7 Зовнішній та внутрішній дотики OO=R+r OO=R-r
	8. Вписаний та центральний кути  Вписаний кут дорівнює половині центрального кута, що спирається на ту саму дугу β = α/2
	9 Дотична до кола( відрізки дотичних ,проведені з однієї точки рівні,  дотична перпендикулярна до радіуса ,проведеного в точку дотику)    АВ  ОВ,  АС  ОС AB = AC

 

Вправи

1. Радіус кола на 4см менший за його діаметр. Знайти довжину кола та площу круга, обмеженого цим колом.

 

2. Довжина кола 16П см. Знайти радіус, діаметр,   площу круга, обмеженого цим колом, площу сектора та довжину дуги, що відповідають центральному куту 30°.

 

3. Хорда кола, що стягує дугу 90° ,дорівнює 6см.   Знайти довжину кола та площу круга, обмеженого цим колом. Знайти довжину дуги, площу сектора та площу утвореного сегмента.

 

4. Відстань між центрами двох кіл, що дотикаються зовні дорівнює 30см. Знайти їх  радіуси ,якщо вони відносяться як 2:4. У скільки разів відрізняються їх довжини кіл. Знайти площу круга, обмеженого більшим колом. Знайти площу трикутника вписаного в більше коло та площу квадрата,  ,вписаного в менше коло.

 

 

 

ВИСНОВОК

З метою активізації мислення учнів корисно залучити  їх в процес створення узагальнюючого опорного конспекту. На першому етапі наприклад, запропонувати як домашнє завдання узагальнити матеріал уроку у вигляді невеличкої схеми. Наступний етап: при розв’язуванні завдань з теми, крім запропонованого запитання, знаходимо всі можливі величини даної фігури.

Найбільш вдалі роботи корисно обговорити у класі і використовувати їх згодом при складанні узагальнюючого опорного конспекту.

Використання опорних конспектів на уроках математики дозволяє:

- підвищити пізнавальну діяльність за рахунок раціональності та економічності засвоєння інформації та довготривале збереження в пам'яті;

- покращити якість знань, за рахунок багаторазового повторення;

- при роботі з опорними схемами утворюється значний резерв навчального часу для виконання завдань.

ЛІТЕРАТУРА

1. Амонашвілі Ш.О. «Онови гуманної педагогіки. Як любити дитину», Амріта – 2012
2. Амонашвілі Ш.О. «Чому не прожити нам життя героями духу?», Хмельницький – 2012
3. «Технологія інтенсифікації навчання на основі опорних схем і знакових моделей»

[Електроний ресурс] http://www.kr-suzirya.edukit.dp.ua/metodichna_robota/portfolio_pedagogiv/glushko_v_d/innovacijni_tehnologii/tehnologiya_intensifikacii_navchannya_na_osnovi_opornih_shem_i_znakovih_modelej/

 (Відвідано 25.10.2022)

4. Мерзляк А.Г., Геометрія підручник для 9 класу, Харків «Гімназія» 2017р.
5. Мерзляк А.Г., Геометрія підручник для 8 класу, Харків «Гімназія» 2018р.
6. Роганін О.М., Математика (Навчальний посібник), Київ-Харків «Веста» 2012р.
7. Істер О.С.,  Математика (Збірник тестів), Кам’янець-Подільський «Абетка», 2013р.
8. Сайт – «Геометричні формули»
   [Електроний ресурс] https://formula.kr.ua/trikutniki/vlastivosti-katetiv-median-i-visot-pryamokutnogo-trikutnika.html
   (Відвідано 25.10.2022)
9. Сайт – «Таблиці та формули з математики»
   [Електроний ресурс] https://ua.onlinemschool.com/math/formula/
   (Відвідано 25.10.2022)