Урок "Повторення курсу планіметрії. Урок однієї задачі.".

Приклади методичних розробок. Урок.

 

Тема уроку: Повторення курсу планіметрії. Урок однієї задачі.

Мета уроку:

• повторення основних фактів планіметрії; активізація вмінь і навичок учнів з розв'язування планіметричних задач;
• розвиток аналітичного мислення і системного підходу у вирішенні проблем;
• розвиток пізнавальної активності учнів;
• розвиток обчислювальних навичок учнів;
• виховання культури мовлення і письма, культури математичних обґрунтувань; виховання навичок колективної праці.

Тип уроку: Урок узагальнення і систематизації знань, вмінь і навичок учнів.

Форма організації роботи: урок «мозковий штурм».

Можливі класи і терміни використання:

9 клас:

підсумкове повторення, кінець навчального року;

10 клас:

Тема «Систематизація та узагальнення фактів і методів планіметрії», початок навчального року;

підсумкове повторення, кінець навчального року;

11 клас  – підсумкове повторення, кінець навчального року.

ХІД УРОКУ:

1. Організаційний момент.

Вчитель вітається з учнями, відмічає в журналі відсутніх.

2. Мотивація учнівської діяльності.

Вчитель каже, що в повсякденному житті перед людьми часто виникають проблеми, розв’язання яких вимагає детального підходу і розгляду з різних точок зору. Не завжди ідея, яка приходить першою, є найкращим рішенням. Важливо продумати якомога більше способів розв’язання проблеми.

Крім того, надзвичайно важливим є вміння уважно сприймати інформацію, критично її аналізувати і творчо розвивати.

Саме так можливо знайти оптимальний вихід із ситуації. Або просто красивий. Чи прийнятний для всіх зацікавлених осіб.

3. Постановка завдання.

Вчитель каже, що сьогодні пропонується лише одна задача, яку необхідно розв'язати якомога більшою кількістю способів.

Обов’язковими є умови:

• Прийнятним способом вважається той, який містить реалізовану математичну ідею.
• Учень, користуючись математичним твердженням, обов’язково формулює його в загальному вигляді.

Вчитель оголошує умову задачі:

Периметр рівнобедреного трикутника дорівнює 16 см, а його основа на 1см більша за бічну сторону.

Знайти відстань між радіусами вписаного в трикутник і описаного навколо трикутника кіл.

4. Розв’язування задачі.

Один з учнів зображає на дошці рівнобедрений трикутник, робить відповідні позначення, проводить аналіз даних; встановлює довжини сторін.

На наступному етапі учні пропонують свої ідеї для розв’язання задачі чи її конкретної частини. Якщо ідея прийнятна втілюють її розв’язанням біля дошки.

Прогнозована учнівська ідея 1.

Нехай на малюнку зображено трикутник АВС, в якому АВ = ВС = 5см, АС = 6см. Н - точка основи. ВН АС. Тоді НА = НС = Зсм (за властивістю висоти рівнобедреного трикутника).

Оскільки трикутник ВНС - єгипетський, то ВН = 4см.

Або з теореми Піфагора ВН = = 4 см.

Нехай точка О - центр вписаного в трикутник АВС кола. Тоді О є ВН, оскільки центр вписаного кола є точкою перетину бісектрис, а ВН – бісектриса (за властивістю висоти рівнобедреного трикутника), проведена до основи АС.

Опустимо з точки О перпендикуляр на сторону ВС. Нехай його основа - точка К, тобто, ОК ⊥ ВС. Тоді ОК = ОН як радіуси .вписаного кола.

Трикутники ВОК та ВСН – подібні як прямокутні з гострим кутом В. Тоді   = .                   

  Тобто,   = звідки радіус вписаного кола ОН дорівнює 1,5 см.

Вчитель. А чи можна по - іншому знайти радіус вписаного кола?

Прогнозована учнівська ідея 2.

Маємо, що НС = КС = З см за властивістю дотичних, проведених до кола з однієї точки. Тоді ВК = 2см. І з вищевказаної подібності маємо інше співвідношення:

= , тобто, = , звідки радіус вписаного кола ОН дорівнює 1,5 см

Вчитель. Як ще можна було шукати радіус вписаного кола?

Прогнозована учнівська ідея 3.

З трикутника ВНС маємо, що tg∠B = = .

З трикутника ВКО маємо, що tg∠B = = . Прирівнявши їх, одержимо: ОК = r = 1,5см.

Вчитель. Як ще можна було шукати радіус вписаного кола?

Прогнозована учнівська ідея 4.

Застосуємо метод площ. Знаючи, що S = рг, і маючи р = 8см, порахуємо площу трикутника ABC. S_АВС = 0,5ВН АС = 12 см². Тоді г = 1,5см.

Аналогічно, скориставшись формулою R = , де a,b,c одержимо, що R = (см). Тоді відстань між центрами описаного і вписаного кола: НО = HO =   = (cм).

Вчитель. А чи можна по - іншому знайти площу трикутника ABC?

Прогнозована учнівська ідея 5.

Скористаємось  формулою Герона для обчислення площі трикутника :

S = , а, в, с – сторони трикутника. Для трикутника АВС маємо, що   р = 8 см, отже: S  = = 12 см² .

Вчитель. Як ще можна було шукати площу трикутника ABC?

Прогнозована учнівська ідея 6.

З трикутника ВНС sin ∠ НВС = . Знайдемо sin 2 ∠ НВС = 2 sin ∠ НBC cos ∠HBC.

сos ∠HBC= . Тоді sin 2 ∠ НВС = . S = 0,5АВ ВС sin 2 ∠ НВС = 12см².

Вчитель. А чи можна по - іншому знайти sin 2∠НВС?

Прогнозована учнівська ідея 7.

З трикутника ABC за теоремою косинусів знайдемо косинус кута ABC. Тоді за основною тригонометричною тотожністю - синус цього кута.

Вчитель. Як ще можна було шукати радіус вписаного кола?

Прогнозована учнівська ідея 8.

Нехай Р точка перетину вписаного кола з висотою ВН (Р міститься між точками О і В). ОН = ОР = г. Тоді за властивістю січної і дотичної, проведених до кола з однієї точки, маємо, що BP ВН = ВК². Тут ВР = ВН 2г = 4 2r, ВК = 2см, звідки г = 1,5см.

Вчитель. Давайте тепер кількома різними способами знайдемо радіус описаного кола.

Прогнозована учнівська ідея 9.

Нехай точка F центр описаного навколо трикутника ABC кола. Тоді дана точка лежить на прямій ВН, оскільки центр описаного кола лежить на перетині серединних перпендикулярів до сторін трикутника, а НВ – серединний перпендикуляр до основи АС. Отже, FB = FA = R. Опустимо перпендикуляр з точки F на сторону АВ. Його основа - точка М. FM ⊥ АВ. AM = ВМ за властивістю висоти рівнобедреного трикутника, оскільки трикутник АВF – рівнобедрений за означенням (FB = FA = R). Тоді AM = ВМ = 2,5см.

З подібності трикутників АВН і FВМ (як прямокутних зі спільним кутом В) одержимо, що FВ = R =   = см.

Вчитель. Як ще можна було шукати радіус описаного кола?

Прогнозована учнівська ідея 10.

Скористаємося наслідком з теореми синусів для трикутника АВС. Знаючи з попереднього, що АВС = , маємо, що відношення довжини сторони АС до синуса протилежного кута - це і є радіус описаного кола: R = 3   см.

Вчитель. Як ще можна було шукати відстань між центрами вписаного і описаного кола?

Прогнозована учнівська ідея 11.

Скориставшись формулою Ейлера для знаходження відстані d між центрами вписаного і описаного кола, маємо:

d = = = (cм).

 

Орієнтовний малюнок до задачі:

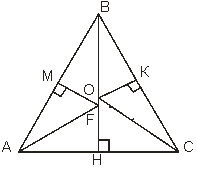
Вчитель. Чи можна було на якомусь з етапів розв’язання зробити щось по – іншому?

Прогнозована учнівська ідея 12.

Можна було скористатися методом подвоєння медіани при знаходженні висоти (бісектриси, медіани) ВН, проведеної до основи АС. Для цього відкласти на прямій ВН відрізок НN так, щоб точка Н була серединою відрізка ВN. Тоді АВСN – паралелограм за ознакою (його діагоналі точкою перетину діляться навпіл). Тоді скористаємося формулою: =2(яка пов’язує сторони і діагоналі паралелограма. Звідки знайдемо діагональ ВN, половиною якої є висота ВН.

Вчитель. Як по - іншому можна було шукати висоту (бісектрису, медіану) ВН?

Прогнозована учнівська ідея 13.

Можна було скористатися формулою для обчислення медіани трикутника:

= b і c бічні сторони АВ і ВС, а = АС.

Вчитель. Як принципово по - іншому можна розв’язати цю задачу?

Прогнозована учнівська ідея 14.

Розв'яжемо дану задачу за допомогою методу координат .

Помістимо трикутник АВС в декартову систему координат так, щоб вісь ординат співпадала з прямою ВН, точка В належала її додатній півосі, а початком системи координат була точка Н. Тоді: Н (0;0), В (0;4), А (–3;0), С (3;0).

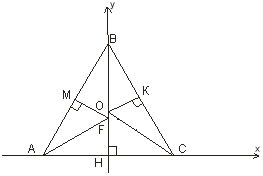
Знайдемо координати точки F. Оскільки вона належить прямій ВН, то F(0;у_F). Вона рівновіддалена від точок А(–3; 0) і В(0; 4), тобто, виконується умова А F = В F. Скориставшись

формулою відстані між двома точками в координатах і тим, що AF² = BF², маємо:

(3)² + (у_F)²  = (y_F – 4)² ; 9 + = 16 – 8y_F + , звідки 8y_F = 7; F (0; ) .

Тоді радіус описаного кола R = BF = 3.

Вчитель. Як ще можна було шукати координати точки F?

Прогнозована учнівська ідея 15.

Точка F – точка перетину серединного перпендикуляра до сторони АВ та прямої ВН.

Нехай точка М – середина сторони АВ, де А(–3; 0), В(0; 4). Знайдемо координати точки М(х_М ; у_М ) за формулами координат середини відрізка:

х_М = = – ;     у_М = = 2. Тобто, М(– ; 2) .

Знайдемо кутовий коефіцієнт k_AB прямої АВ:

k_AB = tg = .

Тоді кутовий коефіцієнт k прямої – серединного перпендикуляра до відрізка АВ:

k = – , оскільки добуток кутових коефіцієнтів двох взаємно перпендикулярних прямих –1. Знайдемо її рівняння, скориставшись рівнянням прямої із заданим кутовим коефіцієнтом (k = – ¾), яка проходить через задану точку (точка М(– 3/2; 2)):

у = – (х + ) + 2 = – х – + = – х + .

Рівняння прямої ВН: х = 0.

Розв’язавши систему 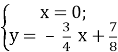,     одержимо координати точки F: F(0; ) .

 

Знайдемо координати точки О.

Оскільки вона належить прямій ВН, то О(0;у_о).

З за властивістю бісектриси бісектриса СО ділить відрізок ВН у відношенні:

  = = . Далі можна скористатися формулами для визначення координат точки, яка ділить даний відрізок у відношенні k:

у_о =   = =1 . Тобто, О(0; 1) . Тоді радіус вписаного кола r = HO = 1

Отже, знову скориставшись формулою відстані між двома точками в координатах, маємо: R – r = FO = =

Вчитель. А чи можна по - іншому знайти координати точки О?

Прогнозована учнівська ідея 16.

Можна знайти координати точки О(0;у_о) як координати точки, рівновіддаленої від точок Н(0; 0) і К(х_к ; у_к).

Точка К належить прямій ВС. Рівняння прямої ВС знайдемо як рівняння прямої, яка проходить через дві точки В(0; 4) і С(3; 0).

  = ;        – 4х = 3у – 12;        3у = – 4х + 12;

Отже, рівняння прямої ВС:  у = – х + 4. Тоді К(х_к ; – х_к + 4).

З властивості дотичних, проведених до кола з однієї точки, маємо: НС = КС = 3. Скориставшись формулою відстані між двома точками в координатах і тим, що

КС² = 9, одержимо:

(3 – х_К)² + (0 + х_К – 4)² = 9;

9 – 6х_К + +

– = 0;

25 – 150 + 144 = 0.

Знайдемо дискримінант даного рівняння:

D = – 4

За формулою коренів квадратного рівняння:

х_К =  = ;

х_К =     або   х_К = .

– ні, тому К ( ; ) .

Скориставшись формулою відстані між двома точками в координатах і тим, що точка О рівновіддалена від точок Н і К, тобто, ОН² = ОК², маємо:

 

 

2х_о = 3;

х_о = 1 , тобто, О (0; 1) .

Тоді відстань між центрами вписаного і описаного кіл  см (якщо прийняти 1 см за одиницю в обраній системі координат).

Відповідь: відстань між радіусами вписаного в трикутник і описаного навколо трикутника кіл  см.

5. Підведення підсумків уроку.

Вчитель підсумовує зроблене, ставить запитання учням про оцінку ефективності їх діяльності на уроці, а також діяльності класу в цілому. Виставляє оцінки, мотивуючи.

Вчитель ставить завдання додому:

• базуючись на зроблених впродовж уроку записах, повторити основні твердження, використовувані під час розв'язання задачі;
• повторити наступний (перераховується вчителем) матеріал (теоретичний матеріал, що не був використаний під час розв'язання задачі, але який необхідний для продовження успішної роботи з теми «Повторення»);
• реалізувати з повним письмовим поясненням ідеї… (вказуються ідеї, що прозвучали на уроці, але не були реалізовані за браком часу) або ідеї, які учні не встигли озвучити.