Міністерство освіти і науки України

Запорізький електротехнічний фаховий коледж

Національного університету «Запорізька політехніка»

 

 

 

 

 

 

 

 

 

 

 

ТЕХНІЧНА МЕХАНІКА

 

 

Блок 1 «Теоретична механіка» Збірник опорних конспектів лекцій для всіх технічних  спеціальностей 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Викладач                                                                                І.В. Дубовський

 

 

 

 

 

 

 

 

2020   ВСТУП................................................................................................... 3

1.ТЕОРЕТИЧНА МЕХАНІКА.ЗАГАЛЬНІ ПОНЯТТЯ....................................... 4

2 ОСНОВНІ ПОНЯТТЯ СТАТИКИ................................................................... 6

2.1 СИЛА - ЦЕ МІРА МЕХАНІЧНОЇ ВЗАЄМОДІЇ ТІЛ..................................... 7

2.2 АКСІОМИ СТАТИКИ................................................................................. 10

2.3 ЗВ'ЯЗКИ І РЕАКЦІЇ ЗВ'ЯЗКІВ.................................................................... 14

2.4 КОРОТКІ ВІДОМОСТІ ПРО ВАЖЕЛІ....................................................... 17

2.5  ПОНЯТТЯ ПРО БАЛКИ, ОПОРИ І РЕАКЦІЇ ОПОР БАЛОК................... 18

3 ЦЕНТР ВАГИ................................................................................................. 21

3 ОСНОВНІ ВІДОМОСТІ ПРО ТЕРТЯ............................................................ 25

4 КІНЕМАТИКА............................................................................................... 34

4.1 ОСНОВНІ ПОНЯТТЯ КІНЕМАТИКИ....................................................... 34

4.2 ОБЕРТАЛЬНИЙ РУХ  ТВЕРДОГО ТІЛА НАВКОЛО НЕРУХОМОЇ ВІСІ 41

4.3 СПОСОБИ ПЕРЕДАЧІ ОБЕРТАЛЬНОГО РУХУ....................................... 44

5 ДИНАМІКА................................................................................................... 48

5.1 АКСИОМИ ДИНАМІКИ............................................................................ 48

5.2  РОБОТА ТА ПОТУЖНІСТЬ...................................................................... 51

5.3 КОЕФІЦІЄНТ КОРИСНОЇ ДІЇ.................................................................... 54

5.4 ФАКТОРИ ЯКІ ВПЛИВАЮТЬ НА КОЕФІЦІЄНТ КОРИСНОЇ ДІЇ........... 56

5.5 СИЛИ ІНЕРЦІЇ............................................................................................ 58

 

ЗМІСТ

ВСТУП

 

Теоретична механіка

Вступ: короткі відомості про предмет і його розділи.

Технічна механіка - це інженерна наука, яка складається із трьох окремих, але взаємно пов'язаних предметів: теоретичної механіки, опору матеріалів і деталей механізмів і машин.

Технічна механіка - це прикладна наука, бо її знання мають застосування в різних галузях техніки і промисловості: машинобудуванні, будівництві, літакобудуванні, космонавтиці і таке інше.

Знання однієї частини предмету є підґрунтям для засвоєння іншої, тому вони вивчаються завжди у такій послідовності:

Теоретична механіка - це частина, яка вивчає закони механічного руху тіл і особливості різних рухів, рівновагу твердих тіл (різних матеріальних об'єктів), взаємодію твердих тіл.

Опір матеріалів - це частина, яка вивчає методи розрахунків деталей машин, приладів, споруд та елементів конструкцій на міцність, жорсткість, стійкість, витривалість.

Деталі механізмів і машин - це частина, яка вивчає склад, принцип дії, основи розрахунків і конструювання найбільш поширених механізмів, з'єднань, деталей і вузлів загального призначення.

Вивчення технічної механіки ґрунтується на знаннях предметів - математика, фізика, креслення, технологія конструкційних матеріалів, основи стандартизації.

Механіка - одна з найдавніших наук,   вона виникла ще у V столітті до нової ери у Греції. Усім відомі імена вчених-механіків: Арістотель, Архімед, Леонардо да Вінчі, Галілей, Ньютон, Гук, Ейлер, Мор, Даламбер, Кулон, Вьолер, Жуковський, Мещерський, Чаплигін, Ціолковський. Вершиною механіки разом з іншими науками є польоти літаків та космічних кораблів, переміщення океанських суден та підводних човнів.

 

            

 

Перший розділ технічної механіки має назву "Теоретична механіка" і складається з трьох частин: кінематика, статика, динаміка.

 

1.ТЕОРЕТИЧНА МЕХАНІКА. ОСНОВНІ ПОНЯТТЯ

 

1.                       Механічний рух - це зміна положення різних предметів у прос торі і часі відносно інших, умовно нерухомих матеріальних тіл.

Взагалі матерія, рух, час і простір - це найбільш узагальнені філософські поняття. Наприклад: рух - це і механічне переміщення предметів, і розвиток суспільства, і будь-яка зміна, і мислення.

Найбільш простий рух - механічний, бо його можливо спостерігати неозброєним оком. Вчені почали вивчати його давно, ще у IV віці до н.е.

 

2.                       Окремим випадком руху є так звана рівновага, тобто стан спокою, нерухомості, коли немає переміщення одного тіла відносно другого. Цей випадок вивчається у розділі "Статика".

 

3.                       Абсолютно тверде тіло - це будь-який предмет, що не змінює своєї форми і розмірів при взаємодії з другими тілами, або це тіла, що не деформуються. Таких тіл у природі не існує, але це умовне поняття введено для спрощення при вирішення задач у теоретичній механіці і буде анульоване у опорі матеріалів, де вивчається поведінка реальних тіл, що деформуються під дією зовнішніх сил.

 

4.                       Матеріальна точка - так називають абсолютно тверде тіло, якщо формою і розмірами цього тіла можливо знехтувати у даній задачі. Це допустимо у двох випадках:

 

 

        

4.1.                       Коли розміри одного тіла занадто малі у порівнянні з іншими тілами в задачі: наприклад, штучний супутник Землі у порівнянні з Землею або відстанню до Сонця дуже малий, тому на космічних картах його зображують матеріальною точкою.

 

 

 

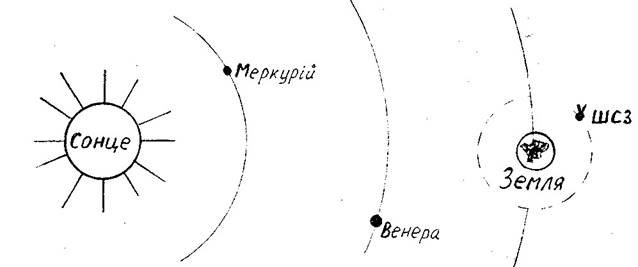
Відстань від Сонця до Землі 150 млн. км, тобто S = 150x106 км; діаметр Землі d₃ = 12740 км. Висота орбіти штучного супутника Землі від 970 до 35800 км над Землею.

Хоча сам ШСЗ - це дуже складний виріб, який складається з багатьох деталей, але так простіше спостерігати його політ і робити розрахунки цього польоту у комічному просторі.

4.2.                       Коли всі точки твердого тіла рухаються тільки поступально, відстань між ними не змінюється: поршень у ДВЗ, спортивний спис, корпус машини.

Закони механічного руху твердих тіл вивчаються у розділі "Кінематика". "Кінема" - грецьке слово, означає рух - його запропонував стародавній вчений Арістотель, який вивчав рух як філософ і механік ще у IV столітті до нової ери. Арістотель був вихователем і наставником великого полководця Олександра

Македонського.

        

2 ОСНОВНІ ПОНЯТТЯ СТАТИКИ

СТАТИКА - це розділ теоретичної механіки, у якому вивчаються умови, за яких тіло перебуває у рівновазі, тобто у спокої або рухається прямолінійно і рівномірно.

ОСНОВНІ ПОНЯТТЯ СТАТИКИ

1.                       АБСОЛЮТНО ТВЕРДЕ ТІЛО (АТТ) - це матеріальне або фізичне тіло (будь-який предмет, деталь), розміри і форми якого не змінюються під дією зовнішніх сил, тобто це тіло, що не деформується. І хоч абсолютно твердих тіл у природі не існує, це умовне поняття застосовується у теоретичній механіці для спрощення формул і задач.

А реальні тіла, які деформуються, вивчаються у розділі "ОПІР МАТЕРІАЛІВ".

Зображення АТТ:

 

2.                       МАТЕРІАЛЬНА ТОЧКА (МТ) - це точка, що має масу, або це тіло, розмірами і формою якого у даній задачі можна знехтувати. Цю заміну АТТ на МТ можна робити у двох випадках:

2.1.                       Коли розміри основного тіла у задачі дуже малі у порівнянні з іншими розмірами: подивіться у небо вночі: дуже великі зірки ми бачимо у вигляді блискучих точок, бо вони від нас дуже далеко.

2.2.                       Коли АТТ рухається поступально, і відстань між усіма точками не змінюється.

Виключення: АТТ, яке обертається, не можна замінювати матеріальною точкою.

3.                       СИЛА - це механічна величина, що виникає при взаємодії тіл. Результатом взаємодії тіл є зміна стану тіла - воно починає рухатись або зупиняється, або деформується.

        

2.1 СИЛА - ЦЕ МІРА МЕХАНІЧНОЇ ВЗАЄМОДІЇ ТІЛ

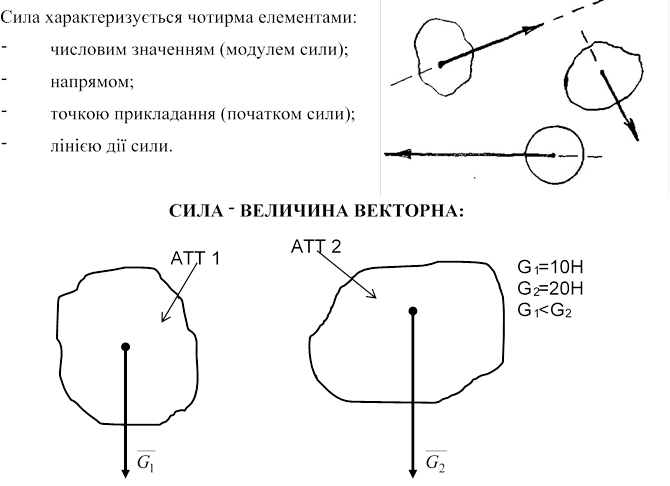
Тіла виготовлені із одного матеріалу із однаковою питомою вагою.

У МЕХАНІЦІ ВИВЧАЮТЬСЯ ТАКІ СИЛИ:

-                   сила тяжіння:

-                   сила тертя;

-                   сила тиску;

-                   реактивні сили (реакції зв’язків);

-                   сили пружності (вивчаються у опорі матеріалів).

Сили у механіці позначають такими буквами: G, F, R, N, S, Q, Т, X, Y. 

 

4.                    СИСТЕМА СИЛ - це сукупність кількох сил, що одночасно діють на якесь АТТ.

Системи поділяються залежно від їх розташування так:

-                   просторові або плоскі;

-                   збіжні або довільно розташовані;

-                   паралельні у просторі або площині.

За цими ознаками у теоретичній механіці вивчають шість систем сил: вільне тіло має шість ступенів вільного руху - три поступальних і три обертальних відносно осей Х, Y, Z.

4.1.     Приклад плоскої системи збіжних сил:

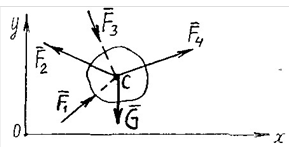Усі сили такої системи розташовані у площині       ХОY і лінії дії усіх сил перетинаються у одній точці С.

 

4.2.     Приклад плоскої системи довільно розміщених сил:

 

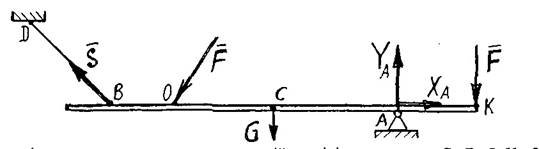
Сили цієї системи не перетинаються у одній точці, і вектори сил G, F, S, X_A, Y_A не паралельні. З такими системами сил більш усього пов’язані задачі у розділі "СТАТИКА".

5.                    ЕКВІВАЛЕНТНІ СИСТЕМИ СИЛ — це різні системи сил, які створюють однакову дію на тіло. Це твердження дає змогу складну систему сил замінити більш простою при розв’язуванні задач. Еквівалентні - значить рівнозначні, однакові.

        

6.                    РІВНОДІЮЧА СИЛА R — це одна сила, еквівалентна системі сил.

R F₁ F₂ - цей вираз має назву ГЕОМЕТРИЧНА СУМА ДВОХ СИЛ F₁ і F ₂

: матеріальна точка А буде рухатись у напрямі сили R .

За абсолютним значенням R  F₁ F₂, тобто модуль R менше арифметичної суми сил ^F₁ і ^F₂ .

Яскравий приклад: човен, який пливе за течією, а в його вітрила дме вітер під кутом φ до течії - човен пливе під кутом α відносно берегів.

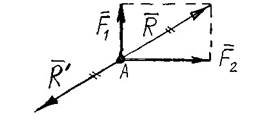
7.                    ЗРІВНОВАЖУВАЛЬНА СИЛА R^- це сила, яка дорівнює рівнодіючій

R за модулем і має напрям, протилежний їй. Сума сил R^ і R дорівнює нулю, тобто під дією таких двох сил тіло не буде рухатись: якщо до човна прикласти силу R - він зупиниться.

 

 

 

R  R  0

- цей вираз відображає математично стан спокою АТТ - тобто його рівновагу.

2.2 АКСІОМИ СТАТИКИ

АКСІОМАМИ називають положення, які приймають без доведень, бо ці положення завжди підтверджуються дослідами.

Аксіоми статики встановлюють основні властивості сил і систем сил, які прикладені до абсолютно твердих тіл.

Аксіоми статики сформулювали видатні вчені-механіки І.НЬЮТОН і Г.ГАЛІЛЕЙ - у XVII і XVIII століттях.

АКСІОМА I – принцип інерції Галілея або перший закон НЬЮТОНА:

БУДЬ-ЯКЕ ТІЛО ЗБЕРІГАЄ СТАН СПОКОЮ АБО ПРЯМОЛІНІЙНОГО РІВНОМІРНОГО РУХУ, ПОКИ ЯКІСЬ СИЛИ НЕ ВИВЕДУТЬ ТІЛО ІЗ ЦЬОГО СТАНУ.

Інерція або інертність - одна із основних властивостей матерії: це здатність тіла зберігати стан, у якому воно знаходиться.

АКСІОМА II - умова рівноваги двох сил:

ТІЛО ПЕРЕБУВАЄ У СТАНІ СПОКОЮ, ЯКЩО НА НЬОГО ДІЮТЬ ДВІ СИЛИ, РІВНІ ЗА МОДУЛЕМ І ПО ОДНІЙ ПРЯМІЙ У ПРОТИЛЕЖНИХ НАПРЯМАХ.

	F1 F 2  0

 

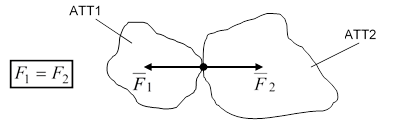
АКСІОМА III - аксіома взаємодії, або третій закон НЬЮТОНА:

СИЛИ ВЗАЄМОДІЇ ДВОХ ТІЛ ЗАВЖДИ ОДНАКОВІ ЗА МОДУЛЕМ І ПРОТИЛЕЖНО СПРЯМОВАНІ ПО ОДНІЙ ПРЯМІЙ.

Це значить, що однобічної дії одного тіла на друге не буває, тобто усі сили природи - парні сили:

        

АКСІОМА IV - РІВНОВАГА ТІЛА НЕ ПОРУШИТЬСЯ, ЯКЩО ДО НЬОГО ПРИКЛАСТИ АБО ВІДНЯТИ ВІД НЬОГО ЗРІВНОВАЖЕНУ СИСТЕМУ СИЛ:

 

 

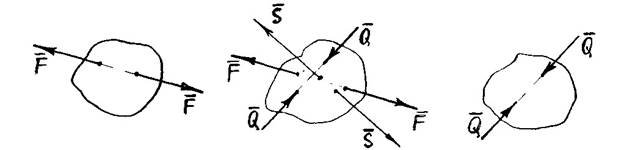
ВИСНОВОК із III і IV АКСІОМ:

Механічний стан твердого тіла не порушиться, якщо силу перенести вздовж лінії її дії у будь-яку точку тіла.

Доведення: маємо АТТ, на яке діє сила F в точці А по лінії AB.

Завдання: треба перенести силу F в точку В, не змінюючи рівновагу тіла. Відповідно до IV АКСІОМИ можна прикласти у точці В дві сили: F₁ і F₂, які за модулем рівні силі F.

 

 

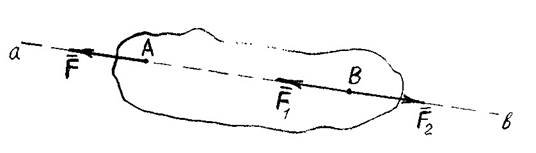
Розглянемо ці сили так: F₁ і F₂ рівні і протилежні можна відкинути відповідно IV аксіомі на основі III аксіоми, а сила F₁=F, рівновага тіла не змінилась, хоч тепер сила знаходиться у точці В.

Тобто сила - це вектор, який можна переносити, якщо вона прикладена до АТТ.

Силу, прикладену до реального тіла, що деформується, переносити не можна.

        

АКСІОМА V- правило паралелограма:

РІВНОДІЮЧА ДВОХ СИЛ, ПРИКЛАДЕНИХ ДО ТІЛА У ОДНІЙ ТОЧЦІ,

ДОРІВНЮЄ      ЗА      МОДУЛЕМ          ДІАГОНАЛІ         ПАРАЛЕЛОГРАМА, ПОБУДОВАНОГО НА ДАНИХ СИЛАХ, ЗБІГАЄТЬСЯ З ДІАГОНАЛЛЮ І ПРИКЛАДЕНА У ТІЙ САМІЙ ТОЧЦІ.

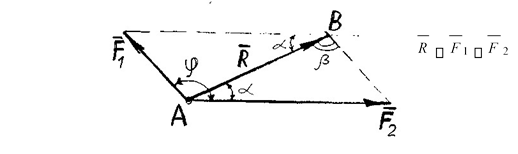
Замість паралелограма можна побудувати трикутники сил, послідовність додавання на результат не впливає:

 

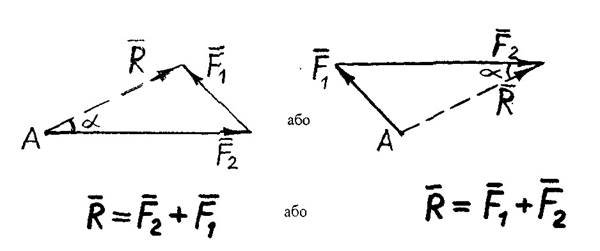
 Модуль і напрям сили R можна обчислити аналітично, тобто за формулами.

       За теоремою косинусів:        R²  ^F₁²  ^F₂²  2  ^F₁  ^F₂ cos(180 ^o ) , або                     ^R2  F₁²  F₂²  2  F₁  F₂ cos_.

Звідки                       R  F₁²  F₂²  2  F₁  F₂  cos_ .

                                                                                        F^{1                          R                      R} ,

            За теоремою синусів:                                      

                                                                                          sin  sin(180 ^o )          sin 

Звідки напрям R:                 sin   F₁  sin ^

R

                                           arcsin F^{1 sin }.

R

        

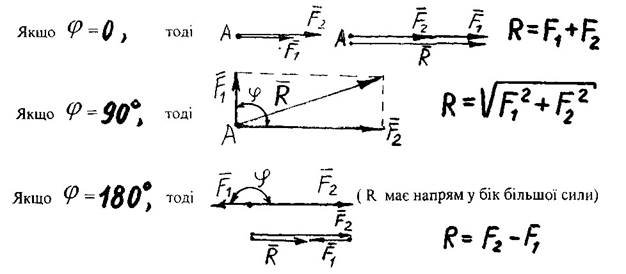
            Окремі випадки:

 

 

2.3 ЗВ'ЯЗКИ І РЕАКЦІЇ ЗВ'ЯЗКІВ

У механіці тіла (деталі, предмети) поділяють на вільні і невільні. Невільними називають тіла, переміщення яких обмежено у просторі хоча б у одному напрямі другими тілами.

Зв’язками називають тіла, які обмежують рух основного тіла.

Приклади зв’язків: підлога, стіна, трос, канат, мотузка, дріт, будь-яка поверхня, жорсткі стержні, колони, підшипники, підп’ятники, різні шарніри і таке інше.

На основі III закону НЬЮТОНА між двома тілами при взаємодії виникають сили дії і протидії, які рівні за величиною і протилежні за напрямом.

Сили   протидії з  боку   зв’язків  називаються   реактивними   силами,   або РЕАКЦІЯМИ.

Активні сили намагаються переміщувати тіло, до якого вони прикладені. Це сили тяги, сили тяжіння, сили електричної взаємодії, сили тиску вітру, води або інше зовнішнє навантаження.

Для визначення реактивних сил (або реакцій) треба застосовувати принцип звільнюваності: усяке невільне тіло можна розглядати як вільне, якщо відкинути зв’язки і замінити їх реакціями - тіло буде перебувати під дією системи активних і реактивних сил.

Загальне правило: напрям реакції зв’язку завжди протилежний дії активних сил на даний зв’язок.

Реакції зв’язків завжди невідомі в задачах механіки. При вирішенні задач спочатку треба знайти їх напрям - залежно від виду зв’язку, а потім обчислити їх величину. Для цього існують різні методи визначення реакцій для кожної системи сил.

У конструкціях трапляються різні зв’язки, які можна за деякими подібними ознаками об’єднати у групи. За кількістю реакцій і своєю конструкцією зв’язки можна поділити на прості і складні. Розглянемо приклади простих зв’язків і реакцій в них.

        

1. ІДЕАЛЬНО ГЛАДЕНЬКА ПЛОЩИНА АБО ПОВЕРХНЯ

(без урахування тертя).

 

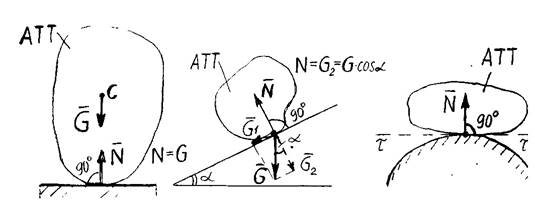
G - активна сила; N - дорівнює силі тиску тіла на поверхню або на площину. Реакція N таких площин і поверхонь завжди перпендикулярна (тобто нормальна) до площини або до дотичної τ τ. N - нормальна реакція площини.

2.                       ГНУЧКІ ЗВ`ЯЗКИ - це ланцюги, канати, мотузки, нитки, троси, проводи, дроти.

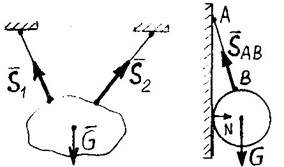Особливість гнучких зв’язків: під вантажем вони тільки розтягуються (стискатись не можуть). Реакції гнучких зв’язків завжди напрямлені вздовж зв’язків від тіла. S₁, S₂, S_АВ - це і є реакції гнучких зв’язків.

 

3.                       ЖОРСТКІ СТЕРЖНІ - це довгі тонкі елементи конструкцій із дерева,

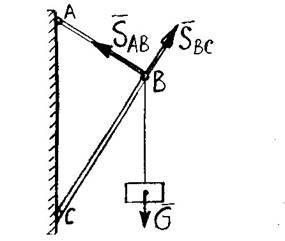металу, залізобетону Кінці їх закріплені шарнірно. Реакції прямих стержнів завжди напрямлені вздовж стержнів. Жорсткі стержні під вантажем можуть і стискатись, і розтягуватись: під дією сили тяжіння вантажу стержень АВ розтягується, стержень ВС - стискається.

Конструкція із двох стержнів називається кронштейном.

S_АВ і S_ВС - це і є реакції стержнів.

        

При вирішенні задач статики треба знати спочатку напрям реакцій зв’язків, а потім визначити їх величину.

Якщо у задачі лінії дій активних сил і реакцій зв’язків перетинаються у одній точці, то така система сил називається плоскою системою збіжних сил. Існує три способи визначення невідомих реакцій для такої системи сил:

 

1.                       Аналітичний - треба скласти відповідні рівняння рівноваги і розв’язати їх відносно невідомих реакцій. Це є найбільш загальний спосіб для всіх задач механіки. Наприклад: ΣF_ix=0; ΣF_iy=0.

 

2.                       Графічний - треба зобразити у масштабі замкнений многокутник сил, сторони якого відповідно паралельні векторам заданих активних сил і реакцій зв’язків. Значення невідомих реакцій знаходяться шляхом вимірювання у тому ж масштабі сторін многокутника, відповідних реакцій зв’язків.

 

3.                       Геометричний - якщо у задачі одна активна сила і дві невідомі реакції, то многокутник буде трикутником, до якого можна застосувати будь-яку формулу з математики: теорему синусів, косинусів, Піфагора або тригонометричні функції (залежно від форми трикутника), і визначити таким чином невідомі реакції як сторони трикутника.

 

При вирішенні задач різними способами відповіді реакцій повинні співпадати.

 

Приклади застосування різних способів визначення реакцій зв’язків будуть розглядатись досконало на практичних заняттях.

 

2.4 КОРОТКІ ВІДОМОСТІ ПРО ВАЖЕЛІ

   ВАЖІЛЬ – це довгий тонкий брус або стержень, який має вісь обертання. Залежно від того, як розташовані сили відносно осі, важелі умовно поділяють на важелі I роду – якщо сили з обох боків, і важелі II роду – якщо сили з одного боку.

       Важелі застосовують з давніх здавен для збільшення даної сили: катапульти, весла у човні, важільні терези, важільні підсилювачі у верстатах для затиснення заготівок і таке інше.

       За допомогою не рівноплечого важеля можна збільшити дану силу (силу людини) в багато разів. „Дайте мені силу опори – і я підніму Землю” – так сказав великий механік Архімед про можливості не рівноплечого важеля.          УМОВА РІВНОВАГИ УСІХ ВАЖЕЛІВ – це рівність нулю

алгебраїчної суми моментів усіх сил, прикладених до нього, відносно осі обертання – точки О.

 

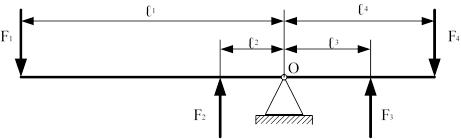
 F₁ l₁  F₂ l ₂  F₃l₃  F₄l ₄  0           або         M _O (F_i )  0 .

 

 

2.5  ПОНЯТТЯ ПРО БАЛКИ, ОПОРИ І РЕАКЦІЇ ОПОР БАЛОК

 

 Балкою у механіці називають розрахункову схему усіх довгих і тонких деталей, закріплених на спеціальних опорах і утримуючих згин під дією зовнішніх сил. Опори балок за їх будовою можна розподілити на три основних типи:

1.шарнірно-рухома опора; 2. шарнірно-нерухома опора;

3. жорстке затиснення.

 В опорах виникають реактивні сили, які в задачах статики завжди невідомі. Кожна опора має особливості.

1.           Шарнірно-рухома опора допускає поворот навколо осі шарніра і лінійне переміщення паралельно опорній площині (на рисунку 1 – опора позначена А). Реакція такої опори має напрям, перпендикулярний до опорної площини.

2.           Шарнірно-нерухома опора допускає поворот навколо осі шарніра і не допускає ніяких лінійних переміщень. Реакція такої опори має напрям, перпендикулярний до осі шарніра; модуль і напрям такої реакції завчасно невідомі. При вирішені задач таку реакцію розкладають на дві взаємно перпендикулярні складові - невідомі за числовим значенням, але відомі за напрямом (на рисунку 1 опора позначена В).

 

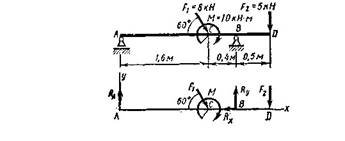
Рисунок 1 - Шарнірні опори балки і реакції в них

 На рисунку позначена балка АD. Зображена опора А - шарнірно-рухома, реакція в ній R_А (або Y_А).

       Опора В — шарнірно-нерухома, реакції в ній R_BX і R_BY (або Х_В, Y_B )■    Реакції опор викликані зовнішніми силами і моментом:

F₁=8кн, F₂=5кн, М=10кн·м.

        

 Невідомі реакції визначають після рішення відповідної системи рівнянь рівноваги:

-              якщо до балки прикладена хоча б одна похила сила (F₁), складають основну (або першу) групу рівнянь рівноваги:

                                                 Σ F_ix=0

                                                 Σ F_iy=0

                                                 Σ M_A(F_i)=0

-              якщо всі сили вертикальні, то реакція R_BX (або Х_В) дорівнює нулю, застосовують другу групу рівнянь:

                                                 Σ M_A(F_i)=0

                                                 Σ M_B(F_i)=0

                                                 Σ F_iy=0

                             де рівняння Σ F_iy=0 застосовується як перевірне (приклади будуть

на практичному занятті).

3.           Якщо балка закріплена одним кінцем, вона називається консольною. Кріплення такої балки - жорстке затиснення - не допускає ні лінійних переміщень, ні поворотів закріпленого кінця балки. Жорстке затиснення замінюють реактивною силою (у точці А) - R_А , невідомою за напрямом, тому її зображують розкладеною на дві складові R_X та R_Y , і реактивним моментом М_R (із точки А).

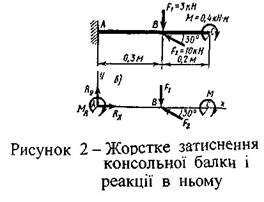На рисунку 2 показана балка АС. Зовнішнє навантаження: Сили F₁=3кн; F₂=10кн; M=0,4кнм.

Реакції у точці А: R_Ау, R_Ах, МR.

Для визначення реакцій треба скласти 1 або 2 системи рівнянь рівноваги для заданої балки, визначити числові значення реакцій. Якщо при розв'язанні задачі будь-яка реактивна сила або реактивний момент виявляться від’ємними, то їх дійсний напрям протилежний зображеному на рисунку.

        

Приклади визначення реакцій будуть розглянуті на практичному занятті і в розрахунково-графічній роботі.

       Різниця між рисунком до задачі і розрахунковою схемою сил до неї показана на рисунку 3.

Умова до задачі:

 

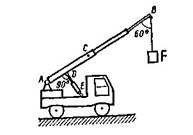
Рисунок 3 - Порівняння рисунку до задачі з розрахунковою системою сил до неї.

 

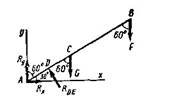
Розрахункова схема сил: заданих зовнішніх F і G і невідомих реакцій зв'язків R_X, R_Y і R_DЕ.

3 ЦЕНТР ВАГИ

 ЦЕНТРОМ ВАГИ називають єдину точку у будь-якому тілі, яка є центром його рівноваги: якщо тіло підвісити за цю точку або обперти на неї, воно буде знаходитись у горизонтальному положенні і не перекидатись.  Центр ваги позначають буквою С. У точці С прикладена сила тяжіння G, з якою тіло притягується до Землі.

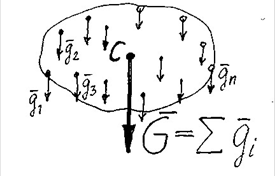
Сила G є рівнодіючою по відношенню до

елементарних сил тяжіння g _i всіх частин тіла, які утворюють просторову систему паралельних сил (рисунок 1).

Рисунок 1.

 Центр ваги тіла, складної пластини або складного перерізу можна визначити двома способами: практичним і аналітичним. Практичний спосіб полягає у тому, що центр ваги легко визначити, якщо два або три рази підвисити тіло, провести лінії підвісу – центр ваги завжди буде знаходитись на перетині двох або трьох ліній підвісу. Лінії підвісу розташовані завжди вертикально вниз

– до центра Землі, у напрямі сили тяжіння G. 

 

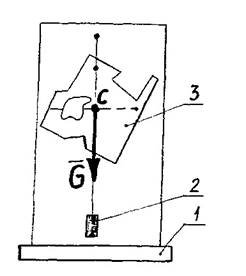
На рисунку 2 показано: 1 – установка для підвішування пластин; 2 – гирька для натягування нитки; 3 – складна однорідна пластина.

Точка С – точка перетину ліній підвісу; G - сила тяжіння пластини.

 

 

Рисунок 2.

 Аналітичний спосіб полягає у визначенні координат С за формулами. Для об’ємного тіла треба визначити три координати: X_C, Y_C і Z_C; для пластин – дві: X_C і Y_C. Цей спосіб розглянемо далі на прикладі задачі до розрахунковографічної задачі.

При визначення центра ваги треба знати такі його властивості:

-  якщо предмет має вісь симетрії або дві осі симетрії, то центр ваги завжди знаходиться на цій осі або у точці перетину осей симетрії, наприклад: круг, квадрат, прямокутник, двотавр, швелер тощо;

-  центр ваги може знаходитись поза матеріальною частиною тіла; в цьому випадку точку опори треба створити штучно – на перетині двох натягнених ниток, які співпадають з лініями підвісу;

-  центр ваги тіла завжди розташовується найближче до центра Землі;

-  центр ваги тіла займає постійне положення в межах тіла або пластини при будь-якому їх розташуванні у просторі.

Знання цих властивостей дає змогу перевірити правильність визначення центра ваги і зменшити обсяг обчислень у два рази при застосуванні аналітичного способу.

 Приведемо кілька прикладів визначення центра ваги для круга, півкруга, прямокутника і різних трикутників (рисунок 3).

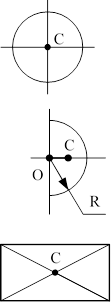
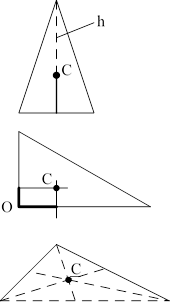Точка С – на відстані

Точка С – на

1/3 висоти h від

перетині осей основи трикутника

Точка С – на відстані

Точка С – на осі

1/3 ^{довжини кожного} симетрії, ОС=0,424R

катета від вершини О

                                                               Точка С – на перетині                                   Точка С – на

діагоналей перетині медіан прямокутника

 

Рисунок 3.

У техніці і будівництві часто використовують спеціальні металеві стандартні прокатні профілі – двотаври, швелери, кутники. Всі геометричні характеристики для них знаходяться в спеціальних таблицях, в тому числі координати центра ваги – точки С. В таблицях вони позначаються Z_O, X_O, Y_O; їх величина залежить від номера профіля.

Кілька прикладів приведено на рисунку 4.

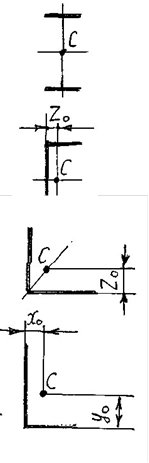Двотавр – точка С знаходиться на перетині осей симетрії;

 

 

Швелер - точка С знаходиться на осі симетрії на відстані Z_O від стінки;

Кутник рівнополочний – точка С на бісектрисі на відстані

Z_O;

 

Кутник нерівнополочний – точка С будується за координатами X_O та Y_O.

 

Рисунок 4.

Приклад позначення координат центра ваги – точки С – X_С та Y_С складної пластини показано на рисунку 5:

 

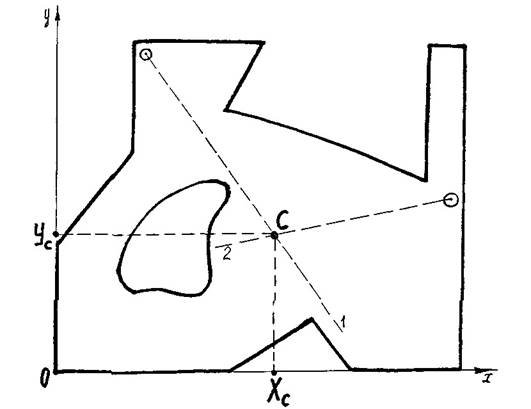
Рисунок 5.

Для визначення координат точки С складної пластини або складного перерізу застосовуються дві форми (без доведення):

                                   _X C _  Ai  X i _ A₁  X ₁  A₂  X ₂  A₃  X ₃ ;

                                                                        Ai                                            A1  A2  A3

                                                                 ∑Ai _Yi                A₁ Y₁  A₂ Y₂  A₃ Y₃

                               _YC _{                  }                                        ,

                                                                    ∑Ai                                      A1  A2  A3

       де      А₁, А₂, А₃ – площі окремих частин складного перерізу, яким присвоєні постійні номери в задачі. Значення площ обчислюються за формулами або знаходяться за відповідними таблицями в мм² або см²;                  X₁, Y₁; X₂, Y₂; X₃, Y₃ – координати точок С₁, С₂, С₃ – зарані показаних на рисунку і знайдених відповідно правилам, в мм або см;               Площі А₂ і А₃ можуть бути від’ємними, якщо частина площі пластини відсутня.

            На рисунку 6 показані позначення у відповідності із формулами:

 

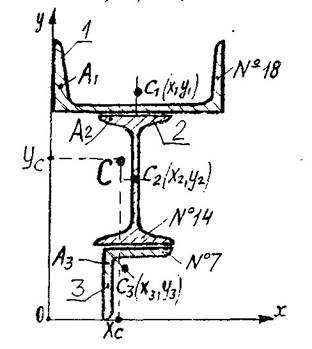
Рисунок 6.

       За визначеними координатами Х_С і Y_C на кресленні будується загальний центр ваги складного перерізу – точка С (рисунок 6).

           

3 ОСНОВНІ ВІДОМОСТІ ПРО ТЕРТЯ

 

       ТЕРТЯ – це явище, яке дуже поширене в природі і в техніці. Тертя завжди існує між поверхнями двох тіл, що дотикаються.

 СИЛА ТЕРТЯ – це сила, яка виникає при русі одного тіла по поверхні другого, має напрям протилежний руху. Сила тертя відноситься до реактивних сил.

 Класифікацію тертя за наявністю і характером руху показано у вигляді таблиці 1.

            Таблиця 1.

 

 

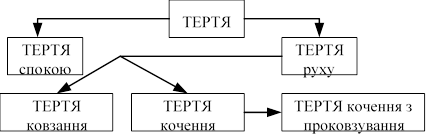
       явище тертя вивчали вчені Леонардо да Вінчі, Г. Амонтон, Ш. Кулон.  Сили тертя – це сили опору руху тіла. Причини тертя – шорсткість поверхонь тіл, міжмолекулярне зчеплення матеріалів тіл – особливо це проявляється, коли поверхні дуже гладенькі, тіла сильно притиснуті без щілин, між поверхнями тіл відсутнє змащення.

            Тертя має дві якості – воно може бути і корисним, і шкідливим.

Позитивні якості тертя використовуються в техніці:

-       в пасових передачах;

-       у фрикційних передачах і варіаторах;

-       в гальмових пристроях;

-       в роботі прокатних станів;

-       в конвеєрах і транспортерах;

-       в роботі фрикційних муфт; -в роботі лебідок, автомобілів;

-       в побутових приладах.

        

Але в багатьох випадках втрати на подолання сил тертя досить великі.

Вчені і інженери знайшли багато засобів для зменшення сил тертя:

-       заміна тертя ковзання тертям кочення; це запропонував ще у 15ст. Леонардо да Вінчі, який першим придумав підшипники кочення;

-       застосування змащення – масла, мазі, твердих змащень; в цьому випадку тертя між твердими поверхнями замінюється тертям шарів змащення, опір стає набагато меншим (рисунок 2);

-       використання шліфованих або полірованих поверхонь. Але якщо між такими гладенькими поверхнями буде відсутнє змащення, може виникнути адгезія – тобто злипання матеріалів при швидкому русі деталей за рахунок видаленого тепла і великих сил притискування;

-       підбір матеріалів деталей, що дотикаються і рухаються, можна підібрати антифрикційні пари матеріалів: сталь і чавун, сталь і бронза, сталь і латунь, що і застосовується у гвинтових передачах, черв’ячних передачах, у водопровідних кранах. Є спеціальний сплав – БАББІТ (із свинцю, олова, міді і сурми); цей сплав використовується для втулок підшипників ковзання – антифрикційний сплав (рисунок 3).

 Застосування змащень зменшує сили тертя в середньому в 10 разів!

 Заміна підшипників ковзання в машинах на шарикові або роликові підшипники кочення зменшує сили тертя в 30 разів (рисунок 4).

 Але інколи тертя треба збільшити:

-       під час ожеледиці тротуари посипають піском;

-       застосовують шорсткі матеріали;

-       шини автомобілів виготовляють не гладенькими, а під час ожеледиці на колесах машин закріплюють спеціальні ланцюги для збільшення зчеплення з дорогою.

ТЕРТЯ КОВЗАННЯ

 У 18 ст. Французькі вчені Амонтон і Кулон сформулювали три ОСНОВНИХ ЗАКОНИ ТЕРТЯ:

1.     Сила тертя F_T прямо пропорційна нормальній реакції N, тобто F_T~N;

2.     Сила тертя не залежить від величини площ тертьових поверхонь;

3.     Сила тертя залежить від матеріалів тіл, фізичного стану тертьових поверхонь, наявності і виду мастила (вода, масло, мазь), його густини і хімічного складу.

Розглянемо зв’язок між силами G, N, F_руш, F_T, R на рисунку 1:

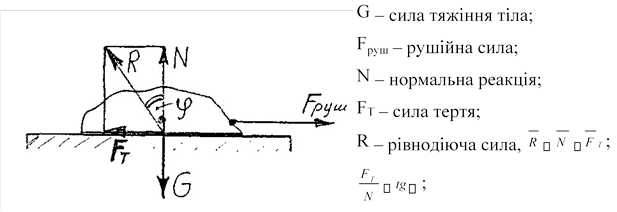
                                    Рисунок 1.                              φ – кут тертя.

 Тіло буде зберігати стан спокою доти, доки сила рушійна F_руш не стане більшою від сили опору руху тіла – сили тертя F_T.

            Умова руху F_руш > F_T.

 За законом Кулона F_T=f·N, де f – це коефіцієнт тертя ковзання, величина безрозмірна. Сила тертя не може бути більшою добутку f·N. Тому момент початку руху тіла F_T=N·tgφ, звідки f= tgφ.

            Залежно від кількості мастила між поверхнями види тертя поділяють на:

-                   сухе тертя, коли мастило зовсім відсутнє;

-                   граничне, коли є тонка плівка мастила;

-                   рідинне, коли тертьові поверхні розділяє товстий шар мастила.

 

Рисунок 2 – Сухе тертя (а); рідинне тертя (б).

          

 

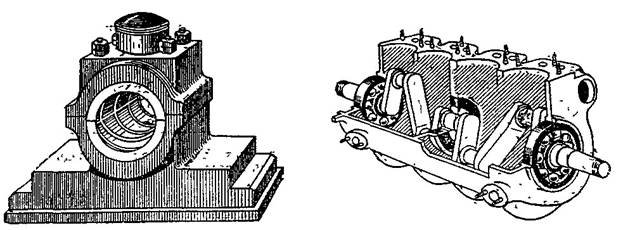
Рисунок 3 – Підшипник ковзання.                    Рисунок 4 – Колінчатий вал двигуна на шарикових підшипниках.    Коефіцієнти тертя в різних умовах визначають на дослідах, їх значення знаходяться в довідниках. Це треба знати при рішенні задач механіки з урахуванням сил тертя F_T.

       Встановлено, що для стану спокою коефіцієнт тертя f має найбільше значення. Приведемо кілька прикладів в таблиці 2.

            Таблиця 2.

1. Метал по металу насухо	f=0,15…0,30
2. Метал по металу з мастилом	f=0,10…0,18
3. Дерево по дереву насухо	f=0,40…0,60
4. Сталь по льоду	f=0,02

 

 Коефіцієнт тертя ковзання під час руху звичайно менший, ніж для стану спокою.

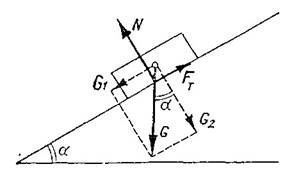
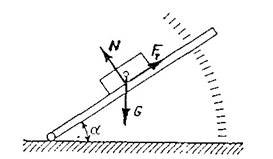
Рівновага тіла на похилій площині

Розглянемо тіло, яке лежить на шорсткій похилій площині, що утворює кут α з горизонтальною площиною (рисунок 5). Розкладемо силу G на складові G₁ і G₂, паралельну і перпендикулярну до похилої площини. Модулі цих складових визначимо за формулами:

                                                    G₁=G · sin α,                  G2=G · cos α.

Складова G₂ зрівноважується реакцією N похилої площини.

Тому G₂ = N = G · cos α.

Складова G₁ намагається зрушити тіло вздовж похилої площини. Ця складова частково або повністю зрівноважується силою тертя; за другим законом тертя ковзання її максимальне значення

F_T = f · N = f  · G · cos α, 

де f — коефіцієнт тертя ковзання тіла по похилій площині. Щоб тіло на похилій площині було в рівновазі,  рушійна сила G₁ має дорівнювати за модулем силі тертя F_T, тобто

G sin α = f  · G · cosα або tg α = f = tg φ,

                    Рисунок 5.                              звідки

α = φ.

Якщо кут  між  похилою   площиною і горизонтом дорівнює куту тертя,  то тіло, яке лежить  на  похилій  площині,   під дією власної сили тяжіння або рівномірно сковзатиме вниз, або буде в стані спокою. Щоб тіло, яке лежить на похилій площині, не сковзало вниз під дією власної сили тяжіння, має здійснюватись умова

α < φ.

    

Похилою площиною із змінним кутом нахилу до горизонту користуються для експериментального визначення кута тертя φ і коефіцієнта тертя f (рисунок

6).

 

коли α = φ, f = tg α.

Рисунок 6.

            Результати експерименту покажемо в таблиці 3.

            Таблиця 3.

Матеріал площини                                                      ^Сталь

Матеріал зразків                        Сталь             Чавун        Алюміній       Латунь          Деревина

                                 

Кут тертя φ, град.

Коефіцієнт тертя ковзання                                               f = tg α= tg φ

 

Приклад рішення задачі з урахуванням сил тертя.

Умова задачі: до вала прикладена пара сил F F з моментом М=100 Нм. На валу закріплений гальмівний шків діаметром D=500 мм.

 Знайти силу Q, з якою необхідно притиснути до колеса гальмівні колодки, щоб вал залишився нерухомим, якщо коефіцієнт тертя між матеріалом шківа і колодки f=0,25 (рисунок 7).

 

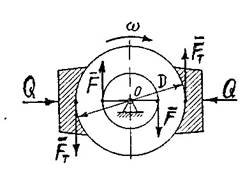
Рисунок 7.

Рішення

                              Момент М=100 Нм обертає вал за годинниковою стрілкою. Між

колодками і гальмівним шківом виникають сили тертя F _T F _T , які утворюють гальмівний момент , напрям якої проти годинникової стрілки. Таким чином вал знаходиться під дією двох пар сил.

 Для рівноваги пар F F та F _T F _T , які діють в одній площині, необхідно і достатньо, щоб алгебраїчна сума моментів пар дорівнювала нулю.

            Складемо рівняння рівноваги:

                    M _i  ⁰,           M  F_T  D  ⁰ ;

звідкіля              F_T  ^M _ ¹⁰⁰ _ 200 H . D              0,5

            За основним законом тертя

                       F_T  f  ^Q ,

звідкіля              Q _ ^FT _ ²⁰⁰ _ 800 H . f 0,25

Відповідь: Q=800 H.

ТЕРТЯ КОЧЕННЯ

 Тертя кочення значно відрізняється від тертя ковзання тим, що площа дотику тертьових поверхонь значна менша, сили опору руху менші.

 Розглянемо циліндр (колесо), який рівномірно перекочується по поверхні, яка трохи деформується (рисунок 8). Рушійна сила F горизонтальна. Сили N і F_T – реактивні сили в точці А; N – реакція, нормальна до недеформованої опорної площини; F_T – сила тертя кочення.

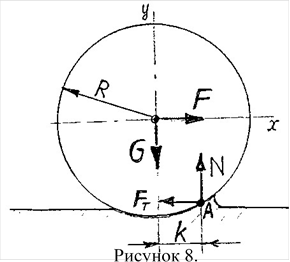Складемо три рівняння рівноваги котка:

  F_ix  0; F  F_T  0 ;

 F_iy  0; N G  0

 M _A  0; F  R  G  k  0

З цих рівнянь маємо:

                                                                                                 F = F_T ;

 N =G ;

F  R  G  k ,

Звідкіля рушійна сила F дорівнює:  F _ ^{G  k} , R Добуток F  R  M - момент кочення; добуток G  k  M _T - момент тертя.

 Коефіцієнт тертя кочення k визначають дослідами при різних умовах, його значення знаходяться у довідниках. Кілька прикладів значень коефіцієнта k,см приведено в таблиці 4.

            Таблиця 4.

                                       Матеріали тіл котків                             Значення k,см

1.            М’яка сталь по м’якій сталі          0,005

2.            Загартована сталь по загартованій сталі          0,001

3.            Чавун по чавуну        0,005

4.            Дерево по сталі          0,03...0,04

5.            Дерево по дереву       0,05...0,08

6.            Гумова шина по шосе          0,24

 

 З таблиці добре видно, що на тертя кочення дуже впливає твердість поверхонь тіл.

СТОРІНКА ДЛЯ ДОПИТЛИВИХ

1.                       Тертя – явище, яке існує об’єктивно, його не можливо позбутись його можна тільки зменшити.

2.                       При терті механічна енергія переходить в тепло – це відкриття було зроблено у 18 ст.

3.                       Ідею молекулярного зчеплення між гладенькими тертьовими поверхнями у 18 ст. відкрив І. Дезагюлье, назвав це явище адгезією. Адгезій ні зв’язки дуже важко зруйнувати.

4.                       Велике скло, яке довго лежало на другому склі, важко зсунути: виникає чистий контакт між молекулами; коефіцієнт тертя між однорідними матеріалами більший, ніж між неоднорідними.

5.                       Для двох тертьових поверхонь не можна призначити однаковий тип обробки поверхонь: структура повинна бути різною, буде менший опір переміщенню деталей.

6.                       Кут нахилу кузова самоскида не однаковий – він залежить від речовини в кузові: сухий чи вологий пісок, асфальт, вугілля...

7.                       Умова самогальмування α ≤ φ використовуються у гвинтових парах, різьбах, черв’ячних гвинтах. Проблема само відгвинчування існує на транспорті, її вивчають в інституті в Англії.

8.                       Для меншого стирання шасі літаків їх попередньо розкручують перед дотиком до бетону.

9.                       При швартуванні кораблів канат закріплюють навколо кнехта разів три, використовуючи сили тертя між канатом і тумбою.

10.                  Щоб витратити менше зусиль на переміщення санок, треба прив’язати довгу мотузку.

 

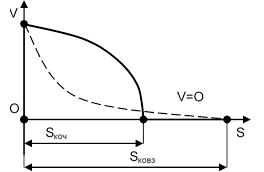
11.                  Під час небезпеки наїзду гальмувати треба юзом – ковзанням: швидкість зменшується швидше, хоча гальмівний шлях більший. При цьому кінетична енергія удару mV ²

      E =     буде значно меншою, пропорційно

2

V². гальмування коченням зберігає шини.

                                                                                      Рисунок до прикладу 11

12. Між лезами ковзанок або бобслеєм і ковзанкою виникає змащувальна плівка – тертя перетворюється в тепло, розігріває лід.

4 КІНЕМАТИКА

4.1 ОСНОВНІ ПОНЯТТЯ КІНЕМАТИКИ

Кінематика точки

 Кінематика - це розділ теоретична механіки, в якому вивчають механічний рух твердих тіл без урахування їх мас і діючих на них сил.

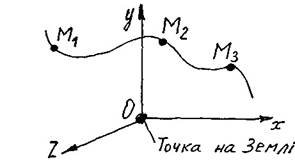1. Механічний рух - це зміна положення одного твердого тіла відносно інших тіл у просторі і в часі. Звичайно рух тіл (переміщення) розглядають відносно нерухомої системи координат xyz, яка нерухома відносно Землі (рисунок 1)

Взагалі рух, простір і час – основна форма існування матерії. Це об’єктивна реальність, яка існує поза свідомістю людей.

Рисунок 1

 Механічний рух - це найпростіший з усіх видів руху, тому що спостерігається неозброєним оком.

 Приклади механічного руху твердих тіл: рухаються планети Сонячної системи навколо Сонця, рухаються космічні кораблі, штучні супутники Землі, військові балістичні ракети, кулі, спортивний спис, або спортивне ядро чи молот, футбольний чи волейбольний м’яч, літаки, машини, гелікоптери, баржі, судна, човни.  Започаткував вивчення науки "Кінематика" вчений

Аристотель в IV столітті до нашої ери.

2. Способи завдання руху точки.

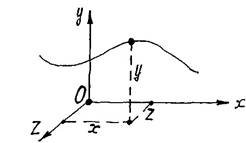       Положення матеріальної точки (або твердого тіла) в просторі визначаються трьома координатами (абсциса x, ордината y, апліката z) по відношенню до прямокутної (декартової) системи координат Oxyz (рисунок 2) Ці координати є функціями часу t:

x  f₁(t) 

 y  f₂ (t) Три рівняння, які визначають закон

^z  f₃ (t) поступального руху точки в координатній формі.

Рисунок 2

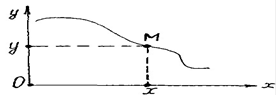 Якщо точка рухається в площині, закон руху точки визначається двома рівняннями (рисунок 3): x  f₁(t)

                                                                                                                                         

_ y  f₂ (t)

 

Рисунок 3 Приклад.

Рух точки заданий двома рівняннями ^_^{x  2t} .

_ y  3t Підставляємо різні моменти часу:

t0 = 0;          t1 =1c;	t2 =2c   і  т.ін.
При t0 = 0	При t1 = 1c			При t2 = 2c
x0 = 0;	x1 =2м;			x2 = 4м;
y0  = 0;	y1 =3м;			y2 = 6м.

Якщо виключити час t із обох рівнянь - отримаємо рівняння траєкторії:

                                         t = x ;          t = y .

                                                                             2                             3

Або: 3x  2 y  0 , тобто точка рухається по прямолінійній траєкторії (рисунок 4).

 

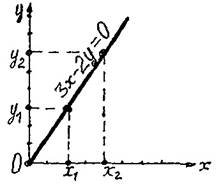
Рисунок 4

 Звичайний спосіб полягає у тому, що рух точки задають її траєкторією і законом руху (рівнянням руху) по цій траєкторії:  S = f (t)

Тут S - відстань точки від початку відліку (точки О), що є функцією часу; t - час руху точки від початкового моменту. Щоб знайти положення точки на траєкторії, треба в рівняння руху підставити час.

Приклад.

Точка рухається по прямій траєкторії згідно рівнянню : S = 0,5t ² .

Який шлях пройде ця точка за 3с від початку відліку (рисунок 5)

При  t₀ = 0                При t₁ = 1c                    При t₂ = 2c           При t₃ = 3c

            S₀ = 0;                  S₁ = 0,5м;                       S₂ = 2м;               S₃ = 4,5м.

 

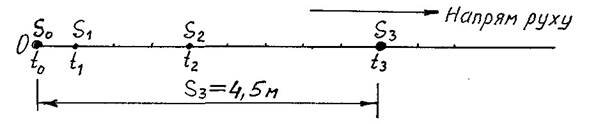
Рисунок 5

 Примітка: шлях S, пройдений точкою, збігається з відстанню S від початку відліку тільки тоді, коли точка весь час рухається в одному напрямі і початок її руху збігається з початком відліку.

 

3.                       Траєкторія - це геометричне місце положень рухомої точки, або це лінія, по якій переміщується рухоме тіло.

 Залежно від форми траєкторії бувають: прямолінійні та криволінійні, замкнені та розімкнені, плоскі та просторові.

Різні тіла, предмети, деталі рухаються по різним траєкторіям (рисунок 6).

 

Рисунок 6

 По складним траєкторіям рухаються машини, автобуси, трамваї, літаки, футболісти, пішоходи, підводні човни і т. ін.

4.                       Час - це незалежна величина, яка неперервно змінюється в одному напрямі. В кінематиці розрізняють такі поняття, пов’язані з часом:

       t₀ - початковий момент часу;  t₁ і t₂  - дані моменти часу;

 t₂ - t₁ =∆t - проміжок часу (час, що проходить між двома фізичними явищами) (рисунок 7)

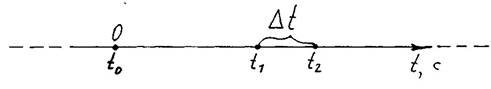
Рисунок 7

За одиницю часу приймається секунда (с).

5.                       Відстань та шлях.

 Відстань - це довжина ділянки траєкторії, відрахованої від початку відліку. Відлік відстані можна вести в обидва боки від початку відліку, тобто відстань S величина алгебраїчна, може бути додатною (S>0) або від’ємною (S<0) (рисунок 8).

Шлях L - величина завжди додатна, при русі тіла завжди зростає. Відстань S та шлях L вимірюються в метрах (м).

 

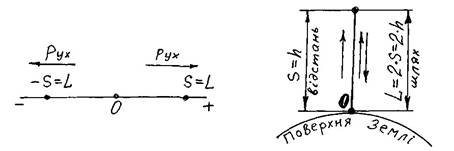
Рисунок 8

При поступальному русі тіла відстань S (м) змінюється з часом: S = f(t).

6.                       Швидкість - векторна величина, характеризує швидкість переміщення тіла (точки) по траєкторії.

Залежно від швидкості рухи бувають: рівномірний та нерівномірний.

Нерівномірний рух характеризується середньою швидкістю V _cep (рисунок 9).

S

                                                                                                                                    V cep   .

t

                                                                                                                                   При ∆t → 0          ∆S → 0,

тому миттєва швидкість  визначається так: V _ lim ^S _ ^dS _ S  _ f (t) .

                                                                                                                                           t0 t          dt

Рисунок 9

S V =     = const t

                      Якщо швидкість постійна, рух називають рівномірним: .

Одиниця швидкості: [V ] == довжина = метр = м .

                                                                                              час              секунда          с

Вектор V _cep спрямований по хорді дуги довжиною ∆S; вектор миттєвої швидкості V спрямований по дотичній до траєкторії в даній точці (рисунок 9).

Приклад.

За який час світло подолає відстань від Сонця до Землі?

Відстань S = 150х106 км;	швидкість світла Vcв = 3х105 км/с
Рух світла рівномірний, 6	V = const, тому V S , звідкіля t = S . t     V
150 10

Обчислення: t      5     500 c  8хв.20с .

3 10

7. Прискорення - це векторна величина, яка характеризує бистроту зміни швидкості за одиницю часу. Розрізняють середнє прискорення а_сер і миттєве а (рисунок 10):

                                                                                  a _cep  (V  V )  V  V ; при ∆t → 0  а_сер→ а:

                                                                                                      (t  t)  t            t

                                                                                                                            V        dV

Рисунок 10                                 a  lim a _cep  lim                     V   S   f (t) .

                                                                                              t0                           t0 t            dt

                           При прискореному русі вектори миттєвої швидкості V і миттєвого

прискорення a співпадають, а при сповільненому русі вектори V та a - протилежні (рисунок 11)

 

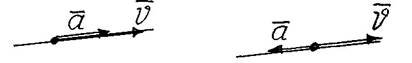
Рисунок 11

Приклад

Нерівномірний прямолінійний рух заданий рівнянням: S = 0,5t² + 2t + 40 Визначити швидкість і прискорення в кінці 10-ї секунди та шлях S, пройдений за 10 сек.

Рішення:

При t=0         S_O=40м;

При t=10 S₁₀=0,5·10²+2·10+40=110м; За        10с    S= S₁₀ – S_O =110 – 40=70м;

Швидкість V  S   0,5  2 t  2  12 ^м ;

с м

Прискорення a  V   S  (1t)  ¹   ,

с

 

тобто рух точки рівноприскорений.

Прискорення земного тяжіння g величина постійна: g=9,81 м/с².

8. При криволінійному русі повне прискорення a складається із двох частин: _a - дотичного, _a - нормального (рисунок 12). Тобто a = a + a_n , або a = a +a .

Тут a _τ - дотичне прискорення, характеризує зміну швидкості тільки за величиною. 

Обчислюється за формулою: a_τ= ^dV = V ′= S ′′. dt

Рисунок 12

Якщо вийде + a_τ - рух прискорений, якщо вийде –a_τ - рух сповільнений.

Тут a _n - нормальне (доцентрове) прискорення, характеризує зміну вектора

V 2 швидкості за напрямом. Обчислюється за формулою: a_n =  , де ρ - радіус ρ

кривизни траєкторії в даній точці. Вектор a _n завжди спрямований по нормальній осі "n" до центру кривизни траєкторії.(рисунок 13).

 

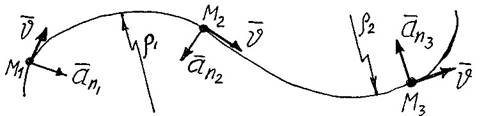
Рисунок 13

Запитання для закріплення теми:

Чи може точка, яка рухається рівномірно, мати прискорення?

Відповідь:  Може, якщо точка рухається по криволінійній траєкторії: V=const, a_τ=0, _an = ^V2 ρ

;

виходить, що а=а_n.

Тобто в цьому випадку завжди є нормальна (або доцентрова) складова повного прискорення.

        

Якщо точка рухається по траєкторії в формі кола, то доцентрове прискорення обчислюється за формулою: 

V 2  a_n = , де R – радіус кола (тобто ρ = R = const  для кола). R

 Якщо друга похідна S˝ дорівнює нулю, тобто a_τ  S   0 , це означає, що точка рухається рівномірно, без прискорення V=const.

 Якщо похідна S˝ дорівнює будь-якому числу, це означає, що рух точки рівнозмінний: рівносповільнений – якщо число від’ємне, рівноприскорений – якщо число додатнє.

Приклад для закріплення теми: 

Поступальний рух точки заданий рівнянням: S = t²+3t+1.

Визначити швидкість V і прискорення a в момент часу t = 5с. Рішення:         V  S   (t ²  3t  1)  2t  3 ;

                     a  V   S   (2t  3)  2 .

Обчислення при t = 5с: V  2 t  3  2 5  3  13 ^м ;

с

                                                                           a = 2 м₂ = const . с

Висновок: 

Рух точки є рівноприскореним.

 

 

 Прикладом рівносповільненого руху може бути рух тіла, що підкинули вертикально вгору. Прикладом рівноприскореного руху є вільне падіння тіла в полі тяжіння Землі. Величину прискорення земного тяжіння ^{g = 9,81 м/с2} визначив ще в 17 сторіччі Галілео Галілей.

4.2 ОБЕРТАЛЬНИЙ РУХ ТВЕРДОГО ТІЛА НАВКОЛО НЕРУХОМОЇ ВІСІ

       Обертальний рух твердих тіл – явище дуже поширене. В усіх машинах, приладах обертаються деталі і вали, зубчасті колеса, шестірні, шківи, зірочки, диски, заготовки, ротори, блоки.

       При обертальному русі тіла будь-яка точка тіла рухається по траєкторії у формі кола, центр якого знаходиться на нерухомій осі і в площині, перпендикулярній до цієї осі.

 Основні параметри обертального руху позначаються так: φ, ω, ε, n (рисунок 1)  

1.                        φ – кутове переміщення:   f t;     вимірюється в рад, обертах:  1об = 360⁰ = 2π рад.

 

2.                        ω – кутова швидкість; 

 при рівномірному обертанні         ;

t

вимірюється в рад с ; 1 с ; с ^1

3.                        ε – кутове прискорення; при рівнозмінному обертанні   t ; вимірюється в рад с² ; 1 с² ; с ^2 .

 

4.                        n – частота обертання  - швидкість  обертального руху в обхв або 1хв Рисунок 1.

 

                      Встановимо залежність між двома швидкостями – кутовою ω ( рад с ) та

частотою     обертання     n     (обхв ):          вони  n; 1хв  60с;	пропорційні	між	собою:
 рад                  2                                                   тоді:                n                                                                                  с                    60с	 рад    ,  с 

або: 

   n  0,1 n для наближених обчислень ;

 

30  _або: n    9,55   10 ^. 

Приклад:  вал двигуна обертається зі швидкістю 750^обхв . Визначити кутову швидкість валу двигуна.

_Тобто: n  750 обхв ;       ω –?

                                            n                                 3,14  7501

Рішення:                                   78,5 радс          (або      n  75 радс)

                                              30                                              3010

Встановимо залежність між швидкостями ω, V, n:

  f (t)

                                         ^_V _ f (t)

^S  f (t)

Із рисунка 1 видно, що S   R. При рівномірному русі V  S t, або  V   Rt;  але   t  при рівномірному русі.

 

                                                     Тоді:    V   ^R ,        Де R – радіус колеса.

       Із цієї формули видно, що швидкість точки тіла пропорційна відстані від цієї точки до центра обертання.  Для точки А  ОА = R, тобто 

U_A   R  ^OA

Для точок В і С швидкість VВ та VС менша VА: дивимось на рисунку (рис. 2):

V_A   OA

V_B   OB ;

V_C   OC

V_O   O : V_A  OA або

                                                                                                                                          V_B          OB

 

Рисунок 2. Перетворимо формулу 2, замінивши в ній:
d                       n                                                      R      і                                                                      2                       30	Або:

V	  d  n  60

                                                                    n          d dn

                                                     V                  

                                                                      30        2          60

 

        

Приклад: заготовка деталі (колеса, диска, шківа) має діаметр ^{d  200мм} ; при обточці її поверхні швидкість різанняV  1,2 мс . З якою швидкістю повинна обертатись заготовка?

 

_Дано: V  1,2 мс

        d  200 мм  0,2м             n - ?

 

Рішення: 

d  n

основна формула (3): V                      

60

60 V розрахункова формула: n 

  d

об

Обчислення: n  114                         хв

Відповідь: частота обертання заготовки повинна бути n  114 обхв .

4.3 СПОСОБИ ПЕРЕДАЧІ ОБЕРТАЛЬНОГО РУХУ

У техніці обертальний рух і енергія від джерела енергії (електродвигуна) до користувача (робочої машини) передається за допомогою різноманітних механізмів, які називають ПЕРЕДАЧАМИ.

Зобразимо блок-схему:

 

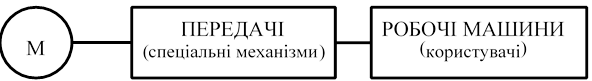
ЕЛЕКТРОДВИГУН	Зубчасті		Верстати
(джерело енергії)	Пасові		Преси
Основні характеристики:	Ланцюгові		Конвеєри
Р(кВт) — потужність	Черв’ячні		Транспортери
двигуна;	Фрикційні		Ескалатори
n (об/хв) - частота	Гвинтові		Лебідки
обертання вала	Рейка-колесо		Крани
двигуна.	Кулачкові

Функції, які виконують передачі, дуже різноманітні.

1.             Деякі передачі здатні передавати енергію на велику відстань (до 15 метрів – пасові, до 8 метрів - ланцюгові).

2.             Більшість передач здатна значно зменшувати (або й збільшувати) кутову швидкість ротора двигуна до необхідної для робочої машини в декілька разів. (Двигуни більш економічні ті, у яких велика частота обертання ротора, а робочим машинам потрібна набагато менша).

3.             Водночас із зменшенням швидкості обертання ротора двигуна передачі здатні збільшувати обертаючий момент - силову характеристику двигуна - в декілька разів.

4.             Деякі передачі здатні перетворювати обертальний рух ротора двигуна у зворотно - поступальний, переривчастий або коливальний рух робочої машини.

Тому передачі дуже поширені в усіх галузях техніки. Згадайте, де ви їх бачили.

Деталі кожної передачі мають окрему назву, наприклад:

-                    зубчаста передача — шестірня і зубчасте колесо;

-                    пасова — шківи і пас;

-                    ланцюгова — зірочки і ланцюг;

-                    черв’ячна — черв’ячний гвинт (черв’як) і черв’ячне колесо; - фрикційна — котки або ролики.

Ці колеса закріплені на валах, які мають назву — ведучий вал або ведений. Кінці валів закріплені в підшипниках ковзання або кочення, завдяки яким вали легко обертаються разом із закріпленими на них колесами. Колесо і вал, які першими отримують енергію від двигуна, називаються ВЕДУЧИМИ - вони мають номер 1.

Колесо і вал, які обертаються завдяки зачепленню з ведучими (або завдяки тертю між ними), називаються ВЕДЕНИМИ- вони мають номер 2.

Якщо ведуче колесо менше веденого, передача працює як знижувальна. Такі передачі називають РЕДУКТОРИ. Далі будемо вивчати саме такі передачі.

Основною характеристикою будь-якого редуктора є передаточне число U, яке показує, у скільки разів знижується швидкість від ведучого валу до веденого за рахунок цієї передачі.

Виведемо формулу для обчислення передаточного числа U , загальну для усіх передач — редукторів. За приклад беремо найпростішу фрикційну передачу, яка працює без проковзування, тобто лінійні швидкості точок дотику котків однакові:

V₁=V₂

Використаємо відомі нам із попередніх уроків залежності:

а) між кутовою швидкістю ω і частотою обертання n:

  n

                           _   - тобто ω ~ n;

30

б) між діаметром колеса d і числом зубів Z на ньому :

на більшому колесі можна нарізати більше зубів, тобто d ~ Z;

в) між лінійною і кутовою швидкостями :

d

                          V   R             або  V    .

2

     

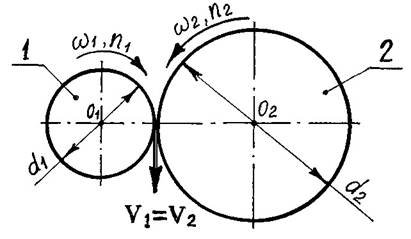
         Перетворимо останній вираз у відношення:

 

V₁  V₂

1 d₁  2 d ₂ ,

        2                2

або ₁d₁  ₂d ₂ .

 

 

 

1   u 2

1  d 2 ,          де                    -

2                    d1

основна формула для визначення передаточного числа. Для редукторів u > 1 завжди, тому що менше ведуче колесо 1 обертається швидше, ніж більше ведене 2, тобто ω₁>ω₂ завжди.

 Враховуючи, що ω₁~n₁., ω₂~n₂ , маємо ще одну формулу:      u _ ⁿ¹

n2

— ця формула показує, скільки обертів зробить ведуче колесо передачі, поки ведене колесо обернеться один раз.

                                                                                            ¹                                                   d²

                   Із доведення отримали: u             і           u   ,

                                                                                            2                                                   d1

Враховуючи, що d₁ ~ Z₁ ; d₂ ~ Z₂ — маємо ще дві формули для визначення числа u:

                                                                                            d2            Z 2

u   , d1 Z1

які можна застосовувати для визначення передаточного числа так : треба виміряти діаметри колес фрикційної чи пасової передачі d₁ і d₂, або ж порахувати числа зубів на зубчастих колесах чи зірочках ланцюгової передачі Z₁ і Z₂. Завжди d₂ > d₁, Z₂ > Z₁, тож і виходить, що u > 1 для передач – редукторів.

Виключенням є черв’ячна передача, для якої Z₁ — це є число заходів різьби на черв’ячному гвинті: воно може мати тільки такі значення : 1,2, 4. Тому черв’ячний редуктор завжди має дуже велике передаточне число, бо Z₂>>Z₁.

Завдяки цьому виходить :

Z ²

u     >>1 (може бути від 10 до 200 для одноступінчастої передачі).

Z1

                                                                                                   Z ²           100

Наприклад: Z₁ = 2; Z₂= 100, тоді u                     50

                                                                                                    Z₁                2

Напишемо загальну формулу для визначення передаточного числа u:

 u   1 2

n1                    d2              Z 2                n2                    d1                Z1

її треба запам’ятати і вміти нею користуватись.

 

Треба знати, як зображуються різні механічні передачі на кінематичних схемах. Розглянемо схеми на плакатах. Зіставимо схеми на плакатах, подані у двох проекціях, з моделями відповідних передач.

5 ДИНАМІКА. 

5.1 АКСИОМИ ДИНАМІКИ

Динаміка ґрунтується на ряді положень, що є аксіомами і називаються законами динаміки. Таких аксіом чотири:

I      аксіома – це аксіома інерції або перший закон Ньютона:

«Якщо на тіло діє урівноважена система сил, то тіло перебуває у стані спокою,         або    рухається прямолінійно      рівномірно,          або    рівномірно обертається».

                         n          

Тобто:  F _i  0 ; υ = 0 або υ = const

i1                                  ω = 0 або ω  = const.

 

II  аксіома – це основний закон динаміки або другий закон Ньютона: «Прискорення, якого надає тілу або матеріальній точці сила, має напрям сили і пропорційне модулю сили»:

                                                                   F1             d1                        F1            F2

 або  F2 d 2 d1 d 2

F  m  a

Математична формула II закону:  F = m ּ a   або  .

m - це маса тіла або точки.

Маса – одна з основних характеристик будь-якого матеріального об’єкта

(тіла):

-                   міра інертності тіла при поступальному русі;

-                   кількість матерії у даному тілі;

-                   гравітаційна постійна величина для кожного тіла.

F

  m  const a

Сила тяжіння тіла G визначається за формулою: G = m ּ g, де g – прискорення вільного падіння тіла. В умовах Землі g має такі значення: на полюсах Землі g  9,83 м / с ² , для Москви g  9,81м / с ² , на екваторі g  9,78 м / с ²

(дивись схему сил на плакаті).

         

Розглянемо малюнки, із яких зрозуміла залежність між F, m, a або G, m, g:

        F                         а                                             ^m₁                               ^m     m

                                                  

                                                                      

                                                                     

   3  F                        ₃  _m      a                                                       

                                                                                         

                                                                                                                                                                     2 g = const

                                                                                                                   G₁  m₁  g;                         G₂  m₂  g

Одиниці сили:

[F] = [m]∙[a] = маса прискорення = ньютон

м Н  кг  2 с

Тобто  = ньютон

1 кН = ^{10 3} Н = 1000 Н = кілоньютон

1 МН = ^{10 6} Н = 1000000 Н = меганьютон

1 кгс = 9,81 Н ≈ 10 Н; 1 Н ≈ 0,1 кгс

 

III          аксіома – аксіома взаємодії, або III закон Ньютона: сили взаємодії двох тіл завжди однакові за модулем і протилежно напрямлені по одній прямій.

                                                                                                                       

 

Тобто однобічної дії одного тіла на друге не буває, тобто всі сили природи – парні: дія дорівнює протидії. Цю аксіому можливо розглянути у

такому вигляді: F₁  F₂ або m_1  a₁  m₂  a₂ або ^a1  ^m2 .

                                                                                                                            a2             m1

З останньої формули видно, що прискорення, які отримують два тіла при взаємодії зворотно пропорційні масам цих тіл. III закон Ньютона став основою для розробки теорії реактивного руху російським вченим Ціолковським К.Є.

         

IV          аксіома – принцип незалежності дії сил: коли на тіло діє одночасно кілька сил, то його прискорення дорівнює векторній сумі прискорень від кожної сили окремо.

                                                                                                                       

                                                  F1  m  a1

     F2  m  a 2      F3  m  a3

                                                 F4  m  a 4

                                                   F₁  F₂  F₃  F₄  R  m  a

 

 

Тобто m _ a₁ + m _ a ₂ + m _ a ₃ + m _ a ₄ = m _ a , поділимо на m: a₁ + a ₂ + a₃ + a ₄ = a ,

n a   a i1

 або .

5.2  РОБОТА ТА ПОТУЖНІСТЬ

 

Робота і потужність – це механічні величини, що характеризують дію сил та зв'язок цієї дії з шляхом, часом, видом руху та іншими параметрами динаміки. Приклад 1. Робота сталої сили на прямолінійній ділянці шляху:

 

W  F  S  cos α

 

Робота W – це міра дії сили, прикладеної   до      матеріальної точки під час її переміщення. Робота – величина скалярна.

 

 

Одиниця роботи:

[W] = [F]٠[S] = Н٠м = джоуль (Дж).

Окремі випадки обчислення роботи:

                                      1.1.   0                                                     W  F  S  W_max ;

                                       1.2. _{ } 90_                                                 W _ 0 ;

                                     1.3.   180                                                W  F  S .

 

Сили, які виконують додатну роботу, називають у техніці рушійними.

Сили, які виконують від’ємну роботу, називають силами опору (сили тертя, опору середовища – води, мастила, повітря).

Робота сили тяжіння дорівнює нулю, коли тіло рухається по горизонтальній площині, додатна – коли тіло рухається вниз (напрям сили тяжіння та напрям руху співпадають); від’ємна – коли тіло рухається вгору (напрям дії сили тяжіння та напрям руху протилежні).

Приклад 2.   Робота змінної сили.

Розглянемо випадок, коли сила, прикладена до тіла не відразу вся, а зростає поступово від нуля до значення F. Побудуємо графік, який виражає залежність між F та S:

 

Робота у цьому випадку обчислюється як площа трикутника: дорівнює половині добутку сили на шлях (переміщення).

 

порівняння з        прикладом 1 графік, коли F = const: у цьому робота обчислюється як площа прямокутника:

W = F٠S                

 

Приклад 3. Робота сталої сили, прикладеної до обертового тіла. 

Нехай до диска у точці А прикладена дотична сила F, яка обертає його навколо центра О. Така сила виникає між колесами зубчастих, фрикційних,

черв’ячних та інших передач під час їх роботи.

Знайдемо роботу сили у цьому випадку:

 

W = F٠S;

але S = R٠φ (згідно рисунку); тоді W = F٠R٠φ.

Замінимо F٠R = М_об (момент обертаючий).

Одержимо формулу: W = М_об٠φ.

 

 

W  M об 

Робота у цьому випадку дорівнює добутку обертаючого моменту на кутове переміщення: 

Приклад 4. Потужність при поступальному русі.

Потужність взагалі – це механічна величина, яка характеризує швидкість

W

виконання роботи, або це робота, виконана протягом одиниці часу: P       

t

Одиниця потужності:

Дж

                    [ P ]                  ват (Вт)

с

Виведемо формули для обчислення потужності при поступальному, а потім при обертальному рухах:

                               W       F  S

P    F  ν , тобто  Р = F٠υ t           t

                                                                                                                                                         W        М ^об  φ

                    Застосуємо аналогічні перетворення формул: P                           .

                                                                                                                                                            t              t

Але ^φ  ω (кутова швидкість).

t

                   Тому               Р = М_об٠ω

 

Останню формулу у технічних розрахунках часто використовують у зміненому вигляді – для визначення обертаючого моменту М_об на валах машин та механізмів при відомій потужності та кутовій швидкості (чи частоті обертання):

                                           P π n                                                    Р         30  P                  P

М _об =     ; ω=               , тому М _об     9 ,55          , тобто  ^ω            30           π  n    π  n    n

30

P

                                                                                          М _об  9 ,55   

n

Тут треба потужність Р завжди подавати в одиницях [Вт], тоді одержимо [М_об] = Н٠м.

Підсумок: Порівнюючи формули для обчислення роботи та потужності при поступальному та обертальному рухах, легко побачити, що вони за структурою подібні:

Це сприяє їх легкому запам’ятовуванню: 

W = F٠S     Р = F٠υ W = М_об٠φ          Р = М_об٠ω

 

Тут F та М_об – рушійні силові фактори; S та φ – переміщення; υ та ω – швидкості.

 

Формули із цієї теми, які надалі треба запам’ятати:

P M об  

P M об  9,55 n

W_max  F  S P  F  v 

5.3 КОЕФІЦІЄНТ КОРИСНОЇ ДІЇ

Механізми і машини використовують для виконання корисної роботи - обробки деталей, підняття і переміщення вантажів (верстати, крани, ескалатори, конвеєри та інші). Але в них завжди є сили шкідливого опору - це сили тертя, сили опору середовища (повітря, води, мастила), які зменшують продуктивність машини.

Залежно від співвідношення корисної і затраченої роботи або потужності машини поділяють на більш або менш продуктивні. Р_затр. - це потужність двигуна.

 Продуктивність або досконалість механізму характеризує його коефіцієнт корисної дії - ККД - η:

                             PКОР                         PЗАТР  PШК            PЗАТР      PШК         1  PШК PЗАТР      PЗАТР           PЗАТР           PЗАТР           PДВ

Таким чином η <1 - завжди (або η <100%).

Чим ближче ККД до 1 (або до 100%), тим досконаліша машина. Але ніколи ККД не може бути більше 100 % - вічний двигун або машину створити неможливо.

Значення ККД для деяких поширених механізмів:

Верстати	- η = 0,80 ... (80%)
Черв’ячні передачі	- η =0,70 ... 0,95 (70% ... 95%)
Зубчасті редуктори	- η = 0.95 ... 0,98 (95% ... 98%)
Ланцюгові передачі	- η = 0,90 ... 0,97 (90% ... 97%)
Пасові передачі	- η = 0,95 ... 0,98 (95% ... 98%)

Якщо ряд механізмів з'єднано послідовно, тобто кожний наступний механізм рухається попереднім механізмом, то загальний ККД такого багатоступінчастого пристрою визначається як добуток ККД усіх механізмів:

                       ЗАГ 1СТ 2СТ 3СТ

Загальний ККД завжди менший, ніж найменший ККД окремого

механізму у пристрої.

           

ПРИКЛАД 1.  (за схемою на плакаті): Визначити загальний ККД трьохступінчастого пристрою, якщо відомо: η пас = η 3ст= 0,96 η ред = η 2ст= 0,98 η _кон = η _3ст = 0,97

Обчислення:   _1ст _2ст _3ст  0,96  0,98  0,97  0,916    η _заг = 91,6%

На подолання сил шкідливого опору втрати дорівнюють:  

                                             100% – 91,6% =8,4% 

 

ПРИКЛАД 2.   (за схемою на плакаті):

         Визначити обертаючий момент на валу двигуна, якщо відомо:

                     Р_дв=4КВт;            η _дв =750 об/хв.

           РІШЕННЯ: застосовуємо формулу, яка пов’язує Р, η та М_об.: 

P M об  9,55 n

           ОБЧИСЛЕННЯ:  M _об = 9,55 ⁴⁰⁰⁰ = 50,93 Hм

750

P M об  

          ПЕРЕВІРКА:                     ;     ω  π    n  3,14  750  78,5 рад

                                                                                                              30                 30                           с

                                          M _об =  = 50,95 Нм — відповідь вірна.

5.4 ФАКТОРИ ЯКІ ВПЛИВАЮТЬ НА КОЕФІЦІЄНТ КОРИСНОЇ ДІЇ

        Коефіцієнт корисної дії завжди менший 100%, тобто η < 1. Загалом ККД- це показник досконалості машини, механізму чи привода.

На значення ККД впливають такі фактори:

1.  Конструкція механізму: черв'ячний, зубчастий, пасовий, ланцюговий, фрикційний і т. ін. Наприклад, на ККД черв'ячного редуктора впливає число заходів різьби на черв'ячному гвинті; на ККД зубчастих редукторів впливає конструктивне оформлення - закритий механізм у герметичному корпусі із постійним змащенням чи відкрита конструкція; на ККД пасової передачі впливає вид пасу - плоский, клиновий чи зубчастий.

2.  Матеріали деталей, що працюють у парі. Наприклад: сталь і сталь (зубчасті передачі); сталь і бронза або сталь і чавун (черв'ячні передачі); сталь і гума (фрикційні або пасові механізми) і т. ін. Є антифрикційні пари матеріалів, при застосуванні яких втрати корисної енергії менші - це такі матеріали: сталь з бронзою або сталь із чавуном.

3.  Поверхнева твердість матеріалів деталей: чим твердіша поверхня, тим втрати на тертя менші, а ККД більший.

4.  Спосіб переміщення деталей - ковзанням чи коченням: при ковзанні витрати на подолання сил опору руху (або сил тертя) на багато більші, ніж при коченні.

5.  Шорсткість поверхонь деталей ( поверхні можуть бути поліровані, шліфовані, грубо обточені і т. ін.). Чим більш гладенькі поверхні, тим менші витрати на подолання сил тертя, а ККД більший.

6.  Наявність мастила між поверхнями деталей або його відсутність, кількість мастила, його густина: це може бути рідке масло, мазь, тверді мазі різних видів. Якщо металеві поверхні зовсім не дотикаються одна до одної - режим тертя називається рідинним; якщо мастило відсутнє - режим тертя називається сухим.

При застосуванні змащування ККД механізму завжди більший.

         

Прикладом найбільш досконалого виробу є підшипники кочення, тому що для кілець, шариків та роликів застосовуються спеціальні сталі, поверхні цих деталей дуже тверді, вид переміщення деталей - кочення, застосовується спеціальна пластична мазь, підшипники працюють у герметичних конструкціях. Їх ККД η = 0,995.

           Приклади ККД деяких поширених механізмів:

Закриті зубчасті редуктори	η = 0,97
Відкриті зубчасті редуктори	η = 0,95
Закриті черв'ячні редуктори	η = 0,75 (при Z1 = 1)
	η = 0,85 (при Z1 = 2)
	η = 0,95 (при Z1 = 4)
Відкрита ланцюгова передача	η = 0,90
Клинопасова передача	η - 0,96
Металообробні верстати	η - 0,80

 

5.5 СИЛИ ІНЕРЦІЇ

Сили інерції - так називають динамічні сили, які виникають завжди при русі тіла з прискоренням. Сили інерції визначаються за формулою:

F_ІН = – m·a

Знак « – » показує, що вектор сили інерції F_ін завжди спрямований в бік,

протилежний вектору прискорення a .

Сили інерції мають різні якості: вони можуть проявлятись як небезпечні і руйнівні, або їх використовують в конструкціях спеціальних приладів, або їх треба просто враховувати з метою безпеки життєдіяльності.

Сили інерції сприяють розриву ланцюгів, тросів, дротин, руйнації абразивних кругів, лопаток парових турбін, маховиків, проявляються при різкому гальмуванні транспорту або при стрімкому зрушенню транспорту з місця, при старті космічного корабля (тоді космонавти відчувають величезне перевантаження), при русі на каруселях і на «американських гірках». Сили інерції використовуються в сепараторах, центрифугах, регуляторах, відцентрових муфтах, їх враховують спортсмени і актори цирку при виконанні деяких трюків, пілоти літаків при виконанні «фігур вищого пілотажу», водії швидкісних спортивних машин. Розглянемо кілька прикладів:

1.              Сила інерції при прискореному горизонтальному русі тіла: при стрімкому зрушенню тіла всі вільні предмети переміщуються назад (в потягу, в трамваї). Тому в транспорті треба завжди треба триматися за спеціальні ручки.

 

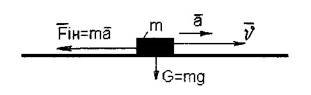
2.              Сила інерції при вертикальному прискореному русі тіла вниз (наприклад, в кабіні ліфта): при рівності прискорень а = g = 9,81 м/с² (тобто вільному падінні тіла) настає «стан невагомості», коли важке тіло не показує на терезах своєї ваги, бо не тисне на пружину в конструкції терезів, тому що G = F_ін, а їх вектори спрямовані протилежно.

 

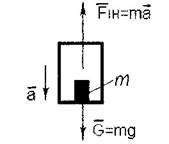
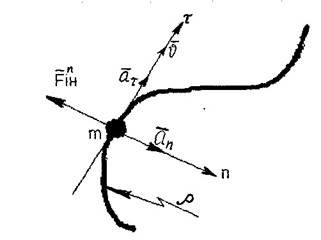
3.              Сила інерції при криволінійному русі тіла (машини на складній трасі, вагончики на «американських гірках»). В цьому випадку сила інерції

називається відцентровою силою інерції F_інⁿ , спрямованою протилежно

v2                   n                      v2 доцентровому прискоренню           m  a _n . Величина a _n          , тоді F_ін  m        , де ρ -

                                                                                    інn                                                                                                                             

змінний радіус кривизни траєкторії.

 

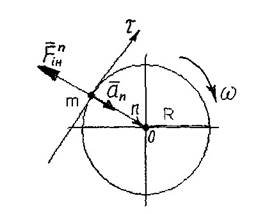
4.              Сила інерції при обертальному русі тіла (каруселі, маховики, абразивні круги, лопатки турбін, зубчасті колеса, ротори двигунів, гвинти).

                  Відцентрова сила інерції при обертальному русі обчислюється теж за

формулою: F_інⁿ  m a_n .

Але тут доцентрове прискорення а_п = ω^г · R, тому F_інⁿ  m _²  R . Ця сила пропорційна квадрату кутової швидкості ω і може бути дуже великою. Тому всі тіла обертання - зубчасті колеса, шківи, вали, ротори, турбіни, фрези, підшипники кочення розміщують в закритих герметичних корпусах, а при роботі із шліфувальними та абразивними кругами треба користуватись захисними щитами і захисними окулярами.