ТЕХНІЧНА МЕХАНІКА. Методичні вказівки до виконання самостійних практичних робіт студентами всіх технічних спеціальностей денної та заочної форми навчання
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ЗАПОРІЗЬКИЙ ЕЛЕКТРОТЕХНІЧНИЙ ФАХОВИЙ КОЛЕДЖ
НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ «ЗАПОРІЗЬКА ПОЛІТЕХНІКА»
ЗАТВЕРДЖЕНО
Протокол засідання
ЦК 133 Галузеве машинобудування від «____»___________201 р.№___
ТЕХНІЧНА МЕХАНІКА
Методичні вказівки до виконання самостійних практичних робіт
студентами всіх технічних спеціальностей денної та заочної форми навчання
Викладач І.В. Дубовський
2020
Збірник методичних вказівок до виконання самостійних робіт з предмета «Технічна механіка» для студентів всіх технічних спеціальностей денної та заочної форми навчання, розглянуто на засіданні методичної ради коледжу та рекомендовано для використання у навчальному процесі.
Секретар методичної ради В.В. Кузьмєнкова
Передмова
Методичні вказівки призначені для студентів всіх технічних спеціальностей коледжу. Їх метою є допомога студентам .у виконанні практичних і самостійних завдань з блоків «Теоретична механіка» та «Опір матеріалів». Теми самостійних робіт відповідають навчальним програмам спеціальностям де викладається дисципліна «Технічна механіка» та «Механіка».
Умови завдань до кожної самостійної роботи студенти отримують після вивчення відповідної теми на занятті -- у відповідності з постійним номером варіанта студента (за списком у навчальному журналі групи).
При виконанні завдань до самостійної роботи слід використовувати рекомендовану навчальну літературу.
Виконані студентом завдання оцінюються за п’ятибальною шкалою: «5», «4», «3», «2». При оцінюванні робіт враховується правильність і точність результатів обчислення, охайність оформлення, своєчасність виконання роботи, правильність відповідей на контрольні питання у відповідності до теми самостійної роботи.
Проекції сил на осі координат Х та У............................................................. 6
Визначення реакцій в шарнірних опорах балки............................................ 17
Визначення центра ваги складного перерізу................................................ 22
Вступ
Технічна механіка – це інженерна прикладна наука, яка складається із трьох окремих, але взаємно пов’язаних предметів: теоретичної механіки, опору матеріалів та деталей машин.
Теоретична механіка – це наука про закони механічного руху твердих тіл та умови рівноваги твердих тіл під дією прикладених до них зовнішніх сил та систем сил.
Опір матеріалів – це наука про методи розрахунків різних деталей машин, механізмів, пристроїв, а також елементів конструкцій і споруд на міцність, жорсткість, стійкість і витривалість. Мета розрахунків – отримати ще на стадії проектування будь-якого виробу гарантію, що він буде міцний, надійний і матеріало ємкий.
Деталі машин – це наука про склад та принцип роботи найбільш поширених в машинобудуванні механізмів, про види роз’ємних та нероз’ємних з’єднань, про стандартні вузли та деталі. В деталях машин вивчають основи проектноконструкторської роботи, спираючись на набуті знання і навички при вивченні таких предметів як теоретична механіка, опір матеріалів, інженерна графіка, технологія конструкційних матеріалів, взаємозамінність, стандартизація та керування якістю, математика.
Теоретичні знання повинні бути закріплені шляхом виконання студентами самостійних робіт з кожного блоку або модуля предмету. Теми завдань до самостійних робіт відповідають робочим навчальним програмам всіх технічних спеціальностей коледжу.
При виконанні самостійної роботи №1 студенти набувають вмінь знаходити проекції векторів сил на осі координат X та Y; при виконанні самостійної роботи №2 студенти набувають вмінь знаходити моменти сил відносно точок: ці вміння необхідні при розв’язку багатьох задач теоретичної механіки та опору матеріалів.
При виконанні самостійної роботи №3 студенти закріплюють знання про реакції зв’язків та аналітичний спосіб їх визначення з допомогою систем рівнянь рівноваги статики – це знадобиться при рішенні задач в опорі матеріалів та при розрахунках підшипників на довговічність.
При виконанні самостійної роботи №4 студенти знайомляться з геометричними характеристиками перерізів, щоб згодом використати набуті знання та вміння при розрахунках деталей з різними поперечними перерізами на міцність в опорі матеріалів.
При виконанні самостійної роботи №5 студенти засвоюють методи розрахунків простих виробів у формі бруса на розтяг та стиск, набувають практичних навичок визначати небезпечну ділянку стержня формулювати висновки про міцність та жорсткість стержня.
При виконанні самостійної роботи №6 студенти засвоюють поширений в опорі матеріалів і деталях машин проектний вид розрахунків розмірів простих деталей із умов міцності: наприклад валу редуктора із умови міцності на кручення і зображення його ескізу згідно отриманим розмірам.
Самостійна робота №1
1 Тема
Проекції сил на осі координат Х та У.
2 Мета
Навчитися визначати проекції векторів сил на осі координат Х та У для застосування набутих вмінь при рішенні задач з технічної механіки.
3 Інформаційне забезпечення
Теоретичні відомості [1....5]
4 Методичні вказівки
Познайомитись з правилами знаходження проекцій векторів сил на осі Х та У, використовуючи знання із математики та інженерної графіки :
___
–проекцією сили F на вісь називається відрізок на осі Х або У, що лежить між двома перпендикулярами, опущеними на вісь з початку і кінця вектора сили
___
F . Проекції сил дорівнюють катетам прямокутного трикутника ( рис. 1). Позначаються проекції Fx або Fy;
– проекція сили на вісь – величина алгебраїчна: може бути додатною або від’ємною (рис. 1 та рис. 2);
– проекція сили – величина скалярна (просто відрізок);
– правило знаків: якщо напрям проекції збігається з додатним напрямом осі Х (вправо) або У (вліво), то ця проекція буде додатною, і навпаки
(див. рис.1 та рис.2);
– проекція сили, перпендикулярної до осі Х або У дорівнює нулю (рис.3 та рис. 4)
– проекція сили паралельної до осі дорівнює натуральній величині сили – із знаком „плюс” або „мінус” (рис. 5 та рис. 6)
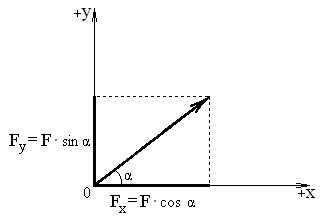
Рисунок 1 – Додатні проекція сили F
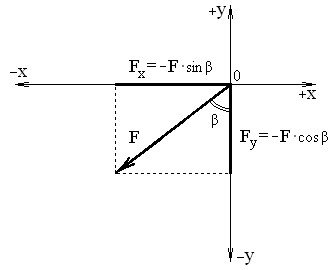
Рисунок 2 – Від’ємні проекції сили
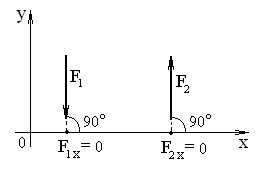
Рисунок 3 – Проекції сил F1 та F2, перпендикулярних до осі Х
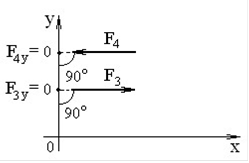
Рисунок 4 – Проекції сил F3 та F4, перпендикулярних до осі У
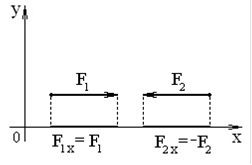
Рисунок 5 – Проекції сил F1 та F2, паралельних до осі Х
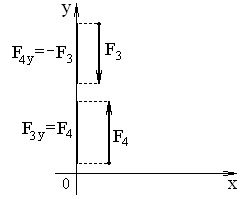
Рисунок 6 – Проекції сил F3 та F4, паралельних до осі У
– Залежно від напряму вектора сили одна проекція сили може бути додатною, а друга – від’ємною (див. 7):
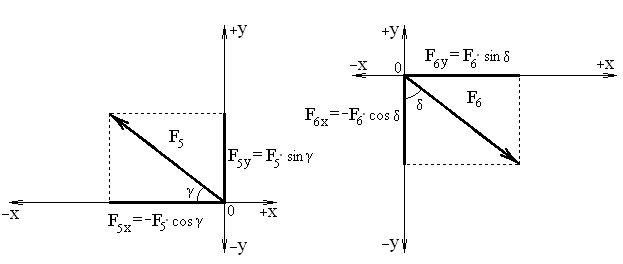
Рисунок 7 – Проекції похилих сил F5 та F6 на осі Х та У
Примітка – катет (проекція сили), прилеглий до кута ά ( чи β, чи γ, чи δ) дорівнює добутку гіпотенузи (модуля сили) трикутника на косинус (cos) цього кута; катет (проекція сили) ,протилеглий відносно кута ά ( чи β, чи γ, чи δ) дорівнює добутку гіпотенузи (модуля сили) трикутника на синус (sin) цього кута.
5 Приклад розв’язку завдання до самостійної роботи №1.
Виконати самостійну роботу : знайти проекції зображених векторів сил F1,, F2, F3 на осі Х та У (рис. 8); визначити алгебраїчні суми однойменних проекцій на осі координат Х та У.
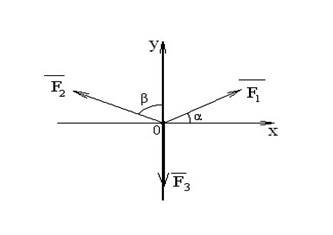
Дано:
F1 = 50H;
F2 = 100H; F3 = 40H; α = 350;
β= 700.
Рисунок 8 – Приклад умови завдання до самостійної роботи №1
Визначити : F1х, F1у, F2х, F2у, F3х, F3у.
Розв’язок
Проекції сил на осі Х та У:
F1х = F1 · cos α = F1 · cos 350 = 50 · 0,819 = 40,96H
F1у = F1 · sin β = F1 · sin 350 = 50 · 0,5736 = 28,68H
F2х = -F2 · sin β = -100 · sin700 = -100 · 0,94 = -94H
F2у = F2 · cos = 100 · cos700 = 100 0,342 = 34,2H
F3х = 0
F3у = - F3 = -40H
Алгебраїчні суми однойменних проекцій сил окремо на осі Х та У :
п
Fix = F1х + F2х+ F3х =40,96 – 94 = -53,04H;
i1 п
Fiy = F1у + F2у+ F3у= 28,68 + 34,2 – 40 = 22,88H.
i1
Результат (контрольні відповіді):
Fix = -53,04H.
Fiy = 22,88H.
6 Завдання до СР №1
Умови завдань до СР №1 (рис. 9) видаються викладачем студентам на
занятті після вивчення даної теми згідно постійному номеру варіанта студента.
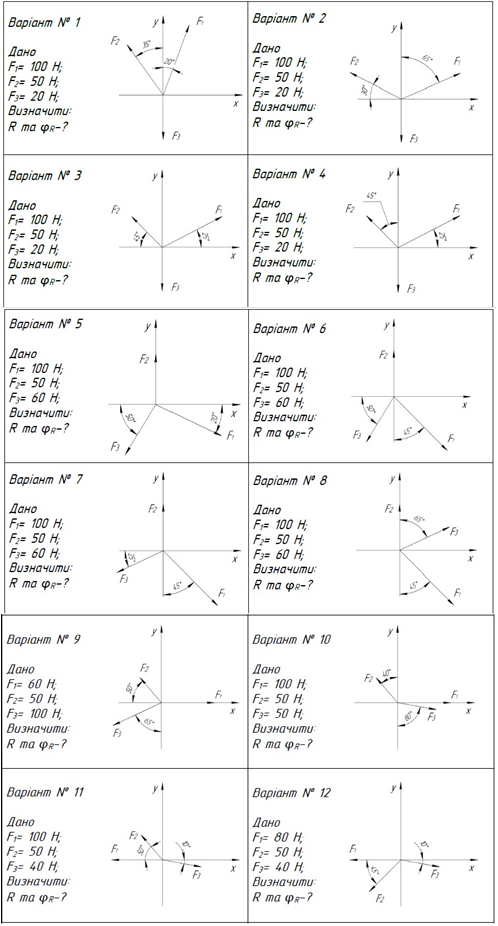
Рисунок 9.1 – Варіанти завдань до самостійної роботи № 1
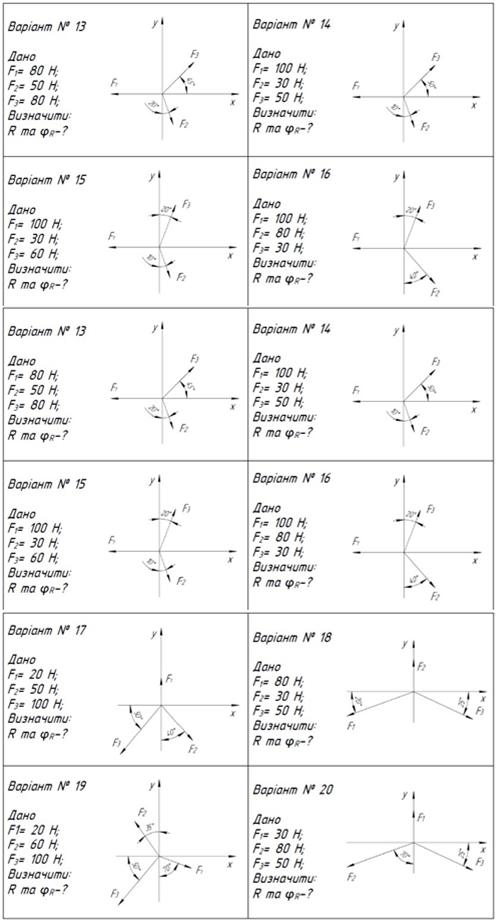
Рисунок 9.2 – Варіанти завдань до самостійної роботи № 1
7 Контрольні питання
7.1 Що називається проекцією сили на вісь?
7.2 В якому випадку проекція сили на вісь дорівнює нулю?
7.3 В якому випадку проекція сили на вісь дорівнює модулю сили?
7.4 В якому випадку проекція сили на вісь додатна?
7.5 В якому випадку проекція сили на вісь від’ємна?
Самостійна робота №2
1 Тема
Моменти сил відносно точок
2 Мета
Навчитись визначати моменти сил відносно будь – яких точок для застосування набутих вмінь при рішенні задач з технічної механіки.
3 Інформаційне забезпечення
Теоретичні відомості [1....5]
4 Методичні вказівки
Познайомитись з правилами знаходження моменту сил довільно спрямованої сили відносно будь – якої точки :
– моментом сили F,H відносно точки О ( або А, В, С, і т. ін.) називається добуток модуля сили на її плече h,м ; Позначають момент так : Мо=±F·h, H·м;
– момент М може бути додатнім, від'ємним або дорівнювати нулю;
– момент М характеризує обертальну дію сили на тверде тіло;
– точка, відносно якої знаходять моменти сили називається центром
моменту сили ( точки О, А, В, С, і т. ін.);
– плечем h сили відносно точки О називають найкоротшу відстань від центра момента до лінії дії даної сили : плече h сили дорівнює довжині перпендикуляра, опущеного із центра момента О на лінію дії сили (рис. 10);
– момент вважається додатнім, якщо сила намагається обертати тверде тіло навколо центра момента за годинниковою стрілкою (рис. 11);
– момент вважається від'ємним, якщо сила намагається обертати тверде тіло проти ходу годинникової стрілки (рис. 12);
– якщо точка (центр момента) лежить на лінії дії даної сили, момент такої сили дорівнює нулю, оскільки плече h ( довжина перпендикуляра в цьому випадку) дорівнює нулю (рис. 13); в цьому випадку тіло не може здійснювати обертальний рух.
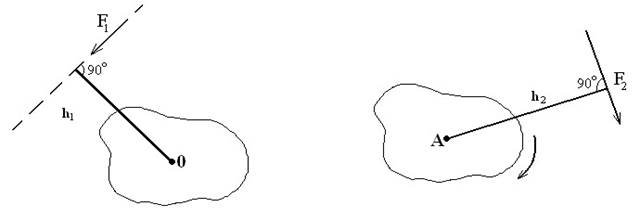
Рисунок 10 – Плече h1 – це перпен- Рисунок 11 – Сила F2 обертає тверде дикуляр із точки О на лінію дії. тіло за годинниковою стрілкою навколо. сили F1 точки А
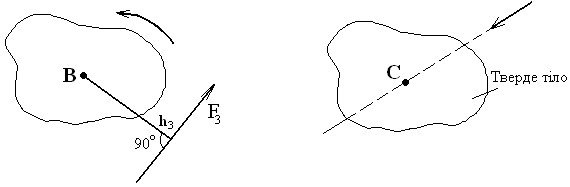
Рисунок 12 – Сила F3 обертає Рисунок 13 – Плече F4 відсутнє - тверде тіло проти годинникової тіло не обертається навколо точки С. стрілки навколо точки B.
Примітка: перпендикуляр із точки на лінію дії сили треба опускати з допомогою прямокутного трикутника.
5 Приклади визначення моментів сил F1, F2 , F3 , F4 , F5 , F6 відносно точок О,
А, В, С, D, К (рис. 14)
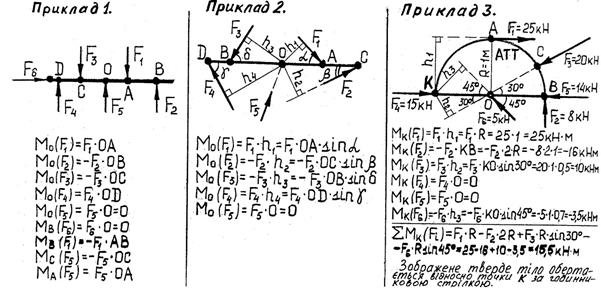
Рисунок 14-Приклади для закріплення вмінь знаходження моментів сил відносно точок
6 Приклад розв'язку завдання до самостійної роботи №2
Виконати самостійну роботу: визначити моменти сил F1, F2 , F3, прикладених до твердого тіла заданої форми відносно точки О (рис. 15); визначити алгебраїчну суму моментів всіх сил відносно центра обертання тіла точки О; вказати напрям обертання зображеного тіла.
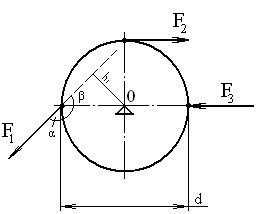Дано: F1 = 100Н;
F2 = 25Н; F3 = 33Н; d = 0,4 м; α = 135.0
Рисунок 15 – Приклад умови завдання до самостійної роботи №2
Розв'язок
Моменти сил F1, F2 , F3 відносно точки О:
Мо (F1) = - F1 · h1 = - F1 · d/2 · sinβ = - 100 · 0,4/2 · sin45° = - 14,14 Н·м;
Мо (F2) = F2 · d/2 = 25 · 0,4/2 = 5 Н·м; Мо (F3) = 0.
Алгебраїчна сума моментів сил відносно точки О:
п
Мо(Fі) = Мо (F1) + Мо (F2) + Мо (F3) = - 14,14+5 = - 9,14 Н·м.
i1
Висновок
Розрахунок вказує, що під дією сил F1, F2 , F3 тверде тіло обертається проти годинникової стрілки, тому що результуючий момент має від'ємне значення.
Примітка: величина кута β=45° визначена у відповідності з рисунком до задачі; значення sin α чи sinβ при розрахунках слід підставляти з точністю до 0,0001.
7 Завдання до СР №2
Умови завдань до СР №2 видаються викладачем на занятті після вивчення даної теми згідно постійному номеру варіанта студента.
8 Контрольні питання
8.1 Що називається моментом сили відносно точки?
8.2 В якому випадку момент сили відносно точки має додатній знак?
8.3 В якому випадку момент сили відносно точки дорівнює нулю?
8.4 Що ви знаєте про важіль та умову рівноваги важеля?
8.5 В яких випадках в техніці та в побуті можна використати знання про момент сили відносно точки?
Самостійна робота № 3
1 Тема
Визначення реакцій в шарнірних опорах балки
2 Мета
Навчитись складати рівняння рівноваги статики з метою визначення реакцій в шарнірних опорах балки
3 Інформаційне забезпечення
Теоретичні відомості [1…5]
4 Методичні вказівки
Загальні відомості
В інженерних розрахунках часто зустрічаються задачі, в процесі розв’язку яких необхідно визначити реакції різних зв’язків (площин, гнучких зв’язків, жорстких стержнів), в тому числі і шарнірних опор балок. Балка – так в інженерних розрахунках узагальнено називають всі довгі і тонкі вироби, деталі або елементи конструкцій, які можуть згинатись під дією зовнішніх сил. Кінці балки повинні бути закріплені для забезпечення рівноваги балки: вали верстатів, машин, редукторів, осі вагонів закріплюються за допомогою підшипників кочення, які відносяться до групи зв’язків, що називаються шарнірні опори. Консольними називають балки, в яких закріплений тільки один кінець: таке закріплення називають жорстке затиснення, наприклад різець у верстаті, балкони у стіні будинку, пластинчаста контактна пружина у вимикачі.
В шарнірних опорах і жорсткому затиснені виникають реактивні сили або просто реакції, які зрівноважують дію зовнішніх сил і пар сил, прикладених до балки. Кількість реакцій і їх напрям залежить від напряму зовнішніх навантажень: зовнішні сили можуть бути похилими або вертикальними, пари сил можуть бути з додатним моментом або від’ємним. Для розв’язку задач на визначення реакцій спочатку треба засвоїти правила із попередніх тем модуля «Статика» і застосувати знання із математики:
- навчитись знаходити проекції векторів сил на осі координат Х та У;
- навчитись знаходити моменти сил відносно точок;
- навчитись складати рівняння рівноваги статики: алгебраїчні суми моментів відносно шарнірних опор балки або жорсткого затиснення консольної балки, та алгебраїчні суми проекцій на осі Х та У;
- згадати із математики правила розв’язку системи рівнянь із двома або трьома невідомими реакціями;
- застосувати вміння правильно обчислювати невідомі величини з допомогою калькуляторів.
Системи рівнянь рівноваги статики на плоску систему довільно розміщених сил поділяються на дві групи:
І (основна) ІІ
1.Fix 0 1.M A Fi 0
2.Fiy 0 2.M B Fi 0
3.M A (Fi ) 0 3. Fiy 0
Першу групу рівнянь складають, якщо на розрахунковій схемі балки є хоча б один похилий вектор сили. Другу групу рівнянь складають, якщо до балки прикладені тільки вертикальні сили.
5 Задачі на визначення в реакцій шарнірних опорах балки вирішуються в такій послідовності:
5.1На рисунку до задачі позначають шарнірні опори буквами А та В.
5.2Показують в опорах реакції: вертикально вгору YA та YB , горизонтально X A (або X B ) вправо із центра шарнірів.
5.3Складають систему трьох рівнянь рівноваги статики І та ІІ групи.
5.4Розв’язок кожного рівняння виконують спочатку в загальному вигляді – алгебраїчно.
5.5Величини реакцій обчислюються з точністю до 0,01.
5.6З метою перевірки правильності розв’язку задачі складають додаткове рівняння, яке при правильному обчисленні реакцій повинне перетворитись в тотожність нулю.
Примітки:
- якщо до балки прикладені тільки вертикально спрямовані зовнішні сили
F1 та F2 – горизонтальні реакції в шарнірно-нерухомій опорі X A (або X B ) дорівнюють нулю;
- задані моменти М входять до складу рівнянь моментів із своїм знаком згідно рисунку до задачі;
- задані моменти М відсутні в рівняннях проекцій сил на осі х або у
(моменти на осі не проектуються);
- якщо реакція YA або YB після розв’язку рівнянь вийде від’ємною – це вказує, що вектор такої реакції фактично спрямований вниз (це не є помилкою);
- числові значення реакцій в шарнірних опорах балки впливають на вибір типу і розмірів підшипників кочення при проектуванні машин і механізмів.
6 Приклад розв’язку задачі до самостійної роботи № 3
6.1 Завдання: визначити реакції в шарнірних опорах зображеної балки, навантаженої силами F1 та F2 і парою сил з моментом М. Вагою балки знехтувати.
Дано:
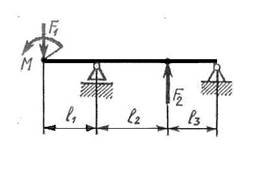M = 18 кН*м;
F1 = 55 кН; F2 = 22 кН; l1 = 1 м; l2 = 1,3 м; l3 = 0,7 м.
Рисунок 3.1 – Умова задачі до прикладу 6.1
Розв’язок задачі
6.1.1 Шарнірні опори: ліва А, права В.
6.1.2 Реакції в опорах: в лівій шарнірно-рухомій одна YA, в правій шарнірнонерухомій дві - X B та YB .
6.1.3 Розрахункова схема сил задачі має вид (рис. 3.2)
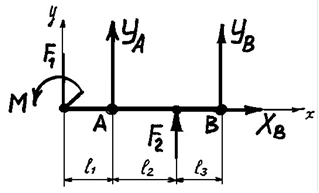
Рисунок 3.2 – Розрахункова схема сил до задачі
6.1.4 Система трьох рівнянь рівноваги ІІ групи у відповідності з рис.3.2:
M A 0; M F1 l1 F 2l2 YB l2 l3 0
M B 0; M F1l1 l2 l3 Y A l2 l3 F2 l3 0
F 0; F1 Y A F2 YB 0 iy
6.1.5 Алгебраїчне рішення рівнянь моментів в загальному вигляді відносно невідомих реакцій YA та YB :
Y A M F1 l1 F2 l 2 ; YB M F1 l1 l 2 l 3 F2 l 3 ;
l 2 l 3 l 2 l 3
6.1.6 Обчислення величин реакцій YB та YA, кН:
18 55 1 22 1,3
YB 
50,8 ;
1,3 0,7
YB 
83.8 .
Реакція X B = 0.
6.1.7 Перевірна правильності визначених реакцій згідно третьому рівнянню рівноваги:
Fiy 55 83.8 22 50.8 105 .8 105 .8 0
6.1.8 Висновок: перевірне рівняння перетворилось в тотожність нулю – значить реакції YA та YB визначені вірно: YA=83,8 кН; YB =-50,8 кН.
7 Приклади кількох варіантів завдань до самостійної роботи №3 (рис. 3.3, табл. 3.1).
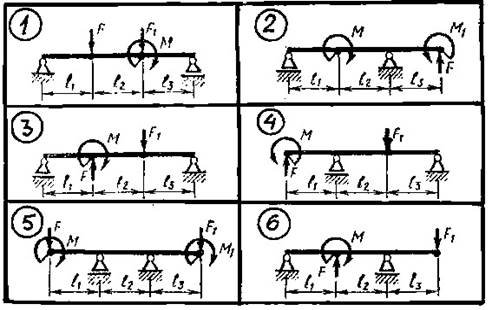
Рисунок 3.3 – Варіанти завдань до СР №3
Таблиця 3.1 – Числові значення величин до завдань СР №3 згідно рис. 3.3
|
Номер варіанту задачі |
F |
|
|
F1 |
M |
|
M1 |
l1 |
l2 |
l3 |
|
|
кН |
|
|
кНм |
|
м |
|
|||
|
1 |
11 |
|
|
10 |
5 |
|
- |
0.5 |
1.5 |
2 |
|
2 |
22 |
|
|
- |
7 |
|
10 |
0.6 |
1.4 |
1.2 |
|
3 |
33 |
|
|
30 |
9 |
|
- |
0.7 |
1.3 |
1.4 |
|
4 |
44 |
|
|
40 |
11 |
|
- |
0.8 |
1.2 |
1.6 |
|
5 |
45 |
|
|
50 |
13 |
|
16 |
0.9 |
1.1 |
1.8 |
|
6 |
46 |
|
|
60 |
15 |
|
- |
1 |
1 |
2 |
8 Контрольні питання
8.1 Які вироби в механіці називаються балками?
8.2 Які реакції виникають в шарнірних опорах балки – показати на рисунку.
8.3 Які реакції виникають в жорсткому затисненні консольних балок, навантажених вертикальними і похилими зовнішніми силами?
8.4 Які системи рівнянь рівноваги треба скласти для визначення невідомих реакцій в шарнірних опорах та в жорсткому затисненні консольних балок?
8.5 Як можна перевірити правильність визначених реакцій в задачі?
Самостійна робота № 4
1 Тема
Визначення центра ваги складного перерізу
2 Мета
Навчитись визначати положення центра ваги складного перерізу із трьох стандартних прокатних профілів аналітичним способом.
3 Інформаційне забезпечення
Теоретичні відомості 1…6
4 Методичні вказівки
Загальні відомості
4.1 Центр ваги − це єдина точка в межах будь-якого твердого тіла, пластини або перерізу бруса, яка є центром його рівноваги. Знання про положення центра ваги в межах конструкції чи перерізу бруса враховуються при розрахунках в теоретичній механіці та в опорі матеріалів при розрахунках на міцність.
Положення центра ваги (позначається С) можна визначати двома способами − методом підвішування або аналітичним. Аналітичний спосіб полягає у визначенні координат точки С (Хc, Yc) за формулами, тобто є розрахунковим способом.
Примітки: при розв’язку задач на визначення координат центра ваги застосовуються такі методи:
- метод розбиття складного перерізу на прості складові частини, площі яких легко визначити за формулами математики;
- метод від’ємних площ: якщо згідно рисунку до задачі площу якоїсь частини вважати відсутньою, то у формулах ця площа має від’ємний знак.
Формули для обчислення координат Хc та Yc складних пластин або перерізів мають вид:
X C Ai xi A1x1 A2x2 A3x3 ;
Ai A1 A2 A3
A y A y A y A y YC i i 1 1 2 2 3 3 , Ai A1 A2 A3
де 1, 2, 3 − порядкові номери частин конструкції або складного перерізу, на
які їх розділяють для спрощення розрахунків;
А1, А2, А3 − площі перерізів цих частин які обчислюються за формулами математики для геометричних фігур або визначаються із таблиць сортаменту для прокатних профілів;
x1, x2, x3, − координати точок С1, С2, С3, позначених відповідно як центри
ваги кожної окремої частини 1, 2, 3 вздовж осі x;
y1, y2, y3 − координати точок С1, С2, С3, позначених відповідно як центри ваги
кожної окремої частини 1, 2, 3 вздовж осі y.
З метою прискорення рішення задач на визначення координат центра ваги та зменшення об’єму обчислень доречно знати такі властивості центра ваги:
- якщо пластина або твердо тіло має вісь симетрії або дві осі симетрії − центр ваги знаходиться на осі симетрії або в точці перетину осей симетрії, наприклад: круг, кільце, еліпс, куля, квадрат, куб, прямокутник, піраміда, ромб, двотавр, швелер, кутник рівнобічний тощо (рис. 4.1);
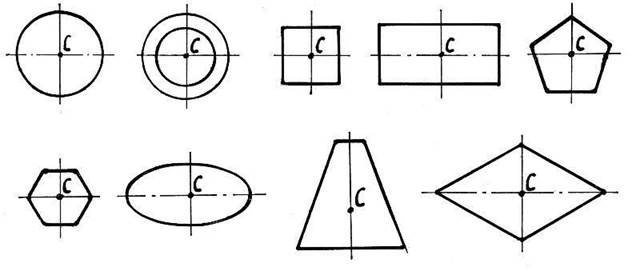
Рисунок 4.1 − Приклади форм пластин, які мають одну або дві осі симетрії
- центр ваги може не співпадати з матеріальною частиною тіла або пластини, наприклад: сфера, кільце, швелер, кутники (рис. 4.1);
- центр ваги займає незмінне положення в межах твердого тіла або пластини при будь-якому їх розташуванні у просторі − це дає змогу рисунок до задачі повертати в площині довільно, як зручніше (рис. 4.2).
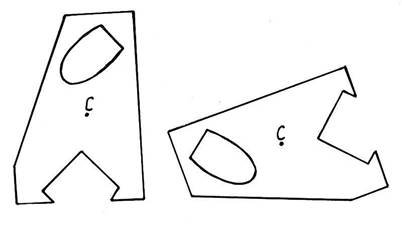
Рисунок 4.2 − Положення центра ваги пластини не залежить від її розташування у площині
4.2 Прокатні профілі − це продукція металургійних заводів, тобто фасонний металопрокат; форма поперечного прокату може бути різною, наприклад: у формі тавра, двотавра, швелера, кутників рівнобічних або нерівнобічних (рис. 4.3).
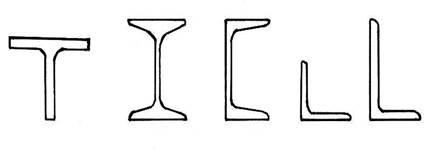
Рисунок 4.3 − Приклади форм поперечного перерізу металопрокату: тавр,
двотавр, швелер, кутник рівнобічний, кутник нерівнобічний
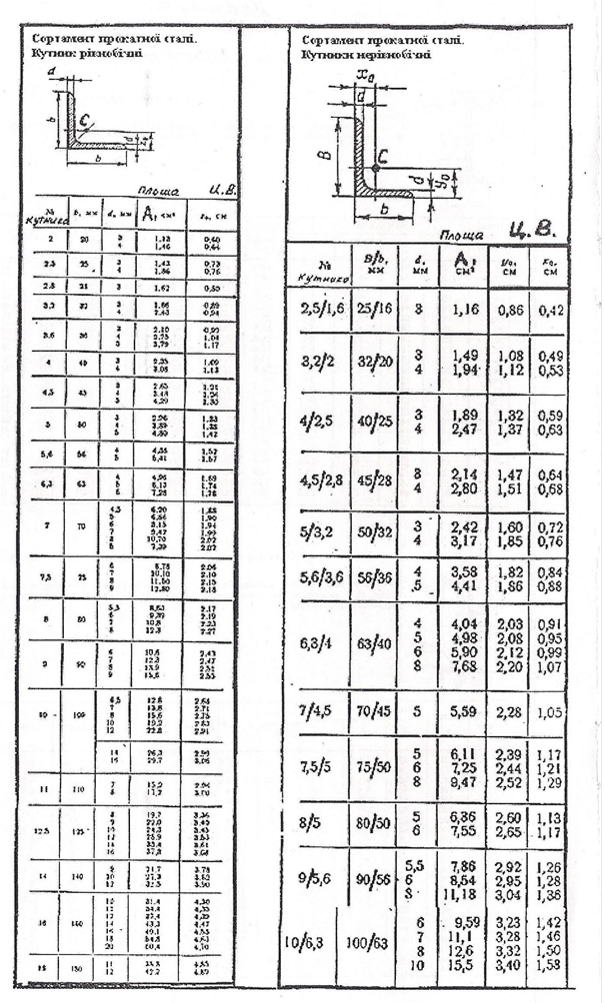
Вся інформація про кожний профіль знаходиться в спеціальних таблицях, які називаються таблицями сортаменту (див. додаток А): це маса одного погонного метра довжини профілю, розміри, площа поперечного перерізу та інші геометричні характеристики перерізу необхідні при розрахунках на міцність та на жорсткість силових конструкцій, виготовлених із кількох з’єднаних прокатних профілів. Розрахунки на міцність і на жорсткість вивчаються в опорі матеріалів, але починаються вони із визначення положення центра ваги поперечного перерізу аналітичним способом за формулами із теоретичної механіки.
Числові значення названих величин залежать від номера профілю, наприклад: двотавр № 10, швелер № 12, кутників рівнобічний № 7, кутник нерівнобічний № 8/5. Кожний прокатний профіль має деякі особливості; назви елементів профілів, їх позначення та інші пояснення суміщені із рисунками (рис.
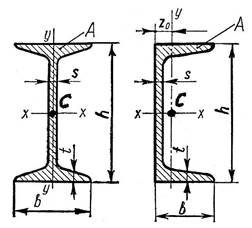4.4; 4.5; 4.6). h висота профілю; b ширина полички; s товщина стінки; t середня товщина полички;
A площа поперечного перерізу профіля; C центр ваги перерізу; xxyy осі симетрії двотавра;
xx вісь симетрії швелера;
Z0 координата точки С швелера.
Номер двотавра і номер швелера дорівнює висоті h (см).
Рисунок 4.4 Двотавр і швелер
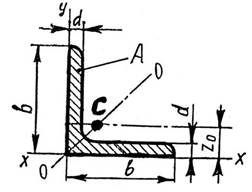b ширина полички; d товщина поличок;
A площа поперечного перерізу профіля;
C центр ваги перерізу;
ОО вісь симетрії кутника (бісектриса); Z0 координата точки С кутника.
Номер кутника це розмір полички b (см).
Рисунок 4.5 Кутник рівнобічний
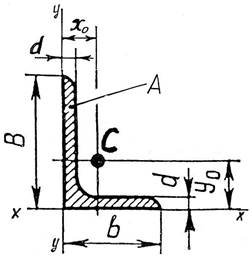В ширина більшої полички; b ширина меншої полички; d товщина поличок;
A площа поперечного перерізу профіля; C центр ваги перерізу; х0 та у0 координати точки С.
Номер кутника це дріб: 
B(см ) . b(см )
Рисунок 4.6 Кутник нерівнобічний
Завдання до самостійної роботи № 4 полягає у визначенні положення центра ваги (точки С) складного перерізу згідно варіанту завдання.
5 Послідовність рішення задачі до СР № 4
5.1 Перерисувати схематичне розташування трьох прокатних профілів згідно з варіантом завдання, виписати їх назви та номери.
5.2 Виписати із таблиць сортаменту розміри h, b, s, t, B, d, мм вказаних прокатних профілів; виписати площі їх поперечних перерізів А, см2 ; виписати координати їх центрів ваги Z0, x0, y0, см. Заповнити таблицю 4.1.
5.3 Виконати у масштабі 1:1 рисунок до задачі за розмірами із табл.. 4.1 на аркуші формату А4.
5.4 Присвоїти на рисунку порядкові номери 1, 2, 3 кожному профілю, відповідно позначити їх центри ваги С1, С2, С3, провести осі xoy так щоб рисунок був розташований у першій чверті.
5.5 Показати на рисунку координати точок С1, С2, С3 відповідно: x1y1, x2y2, x3y3; виміряти їх лінійкою в мм, перевести значення в см з точністю 0,01. Заповнити таблицю 4.2.
Таблиця 4.1 − Основні величини із таблиць сортаменту
|
Назви профілів та їх номери |
Основні розміри профілів, мм |
Площі перерізів профілів А, см2 |
Координати центрів ваги профілів, см |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблиця 4.2 − Результати обробки рисунка до задачі
|
Порядковий номер та назва профілю згідно рисунку |
Площі перерізів профілів А, см2 |
Координати центрів ваги профілів в системі xoy (в мм, потім в см) |
||
|
|
А1= |
С1 |
x1= |
y1= |
|
|
А2= |
С2 |
x2= |
y2= |
|
|
А3= |
С3 |
x3= |
y3= |
5.6 Обчислити координати загального центра ваги зображеного перерізу − точки С (Хc та Yc, см) з точністю 0,01:
X C Ai xi A1x1 A2x2 A3x3 ;
Ai A1 A2 A3
YC Ai yi A1y1 A2 y2 A3 y3 .
Ai A1 A2 A3
5.7 Побудувати точку С на рисунку до задачі за отриманими координатами (Хc;Yc).
5.8 З метою перевірки розв’язку задачі можна повернути рисунок на кут 900 або 1800, провести нові осі координат xoy, заново визначити координати точок С1, С2, С3, відповідно x1y1, x2y2, x3y3, заново обчислити величини Хc і Yc, побудувати точку С на рисунку. При правильному розв’язку задачі точки С і С співпадуть
5.9 Виписати результати обчислень.
6 Приклад розв’язку завдання до СР № 4
Визначити координати центра ваги зображеного перерізу із трьох стандартних прокатних профілів, схематичне розташування яких вказано у завданні згідно варіанту (рис. 4.7)
Швелер №14
Двотавр №10
Кутник № 6,3/4
Рисунок 4.7 − Схематичне зображення розташування трьох прокатних профілів згідно варіанту завдання
Таблиця 4.3 − Основні величини із таблиць сортаменту до рисунка 4.7
|
Назви профілів та їх номери |
Основні розміри профілів, мм |
Площі перерізів профілів А, см2 |
Координати центрів ваги профілів, см |
|
Швелер №14 |
h=140; b=58; s=4,9; t=8,1 |
15,6 |
Z0=1,67 |
|
Двотавр№ 10 |
h=100; b=55; s=4,5; t=7,2 |
12,0 |
− |
|
Кутник № 6,3/4 |
B=63; b=40; d=5 |
4,98 |
x0=0,95; y0=2,08 |
Виконати рисунок до задачі в масштабі 1:1 згідно розмірам із таблиці 4.3 (рис. 4.8). Показати на рисунку точки − центра ваги кожного профілю у відповідності до таблиці 4.3. Присвоїти на рисунку 4.8 порядкові номери кожному профілю 1, 2, 3 і відповідно центрам ваги − С1, С2, С3.
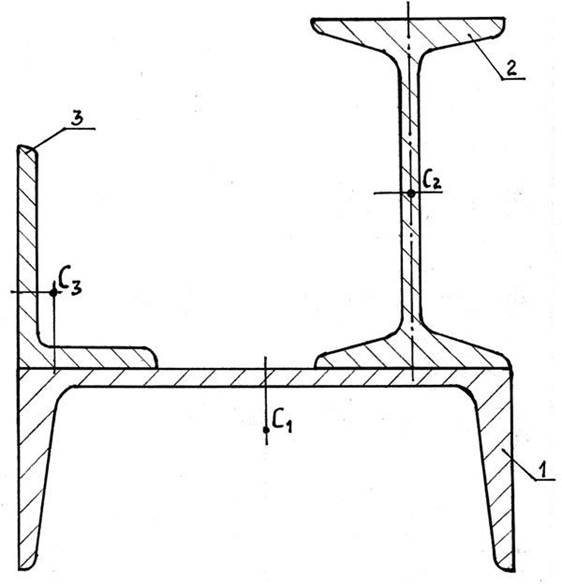
Рисунок 4.8 − Зображення рисунка згідно умові задачі та даним із табл. 4.3 Провести на рисунку 4.9 осі координат xoy так, щоб вони дотикались до контурів рисунка. Опустити із точок С1, С2, С3 перпендикуляри на осі x та y, виміряти лінійкою координати x1, x2, x3 та y1,y2,y3, мм (рис. 4.9), результати записати до табл. 4.4
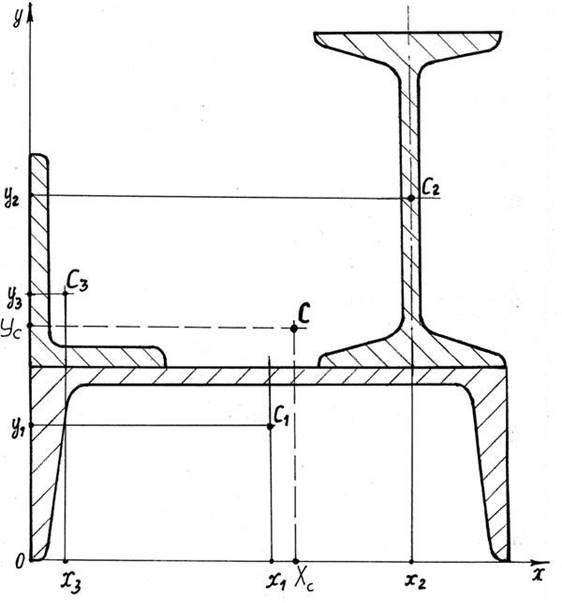
Рисунок 4.9 − Зображення осей координат xoy, координат точок С1, С2, С3, положення загального центра ваги перерізу точки С
Таблиця 4.4 − Результати обробки рисунка 4.9 до задачі
|
Порядковий номер та назва профілю згідно рисунку |
Площі перерізів профілів А, см2 |
Координати центрів ваги профілів в системі xoy (в мм, потім в см) |
||
|
1 швелер |
А1 = 15,6 |
С1 |
x1 = 70 = 7,0 |
y1 = 41 = 4,1 |
|
2 двотавр |
А2 = 12,0 |
С2 |
x2 = 114 = 11,4 |
y2 = 110 = 11 |
|
3 кутник |
А3 = 4,98 |
С3 |
x3 = 9,5 = 0,95 |
y3 = 80 = 8,0 |
Обчислити величини координат Хc та Yc, см точки С за формулами:
A x A x A x A x
X C i i 1 1 2 2 3 3 ; X C 15,6 7 12 11,4 4,98 0,95 7,7 ;
Ai A1 A2 A3 15,6 12 4,98
A y A y A y A y
YC i i 1 1 2 2 3 3 ; YC 15
,6 4,1 12 11 4,98 8 7,1 .
Ai A1 A2 A3 15,6 12 4,98
Побудувати точку С за отриманими координатами C (7,7; 7,1) на рис. 4.9 до задачі.
З метою перевірки рішення задачі повернемо рис. 4.9 на 900, заново проведемо координатні осі xoy (рис. 4.10), заново визначимо координати точок С1, С2, С3, відповідно x1y1, x2y2, x3y3, заново обчислимо величини Хc і Yc, та побудуємо точку С на рис. 4.10. При правильному розв’язку задачі точки С і С співпадуть.
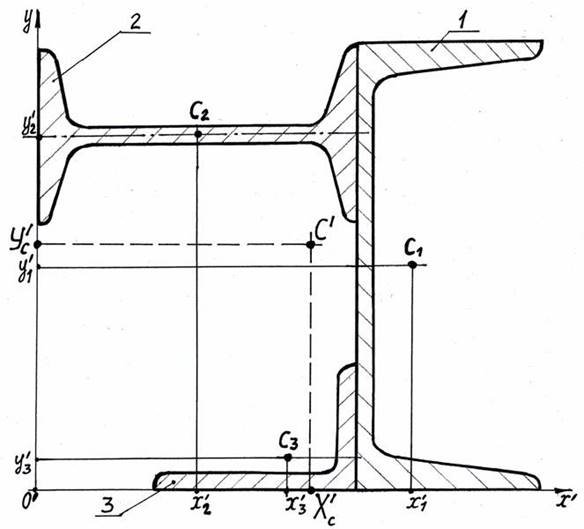
Рисунок 4.10 − Зображення рисунка до задачі в системі координат xoy, координат точок С1, С2, С3,положення загального центра
ваги перерізу точки С
X 'C 
8,7 ;
Y ' C 
7,7
Висновок
Точки С та Сспівпали положення центра ваги зображеного перерізу визначено правильно Результати:
Хc = 77 мм;
Yc = 71 мм.
7 Приклади кількох варіантів завдань СР № 4 (рис. 4.11, табл. 4.5)
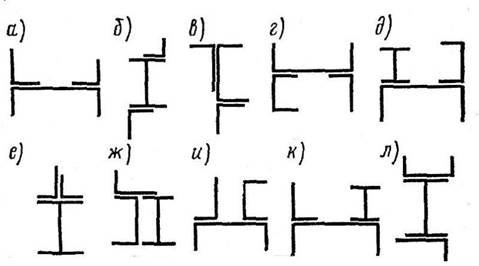
Рисунок 4.11 Схематичне розташування профілів до задач СР № 4
Таблиця 4.5 Номери профілів до задач згідно рис. 4.11
|
Номер варіанту |
Позначення рисунка |
Назви і номери профілів |
|||
|
двотавр |
швелер |
кутник рівнобічний |
кутник нерівнобічний |
||
|
1 |
а |
|
16 |
5 |
4,5/2,8 |
|
2 |
б |
10 |
|
3,2 |
4/2,5 |
|
3 |
в |
|
10 |
4 |
5/3,2 |
|
4 |
г |
|
5;14 |
|
6,3/4 |
|
5 |
д |
10 |
18;5 |
|
|
|
6 |
е |
14 |
|
2,8 |
5,6/3,6 |
|
7 |
ж |
12 |
12 |
|
10/6,3 |
|
8 |
и |
|
16;5 |
|
7/4,5 |
|
9 |
к |
10 |
14 |
|
6,3/4 |
|
10 |
л |
10 |
8 |
|
7,5/5 |
8 Контрольні питання
8.1 Що називається центром ваги твердого тіла або пластини?
8.2 Назвіть властивості центра ваги.
8.3 Назвіть методи знаходження положення центра ваги складної пластини або перерізу.
8.4 Назвіть основні елементи різних стандартних прокатних профілів.
8.5 Поясніть, як користуватись таблицями сортаменту.
8.6 Напишіть формули, за якими визначаються координати точки центра ваги пластини.
8.7 Поясніть послідовність розв’язку задачі до СР № 4.
8.8 В чому полягає сутність перевірки розв'язку задачі до СР № 4?
Самостійна робота № 5
1 Тема
Розрахунок ступінчастого стержня на міцність і жорсткість при розтягу і стиску
2 Мета
Навчитись розв’язувати задачі з опору матеріалів
3 Інформаційне забезпечення
Теоретичні відомості [1…6]
4 Методичні вказівки
Загальні відомості
Розрахунки на міцність полягають у визначенні величини найбільшої розрахункової напруги max в матеріалі виробу і порівняти max із заданою допустимою напругою [] у відповідності з умовою міцності при розтягу і стиску:
max N z / A
Якщо розрахункова напруга max не перевищує допустиму напругу [] – виріб (деталь) міцний; якщо max перевищує [] – виріб не міцний.
Розрахунки на жорсткість полягають у визначенні величини деформації стержня (деталі) ∆l за формулою Гука і порівнянні її величини з заданою допустимою величиною [∆l] згідно формулі:
N z l
l 
l, E A
де ∆l – абсолютна деформація стержня, мм;
Nz – внутрішня сила пружності (поздовжня або нормальна сила), H в поперечному перерізі стержня;
А – площа поперечного перерізу стержня, мм²;
Е – модуль поздовжньої пружності матеріалу стержня, МПа; l – початкова довжина заданого стержня, мм.
Величина і знак сили Nz, Н визначається в межах кожної ділянки стержня довжиною l на основі методу перерізу.
Величина площі А, мм² поперечного перерізу стержня визначається залежно від форми і розмірів поперечного перерізу (круглий, квадратний, кільцевий, прямокутний), або може бути задана в умові задачі.
Величина модуля пружності Е, МПа матеріалу стержня залежить від вказаного матеріалу (сталь, чавун, алюміній), може бути задана в умові задачі або визначається за довідником.
Величини допустимої напруги [], МПа та допустимої деформації [∆l],мм залежать від матеріалу виробу, від його деформації (розтяг чи стиск), від відповідальності деталі; їх значення часто вказані в умові до задачі: наприклад: [] = 160 МПа, [∆lзаг] = 0,1 мм.
5 Розрахунок стержня на міцність і жорсткість виконується у такій послідовності:
- позначити на рисунку характерні точки В, С, D, K, присвоїти порядкові номери силовим ділянкам стержня: 1-ВС, 2-СD, 3-DК.
- позначити згідно рисунку довжину l,мм кожної ділянки відповідно: ВС= l1, СD= l2, DК= l3;
- визначити в межах кожної ділянки величину поздовжньої сили Nz,H застосувавши метод перерізів; уточнити вид деформації кожної ділянки стержня;
- вибрати масштаб, побудувати епюру поздовжніх сил Nz по довжині стержня;
- визначити площу поперечного перерізу кожної ділянки стержня А, мм² згідно рисунку;
- визначити величини нормальних напружень в межах кожної ділянки за формулою: = Nz/А, МПа;
- вибрати масштаб, побудувати епюру нормальних напружень по довжині стержня;
- визначити величину найбільшої напруги згідно епюри напружень max ,
МПа порівняти цю величину із заданою допустимою напругою [], МПа;
- скласти відповідний висновок про міцність стержня;
- визначити величину деформації ∆l, мм кожної ділянки стержня за формулою Гука;
- визначити величину загальної деформації стержня ∆lзаг, мм як алгебраїчну суму деформацій усіх ділянок стержня;
- скласти висновок про характер деформації стержня – видовжився чи скоротився.
Примітки
- ступінчастими називають стержні, які мають різну товщину ділянок;
- епюри в опорі матеріалів – це спеціальні графіки, які будуються в проекції (внизу або праворуч) відносно рисунку до задачі для наочності і перевірки правильності розв’язку задач;
- при побудові епюр додатні значення сил Nz та напруг δ відкладаються вгору або праворуч від осі епюри як базової лінії, а від’ємні значення сил Nz та напруг – вниз або вліво (див. рис. 5.2 та рис. 5.3); масштаб вибирається довільно в межах кожної задачі – різний для епюри Nz і епюри ;
- загальна деформація ∆lзаг, мм визначається за формулою: ∆lзаг = ∑ lі якщо величина ∆lзаг вийде із знаком «плюс» стержень видовжується, якщо зі знаком «мінус» – стержень скорочується;
- якщо допустимо напруга не задана в умові задачі, її величину обчислюють за формулою: []=Т/[n] для пластичних матеріалів, або
[]=МЦ/[n] для крихких;
- модуль пружності матеріалу сталі = 200000 МПа = 2 10 5 МПа.
6 Приклади розв’язку задач до самостійної роботи № 5
6.1 Завдання: для зображеного двоступінчастого стержня (рис. 5.1) побудувати епюри поздовжніх сил і нормальних напруг по довжині стержня, скласти висновки про міцність стержня і характер його деформації. Матеріал стержня – сталь, допустиму напругу прийняти [] = 160 МПа.
F1 = 16 кН
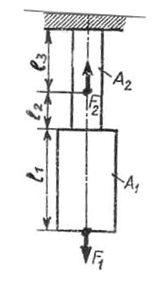F2 = 22 кН
A1 = 250 мм²
A2 = 180 мм² l1 = 110 мм l2 = 50 мм l3 = 80 мм
Е = 2 10 5 МПа.
[δ] = 160 МПа.
Рисунок 5.1 – Умова задачі до прикладу 6.1
Розв’язок задачі
6.1.1 Силові ділянки: І-ВС, ІІ-СD, ІІІ-DК (рис. 5.2)
6.1.2 Повздовжні сили: Nz1, Nz2, Nz3,кн. (рис. 5.2) і деформації ділянок стержня:
Ділянка ВС Nz1 = F1
Nz1 = 16 (деформація розтяг);
Ділянка СD Nz2 = F1
Nz2 = 16 (деформація розтяг);
Ділянка DК Nz3 = F1 – F2
Nz3 = 16 – 22 = – 6 (деформація стиск).
6.1.3 Масштаб епюри Nz: Мz 1 кН/мм (рис. 5.2)
6.1.4 Нормальні напруги , МПа
Ділянка ВС 1 
N Z 1
A1
16 10 3
1 
64 ;
250
Ділянка СD 2 
N Z 2
A2
16 10 3
2 
89 ;
180
Ділянка DК 3 N Z 3
A2
6 10 3
3 
33.3 .
180
6.1.5 Масштаб епюри : М 4 МПа/мм (рис. 5.2)
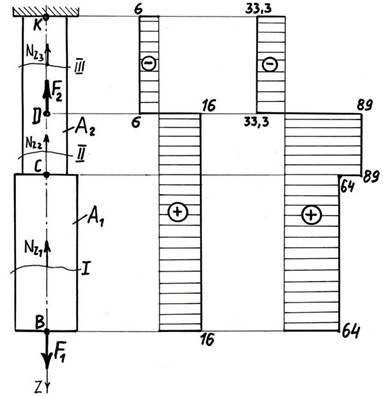
Рисунок 5.2 Силові ділянки стержня BC, CD, DK, поздовжні сили Nz1, Nz2, Nz3, епюра поздовжніх сил та епюра нормальних напруг по довжині стержня.
6.1.6 Величина найбільшої напруги мах = 89 МПа.
6.1.7 Порівняння мах із епюри напруг із допустимою напругою [] і висновок: 89 < 160 (тобто мах < [] ) – стержень міцний.
6.1.8 Деформація ділянок стержня, початкова довжина яких відповідно l1 ,
l2 , l3 ,мм (рис. 5.1)
Ділянка ВС l1 
N Z1 l1 E A1
16 10 3 110
l1 
5 0.0352 (видовження);
2 10 250
Ділянка СD l2 
N Z 2 l2 E A2
16 10 3 50
l 2 
5 0.0222 (видовження);
2 10 180
Ділянка DК l3 N Z 3 l3 E A2
6 10 3 80
l3 
5 0.0130 (скорочення).
2 10 180
6.1.9 Загальна деформація стержня ∆lзаг, мм і висновок:
∆lзаг = ∆l1 +∆l2 +∆l3
∆lзаг = 0,0352 + 0,0222 + 0,0130 = 0,0444 – стержень видовжився.
6.2 Завдання: для зображеного двостороннього стержня (рис. 5.3) побудувати епюри поздовжніх сил і нормальних напруг по довжині стержня, скласти висновки про міцність стержня і характер його деформації. Матеріал стержня сталь Ст.3, границя текучості якої Т = 240 МПа, допустимий коефіцієнт запасу міцності призначи [n] = 1,5.
F1 = 3 кН
F2 = 7.2 кН d = 8 мм a = 6 мм l1 = 350 мм l2 = 400 мм
Т = 240 МПа
[n] = 1,5
Е = 2 10 5 МПа.
Рисунок 5.3 – Умова задачі до прикладу 6.2
Розв’язок задачі
6.2.1 Силові ділянки: І-ВС, ІІ-СD (рис. 5.4)
6.2.2 Поздовжні сили: Nz1, Nz2, кн. (рис. 5.4) і деформація ділянок стержня:
Ділянка ВС Nz1 = F1
Nz1 = 3 (деформація розтяг);
Ділянка СD Nz2 = F1 – F2
Nz2 = 3 – 7,2 = – 4,2 (деформація стиск).
6.2.3 Масштаб епюри
6.2.3 Масштаб епюри Nz: М Nz 0,3 кН/мм (рис. 5.4)
6.2.4 Площі поперечних перерізів А,мм² ділянок стержня ВС, СD у відповідності із заданими в умові (рис. 5.3) формою і розмірами:
d 2
Ділянка ВС A1 Aкр 
4
3.14 8 2
A1 
50.24 4
Ділянка СD A2 Aкв а2
А2 62 36 .
6.2.5 Нормальні напруги , МПа
Ділянка ВС 1 N Z 1
A1
3 10 3
1 
59.7 ;
50.24
Ділянка СD 2 N Z 2
A2
N Z 2
2
A2
4.2 10 3
2 
116 .7 ;
36
6.2.6 Масштаб епюри : М 5 МПа/мм (рис. 5.4)
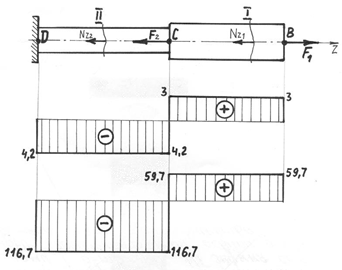
Рисунок 5.4 Силові ділянки стержня BC, CD, поздовжні сили Nz1, Nz2, епюра поздовжніх сил та епюра нормальних напружень по довжині стержня
6.2.7 Величина допустимої напруги [], МПа
[] = Т/[n]
[] = 240/1,5 = 160.
6.2.8 Порівняння мах із епюри напружень із допустимою напругою [] і висновок: 116,7 < 160 (тобто мах < [] ) – стержень міцний.
6.2.9 Деформація ділянок стержня, початкова довжина яких відповідно l1 та l2 ,мм (рис. 5.3)
Ділянка ВС l1 N Z1 l1 E A1
3 10 3 350
l1 
5 0.104 (видовження);
2 10 50.24
Ділянка СD l2 N Z 2 l2
E A2
N Z 2 l2
l2
E A2
4.2 10 3 400
l 2 
5 0.233 (скорочення).
2 10 36
6.2.10 Загальна деформація стержня ∆lзаг,мм і висновок:
∆lзаг = ∆l1 +∆l2
∆lзаг = 0,104 - 0,233 = - 0,129 – стержень скоротився.
7 Приклади кількох варіантів завдань до самостійної роботи № 5 (рис. 5.5, табл. 5.2)
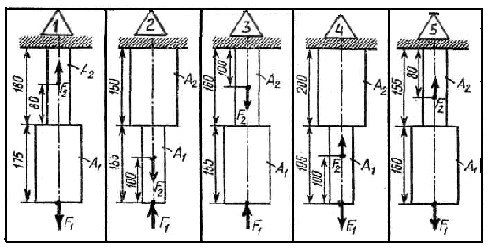
Рисунок 5.5 – Варіанти завдань до СР № 5
Таблиця 5.2 – Числові значення величин до завдань СР № 4 згідно рис. 5.5
|
Номер варіанту задачі |
F1 |
|
|
F2 |
А1 |
|
А2 |
Е1 |
[] |
|
|
кН |
|
кНм |
|
м |
|
|||
|
1 |
10 |
|
|
18 |
100 |
|
80 |
200000 |
160 |
|
2 |
20 |
|
|
35 |
200 |
|
150 |
200000 |
160 |
|
3 |
30 |
|
|
48 |
300 |
|
180 |
200000 |
160 |
|
4 |
40 |
|
|
55 |
400 |
|
500 |
200000 |
160 |
|
5 |
50 |
|
|
66 |
250 |
|
100 |
200000 |
160 |
8 Приклади кількох варіантів завдань до самостійної роботи № 5
(рис. 5.6 табл. 5.3)
Таблиця 5.3 – Числові значення величин до завдань СР № 4 згідно рис. 5.6
|
Номер варіанту задачі |
F1 |
F2 |
l1 |
l2 |
а |
а1 |
а2 |
d |
d1 |
d2 |
Е |
т |
[n] |
|
кН |
|
|
|
мм |
|
|
|
МПа |
|
||||
|
1 |
5 |
10 |
120 |
140 |
20 |
|
|
30 |
|
|
2105 |
280 |
1,4 |
|
2 |
4 |
3 |
100 |
150 |
15 |
|
|
20 |
|
|
2105 |
260 |
1,5 |
|
3 |
18 |
10 |
250 |
200 |
12 |
|
|
25 |
|
|
2105 |
300 |
1,8 |
|
4 |
22 |
40 |
150 |
180 |
25 |
|
|
15 |
|
|
2105 |
240 |
1,5 |
|
5 |
20 |
45 |
180 |
220 |
|
|
|
|
50 |
40 |
2105 |
300 |
2 |
|
6 |
6 |
16 |
80 |
100 |
|
30 |
20 |
|
|
|
2105 |
360 |
2 |
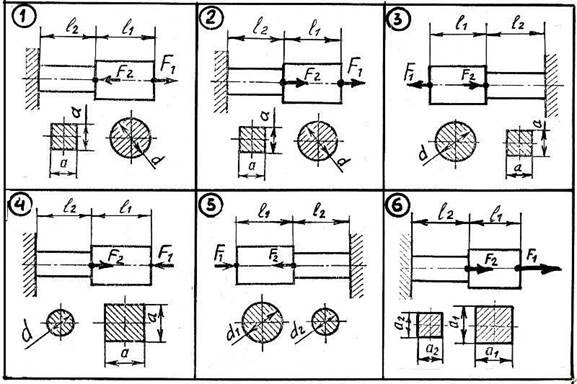
Рисунок 5.6 Варіанти завдань до СР № 5
9 Контрольні питання
9.1 Назвати фактори, які впливають на міцність і жорсткість будь-якого виробу або деталі?
9.2 За якою формулою обчислюються нормальні напруги при розтягу і стиску?
9.3 В якому випадку величини Nz, , ∆l мають додатні знаки, а в якому – від’ємні?
9.4 В чому полягає перевірний розрахунок стержня або деталі на міцність?
9.5 За якою формулою визначається величина допустимої напруги для пластичного і для крихкого матеріалів?
9.6 Для чого призначенні епюри поздовжніх сил і нормальних напруг по довжині стержня, яких правил треба дотримуватись при їх побудові?
9.7 Напишіть формулу – умову міцності при розтягу і стиску, надайте її пояснення.
Самостійна робота № 6
1 Тема
Проектний розрахунок веденого валу редуктора із умови міцності при крученні
2 Мета
Навчитись виконувати проектний розрахунок однієї із деталей редуктора; усвідомити сутність міжпредметних зав’язків теоретичної механіки, опору матеріалів і деталей машин.
3 Інформаційне забезпечення
Теоретичні відомості [1…9]
4 Методичні вказівки
Загальні відомості
Проектний розрахунок валів редукторів виконується в процесі виконання курсового проекту або курсової роботи з блоку 3 «Деталі машин». Такий розрахунок доречно виконати кожному студенту технічної спеціальності, тому що така самостійна робота допомагає усвідомити сутність і зв'язок набутих знань з теоретичної механіки, опору матеріалів і деталей машин. Ведений вал будь-якого закритого редуктора – циліндричного, конічного чи черв’ячного має типові ділянки, кожна із яких має певне призначення в конструкції редуктора, наприклад:
- вихідний кінець валу призначений для з’єднання редуктора з іншими механізмами або із робочими машинами в приводі;
- шип або цапфа призначенні для закріплення на цих ділянках опор валу, наприклад стандартних підшипників кочення з метою забезпечення обертального руху валу і зубчастого колеса, закріпленого на ньому;
- головка валу призначена для закріплення веденого колеса на валу з допомогою призматичної шпонки;
- упорний буртик призначений для запобігання зміщення ведених колес вздовж валу під час їх зачеплення з ведучими шестірнями або черв’ячним гвинтом; по величині діаметра буртика підбирають потім заготовку для виготовлення веденого валу згідно отриманим при проектних розрахунках розмірам.
Проектний розрахунок валу із умови міцності при крученні виконується як попередній, тобто спрощений – це докладно обґрунтовується в предметі «Деталі машин» і на відповідному занятті з технічної механіки. На практичному занятті, яке передує самостійній роботі № 4 достатньо коротко обґрунтувати призначення подібних розрахунків і розв’язати типову задачу.
Самостійна робота № 6 виконується в такій послідовності:
- у відповідності із заданою в умові кінематичною схемою привода уточнити порядковий номер веденого валу редуктора (другий чи третій);
- визначити величину обертаючого моменту на цьому валу, прирівняти його до крутного моменту МК;
- визначити необхідний діаметр вихідного кінця валу із умови міцності при крученні за формулою: 16М k
d вих 3,
k
де [τк] – задана допустима напруга матеріалу валу при крученні; її величину рекомендується призначати в межах 20…70 МПа залежно від марки сталі і прийнятого коефіцієнту запасу міцності;
- закруглити отриману розрахункову величину до найближчого
стандартного значення, кратного «2» або «5»;
- діаметри інших ділянок валу визначаються конструктивно – на основі рекомендацій [7] та [8]: діаметр шипа валу dш = dвих + (3…10мм) і обов’язково повинен бути кратний «5»; діаметр головки валу dгол = dш + 5мм; діаметр упорного буртика dб = dгол + 10мм.
Примітка: діаметри шипів та цапф валів повинні бути кратними «5», тому що промисловість випускає стандартні підшипники кочення з внутрішнім діаметром кратним «5».
Після розрахунків можна рекомендувати студентам виконати ескіз спроектованого валу з метою перевірки правильності рішення, для наочності та закріплення міжпредметних зв’язків технічної механіки та інженерної графіки. Довжини ділянок призначити від 30 до 100 мм залежно від призначення даної ділянки валу.
Для студентів спеціальності 5.092207 виконання самостійної роботи № 4 сприятиме підготовці до виконання курсової роботи з технічної механіки. Перед вирішенням задачі до СР № 6 слід уважно розглянути складальне креслення вузла веденого валу циліндричного закритого редуктора із 14 деталей, спробувати вказати їх назву та призначення (рис. 6.1)
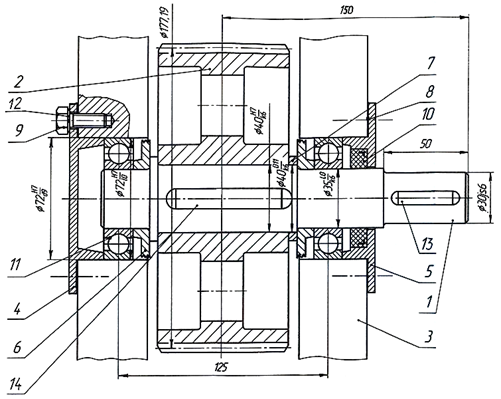
Рисунок 6.1 Складальне креслення вузла веденого валу редуктора
5 Приклад розв’язку задачі до СР № 6
5.1 Завдання
Виконати проектний розрахунок веденого валу закритого конічного редуктора (рис. 6.2), який входить до складу двоступінчастого приводу конвеєра. Матеріал валу – сталь 45, допустиму напругу прийняти [τк] = 50 МПа. Виконати ескіз спроектованого ступінчастого валу редуктора згідно отриманим розмірам.
5.2 Умова задачі
Кінематична схема привода (рис. 6.2) і вихідні дані
Рдв = 5 кВт; nдв = 720 об/хв; d1 = 100 мм; d2 = 300 мм; иред = 3,15; ηред = 0,95; ηпас = 0,98; [τк] = 50 МПа.
Рисунок 6.2 Кінематична схема привода до задачі
5.3 Опис схеми: привод складається із електродвигуна, клинопасової передачі – першого ступіня привода, закритого конічного редуктора – другого ступіня привода, муфти, робочої машини – конвеєра. Ведений вал редуктора є третім валом привода.
5.4 Кінематичні параметри привода:
Передаточні числа
и1ст = d2/d1 и1ст = 300/100 = 3;
и2ст = и ред = 3,15 (за умовою); 5.5 Силові параметри привода:
Обертаючі моменти на валах привода, Н*м
Т1в = М1в = Мдв = 9,55;
Т1в = М1в = 9,55*5*10³/720 = 66,3;
Т2в = М2в = М1в = М1в* и 1*η1
Т2в = М2в = 66,3*3*0,95 = 189;
Т3в = М3в = М2в = М2в* и 2*η2
Т3в = М3в = 189*3,15*0,98 = 583.
5.6 Розміри діаметрів ділянок веденого валу редуктора
5.6.1 Діаметр вихідного кінця веденого валу закритого конічного редуктора dвих, мм:
16Т3в
dвих 3,
k
де Тзв дорівнює крутному моменту МК при визначенні діаметра валу із умови міцності при крученні: МК = 583Нм;
16 583 10 3
d 3 39. вих 50
Призначається стандартне значення dвих = 40 мм. 5.6.2 Діаметр шипів валу, мм dш = dвих + 5 dш = 40 + 5 = 45;
5.6.3 Діаметр головки валу, мм dг = dг + 5 dг = 45 + 5 = 50;
5.6.4 Діаметр упорного буртика
dб = dб + 10 dб = 50 +10 = 60.
6 Зображення ескізу веденого валу редуктора згідно отриманим розмірам
(рис. 6.3).
Довжини ділянок валу , мм призначаються конструктивно:
- довжина вихідного кінця валу l = 1,5*dвих = 1,5*40 = 60;
- довжина шипів валу l = 35;
- довжина головки валу l = 100;
- товщина упорного буртика l = 5.
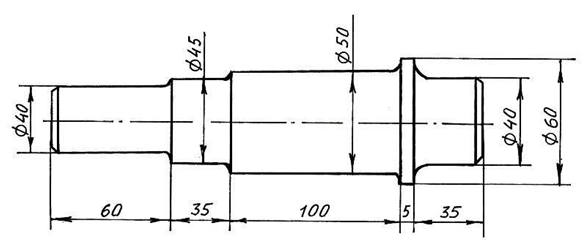
Рисунок 6.3 – Ескіз спроектованого веденого валу закритого конічного редуктора у відповідності з умовою задачі до СР № 6
Таблиця 6.1 Числові значення параметрів згідно рис. 6.4
|
Номер варіанту задачі |
Потужність двигуна, Рдв, кВт |
Частота обертання валу двигуна пдв, об/хв |
Передаточне число редуктора иред |
Коефіцієнти корисної дії |
Допусти ма напруга сталі при крученні [к], МПа |
|
|
ред |
пас(ланц) |
|||||
|
1 |
5 |
700 |
4 |
0,98 |
0,95 |
35 |
|
2 |
7 |
1400 |
16 |
0,90 |
0,95 |
45 |
|
3 |
3 |
950 |
3,55 |
0,97 |
0,92 |
50 |
|
4 |
12 |
1450 |
12 |
0,88 |
0,92 |
40 |
|
5 |
6 |
920 |
2 |
0,96 |
0,92 |
60 |
|
6 |
4 |
730 |
2,8 |
0,98 |
0,92 |
30 |
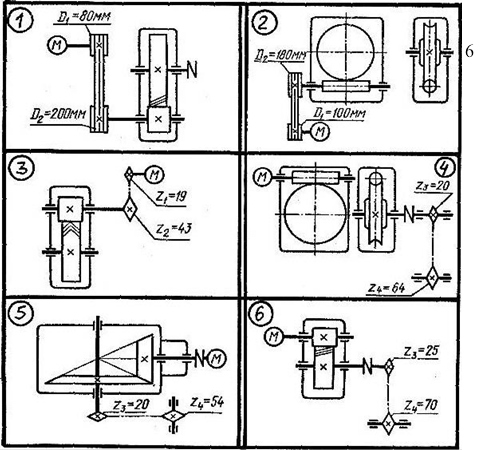
Рисунок 6.4 – Приклади варіантів завдань.
7 Контрольні питання
7.1 Чому один із валів редуктора називається веденим?
7.2 Назвіть основні конструктивні елементи веденого валу закритого редуктора та поясніть їх призначення.
7.3 Напишіть формулу «умова міцності при крученні» і надайте пояснення величинам, що входять до неї.
7.4 Напишіть формулу, за якою визначається діаметр вихідного кінця веденого валу редуктора і надайте їй пояснення.
7.5 Чому діаметр шипа валу повинен обов’язково бути кратним «5»?
Список літератури
1 Аркуша, А.И. Техническая механика. Теоретическая механика и сопротивление материалов: Учебник для средних спец. учеб. заведений/ А.И.Аркуша. – 5-е изд., стер. - М.: Высшая школа, 2003. – 352 с.
2 Аркуша А.И. Техническая механика. Теоретическая механика и сопротивление материалов: учебник. – М.: Либроком, 2015. – 354 с.
3 Вереина, Л. И. Краснов, М. Н. Техническая механика: учебник для студентов образовательных учреждений СПО.- М: Академия , 2010.
4 Вереина, Л. И. Сборник задач по технической механике: учебное пособие для студентов образовательных учреждений СПО.- М: Академия , 2010.
5 Ивченко, В.А.Техническая механика: Учебно-методический комплекс. – М.:ИНФРА-М, 2004.
6 Ивченко, В.А. Техническая механика: Учебное пособие. – М.:ИНФРА- М, 2003.
7 Ердеді О.О. та ін. Технічна механіка. – К.: Вища школа, 1983 – 368 с.
8 Олофинская, В.П.Техническая механика: Курс лекций с вариантами практических и тестовых заданий: Учебное пособие. – М.: ФОРУМ: ИНФРА-М, 2012. – 348 с.
9 Мовнин М.С. и др. Основы технической механики. – Л.:
Машиностроение, 1982. – 288 с.
10 Аркуша А.И. Техническая механика. Теоретическая механика и сопротивление материалов: учебник. – М.: Либроком, 2015. – 354 с.
11 Эрдеди А.А., Эрдеди Н.А. Техническая механика: учебник. – М.: Academia, 2014. – 528 с.
Додаток А
42
про публікацію авторської розробки
Додати розробку