Технологія Ірини Стеценко

Технологія Ірини Стеценко «Логіки світу»

Біографія про розробника Ірина Стеценко закінчила Київський політехнічний інститут, за фахом — інженер-математик. Але ще раніше, ніж стала інженером, стала вчителем: уже на четвертому курсі працювала вчителем інформатики в старших класах спеціалізованої школи, потім — у середніх і молодших, а після закінчення вишу прийшла в дитячий садок. Має досвід роботи з дітьми від 3-х до 17-ти років. Так і народилася розвивальна технологія «Логіки світу» для дітей від 4 до 12 років.

Усі знання математика й інженера передає в статтях, книгах і на семінарах вихователям, вчителям, студентам: не завжди в наших програмах є глибина й широта знань, необхідна зараз уже в дитячому садку. 

Працює на даний момент науковим співробітником у Міжнародному науково-навчальному центрі інформаційних технологій і систем Національної академії наук України й Міністерства освіти і науки України. Автор більше 200 статей і понад 20 книг (керівник Катерина Крутій).

Основна наукова тема — застосування інформаційних технологій у дошкільній та початковій освіті. Приділено великій увазі розвитку мислення дітей: адже вміння нестандартно вільно мислити, виробляти нові ідеї, доводити правильність своїх висновків, життєздатність своїх теорій необхідні фахівцеві будь-якої галузі — від артиста до інженера. Звучить дуже строго, не по-дитячому серйозно? Але зараз час такий: щоб іти вперед треба багато чого вміти й знати, учитися переборювати труднощі, бачити мету й завзято йти до неї, бути оптимістом, уміти радіти навіть маленьким удачам... А основи цього народжуються в кожної людини вже в дитячому садку.

Сьогодні система дошкільного навчання має, на погляд Ірини Стеценко , давати дітям не лише знання, а й сприяти розвитку творчого мислення й інтелектуальних здібностей. Одним з основних завдань педагога має бути завдання не просто накопичення знань дітей, а завдання навчити їх міркувати, грамотно обгрунтовувати свою точку зору, самостійно приймати рішення, не боятися задач з багатьма варіантами розв’язку. Цій меті сприяє впровадження у навчання розвивальних курсів, які побудовані на основі нових інформаційних технологій. «Логіки світу» є одним з прикладів такого курсу .

Чому технологія називається саме так? Для кожного типу завдань визначаються об’єкти вивчення (об’єкти навколишнього світу), операції над ними і правила їх використання, тобто для кожного типу завдань задається логіка. Об’єкти вивчення і операції над ними вибираються зрозумілі і цікаві для дитини, тому малюки швидко і невимушено орієнтуються. Вони навіть можуть придумувати свої операції над об’єктами логіки.

Починати розвивати мислення дітей потрібно вже під час навчання в дитячому садку: потім (в старших класах школи). Буде важко надолужити те, що втрачено, зробити мислення дітей нестандартним, навчити їх міркувати самостійно. Тому за технологією «Логіки світу» навчаються діти від 4 до 12 років. Технологія «Логіки світу» призначена для всіх дітей, а не тільки для математично обдарованих. (До речі, в ранньому віці в більшості випадків ще неможливо визначити наскільки потрібна буде математика в подальшому житті дитини, зате точно відомо, що кожній дитині потрібно вміти самостійно міркувати, яку б спеціальність вона не обрала.)

Заняття за технологією «Логіки світу» проводяться у формі інтелектуальної гри. Діти в легкій для сприйняття, цікавій формі розв’язують оригінальні математичні завдання, завдання з геометрії, теорії множин, математичної логіки, конструювання, комбінаторики, завдання, що сприяють естетичному вихованню та розвитку загальної культури дітей.

Для вирішення завдань від дітей не вимагається якихось особливих математичних знань. Більш ніж достатньо тих знань з математики, якими діти оволодівають в звичайному дитячому садку і в звичайній школі: вони повинні знати основні типи геометричних фігур (квадрат, прямокутник, круг, трикутник, чотирикутник, багатокутник) і вміти рахувати.

На заняттях технології «Логіки світу» малята із задоволенням розв’язують завдання пошуку закономірностей вибору й розташування геометричних фігур, складних об’єктів та їх композицій; завдання на конструювання багатокутників та силуетів за розділеними і нерозділеними зразками; завдання-ігри з використанням правил; завдання про випадкові та вірогідні події; завдання на вкладеність геометричних фігур тощо.

Діти закріплюють свої уявлення про геометричні фігури, вчаться розділяти складні фігури на більш прості, порівнювати предмети за різними ознаками, домагатися поставленої мети, використовуючи лише заданий (чітко обмежений) набір засобів - елементів для конструювання та правил їх використання.

При рішенні завдань, необхідно звертати увагу не тільки на правильність розв’язку кожного завдання (дитина може знайти свій власний варіант відповіді), а й на обґрунтування рішення. Дитина може, на погляд дорослого, розв’язати завдання неправильно, але, особливо в цьому випадку, потрібно звернути увагу на обґрунтування відповіді. Дитина повинна, насамперед, навчитись доводити, що її рішення також можна вважати правильним. Це той випадок, коли пояснення і процес розв’язку завдання можуть бути важливішими ніж сам результат розв’язку.

Багато завдань мають кілька варіантів розв’язку. Знайдіть разом з дитиною кілька варіантів рішення такого завдання і проаналізуйте їх. Які розв’язки схожі один на одного, а які відрізняються один від одного? Чим відрізняються розв’язки? Яке завдання має лише одне рішення? Спробуйте пояснити, чому це завдання має тільки одне рішення.Із завдань кожного типу будуються ланцюжки за принципом «від простого до складного» так, що найпростіші завдання діти розв’язують без великих труднощей, поступово завдання ускладнюються і, дитина в більшості випадків навіть не помічає переходу від простих завдань до складних.

Ланцюжки завдань, гарні тим, що проблема складності, неможливості розв’язати завдання не стоїть перед дитиною. Завдання не лякають складністю, а навпаки, приваблюють дітей результатом рішення (яскравий малюнок, прикраса для ялинки тощо). У дітей не губиться цікавість до навчання та до предмету, що вивчається. Вони фантазують, вигадують свої цікаві завдання, навчаються за допомогою гри. Давайте роздивимось завдання з такого ланцюжка, у яких потрібно знайти закономірності в розташуванні геометричних фігур і різноманітних складних об’єктів в рядах. У найпростіших завданнях діти шукають закономірності розташування геометричних фігур у ланцюжках. Деякі з цих завдань пропонуються навіть дітям 4 років.

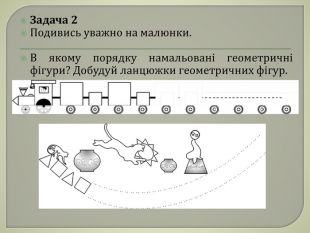
Задача 1 Уважно роздивись цей малюнок. Розкажи, в якому порядку розташовані квадрати в ланцюжку. Обведи олівцем наступний квадратик в ланцюжку. Намалюй сам останній квадратик цього ланцюжка. Уважно роздивившись малюнок, діти часто відповідають: «Хтось построїв квадрати за зростом». Не наполягайте на точності відповіді відразу ж (в перших завданнях). Діти висловлюють свою думку так, як розуміють. Вони намагаються порівняти порядок розташування фігур з тим, що вони бачать у повсякденному житті. Їх порівняння бувають дуже влучними і, найголовніше, зрозумілі для них. Але зроблено лише перший крок до відповіді.

Задайте дітям додаткові запитання, і їх відповідь стане більш точною. Розкажи, який квадратик стоїть першим в ланцюжку? Чим він відрізняється від останнього? Чим перший квадрат відрізняється від наступного квадрата в ланцюжку? Розкажи, як розташовані квадрати в ланцюжку? «Ланцюжок починається з найменшого квадрата, потім намальовано більший квадрат, потім — ще більший… Останній квадрат ланцюжка — найбільший». Після такої розмови дітям вже неважко самостійно намалювати останній квадрат ланцюжка. Потім можна розв’язувати завдання на пошук складніших закономірностей.

Задача 2 Подивись уважно на малюнки. В якому порядку намальовані геометричні фігури? Добудуй ланцюжки геометричних фігур.

При рішенні таких задач дитина навчається знаходити послідовності розташованих поряд геометричних фігур, що повторяються. Як тільки така послідовність знайдена, дитина досить швидко будує продовження ланцюжка геометричних фігур. Якщо у дитини виникають труднощі при пошуку таких закономірностей, запропонуйте їй розказати, які геометричні фігури входять в даний ланцюжок. Нехай дитина поміркує над порядком розташування геометричних фігур в заданому ланцюжку.

Геометричні фігури в ланцюжку розташовані в якомусь визначеному порядку чи ні? Які геометричні фігури повторяються в ланцюжку? Чи є в ланцюжку кілька розташованих поруч геометричних фігур, які потім повторяються?Тепер вже нескладно виділити геометричні фігури в ланцюжку, що повторяються, і побудувати продовження даного ланцюжка відповідно до знайденої закономірності. Навіть якщо дитина легко знаходить закономірності розташування геометричних фігур, обов’язково запропонуйте їй обґрунтувати свою відповідь. Чому побудовано саме таке продовження ланцюжка геометричних фігур?

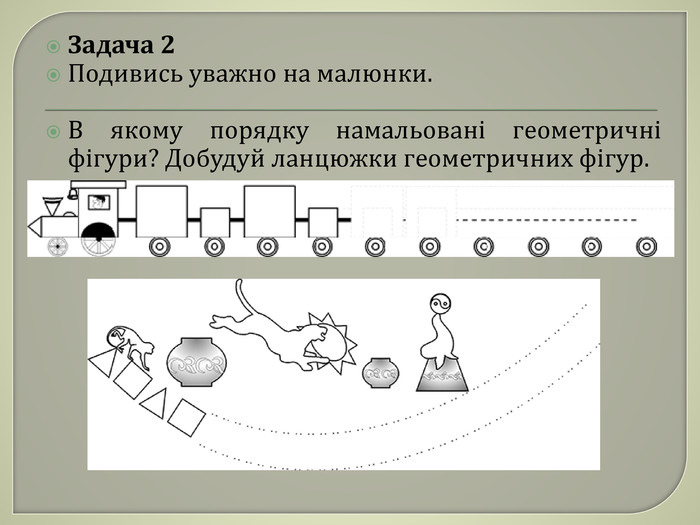
У технології пропонуються задачі на пошук закономірностей в розташуванні більш складних об’єктів (хатинок, ялинок, квітів тощо). В таких завданнях діти вставляють в ряд пропущені предмети або продовжують ряд предметів відповідно до знайденої закономірності. Під час рішення особливо важливо навчити дітей обґрунтовувати його, оскільки досить часто діти знаходять багато варіантів. Педагог завжди повинен пам’ятати, що діти міркують по-своєму, і тому знаходять навіть такі варіанти рішень, про які доросла людина і подумати не могла б. Розгляньте  з дітьми різні варіанти рішення завдання, і обов’язково вислухайте пояснення дітей до рішень. За допомогою саме таких завдань діти навчаються розглядати проблему «під різними кутами зору», порівнювати різні варіанти рішень, сприймати іншу точку зору, слухати пояснення іншої людини.

Задача 3 Подивись уважно на малюнок. Як ти гадаєш, що я пропустив? Домалюй там, де стоїть знак запитання. Поясни своє рішення.

У задачі намальована ціла вулиця хатинок. Одна хатинка пропущена. Деякі хатинки відрізняються одна від одної вікнами, дахами, у одних хатинок з труби на даху йде дим, а у інших — ні. Який вигляд має пропущена хатинка? У складі кожної хатинки є однаковий квадрат. З нього ми й почнемо малювати пропущену хатинку. Далі визначимо, який у пропущеної хатинки буде дах. Дахи у хатинок повторюються через один, тому у пропущеної хатинки має бути дах, схожий на трапецію. Вікна у хатинок теж повторюються через одне, тому у пропущеної хатинки вікно буде круглим. Димохід є у кожної хатинки, тому ми намалюємо його і в пропущеної. Тепер поміркуємо, чи буде з димоходу йти дим. Якщо уважно подивитись на малюнок ми помітимо, що серед перших трьох хатинок диму немає тільки в середній; у наступній і останній хатинках дим є. Тому і у пропущеній хатинці дим з димоходу не йтиме. От і намалювали ми пропущену хатинку на вулиці.

При розв’язуванні таких задач запропонуйте дитині уважно роздивитися, що зображено на малюнку. Чи є щось спільне в усіх зображених предметів? Чим предмети на малюнку відрізняються один від одного? Відповідно до якої закономірності змінюється кожна частинка намальованих предметів?

Задача 7 Подивись уважно на малюнок. В якому порядку намальовані геометричні фігури? Заверши ланцюжки геометричних фігур.

У задачах на пошук закономірностей, необхідно враховувати одразу кілька властивостей геометричних фігур або предметів: тип, величину, колір тощо. Під час дослідження висувається набагато менше гіпотез, ніж у попередніх завданнях. Іноді легше знаходити закономірності у два (або більше) етапів: спочатку — зосередити увагу на формі й величині геометричних фігур, потім — розфарбувати їх. З часом діти навчаться зосереджувати увагу одразу на всіх властивостях об’єктів у ланцюжках. Роздивившись малюнок, вони можуть лише сказати, що для подовження цього ланцюжка використовуватимуться тільки маленькі квадрати, великі трикутники й великі прямокутники. Іноді вони одразу називають і кольори геометричних фігур. Тепер можна починати висувати гіпотези. Для цього дітям необхідно знайти в ланцюжку групу геометричних фігур, що повторюється. Можливо, наступною фігурою в ланцюжку буде великий трикутник?

Для нашого завдання пояснення закономірності можуть бути такими:1. Ланцюжок починається з маленького квадратика, другою фігурою в ньому квадрат і так далі. Кольори фігур у ланцюжку змінюються так: червоний, жовтий, зелений і так далі.2. Перша фігура ланцюжка — маленький червоний квадрат, за ним завжди стоїть великий жовтий трикутник, потім — великий зелений прямокутник. За великим зеленим прямокутником — маленький червоний квадрат і т. д.3. Фігури в ланцюжку розташовані трійками — маленький червоний квадрат, великий жовтий трикутник, великий зелений прямокутник, — які стоять одна за одною.

Задача 8 Уважно подивися на малюнок. Як ти вважаєш, що я недомалював? Домалюй там, де стоїть знак запитання. Поясни свої дії.

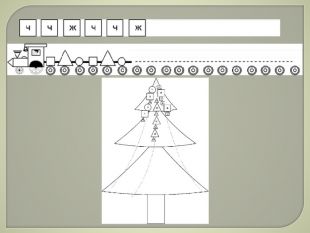
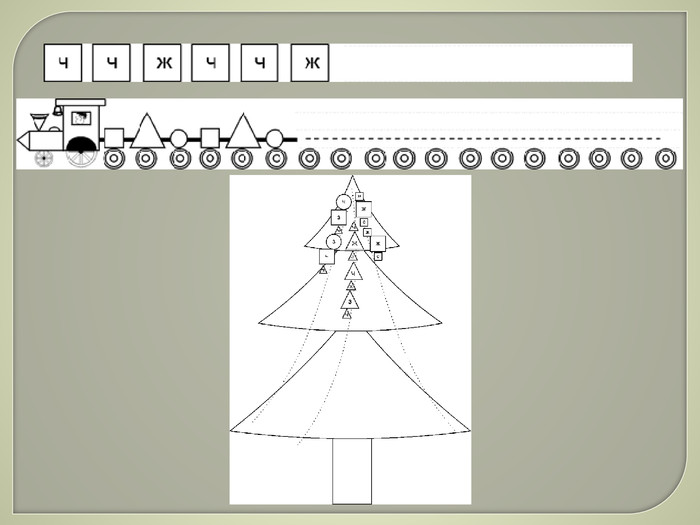
Початок етапа постановки проблеми майже нічим не відрізняється від попередньої задачі. Але яким буде результат дослідження? Скільки ялинок ми намалюємо? Чи закінчиться ланцюжок? В залежності від відповідей на ці запитання ланцюжок буде скінченим або нескінченим, ялинки у ланцюжку будуть повторюватися або будуть різними.  Тому на етапі постановки проблеми вони намагаються передбачити яким буде ланцюжок в результаті розв’язку. Не потрібно одразу вимагати від них правильної відповіді, достатньо вже й того, що діти міркували над нею: зрозуміли, що в результаті ланцюжок може бути скінченим або нескінченим; намагалися заздалегідь передбачити результат. Поступово малюки навчатимуться точно передбачати вигляд результату рішення. В усіх задачах на пошук закономірності діти лише у загальному вигляді передбачають вигляд майбутнього результату (немає сенсу висування гіпотез, якщо вже на першому етапі дослідження повністю намальовано ланцюжок): з яких геометричних фігур складатиметься продовження ланцюжка, скінченим або нескінченим він буде.

Тепер діти висувають гіпотези, одразу обгрунтовують їх і викладають продовження ланцюжка. Варіантів рішення:

Комбінаторика в дизайні Розв’язувати такі задачі нам допомагає комбінаторика — розділ математики, який вивчає кількість комбінацій, що задовольняють певним умовам. Комбінації можна складати з будь-яких елементів із заданої множини. Але комбінаторика вказує лише напрям, яким потрібно йти. А як саме йти — визначає людина.

Тож щоб розв’язувати такі задачі необхідно бути вигадливим і уважним, знайти спосіб порівняння знайдених варіантів на повноту і оптимальність. Знайти всі можливі варіанти нам можуть допомогти системи числення. Закодуємо кольори (або напрями) цифрами, тоді всі числа з певною кількістю розрядів і будуть різними варіантами розв’язку комбінаторних задач. Розглянемо задачі про розфарбування прапорців у смужечку. Скільки різних прапорців можна скласти з двох смужечок різного кольору? Звичайно, дуже проста задача, її без помилок розв’яже навіть дошкільнятко. А тепер додамо смужечок і кольорів: задача суттєво ускладнюється. Дослідимо розв’язування цієї задачі за допомогою двійкової системи числення (адже у нас всього два кольори, тож двох цифр вистачить для їх кодування). Одразу зауважу, що саме двійкова система числення використовуватиметься для представлення інформації у комп’ютерах. Тож такі задачі допоможуть надати знань і про системи числення, показати оригінальний спосіб їх використання.

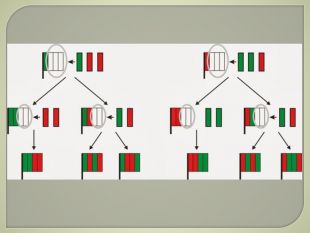
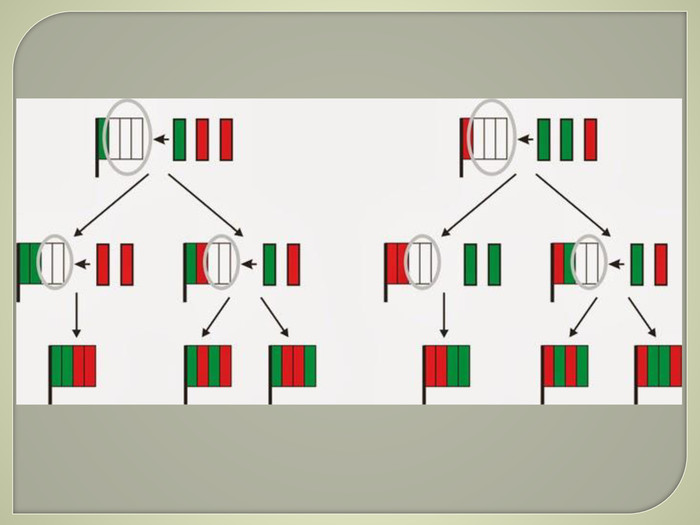
Задача 12 У мене є чотири однакові за величиною стрічки: дві — червоного кольору і дві стрічки зеленого кольору. Допоможи мені скласти з них до свята якомога більше різних прапорців. Кожен прапорець складається з чотирьох стрічок. Розфарбуй ці прапорці. Закресли “зайві” прапорці, якщо я намалював прапорців більше, ніж їх можна скласти.

Це завдання з комбінаторики. Спочатку діти мають розібратися в умові задачі, уявити, з яких саме стрічок складається кожен прапорець. Кожен прапорець обов’язково складається з чотирьох стрічок (двох зелених і двох червоних), які розташовані вертикально одна біля одної. Необхідно знайти якомога більше різних варіантів розташування стрічок у прапорцях. Полічимо скільки різних прапорців можна побудувати.

Постановка проблеми цілком зрозуміла. Результатом дослідження буде малюнок з прапорцями, розфарбованими по-різному, кожен прапорець складатиметься з двох червоних і двох зелених стрічок. Скільки таких прапорців ми намалюємо можна полічити під час вирішення задачі.

Сходинки маленького дослідника: теорія графів. Обведи малюнок, не відриваючи олівця від паперу і не проводячи двічі по одній і тій самій лінії. Покажи, де ти починав обводити фігуру. Стрілочками вкажи, як рухався твій олівець.

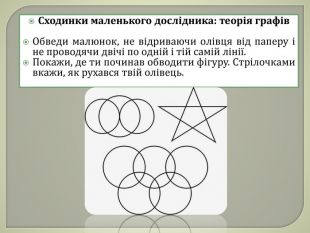
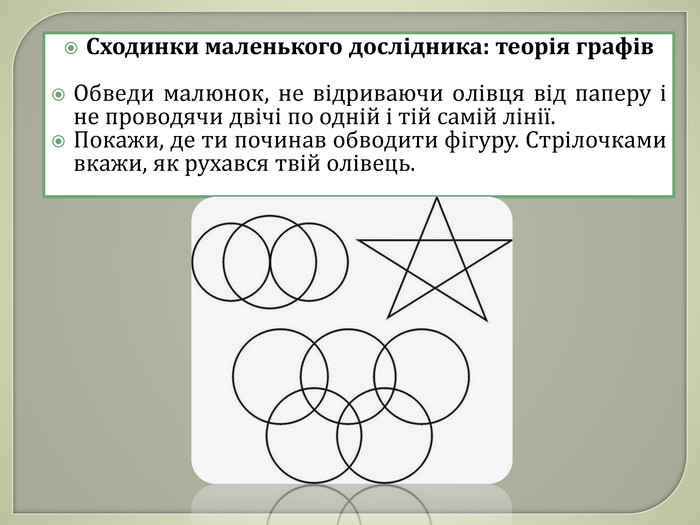
Проміжні результати етапів можуть бути такими:знайти ознаки фігур, які неможна обвести, не відриваючи олівця од паперу;знайти ознаки фігур, які можна обвести, не відриваючи олівця од паперу і не проводячи двічі по одній і тій самій лінії;знайти ознаки фігур, які можна обвести, не відриваючи олівця од паперу і не проводячи двічі по одній і тій самій лінії, починаючи і закінчуючи обведення в одній і тій самій вершині.

Дякую за увагу!Виконала: Григорчук Тетяна. Студентка: 1 МАП