Текст олімпіадні завдання
1.У виразі 6*5*4*3*2*1
------------------- = 17 поставити замість зірочок
8*7
знаки «+» або «-« так, щоб отримана рівність була правильною.
6+5+4+3-2+1 = 17
8-7
2.Знайти найменше число, яке записується за допомогою лише одиниць та ділиться на число, складене із ста трійок.
(Відповідь :число, яке записане за допомогою 300 одиниць)
3.Знайти всі такі сто цифрові числа а, які задовольняють рівність: а:= «сума всіх цифр числа а»+ «сума всіх попарних добутків цих цифр» + «сума всіх добутків по три цифри» + …+ «добуток всіх цифр».

- У виразі 6*5*4*3*2*1
------------------- = 17 поставити замість зірочок
8*7
знаки «+» або «-« так, щоб отримана рівність була правильною.
6+5+4+3-2+1 = 17
8-7
- Знайти найменше число, яке записується за допомогою лише одиниць та ділиться на число, складене із ста трійок.
(Відповідь :число, яке записане за допомогою 300 одиниць)
- Знайти всі такі сто цифрові числа а, які задовольняють рівність: а:= «сума всіх цифр числа а»+ «сума всіх попарних добутків цих цифр» + «сума всіх добутків по три цифри» + …+ «добуток всіх цифр».
(Вказівка: умову задачі запишіть у вигляді рівняння
в1*10 + в2*10+ в3*10+…..+в99*10+в100= (в1+1)(В2+1)…(В100+1) -1 ОЦІНІТЬ ЙОГО ПРАВУ ЧАСТИНУ. Відповідь: числа виду в199…99, де в1- довільна цифра, відмінна від 0
- У трикутнику АВС висота АН дорівнює медіані ВМ .Знайти кут МВС.
Відповідь: 30°
- У трикутнику АВС сторона АС вдвічі більша за сторону ВС, а ∟С=2∟А. Знайти кути трикутника.
Відповідь:∟А=30, ∟С=60, ∟В=90
Ігрові задачі
- Маємо три купи каменів: у першій -10, у другій -15, у третій – 20. За хід дозволяється розділити будь-яку купу на дві менші; програє той, хто не може зробити хід.
Розв’язання.
Наприкінці гри коли не можна зробити хід , маємо 45 куп по одному каменю. За будь-який хід куп збільшується на одиницю, тому вся гра має тривати точно 45-3=42 ходи.
Отже другий гравець завжди виграє.
- Двоє гравців по черзі виймають із двох ящиків кулі. За один хід кожен гравець може брати з будь-якого (тільки одного) ящика довільну кількість куль. Виграє той, хто бере останнім. Як має грати той гравець, що починає, щоб виграти, якщо в першому ящику 73 кулі, а в другому – 118 куль?
Розв’язання.
Якщо перший гравець спочатку візьме 45 куль з другого ящика стане куль порівну. Після цього перший гравець на кожен хід суперника має симетричну відповідь, тобто, якщо другий бере 6 куль з якогось ящика, то перший має брати 6 куль з іншого ящика.
- Двоє по черзі ставлять слонів на клітинки шахової дошки так, що слони не б’ють один одного. (Колір слонів значення не має). Програє той, хто не може зробити хід.
Розв’язання. Шахова дошка симетрична відносно свого центра, тому, на перший погляд, другий гравець на кожен хід першого має симетричний хід. Однак це не так , бо, якщо перший гравець ставить слона на одну з клітинок головної діагоналі, то другий гравець симетричного ходу не має.
Щоб розв’язати за допомогою симетричної стратегії, необхідно знайти симетрію, при якій попередній хід суперника не перешкоджає дотриманню обраної стратегії. Такою є симетрія відносно прямої, що розділяє четверту і п’яту горизонталі. Симетричні відносно неї поля мають різний колір, і тому слони, поставлені на такі поля, не б’ють один одного.
Отже, другий гравець виграє, якщо на кожен хід першого гравця відповідає ходом, симетричним відносно вказаної прямої.
- У коробці знаходяться 60 сірників. За один хід можна взяти будь-яку кількість від 1 до 5 сірників. Програє той , хто не може зробити хід. Хто з гравців може забезпечити собі виграш?
Розв’язання.
Проаналізуємо кінцівку гри . Якщо кількість сірників менша за 5, то той гравець, чия черга ходити, закінчує гру. Якщо кількість сірників більша за 6, то гра закінчується через два або більше ходи. Якщо ж кількість сірників дорівнює 6, то гравець, чий хід передував цій позиції, точно наступним своїм ходом закінчує гру. ( для цього він на хід суперника в к сірників бере 6-к сірників). Тобто така позиція є виграшною для цього гравця. Очевидно, що позиції 12, 18,24 (і т.д.) сірників для нього також є виграшним, бо таким самим способом він від позиції «24 сірники» переходить до позиції «18 сірників», від «18» до !12!.
Отже початкова позиція виграшна для другого гравця, а його виграшною стратегією є доповнення ним ходів першого гравця до 6 сірників.
- Два хлопчики пишуть по черзі к-значне число: першу цифру пише перший, другу – другий, третю – перший і т.д. Чи може хлопчик добитися того, щоб отримане число ділилося на 9, якщо перший старається йому завадити? Розглянути випадки а) к=10; б) к=13.
Відповідь: виграшна стратегія – доповнення до числа 9, щоб сума ділилася на 9
А) може виграти другий
Б) не може виграти другий бо останнім пише перший хлопець.
- Двоє по черзі кладуть однакові монети на круглий стіл, причому так, щоб іони не накладалися одна на одну. Програє той, хто не може зробити хід.
Вказівка. Перший хід такий, щоб центр стола і центр монети збігалися, потім центральносиметрична стратегія. Відповідь: виграє перший гравець.
- На столі лежало 1978 сірників. Два хлопчики по черзі можуть брати 1 чи 2 сірники. Який хлопчик виграє і як він має грати для цього?
Відповідь: перший гравець. Перший хід – один сірник, виграна стратегія – доповнення до 3.
- На колі розставлено 20 точок. За хід дозволяється сполучити будь-які дві з них відрізком, що не перетинає відрізків які проведені раніше. Програє той, хто не може зробити хід.
Відповідь: перший гравець, Перший хід провести хорду , по обидва боки від якої розміщено по 9 точок. Виграшна стратегія – симетричні ходи.
- Двоє гравців по черзі ставлять коней на клітинки шахової дошки так, що коні не б’ють один одного. Програє той, хто не може зробити хід.
Відповідь – другий гравець. Виграшна стратегія –центральна або осьова стратегія.
- Ромашка має: а) 12 пелюсток;б) 11 пелюсток.
За хід дозволяється відірвати або одну, або дві пелюстки, що ростуть поруч. Програє той, хто не може зробити хід.
Відповідь : Другий гравець. Незалежно від першого ходу суперника може залишити після свого ходу два однакові за довжиною ланцюжки пелюсток, після чого буде застосовувати симетричну стратегію.
- Гра починається з 1000. За хід дозволяється відняти від наявного будь-яке, яке не перевищує його, натуральне число, що є степенем двійки (1=2°). Виграє той, хто одержить нуль.
Відповідь: перший гравець. Виграшні позиції – числа , які діляться на 3.
- Гра починається з числа 1. за один хід дозволяється помножити наявне число на будь-яке натуральне число від 2 до 9. Виграє той, хто перший одержить число більше за 1000.
Виграшні позиції – числа від 56 до 111 та числа від 4 до 6. Відповідь :перший гравець.
- Двоє по черзі ставлять хрестики і нулики в клітинки дошки 9х9 Перший гравець ставить хрестик, другий – нулик. Наприкінці гри треба підрахувати, скільки є рядочків і стовпчиків, у яких хрестиків більше, ніж нуликів – це є очки, набрані першим гравцем. Кількість рядків і стовпчиків, де нуликів більше – очки другого гравця. Перемагає той , у кого більше очок.
Відповідь : перший гравець. Перший хід він робить у центральну клітинку, потім робить симетричні ходи відповіді.
- Є дві купи сірників: а) 101 сірник і 201 сірник;
Б) 100 і 201 сірник. За хід дозволяється зменшити в одній з купок на число, що є дільником кількості сірників в іншій купці. Виграє той , після ходу якого сірників не залишається.
Вказівка : виграшні ті позиції, при яких у кожній купі непарна кількість сірників. Відповідь: а) другий ,б) перший.
- Гра починається з числа 2 .За хід дозволяється додати до наявного числа будь-яке натуральне число, менше за нього. Виграє той , хто одержить 1000.
Відповідь: перший. Вказівка: виграшні позицій: 3,7,15,31,62,125, 250, 500.
Розміщення фігур на площині
- До кожної сторони квадрата прикладено такий самий квадрат. Потрібно перетворити утворену «хрестоподібну» фігуру в квадрат за допомогою чотирьох прямолінійних розрізів і переміщень утворених частин.
Відповідь.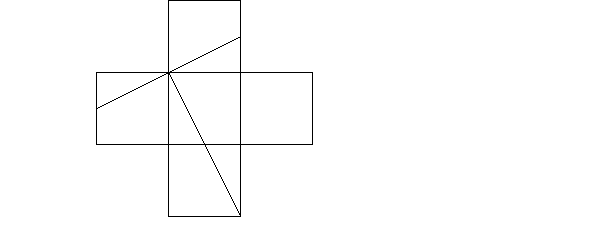


про публікацію авторської розробки
Додати розробку
