Тема: Дослідження функцій на монотонність

Тема: Дослідження функцій на монотонність

Мета: Ознайомити студентів з поняттям зростання (спадання) функції, розуміти проміжки монотонності, користуючись графіком. Навчити досліджувати функцію на парність та монотонність і неперервність на заданому відрізку. Розвивати просторову уяву, логічне мислення, виховувати акуратність та зосередженість при виконанні досліджень та побудові графіків.

Теоретична частина

Функція та її властивості. Функцією називається залежність змінної у від змінної х, якщо кожному значенню х відповідає єдине значення у.

Позначення: , де х – незалежна змінна (аргумент); у – залежна змінна (функція) .

Множина значень, яких набуває змінна х називається областю визначення функції. Позначення

Множина значень залежної змінної у, яких вона набуває при всіх значеннях х  називається областю значень функції. Позначення:

а) Яка область визначення функцій, графіки яких зображено на рис. ?

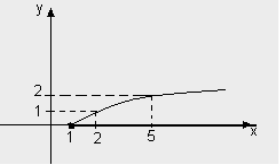
Область визначення функції - це проміжок , тому, що вираз має зміст при , тобто  .

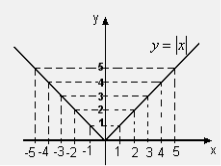
Область визначення функції - вся координатна пряма .

б) Яка область значень функцій, графіки яких зображено на рис. ?

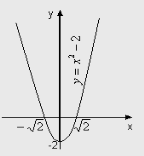
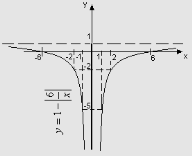
Область значень функції множина  .

Область значень функції множина .

Зростання, спадання, парність та непарність  функції.

Якщо для  будь-яких  двох  значень аргументу більшому значенню аргументу відповідає більше  значення функції, то таку функцію називають зростаючою.

( ).  Рис 1.

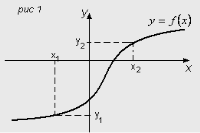
Якщо для  будь-яких двох значень аргументу більшому значенню аргументу відповідає менше значення функції, то таку функцію називають спадною.

( ).  Рис 2

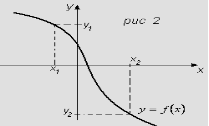
Функція називається парною, якщо для  будь-яких двох протилежних значень аргументу отримуємо  рівні значення  функції, тобто . Графік парної функції симетричний відносно осі  Оу.

 Приклад. Функція є парною:

 . Рис 3  

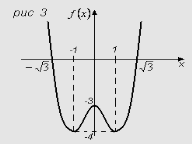
Функція  називається  непарною, якщо для будь-яких двох протилежних значень аргументу отримуємо протилежні значення функції, тобто . Графік непарної функції симетричний відносно початку координат.

Приклад. Функція є непарною:

. Рис 4

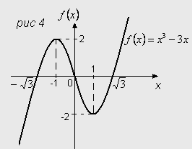
Велика кількість функцій не належить ні до парних ні до непарних. Прикладом такої функції є функція . Рис 5

 .

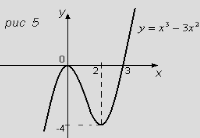
Приклад. Знайти область визначення  функцій: .

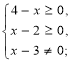
Розв'язання. Арифметичний корінь існує лише для невід'ємних чисел, дріб існує при . Маємо    

Відповідь: .

Завдання для самоконтролю