Тема „Найбільше, найменше значення функції”

Тема „Найбільше, найменше значення функції”

 

Мета:  продовжувати формувати вміння розв'язувати задачі назнаходження найбільшого (найменшого) значення величин, уміння знаходити найбільшого (найменшого) значення функції на відрізку, формувати вміння знаходити найбільшого (найменшого) значення функції на заданому інтервалі по графіку цієї функції та вміння перевіряти правильність результатів, одержаних в результаті аналітичних розрахунків.

Розвивати логічне мислення, математичну мову, вміння використовувати набуті знання та вміння при розв'язувані задач практичного змісту, навички роботи з ППЗ GRAN1.

Виховувати навички роботи в команді, інтерес до предмету.

 

Обладнання: таблиці: „Похідні елементарних функцій”, „Точкиекстремуму”, „Знаходження найбільшого та найменшого значення функції на відрізку”, „Найбільшого (найменшого) значення функції на відкритому інтервалі”, графік залежності економічного розвитку від часу, схема до задачі, ППЗ GRAN1, картки, епіграф уроку.

 

Хід уроку

І  Організація класу

 

II  Мотивація навчання

„Для життя, а не для школи ми вчимося” — Ці слова є епіграфом нашого уроку. Переконаємося в цьому зараз.

 

Повідомляється тема уроку та завдання на урок.

 

1. Розв'язувати задачі на знаходження найбільшого (найменшого)

значення величин аналітично.

2. Знаходити найбільше (найменше) значення функції на відрізку

аналітично.

3. Використовуючи ППЗ GRAN1, визначити найбільше (найменше)

значення функції по її графіку та виконати перевірку аналітичних результатів.

 

-   Якщо ви уявите себе економістами, то ви повинні вміти аналізувати залежність економічного розвитку від часу. (Демонструється відповідний графік).

-    З точки зору математики точки „бумів” та „криз” є ...? (Точки локальних екстремумів функції, що виражає цю залежність.)

-    А можемо ми проаналізувати, чи є точки Б₂, К₂ найбільшим та найменшим показниками економічного розвитку у період часу від до ? (Так.)

-    Як це зробити ? (Знайти найбільше та найменше значення функції Е(t) на і порівняти їх із значеннями Б₂, К₂)

-    Отже потрібно розв'язати задачу математичного аналізу.

 

 

 

III  Розв'язування задачі практичного змісту

 

Які знання теорії необхідні для розв'язання задач на знаходження найбільшого (найменшого) значення?

 

Учні самостійно повідомляють теоретичні питання.

 

1. Правило знаходження найбільшого (найменшого) значення неперервної функції на відрізку.

 

2. Розв'язуючи задачі на знаходження найбільшого (найменшого) значення величини потрібно?

 

•    Ту величину, найбільше (найменше) значення якої треба знайти, приймають за у (або як зручно).

•     Одну з невідомих величин позначити за х і встановити реальні межі зміни х в залежності від умови задачі.

•    Виразити у через х. Таким чином одержати функцію у=f(х).

•    Знайти найбільше (найменше) значення функції на визначеному проміжку для х

.

Розв'яжемо задачу

 

В степу, на відстані 9 км на північ від шосе, яке тягнеться з заходу на схід, знаходиться пошукова партія. На відстані 15 км на схід від найближчої до пошукової партії точки, що лежить на шосе, знаходиться райцентр.

З пошукової партії виїжджає кур'єр на велосипеді в райцентр. Який повинен бути маршрут руху кур'єра, щоб він прибув в райцентр найшвидше. Якщо по степу він їде з швидкістю 8 км/год, а по шосе — 10 км/год.

 

Аналізується умова, виконується малюнок.

Після цього підготовлений малюнок до умови задачі.

 Розв'язання:

1. y — t_найм

2. АМ = х км,       хє [0;15]

 

3.

t_PM=; t_PM== ;

МВ= 15-х;  t_MB==(15-x);

t=(15-x);

;

, оскільки  81+х² > 0 ;

25х²=16·81+16х²;

 9х²=16·81;

 х²=16·9;

х=12;

— найменше;

x=12 км;

BM=3 км.

Відповідь: BM=3 км.

 

IV Робота в комп'ютерному класі

• Друга частина уроку пройде в комп'ютерному класі.
• Виконаємо наступне завдання уроку - знайдемо найменше значення функції t(х), де х є [0; 15] та відповідне значення х_найм, побудувавши графік цієї функції. Використаємо для цього ППЗ GRAN1.
• Нагадую правила запису математичних виразів відповідні записи на дошці

— sqrt(x)

2x² — 2*(x^2)  

— (x+1)/(x-2)

 

• Відрізок задаєте А=0 ; В = 15.

 

•  Який результат отримали          Унайм ⁼ У(      )    (учні будують графік і визначають найменше у).

 

• Так можна перевірити аналітичні розрахунки .

 

• Наступний етап уроку - це робота в командах.

 

V Самостійна робота учнів в командах

 

Кожна команда із 2,3 учнів отримує завдання (завдання різних рівнів).

 

Завдання командам

• Розв'язати завдання аналітично і перевірити правильність результату графічно.
• Один учень з команди захищає виконану роботу.

• Інший - відповідає на питання з теорії, вибране, як білет на екзамені.
• Команда оцінюється, враховуючи правильність, самостійність виконання, роботу кожного учня та рівень завдання.

 

Команда 1       (7балів)

 

Знайдіть найбільше та найменше значення функції у = 2х³-15х²+36х- 13,     хє[-0,5;3]

 

Розв'язання:

1. у' = 6х² - ЗОх + 36;

у' = 0; 6х²-ЗОх+ 36 = 0; х² - 5х + 6 = 0;

х₁ = 3; х₂ = 2.

 

2. у(-0,5)= -35;

    у(2)=15;

     у(3)=14;

унайм.=у(-0,5)= -35;

унайб.=у(3)=14

 

Команда 2        (8балів)

 

Парканом, довжина якого 80м, огородити ділянку найбільшої площі.

 

Розв'язання:

1. Р_пр=80м;  Sнайб-?   a, b -?

Нехай а = х;        b = 40 - х;

S=ab;    у=S(x);

S = х(40 - х ) = 40х - х², х є (0;40)

Унайб ~ ?

S' = 40 - 2х;

S'=0;  40-2x=0;   

х = 20є (0;40); S'(10) >0; S'(30)<0;

отже у_mах(20) = 400м² = у_найб

Відповідь: 20x20.

 

Команда 3_________(9балів)

 

Знайти найбільше і найменше значення функцій                        

У= хє[0;5]

 

Розв'язання:

1.

              

=

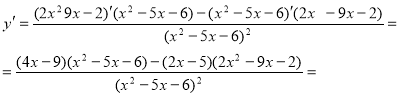
y'=0;     -x

(x

x

x

x

2.. y(0)=1/3;

у(2) = (2*4-9*2-2) / (4-10-6) = 1 ; у(5) = (2*25-45-2)/(25-25-6) = -0,5;

 

Команда 4_________(12балів)

 

Знайти сторони рівнобедреного трикутника з периметром р, площа якого найбільша.

 

Розв'язання:

Нехай х - бічна сторона, тоді   р - 2х — основа х є (0; р/2)

S=h(х-2p);

h= =;

S=хє(0;p/2);

1.S’= -+;

S’=0;

4px-p>0,

p-2px=4px-p;

3px=p;

x=p/3.

 

2. При переході через p/3  функція S(x) міняє знак з “+” на “-“, отже 

Sнайб=Smax(p/3)

 

Відповідь: рівносторонній трикутник.

 

 

 

Питання теорії:

1. Алгоритм знаходження найбільшого (найменшого) значення функції.

2. Ознака зростання функції на проміжку.

3. Точки екстремуму.

4. Стаціонарні точки.

VII Підсумок уроку

Повторіть як розв'язується задача на знаходження найбільшого (найменшого) значення величин. Д.З. рVПІ, №5(2,3,4)

 

Задача: потрібно виготовити скриньку без кришки з прямокутною основою та заданим об'ємом V, у якої б відношення сторін основи дорівнює к. Якими повинні бути розміри скриньки, щоб її поверхня була найменшою?

найбільша.