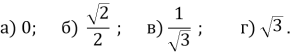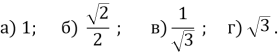Тема Основні співвідношення між тригонометричними функціями одного аргументу
Тема Основні співвідношення між тригонометричними функціями одного аргументу.
Мета
Навчальна: вивчити співвідношення між тригонометричними функціями одного аргументу, сформувати уміння застосовувати вивчені співвідношення для тотожних перетворень (спрощення) виразів, навчитися знаходити значення тригонометричних функцій за однією відомою функцією.
Розвиваюча: розвивати уважність, працелюбність, навички творчого застосування знань до виконання вправ;
Виховна: виховувати інтерес до предмету, культуру ведення записів як на дошці, так і в зошитах.
Тип уроку: комбінований.
Методи і прийоми: розв’язування кросворду, використання слайдів, перегляд презентації.
Обладнання: комп’ютер, мультимедійний проектор, презентація у Power Point, картки-завдання, кросворд.
Міжпредметні зв’язки: фізика, медицина, астрономія.
Література:
1. Бевз Г.П. Математика: 10: підруч. для загальноосвіт. навч. закл. : рівень стандарту/ Г.П.Бевз, В.Г.Бевз. – К.: Освіта, 2018. -288с.
2. А.П. Єршова, В.В. Голобородько. Геометрія 10-11 кл. (Самостійні та контрольні роботи) „Гімназія” Харків. „Олекса” Москва 2003.
3. Мерзляк А.Г., Полонський В.Б., Рабінович Ю.М., Якір М.С. Збірник задач і завдань для тематичного оцінювання з алгебри і початків аналізу для 10 класу. – Харків, Гімназія, 2001. – 112 с.: іл.
Епіграф уроку: «Знання лише тоді знання, коли воно отримане зусиллям розуму, а не пам’яті» (Слайд 1)
Л.М.Толстой.
Хід уроку
І. Організаційний момент. Вітаюся з учнями, відмічаю відсутніх, записуємо число, класна робота.
ІІ. Перевірка домашнього завдання
Викладач перевіряє наявність домашнього завдання та дає відповіді на запитання учнів, які виникали при його виконанні. Учні звіряють розв’язок вправ з відповіддю на екрані. (Слайд2)
№227. Обчисліть:
№264. Запишіть![]()
![]()
![]()
ІІІ. Актуалізація опорних знань.
Викладач Видатний письменник Л.М. Товстий говорив: «Знання лише тоді знання, коли воно отримане зусиллям розуму, а не пам’яті». От і ми на сьогоднішньому відкритому уроці будемо тренувати свою розумову діяльність. Вашу готовність до сьогоднішнього уроку давайте перевіримо за допомогою написання тестових завдань і розв’язування кросворду
Учні одного ряду виконують тестові завдання на картках:
|
Варіант 1
1. Чому дорівнює
2. Чому дорівнює
3. Обчисліть:
4. Чому дорівнює
5. Запишіть у радіанній мірі кути:
6. Виразіть у градусах кут, радіанна міра якого дорівнює даному числу:
|
Варіант 2
1. Чому дорівнює
2. Чому дорівнює
3. Обчисліть:
4. Чому дорівнює
5. Запишіть у радіанній мірі кути:
6. Виразіть у градусах кут, радіанна міра якого дорівнює даному числу:
|
Два ряди давайте повторимо те, що ми вивчили на минулих заняттях
Розгадайте кросворд (Слайд3)
По горизонталі:
- Синус та косинус у першій чверті має знак …..
-
Кут, який дорівнює 90
 називається ….
називається ….
- Геометрична фігура, утворена двома променями, які виходять з однієї точки.
- Відношення довжини прилеглого катета до довжини протилежного катета.
- Розділ математики, що вивчає співвідношення між сторонами й кутами трикутників.
- Відношення довжини протилежного катета до довжини прилеглого катета.
- Відношення довжини протилежного катета до довжини гіпотенузи.
По вертикалі:
- Відношення довжини прилеглого катета до довжини гіпотенузи.
-
Кут, який дорівнює 180
 називається….
називається….
- Синус у третій та четвертій чверті має знак …..
- Центральний кут, довжина дуги якого дорівнює радіусу цієї дуг.
-
Одна з координат точки в Декартові системі координат, що позначає величину на осі
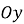 .
.
- Одиниця вимірювання кутів.
-
Одна з координат точки в Декартові системі координат, що позначає величину на осі
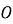
|
|
К |
|
|
|
|
|
|||||||||||||
|
Д |
О |
Д |
А |
Т |
Н |
і |
Й |
||||||||||||
|
|
С |
|
|
|
|
||||||||||||||
|
|
П |
Р |
Я |
М |
И |
Й |
|||||||||||||
|
|
О |
|
Н |
|
В |
|
|
|
|||||||||||
|
З |
|
К |
У |
Т |
|
І |
Р |
||||||||||||
|
К |
О |
Т |
А |
Н |
Г |
Е |
Н |
С |
|
Д |
|
А |
О |
||||||
|
|
О |
|
Є |
Д |
Р |
||||||||||||||
|
Т |
Р |
И |
Г |
О |
Н |
О |
М |
Е |
Т |
Р |
І |
Я |
Д |
||||||
|
|
Н |
|
Р |
|
|
|
Н |
|
А |
|
И |
||||||||
|
У |
А |
И |
|
Т |
А |
Н |
Г |
Е |
Н |
С |
|||||||||
|
Т |
Д |
Й |
|
Б |
|
А |
|
||||||||||||
|
С |
И |
Н |
У |
С |
|
С |
Т |
||||||||||||
|
|
Й |
|
С |
|
|
Ц |
А |
||||||||||||
|
|
И |
|
|||||||||||||||||
|
|
|
|
|
С |
|||||||||||||||
|
|
А |
|
|||||||||||||||||
І V. Повідомлення теми, мети заняття. Мотивація навчальної діяльності. Тема нашого уроку «Співвідношення між тригонометричними функціями одного й того самого аргументу». Це означає, що на цьому уроці ми пригадаємо основну тригонометричну тотожність, відому вам з курсу геометрії 9-го класу, а також низку формул, які пов’язують дані тригонометричні функції одного аргументу, навчимося використовувати дані співвідношення при розв’язуванні вправ та задач.
V.Вивчення нового матеріалу.
На минулому уроці ми з вами розглянули таблицю значень тригонометричних функцій різних кутів. Сьогодні я хочу показати ще один метод знаходження значень синусів цих кутів.
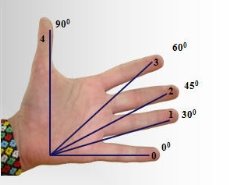 Використовуємо ліву руку
Використовуємо ліву руку
Загальна формула для знаходження значення синуса кута
![]()
Де ![]() - номер пальця. (Слайд 4)
- номер пальця. (Слайд 4)
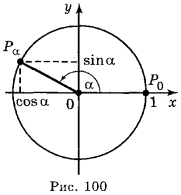 Співвідношення між синусом і косинусом.
Співвідношення між синусом і косинусом.
Нехай точка Ρα (х, у) одиничного кола отримана поворотом точки Р0(1; 0) на кут α радіан, тоді згідно з означенням синуса і косинуса:
х = cos α, у = sin α (рис. 100)
Оскільки точка Рα(х;у) належить одиничному колу, то координати (х; у) задовольняють рівнянню х2 + у2 = 1. Підставивши в це рівняння замість х і у значення cos α і sin α , отримаємо:
![]()
![]()
Таким чином, ![]() для всіх значень α. Ця рівність називається основною тригонометричною тотожністю.
для всіх значень α. Ця рівність називається основною тригонометричною тотожністю.
З основної тригонометричної тотожності можна виразити sin α через cos α і навпаки.
![]()
![]()
![]() (Слайд 5)
(Слайд 5)
Співвідношення між тангенсом і котангенсом.
Згідно з визначенням тангенса і котангенса
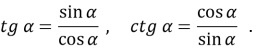
Перемноживши ці рівності, одержимо
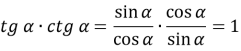
Отже, ![]() для всіх значень α, де існують ці тригонометричні функції.
для всіх значень α, де існують ці тригонометричні функції.
Із одержаної рівності можна виразити![]() через
через ![]() і навпаки:
і навпаки:
![]() (слайд6)
(слайд6)
Приклади застосування основних співвідношень між тригонометричними функціями одного аргументу
-
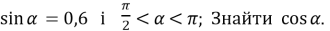 ,
,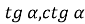 .(Слайд7)
.(Слайд7)
![]()
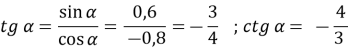
2)![]()
![]()
VІ.Закріплення вивченого матеріалу.
Робота за підручником «Математика» 10 Г.П.Бевз, 2019 (Слайд 8)
№ 297,299, 300, 303.
№297. Доведіть тотожність
a) ![]()
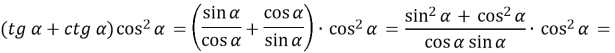
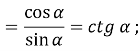
№299. Спростіть вираз:
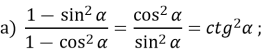
№300. Відомо, що кут ![]() гострий. Обчисліть значення:
гострий. Обчисліть значення:
а)![]()
![]()
№303. Спростіть вираз:
![]()
Самостійна робота (з подальшою взаємоперевіркою)
Метою кожного уроку є підготовка до ЗНО, що містить тестові завдання. Саме зараз ми розв’яжемо такі. Я пропоную Вам два варіанти, у кожному з яких три завдання, що мають чотири варіанти відповідей. Ви розв’язуєте їх самостійно (Слайд 9)
Варіант 1 Варіант 2
- Знайти значення виразу: 1. Знайти значення виразу
![]()
А)1; Б) -1; В) 19; Г) -9 А)0; Б) -6; В) 5; Г) 1
2.Cпростити вираз: 2. Cпростити вираз:
sin![]()
А)2cos![]()
3.Знайти cos![]() , якщо
, якщо ![]() якщо
якщо
![]()
![]() cos
cos![]()
А)![]()
Розв’язання
|
Варіант1
1.
Відповідь: Б
2.
Відповідь: А
3.
cos
Відповідь: Г |
Варіант 2
1.3
Відповідь:А
2.cos
Відповідь:В
3.sin
sin
Відповідь:Б |
VІІ. Тригонометрія в науці і житті (Слайд 10)
Тригонометрія застосовується не лише в математиці, а і у фізиці, астрономії, медицині та інших галузях.
За допомогою тригонометричних функцій описується багато процесів у природі: коливання струни, маятника, звукові коливання, напруга і струм в ланцюзі змінного струму.
Поява веселки пояснюється законом заломлення світла ![]() =n, де n- відносний показник заломлення середовища,
=n, де n- відносний показник заломлення середовища, ![]() ,
, ![]() – кут заломлення світла.
– кут заломлення світла.
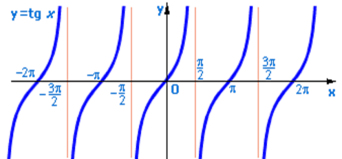
Якщо на хвості риби зафіксувати точку, то можна розглянути траєкторію руху, яка нагадує косинусоїду чи синусоїду, а при плаванні тіло риби приймає форму кривої яка нагадує графік функції у=tgx.

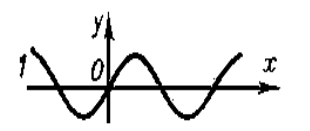
При польоті птахів траєкторія змаху крил утворює синусоїду

В архітектурі: ресторан в Лос-Манантіалісі, виноробня “Бодегас Ісіос”(Іспанія), дитяча школа в Барселоні, страхова корпорація в Лондоні.
У хореографії інколи є такий рух як хвиля, що нагадує синусоїду чи косинусоїду.
VІІІ. Підведення підсумків.
Сьогодні на уроці ми вивчили співвідношення між тригонометричними функціями одного аргументу, сформували уміння застосовувати вивчені співвідношення для тотожних перетворень (спрощення) виразів, навчилися знаходити значення тригонометричних функцій за однією відомою функцією.
ІХ. Оцінювання знань учнів
Виставлення і коментування оцінок.
Х. Домашнє завдання.
Завдання за підручником «Математика» 10 Г.П.Бевз, 2018.
§8 Розв’язати:№296 (б), №298 (а, б) , №302(а)
1


про публікацію авторської розробки
Додати розробку