Тема: Похідна функції. Знаходження похідних функцій
Тема: Похідна функції. Знаходження похідних функцій
Мета:
навчальна: сформувати вміння знаходити похідні функцій, використовуючи правила знаходження похідних;
розвивальна: розвивати логічне мислення, комунікабельність, увагу, пам’ять, здатність до самостійності мислення; усне та писемне мовлення; розвивати інтерес до математики;
виховна: виховувати в учнів бажання мати глибокі й міцні знання, працьовитість та уважність; сприяти розвитку всесторонньо розвинутої особистості;
Теоретична частина
1. Означення похідної функції
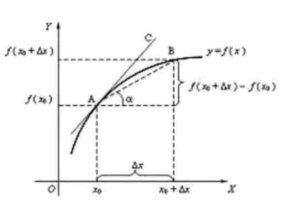
Нехай задано функцію y=f(x) на деякому проміжку. Візьмемо довільну
внутрішню точку x0 цього проміжку, надамо значенню х0 довільного приросту Δ x (число Δх може бути як додатним, так і від’ємним), але такого, щоб точка х 0+Δх належала даному проміжку.
Тоді
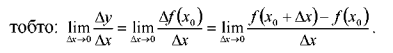
Якщо дана границя існує, то її називають похідною функції y=f(x) у точці 
і позначають
або у'.
Похідною функції y=f (x) у точці х0 називають границю відношення приросту функції до приросту аргументу за умови, що приріст аргументу
прямує до нуля, а границя існує, тобто
Функцію, яка має похідну в точці
називають диференційованою в цій точці. Функцію, яка має похідну в кожній точці деякого проміжку, називають диференційованою на цьому проміжку. Операція знаходження похідної називається диференціюванням.
2. Таблиця похідних елементарних функцій
Це формули за допомогою яких знаходять похідні даних функцій.
Кожна з цих формул доведена у XVII ст.
3. Правила диференціювання
Теорема 1. (Похідна суми функцій) Якщо функції u(x) та v(x) диференційовані в точці x, то в цій точці буде диференційованою і сума цих функцій. Причому, похідна суми функцій дорівнює сумі похідних від цих
функцій, тобто
Приклад 1. Знайти похідну функції y = 2 - x + x2.
Розв’язання:
Теорема 2. (Похідна добутку функцій) Якщо функції u(x) та v(x) диференційовані в точці x, то в цій точці буде диференційований добуток цих функцій і має місце формула
Приклад 2. Знайти похідну функції
Розв’язання:
Наслідок 1. Cталий множник можна виносити за знак похідної
Приклад 3. Знайти похідну функції y = 5tgx. Розв’язання:
Наслідок 2. Похідна добутку декількох диференційованих функцій дорівнює сумі добутків похідної кожного з цих множників на всі інші.
, де u, v, w - диференційовані функції.
Приклад 4. Знайти похідну функції
Розв’язання:
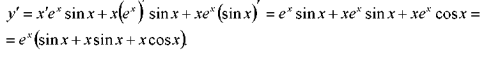
Теорема 3. (Похідна частки функцій) Якщо функції u(x) та v(x) диференційовані в точці x і v(x)*0, то частка цих функцій також
диференційована в точці x і має місце формула
Приклад 5. Знайти похідну функції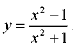
Розв’язання:
Наслідок 3.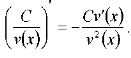
Приклад 6. Знайти похідну функції
Розв’язання: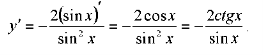
Завдання для самоконтролю
Вивчити п. 8 (Г.П. Бевз, В.Г. Бевз Математика 11 клас, Київ «Генеза» 2011)
№ 267 – а, б, г, д;
№ 271, № 275 – а, б, в.
про публікацію авторської розробки
Додати розробку