Тема: Похідна складеної функції.

Тема: Похідна складеної функції.

Мета:

навчальна: навчити студентів знаходити похідну складеної функції, використовуючи здобуті раніше знання; розкрити поняття складної функції, навчити студентів розрізняти складну функцію від простої;

розвиваюча: розвивати самостійність мислення студентів, розвивати логічне мислення, вміння концентрувати увагу, аналізувати, узагальнювати, розвивати інтерес до предмету.

Теоретична частина

1.                   Сприймання і усвідомлення поняття складеної функції та її похідної.

Якщо значеннями аргументу функції є значення функції , то говорять, що задано складену функцію .

Наприклад, розглянемо функції і , де і . Тоді

 .

 Отже, можна говорити, що формула задає складену функцію .

Розглянемо ще кілька прикладів. Якщо , а , то складена функція задається формулою . Функцію можна розглядати як складену функцію  , де , .

Знаходити похідну складеної функції можна за допомогою такої теореми.

Теорема (похідна складеної функції). Якщо функція диференційована в точці , а функція диференційована в точці , де , то складена функція є диференційованою в точці , причому

.

2. Таблиця похідних

Практична частина

Розглянемо деякі приклади.

Приклад 1.

зовнішня функція - , внутрішня -     

Приклад 2.

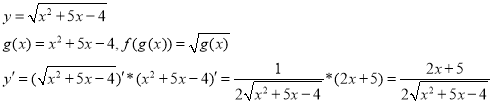
Приклад 3.

Приклад 4.

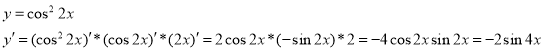
Приклад 5.

Приклад 6.

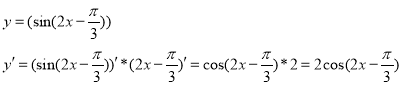
Приклад 7.

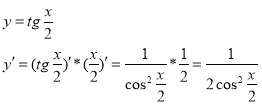
Приклад 8.

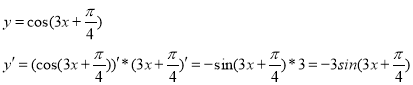
Приклад 9.

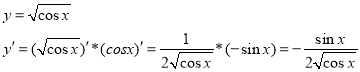
Приклад 10.

Приклад 11.

 Приклад 12.

Завдання для самоконтролю

Знайдіть похідні функцій: