Тема: Розв’язування ірраціональних рівнянь
Тема: Розв’язування ірраціональних рівнянь
Формування компетентностей:
предметна компетентність: удосконалити вміння й навички розв’язувати ірраціональні рівняння, повторити вивчені методи, розширити знання новими нестандартними методами розв’язування ірраціональних рівнянь; розвивати пам’ять, логічне мислення, пізнавальний інтерес до математики;
ключові компетентності: спілкування державною мовою - чітко, лаконічно та зрозуміло формулювати думку; уміння вчитися впродовж життя – відбирати і застосувати потрібні знання для досягнення мети;
соціальна та громадська компетентності – аргументувати та відстоювати свою позицію, етику та культуру спілкування, виховувати навички взаємопідтримки та взаємодопомоги.
Тип уроку: удосконалення знань, умінь і навичок
Обладнання: екран, діапроектор, роздатковий матеріал.
Хід уроку:
І. Організаційний етап. Повідомлення теми і мети уроку
Учні записують у зошит дату й тему уроку. (заздалегідь написано на дошці)
Учитель повідомляє мету уроку, налаштовує учнів на роботу.
ІІ. Перевірка домашнього завдання
№ 7.3 1) х=67; 2)х=-15; 3) розв’язків не має.
№ 7.5 1) х=6; 2) коренів не має;
№7.7 1) х=-5; 2) х=4; 3)х=-1; 4) х=5.
ІІ. Актуалізація опорних знань
Історична довідка
Поняття ірраціональності асоціюється завжди із зображенням кореня. Знак кореня з’явився у 1525 році. До нашого часу його зображення змінювалось. Хто ж вперше ввів це зображення? Про це ви дізнаєтесь, розгадавши кросворд (слайд).
Запитання:
-
Скільки розв’язків має рівняння
? (один)
- Корінь якого степеня існує із будь-якого числа? (непарного)
- Як називають корінь третього степеня? (кубічний)
-
Скільки розв’язків має рівняння
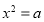, якщо a >0? (два)
- Як називається рівняння, в якому змінна знаходиться під знаком кореня? (ірраціональне)
- Як називається корінь рівняння, який одержується в результаті нерівносильних перетворень? (сторонній).
Завдання
Введіть відповіді на запитання (запитання на слайді) у відповідні комірки електронної таблиці і дізнайтеся ключове слово (Рене Декарт).
Переходимо до бліц-опитування
Завдання 1. Увага на екран. Знайдіть, будь-ласка, серед запропонованих рівнянь ірраціональні:
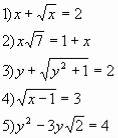
Завдання 2. Чи являється число коренем рівняння:
1) 
, 
2) 
, 
Завдання 3. Знайдіть корені рівняння:
1) 
2) 
3) 
4) 
Висновок: повторено означення ірраціонального рівняння, коренів рівняння, властивості кореня n-го степеня та розв’язування найпростіших ірраціональних рівнянь.
IІІ. Удосконалення знань
1. Тестування
Для перевірки готовності до уроку пропоную пройти тестування на роздрукованих листочках.
Тести. 1. Обчислити: 
а) 4; б) 2; в) 0,5; г) 8
2. Обчислити: 
а) -2; б) -
; в) 34; г) розв’язку немає
3. При яких значеннях х вираз має зміст: 
а) 
; б) 
; в) 
; г) 
4. Розв’язати рівняння: 
а) 4; б) 2; в) 16; г) -2
5. Розв’язати рівняння: 
а) 11; б) 21; в) -16; г) 121
6. Розв’язати рівняння: 
а) 2; б) 265; в) -265; г) коренів немає
7. Розв’язати рівняння: 
а) 1; -3,5; б) 1; 3,5; в) -1; г) -1; -3,5.
Відповіді:
|
№ 1 |
№ 2 |
№ 3 |
№ 4 |
№ 5 |
№ 6 |
№ 7 |
|
б |
г |
в |
а |
г |
г |
г |
2. Фронтальна робота
Нестандартні методи розв’язування ірраціональних рівнянь
Метод рівносильних перетворень
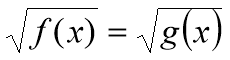
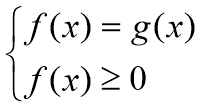
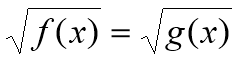
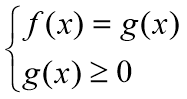
Повторення вивчених методів розв’язування ірраціональних рівнянь
- Піднесення обох частин рівняння до одного степеня.
- Заміна змінної в рівнянні.
- Розкладання на множники.
- Врахування області визначення функції.
- Графічний метод.
Приклад рівняння на заміну змінних до пункту 2):
Робим заміну: 
, тоді 
,
Одержуєм рівняння: 
розв’язків не має;
, х=2 - розв’язок.
Відповідь: х=2.
Приклад рівняння розкладання на множники до пункту 3):
Розв’язання: 
Відповідь: 
.
Приклад на врахування області визначення до пункту 4)
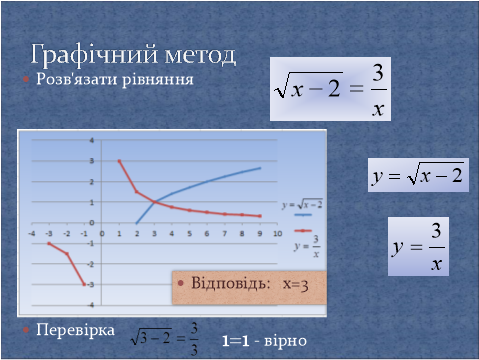
Приклад графічного розв’язання ірраціонального рівняння до пункту 5):
Завдання. Поставити у відповідність записаному рівнянню номер метода, який застосовується для його розв’язання.
Варіант І
Виберіть метод розв’язування даного ірраціонального рівняння:
- піднесення до степеня;
- заміна змінної;
- розкладання на множники;
-
використання властивостей функції
;
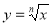- графічний.
|
Рівняння |
Методи розв’язування |
||||
|
|
1 |
2 |
3 |
4 |
5 |
|
1) |
|
|
|
|
|
|
2) |
|
|
|
|
|
|
3) |
|
|
|
|
|
|
4) |
|
|
|
|
|
|
5) |
|
|
|
|
|
Варіант ІІ
Виберіть метод розв’язування даного ірраціонального рівняння:
1)піднесення до степеня;
2)заміна змінної;
3)розкладання на множники;
4) використання властивостей функції ;
5)графічний.
|
Рівняння |
Методи розв’язування |
||||
|
|
1 |
2 |
3 |
4 |
5 |
|
1) |
|
|
|
|
|
|
2) |
|
|
|
|
|
|
3) |
|
|
|
|
|
|
4) |
|
|
|
|
|
|
5) |
|
|
|
|
|
Відповіді:
Варіант І
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
|
+ |
|
|
|
|
2 |
|
|
+ |
|
|
|
3 |
+ |
|
|
|
|
|
4 |
|
|
|
|
+ |
|
5 |
|
|
|
+ |
|
Варіант 2
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
+ |
|
|
|
|
|
2 |
|
+ |
|
|
|
|
3 |
|
|
|
+ |
|
|
4 |
|
|
|
|
+ |
|
5 |
|
|
+ |
|
|
Проаналізувавши дані завдання можна прийти до висновку, що при розв’язуванні будь-якого ірраціонального рівняння треба застосовувати метод «пильного погляду», тобто спочатку треба уважно роздивитись і проаналізувати умову рівняння, а потім уже визначатись з методом розв’язання.
Наприклад, до 3-го рівняння на перший погляд можна застосувати метод піднесення обох частин до степеня. Але це приводить до громіздких записів. Витрачається багато часу на розв’язання.
«Пильним поглядом» розглянувши умову, ми бачимо, що область визначення функції
y =
: 
, а y =
: 
, тому тут доречно знайти область визначення функції, яка стоїть в лівій частині:
- 5
х є О
Отже, ліва частина не існує ні при одному значенні х. Таким чином, питання про розв’язок рівняння знімається
4 рівняння 
розв’язується графічно. Побудувавши графіки функцій 
і 
в одній системі координат, ми отримаємо точку перетину, абсциса якої і є розв’язком рівняння: х=3
Враховуючи, що точність побудови графіків може бути порушена, треба обов’язково зробити для себе перевірку:
1=1 – вірно.
У першому рівнянні 
в лівій і правій частинах корінь другого степеня, тому використовуємо метод піднесення до степеня.
Показники коренів другого рівняння 
2 і 4, 4 у 2 рази більше, ніж 2. Тому треба ввести нову змінну і прийти до квадратного рівняння.
У 5 рівнянні присутній однаковий множник 
, який треба винести за дужки і розкласти ліву частину на множники.
Таким чином, метод «пильного погляду» дуже допомагає нам при розв’язуванні ірраціональних рівнянь.
ІV. Застосування знань та вмінь
-
Розв’яжіть рівняння:
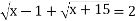
Розв’язання: х-1+
=4, 
Відповідь: х=1.
-
Розв’яжіть рівняння:
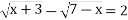
Розв’язання: ОДЗ: х+3 ≥ 0; 7-х ≥ 0; х ≥ -3; х ≤ 7.
(х+3)(7-х)=9; 
Відповідь: 
4. Завдання. В групах розв’язати рівняння методом «пильного погляду».
1. 
+
- рівняння розв’язків не має;
2. 
- єдиний розв’язок х=3.
6. Самостійна робота
Варіант 1
№1. Розв’яжіть рівняння 
.
|
1) |
15 |
3) |
12 |
|
2) |
17 |
4) |
4 |
№2. Розв’яжіть рівняння 
і вкажіть найменший корінь
|
1) |
6 |
3) |
-5 |
|
2) |
5 |
4) |
-6 |
Варіант 2
№1. Розв’яжіть рівняння 
.
|
1) |
4 |
3) |
-1 |
|
2) |
3 |
4) |
9 |
№2. Розв’яжіть рівняння 
|
1) |
26 |
3) |
-1 |
|
2) |
-3 |
4) |
0 |
№2. Розв’яжіть рівняння і вкажіть найменший корінь
Розв’язання: 
№2. Розв’яжіть рівняння
Розв’язання: 
Відповідь: х=0 – розв’язок.
Увага на екран! Перевірте свої розв’язки.
Відповіді:
|
|
|
|
|
Варіант 1 |
17 |
-5 |
|
Варіант 2 |
3 |
0 |
V. Домашнє завдання: параграф 7; №7.9; 7.11; 7.14.
VІ. Підведення підсумків. Оцінювання діяльності учнів
Притча:
Ішов Мудрець, а назустріч йому три чоловіки, які везли під гарячим сонцем візки з камінням для будівництва. Мудрець зупинився і задав кожному запитання. У першого запитав «Що ти робив цілий день?». І той відповів, що цілий день возив це важке каміння. У другого запитав мудрець «А що ти робив цілий день?», і той відповів: «А я добросовісно виконував свою роботу». А третій посміхнувся, його обличчя засвітилося радістю і задоволенням: « А я приймав участь у будівництві храму!»
І ми сьогодні на уроці приймали участь у будівництві храму – храму науки.
Бажаю всім ще кращих результатів. Дякую за роботу
Тести. 1. Обчислити:
а) 4; б) 2; в) 0,5; г) 8
2. Обчислити:
а) -2; б) -; в) 34; г) розв’язку немає
3. При яких значеннях х вираз має зміст:
а) ; б) ; в) ; г)
4. Розв’язати рівняння: а) 4; б) 2; в) 16; г) -2
5. Розв’язати рівняння:
а) 11; б) 21; в) -16; г) 121
6. Розв’язати рівняння:
а) 2; б) 265; в) -265; г) коренів немає
7. Розв’язати рівняння:
а) 1; -3,5; б) 1; 3,5; в) -1; г) -1; -3,5.
Тести. 1. Обчислити:
а) 4; б) 2; в) 0,5; г) 8
2. Обчислити:
а) -2; б) -; в) 34; г) розв’язку немає
3. При яких значеннях х вираз має зміст:
а) ; б) ; в) ; г)
4. Розв’язати рівняння: а) 4; б) 2; в) 16; г) -2
5. Розв’язати рівняння:
а) 11; б) 21; в) -16; г) 121
6. Розв’язати рівняння:
а) 2; б) 265; в) -265; г) коренів немає
7. Розв’язати рівняння:
а) 1; -3,5; б) 1; 3,5; в) -1; г) -1; -3,5.
Самостійна робота
Варіант №1.
№1. Розв’яжіть рівняння:
варіанти відповіді: 1)15; 2) 17; 3) 12; 4) 4.
№2. Розв’яжіть рівняння:
і вкажіть найменший корінь рівняння
Варіанти відповіді: 1) 6; 2) 5; 3) -5; 4)-6;
Самостійна робота
Варіант №2.
№1. Розв’яжіть рівняння: 
Варіанти відповіді: 1) 4; 2) 3; 3) -1; 4) 9;
№2. Розв’яжіть рівняння: 
Варіанти відповіді: 1) 26; 2) -3; 3)-1; 4) 0.
Самостійна робота
Варіант №1.
№1. Розв’яжіть рівняння:
варіанти відповіді: 1)15; 2) 17; 3) 12; 4) 4.
№2. Розв’яжіть рівняння:
і вкажіть найменший корінь рівняння
Варіанти відповіді: 1) 6; 2) 5; 3) -5; 4)-6;
Самостійна робота
Варіант №2.
№1. Розв’яжіть рівняння:
Варіанти відповіді: 1) 4; 2) 3; 3) -1; 4) 9;
№2. Розв’яжіть рівняння:
Варіанти відповіді: 1) 26; 2) -3; 3)-1; 4) 0.
Самостійна робота
Варіант №1.
№1. Розв’яжіть рівняння:
варіанти відповіді: 1)15; 2) 17; 3) 12; 4) 4.
№2. Розв’яжіть рівняння:
і вкажіть найменший корінь рівняння
Варіанти відповіді: 1) 6; 2) 5; 3) -5; 4)-6;
Самостійна робота
Варіант №2.
№1. Розв’яжіть рівняння:
Варіанти відповіді: 1) 4; 2) 3; 3) -1; 4) 9;
№2. Розв’яжіть рівняння:
Варіанти відповіді: 1) 26; 2) -3; 3)-1; 4) 0.
|
13. |
Контрольна робота№1. |
16.10.2019 |
1 |
|
|
14. |
Аналіз контрольної роботи. Означення та властивості степеня з раціональним показником. |
18.10.2019 |
1 |
|
|
15. |
Степеневі функції, їхні властивості та графіки. |
23.10.2019 |
1 |
|
|
16. |
Ірраціональні рівняння. |
25.10.2019 |
1 |
|
|
17. |
Розв’язування ірраціональних рівнянь. |
06.11.2019 |
1 |
|
|
18. |
Розв’язування вправ. |
08.11.2019 |
1 |
|
|
19. |
Розв’язування вправ. Самостійна робота. |
13.11.2019 |
1 |
|
|
20. |
Підготовка до контрольної роботи. |
15.11.2019 |
1 |
|
|
21. |
Контрольна робота№2.
|
20.11.2019 |
1 |
|
|
|
Тема №2. Тригонометричні функції числового аргументу. Формули додавання та наслідки з них. |
|
|
|
|
22. |
Аналіз контрольної роботи. Синус, косинус, тангенс, котангенс кута. Радіанна міра кутів. |
22.11.2019 |
1 |
|
|
23. |
Розв’язування вправ. |
27.11.2019 |
1 |
|
|
24. |
Тригонометричні функції числового аргументу. |
29.11.2019 |
1 |
|
|
25. |
Основні співвідношення між тригонометричними функціями одного аргумента. |
04.12.2019 |
1 |
|
|
26. |
Знаки значень тригонометричних функцій. Парність і непарність тригонометричних функцій. |
06.12.2019 |
1 |
|
|
27. |
Формули зведення. |
11.12.2019 |
1 |
|
|
28. |
Формули додавання для тригонометричних функцій та наслідки з них. |
13.12.2019 |
1 |
|
|
13. |
Контрольна робота№1. |
15.10.2019 |
1 |
|
|
14. |
Аналіз контрольної роботи. Означення та властивості степеня з раціональним показником. |
16.10.2019 |
1 |
|
|
15. |
Степеневі функції, їхні властивості та графіки. |
21.10.2019 |
1 |
|
|
16. |
Ірраціональні рівняння. |
23.10.2019 |
1 |
|
|
17. |
Розв’язування ірраціональних рівнянь. |
04.11.2019 |
1 |
|
|
18. |
Розв’язування вправ. |
06.11.2019 |
1 |
|
|
19. |
Розв’язування вправ. Самостійна робота. |
11.11.2019 |
1 |
|
|
20. |
Підготовка до контрольної роботи. |
13.11.2019 |
1 |
|
|
21. |
Контрольна робота№2.
|
18.11.2019 |
1 |
|
|
|
Тема №2. Тригонометричні функції числового аргументу. Формули додавання та наслідки з них. (11год) |
|
|
|
|
22. |
Аналіз контрольної роботи. Синус, косинус, тангенс, котангенс кута. Радіанна міра кутів. |
20.11.2019 |
1 |
|
|
23. |
Розв’язування вправ. |
25.11.2019 |
1 |
|
|
24. |
Тригонометричні функції числового аргументу. |
27.11.2019 |
1 |
|
|
25. |
Основні співвідношення між тригонометричними функціями одного аргумента. |
02.12.2019 |
1 |
|
|
26. |
Знаки значень тригонометричних функцій. Парність і непарність тригонометричних функцій. |
04.12.2019 |
1 |
|
|
27. |
Формули зведення. |
09.12.2019 |
1 |
|
|
28. |
Формули додавання для тригонометричних функцій та наслідки з них. |
11.12.2019 |
1 |
|
Тема уроку:
Розв’язування ірраціональних рівнянь.
Підготувала вчитель математики:
Федоришин Н.Д. (10 клас)
листопад 2019 р
про публікацію авторської розробки
Додати розробку