Тема: Розв’язування прямокутних трикутників
1
Тема: Розв’язування прямокутних трикутників
Мета уроку: вдосконалити вміння учнів знаходити значення синуса, косинуса і тангенса кута та застосовувати їх для розв'язування прямокутних трикутників; розвивати в учнів логічне мислення, уяву, вміння висувати гіпотези та аналізувати; виховувати в учнів самостійність, спостережливість, наполегливість та увагу.
Тип уроку: урок застосування знань, умінь та навичок.
Обладнання: підручник Єршова А. П. Геометрія: Підручник для 8 кл. Загальноосвітніх навчальних закладів /А. П. Єршова, В. В. Голобородько, О. Ф. Крижановський, С. В. Єршов. – Х.: «Ранок», 2016., «математичні дерева», картки.
Епіграф уроку:
Світ, що нас оточує, - це світ геометрії.
Тож давайте його пізнавати!
Піфагор
Хід уроку:
- Організаційний момент.
- Перевірка домашнього завдання.
Гра «Правда – неправда». Один учень відповідає, а інші звіряються. Після цієї гри вчитель дає відповіді на запитання, що виникли в учнів.
- Оголошення теми і мети уроку.
- Актуалізація опорних знань.
Сьогодні ми подорожуємо до «країни трикутників». Але перш ніж потрапити в цю країну, нам потрібно пройти митний контроль, відповівши на кілька запитань митників.
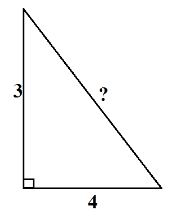
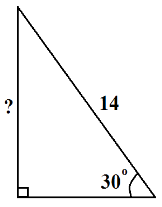
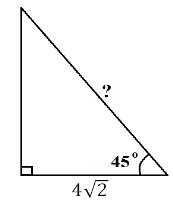
Очікуванна відповідь: 5, 7, 8.
Молодці. Митницю ви пройшли, сіли в літак і прилетіли в «країну трикутників». І тут перед вами відкрилася галявина «Теоретична». Жителі цієї країни пропонують вам пограти у математичний футбол. Тож приймемо їхню пропозицію. Правила гри такі: якщо ви відповідаєте правильно, то гол у ворота жителів галявини, якщо неправильно, то гол у ваші ворота.
Продовжте речення:
- Синус кута дорівнює відношенню протилежного катета до... (гіпотенузи);
-
cos 30o = …(
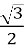 );
);
- Сума квадратів катетів дорівнює… (квадрату гіпотенузи);
- Прилеглий катет дорівнює добутку гіпотенузи на… (косинус кута);
- Тангенс кута дорівнює відношенню протилежного катета до… (прилеглого);
-
sin 45o = … (
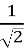 );
);
- гіпотенуза дорівнює відношенню протилежного катета до…(косинуса кута);
-
tg 60o = …(
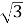 );
);
Матч закінчився з рахунком… Перемогли….
- Розв’язування задач.
Відвідавши галявину «Теоретичну» і позмагавшись з її жителями, ви з ними потоваришували, і вони вам порадили відвідати узлісся «Практичне». Ви, не задумуючись, попрямували туди. І тут перед вами відкрився краєвид з дерев «країни трикутників». Давайте відпочинемо під кроною лісу.
(Учень виходить до дошки, обирає одне з трьох «математичних дерев», які прикріплені магнітами до магнітної дошки, з іншого боку якого знаходиться одна із трьох задач, і розв’язує цю задачу.)
Задача №1.
Кут при вершині рівнобедреного трикутника дорівнює ![]() , висота, проведена до бічної сторони, дорівнює h. Знайдіть основу трикутника.
, висота, проведена до бічної сторони, дорівнює h. Знайдіть основу трикутника.
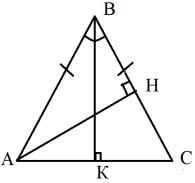
Дано: ∆АВС (АВ = ВС), кут В = ![]() , АН = h. Знайти:.АС.
, АН = h. Знайти:.АС.
Розв’язання:
1).З ∆ АВН (кут Н = 90о): sin ![]() =
= ![]() AB =
AB =![]() ;
;
2) BK – висота, бісектриса, медіана. Кут АВК = ![]() ;
;
3) sin ![]() =
= ![]()
![]() AK = AB
AK = AB![]() sin
sin ![]() =
= 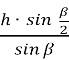 ;
;
4) AC = 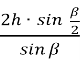 .
.
Відповідь: основа трикутника дорівнює 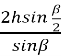 .
.
Задача №2.
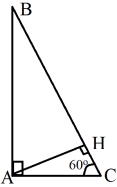 Висота, проведена з вершини прямого кута трикутника, дорівнює 6
Висота, проведена з вершини прямого кута трикутника, дорівнює 6![]() , гострий кут дорівнює 60о. Знайдіть сторони трикутника.
, гострий кут дорівнює 60о. Знайдіть сторони трикутника.
Дано: ∆АВС (кут А = 90 о), АН = 6![]() см, кут С = 60о.
см, кут С = 60о.
Знайти:.АВ,.АС,.ВС.
Розв’язання:
1).sin.60.o.=.![]() AC
AC![]() =.
=.![]() .12.(см);
.12.(см);
2) tg 60o = ![]() AB = AC
AB = AC![]() tg 60o = 12
tg 60o = 12![]() (см);
(см);
3) кут В = 30о ![]() ВС = 2АС = 24 (см).
ВС = 2АС = 24 (см).
Відповідь: сторони трикутника дорівнюють 12![]() см, 12 см, 24 см.
см, 12 см, 24 см.
Задача №3.
Більша діагональ ромба дорівнює 4![]() , а гострий кут – 60о. Знайдіть сторону та меншу діагональ ромба.
, а гострий кут – 60о. Знайдіть сторону та меншу діагональ ромба.
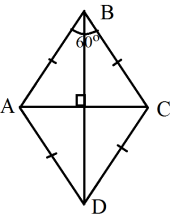 Дано: АВСD – ромб, ВD = 4
Дано: АВСD – ромб, ВD = 4![]() см, кут В = 60о.
см, кут В = 60о.
Знайти: АВ, АС.
Розв’язання:
-
ВО =
 ВD = 2
ВD = 2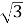 (см);
(см);
-
ВО – висота, бісектриса, медіана
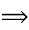 кут АВО =30о
кут АВО =30о
-
AO = BO
 tg 30o = 2
tg 30o = 2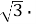
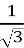 = 2 (cм);
= 2 (cм);
- АС = 4 (см);
-
Кут АВО = 30о
 АВ = 2
АВ = 2  АО = 4 (см).
АО = 4 (см).
Відповідь: сторона ромба дорівнює 4см, діагональ ромба – 4 см.
- Підсумки уроку.
Ви побували в цікавих місцях, але час повертатися додому. Ваші друзі з «теоретичної» галявини підказали, що є чарівний пень в цьому узліссі, який може повернути вас додому. Пень взамін повернення попросив виконати деяке його доручення:
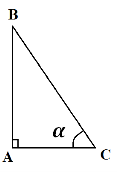 Відновити правильність записів на його корі (на дошці):
Відновити правильність записів на його корі (на дошці):
-
tg
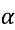 =
= 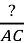 ;
;
-
BC =
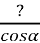 ;
;
-
AB = BC
 ?
?
Очікувана відповідь: АВ, АС, sin ![]() .
.
- Домашнє завдання.
- Повторити п. 19-21
- Розв’язати задачі до підготовки контрольної роботи №5 с.225


про публікацію авторської розробки
Додати розробку
