ЦИКЛ УРОКІВ ІЗ  АЛГЕБРИ  У 10 КЛАСІ З ТЕМИ «ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ»
З ВИКОРИСТАННЯМ ІНТЕРАКТИВНИХ МЕТОДІВ І ПРИЙОМІВ

 

УРОК 33

Тема уроку: радіанне  вимірювання  кутів і дуг.

Мета уроку: узагальнити і систематизувати  знання учнів

про радіанну міру вимірювання кутів і дуг. Формувати  уміння визначати радіанну міру кута за градусами і навпаки. Розвивати пізнавальний інтерес, культуру математичної мови.

Хід уроку

І. Організаційний момент.

ІІ. Актуалізація опорних знань учнів.        

Мозковий штурм

1) Кутом якої чверті є кут 370°?

2) Запишіть всі кути повороту, кінцевий радіус яких знахо­диться на додатній півосі ΟΥ?

3) Обчисліть: 2cos 60° + 2sin 30°. Знайдіть cos 720°, sin (-270°).

4) Який знак має tg (-50°).  Відповідь: 1) І; 2) 90° + 360°n, n Ζ; 3) 2;  1;  1; 4) -.

IІI. Сприймання і усвідомлення нового матеріалу.

Як відомо, кути вимірюються в градусах, хвилинах, секундах,

Градусом називається частина розгорнутого кута.

Таким чином, розгорнутий кут дорівнює 180°, прямий кут дорівнює 90°.

Між градусами, хвилинами і секундами існують співвідно­шення: 1º = 60', 1' = 60'', 1' = , 1' = . Крім градусної міри, використовуються і інші одиниці вимі­рювання кутів. У математиці і фізиці це радіанна міра кута.

1 радіан — центральний кут, який опирається на дугу, довжина якої дорівнює радіусу (рис. 41).

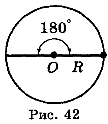
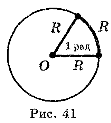Установимо зв’язок між радіанним і градусним вимірюванням кутів. Куту, що дорівнює 180°, відповідає півколо, тобто дуга, довжина якої дорівнює πR (рис. 42). Щоб знайти радіанну міру кута в 180°, треба довжину дуги π-R розділити на

довжину радіуса R: . Отже, радіанна міра кута в 180° дорівнює π:180° = π рад

 

Із цієї формули одержуємо (розділивши ліву і праву частини рівності на 180):

1° = рад, або 1° 0,017 рад.

Із рівності 180° = π рад також одержуємо (розділивши ліву і праву частини рівності на π):

1 рад = , або 1 рад 57°.

Розглянемо приклади переходу від радіанної міри до градус­ної і навпаки.   

Приклад 1. Виразіть в радіанах величини кутів 30°; 45°; 60°; 90°.

Розділимо ліву і праву частини рівності 180° = π рад послідовно  на 6, 4, 3, 2, одержимо 30° = рад, 45° = , 60° = ; 90° = рад.

Приклад 2. Виразіть в градусах величини кутів рад, рад, рад, рад.  

Розділимо ліву і праву частини рівності 180° = π рад послідовно на 10; 5; 12; 18, одержимо рад = 18º;=36º;=15º; рад = 10º.

Приклад 3. Знайдіть в градусах 3,5 рад. Через те що 1 рад = , 3,5 рад  = 3,5 ·   = = 201° .

Приклад 4. Знайдіть радіанну міру кута в 72°.Через те що 1° =рад, 72° = 72 · рад = рад 1,3 рад.

Радіанна міра кута зручна для обчислення довжини дуги кола. Через те що кут в 1 радіан стягує дугу, довжина якої дорівнює R, то кут в α радіан стягує дугу довжиною: l = αR.

Якщо радіус кола дорівнює одиниці, то l = α, тобто довжина дуги дорівнює величині центрального кута, що опирається на цю дугу в радіанах.

IV. Формування умінь визначати радіанну міру кута за градусною і навпаки.

Виконання вправ     Робота в групах

1. Запишіть у радіанній мірі кути: а) 120°, б) 300°; в) -405°, г) -22,5°. Відповідь: а) ;б) ;    в) ;  г)

2. Подайте в градусній мірі кути: а) ; б) 2,5π; в) 0,3π; г) .Відповідь: а) 135°; б) 450°; в) 54°; г) 660°.

3. Подайте в радіанній мірі кути (скористуйтеся таблицями або калькулятором):

а) 20° 12';    б) 54° 23';    в) 136° 27';    г) 127° 15'.

Відповідь: а) 0,3586;   6)0,9492;  в) 2,3815;  г) 2,221.

4. Подайте в градусній мірі кути (скористайтеся таблицями або калькулятором):

а) 15;        б) 2;          в) 1,1417;     г) 4,3982.

Відповідь: а) 859,87°;   б) 114,65°;   в) 65° 25';   г) 252°.

V. Підведення підсумків уроку.

VІ. Домашнє завдання:  §4, вивчити п.18,  №488, №489, №496.

 

УРОК  34

Тема уроку: тригонометричні функції кута: синус, косинус, тангенс, котангенс.

Мета уроку: повторити означення тригонометричних функцій го­строго кута прямокутного трикутника і ввести озна­чення тригонометричної функції довільного кута, розвивати стійку увагу, чіткість і послідовність у викладенні думок, виховувати уважність.

 

Хід уроку

І. Організаційний момент.

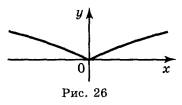
ІІ. Актуалізація опорних знань учнів. Побудуйте графіки функцій (індивідуальні картки):

а) ; б) ; в) ; г) , д) ;  е)

 

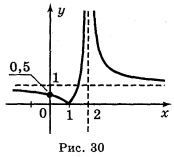
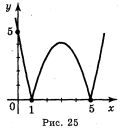
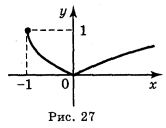
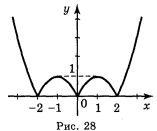
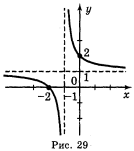
Відповідь: а) рис. 25; б) рис. 26; в) рис. 27; г) рис. 28, д) рис. 29;е) рис. 30.

 

 

IІI.

 

 

 

 

 

 

 

Повторення відомостей про тригонометричні функції гострих кутів прямокутного трикутника.

 

Мікрофон

1. Дайте означення синуса гострого кута прямокутного трикут­ника.

2. Дайте означення косинуса гострого кута прямокутного три­кутника.

3. Дайте означення тангенса гострого кута прямокутного трикутника.

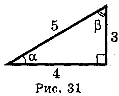
4. Користуючись рис. 31, знайдіть sin α, cos α, tg α, ctg α, sin β, cos β, tg β, ctg β.

5. Обчисліть:       чи справді це так?

а) 2 cos 60° + cos 30°;   б) 3tg45°·tg60° ;

в) 2 cos 30° + 6 cos 60° – 4 tg 45°; г) 2 ctg 60° – 2 sin 60° .

6. Спростіть:   a) (l – cosα)(l + cosα);        6) tgα – ctgα + sin² α + cos² α.

IV. Повторення відомостей про тригонометричні функції довільного кута.

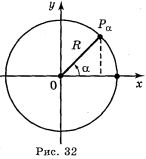
У курсі геометрії для кутів від 0° до 180° було дано означення синуса, косинуса, тангенса за допомогою кола.  (рис. 32). Синусом кута називається відношення ординати точки Р_α(х; у) кола до його раді­уса: , , ,.

V.Розв’язування вправ. Побудуйте коло з центром у початку координат і кути пово­роту, що дорівнюють:

а) 90° + 360° n, (п Z);      б) 180° + 360° n, (п Z). Вирішення проблеми

Визначте, кутом якої чверті є кут α, якщо кут а дорівнює: а) 181°;   б) 179°;

в) 271°;   г) 361°;   д) 345°;   є) 800°.

IV. Підсумок уроку.

V. Домашнє завдання: §4, вивчити п.19, повторити п.18, №513, №519, №523.

 

УРОК  35

Тема уроку: тригонометричні функції числового аргументу.

Мета уроку: формування поняття тригонометричних функцій чис­лового аргументу; вивчення значень тригонометрич­них функцій деяких чисел (кутів), зміни знаків три­гонометричних функцій у координатних чвертях, розвивати логічне мислення.

Хід уроку

І. Організаційний момент.

ІІ. Перевірка домашнього завдання.  Розв'язування вправ аналогічних до домашніх.

1. Подайте в радіанній мірі кути:

а) 5°;    б) 1140º;      в) -765°;      г) 67° 5'.  Відповідь: а) ;      б) π;    в) π; г)  .

2. Подайте в градусній мірі кути: а) , б) 1,25π; в) 1; г) 10.Відповідь: а) 105°;  б) 225°;  в) 57,32°;

  г) 573,25°.

3. Знайдіть довжину  дуги, якщо на неї опирається центральний  кут α = , а радіус кола дорівнює 10 м.

 Відповідь: 9π м.

ІII. Сприймання і усвідомлення понять синуса, косинуса, тангенса і котангенса числа.

Розглянемо на координатній площині коло радіуса 1 з центром у початку коорди­нат, яке називається одиничним

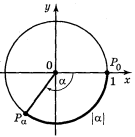
1) Якщо α > 0, то, рухаючись по колу із точки Р_о в напрямі проти годинникової стрілки, опишемо по колу шлях довжи­ною а, кінцева точка цього шляху і буде шуканою точкою Ρ_α.

2) Якщо α < 0, то, рухаючись із точки Ρ_о (рис.) в напрямі за годинниковою стрілкою, опишемо по колу шлях дов­жиною |α|; кінець цього шляху і буде шукана точка Р_α.  3) Якщо α = 0, то поставимо у відповідність точку Р_о.

Якщо α = α_о + 2πk, де k — ціле число, то при повороті на кут α одержуємо одну і ту саму точку, що й при повороті на кут α_о.

Виконання вправ

1. Яким числам відповідають точки Р₀, Р, М, K, L, S (рис. 45), якщо відомо, що Ν — середина дуги Р₀К, а дуги Р₀Р, РМ, МК — рівні.

Відповідь: 2πn; +2πn;+2πn; + 2πn; + 2πn; π + 2πn; - + 2πn, n Z.  2. Позначте на одиночному колі точки, які відповідають числам:

а) + 2πn , - +2πn, + 2πn, -+ 2πn, де n Ζ;б) + 2πn ,+ 2πn ,+ 2πn+ 2πn,

    - + 2πn,n Ζ.

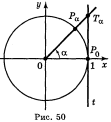
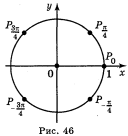
Відповідь: а) рис. 46 (кожна чверть кола поділена на 2 рівні частини);

б) рис. 47 (кожна чверть кола поділена на 3 рівні частини).

3.

Позначте на одиночному колі точки, які відповідають числам 1; 2; 3;-5. Відповідь: рис. 48.

 

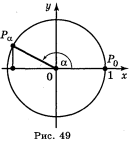
Синусом числа α називається ордината точки Р_α, утвореної пово­ротом точки Р_α (1; 0) навколо початку координат на кут в α раді­ан (позначається sin α) (рис. 49).Синус визначений для будь-якого числа α.

Косинусом числа α називається абсциса точки Р_α, утвореної по­воротом точки Р_α (1; 0) навколо початку координат на кут в α радіан (позначається cos α) (рис. 49).Косинус визначений для будь-якого числа α.

Виконання вправ    Мозковий штурм

1. Обчисліть:a) cos 7π;     б) sin 7π;     в) cos;     r) sin . Відповідь: а) -1;   б) 0;   в) 0;    г) 1.

2. Обчисліть:

a) ; б) ; в) sin π + sin 1,5π. Відповідь: а) 0; б) -1; в) -1;      

Тангенсом числа α називається відношення синуса числа α до його косинуса:   ; у = tgα.

Тангенс визначений для всіх а, крім тих значень, для яких cos α = 0, тобто, α = + πn, n Ζ.

Виконання вправ Обчисліть:  а) tg π;  б) tg (-π);  в) tg 4π;  r) tg . В. а) 0;   б) 0;   в) 0;  г) не визначений.

2. Визначте знак числа:  а) tg ; б) tg ; в) tg ; г) ctg .

Відповідь: а) мінус; б) плюс; в) мінус; г) мінус.

IV. Визначення значень тригонометричних функцій деяких чисел.

Через те що поворот на кут в α радіан співпадає з поворотом 180 на кут —α градусів, аргумент синуса і косинуса можна виразити як в градусах, так і в радіанах. Наприклад, при повороті точки (1; 0) на кут , тобто на кут 90º, тому sin = sin 90° = 1, cos = cos 90° = Ο .

 

α	0					π		2π
	0°	30°	45°	60°	90°	180°	270°	360°
sin α	0				1	0	-1	0
cos α	1				0	-1	0	1
tg α	0		1		не існ.	0	не існ.	0
ctg α	не існ.		1		0	не існ.	0	не існ.

Виконання вправ. Обчисліть: а) 3sin + 2cos – tg ; б) 5sin +3tg – 5cos – 10ctg ;В а) ; б)-7;  

V. Вивчення зміни знаків тригонометричних функцій.

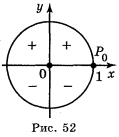
Число sin α — це ордината відповідної точки Р_α, тому sin α > О, якщо точка розташована вище осі абсцис, тобто в І і II чвертях (рис. 52). Якщо ця точка лежить нижче осі абсцис, то її ордината від'ємна в третій і четвертій чвертях.

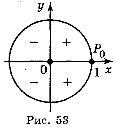
Число cos α — це абсциса точки Р_α, тому cos α > 0 в І та IV чвертях, cos α < 0 в II та III чвертях (рис. 53).

 

    

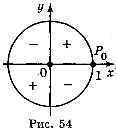
Так як , , то tg α > 0 і ctg α > 0, якщо sin α і cos α мають однакові знаки, тобто в І і III чвертях, і tg α < 0 і ctg α < 0 в II і IV чвертях (рис. 54).

Виконання вправ                            Синтез думок

1. У якій чверті знаходиться точка Ρ_α , якщо:

а) sin α > 0 і cos α > 0;     б) sin α > 0 і cos α < 0;    в) sin α < 0 і cos α > 0;     r) sin α < 0 і cos α < О?

Відповідь: а) І;         б) II;        в) IV;       г) III.

 

2. Якій чверті належить Р_α, якщо:

а) sin α cos α > 0;           б) sin α cos α < 0;     в) tg α cos α > 0;            г) ctg α sin α < 0?

Відповідь: а) І або III; 6) II або IV; в) І або II; г) II або III.

3. Знайдіть знак виразу:

а) cos ; б) sin ; в) ctg (π + α);   г) tg , якщо 0 < α < .

Відповідь: а) мінус;    б) плюс;    в) плюс;    г) плюс.

4. Визначте знак виразу:

а) sin105° – cos105°; б) cos155° – sin255°; в) tg127° · ctg200°; г) tg351° · ctg220°.

Відповідь: а) мінус;    б) плюс;    в) мінус;   г) мінус.

5. Визначте знак добутку:

а) tg 2 · tg 3 · ctg 3 · cos 1;  б) sin 1 · cos 2 · tg 3 · ctg 4.

Відповідь: а) мінус;    б) плюс.

VІ. Підсумок уроку.

VІI. Домашнє завдання: §4, вивчити п.19 (ІІ част.), п.20 (Ічаст.), №539, №543, №553.

 

УРОК №36

Тема: синус, косинус, тангенс, котангенс кута. Тригонометричнi функцiї числового аргумента.       Розв’язування вправ.  Самостійна робота.

Мета: закріпити  поняття синуса, косинуса, тангенса, котангенса кута, тригонометрични  функцiй числового аргумента; домогтися засвоєння учнями значень тригонометричних функцiй окремих чисел та знакiв синуса, косинуса, тангенса i котангенса в кожнiй iз координатних чвертей, удосконалювати вміння розв’язувати вправи, розвивати стійкі обчислювальні навички.

Хiд уроку

І. Органiзацiйний етап

ІІ. Перевiрка домашнього завдання. Самостійна робота.

Вставте замiсть крапок пропущенi слова в речення.      Незакінчене речення 

                              Варіант 1 (2)

1. Якщо , то кут є кутом… чвертi.

2. Якщо , то кут є кутом… чвертi.

3. Якщо , то кут є кутом… чверті.

4. Якщо , то кут є кутом… чвертi.

5. Якщо градусна  мiра кута дорівнює 60° [90°],то його радіанна мiра дорівнює ...

6. Якщо  градусна  мiра кута дорівнює 270° [45°],то його радіанна  мiра дорівнює …

7. Якщо радiанна мiра кута дорiвнює , то його градусна  мiра дорiвнює…

8. Якщо радіанна міра кута дорівнює , то його градусна міра дорівнює …

9. Якщо радiанна  мiра кута дорiвнює , то його градусна мiра дорівнює …

ІІІ. Формулювання мети i завдань уроку

  Закріпити поняття тригонометричних функцій числового аргумента, виробити вміннч й навички їх застосування при розв’язуванні вправ.

ІV. Актуалiзацiя опорних знань Фронтальне опитування   Мозковий штурм

1. Сформулюйте означення: синуса гострого кута прямокутного трикутника; косинуса гострого кута прямокутного трикутника; тангенса гострого кута прямокутного трикутника, синуса, косинуса, тангенса, котангенса числового аргумента, перевірити знання таблички.

2. Сформулюйте означення тригонометричних функцiй для кутiв від до.

V. Формування вмінь      Виконання  вправ    Коло ідей

1. Синус якого числа на вiдрiзку дорiвнює:  а) 0; б) 1; в) ; г) ?

2. Косинус якого кута вiдрiзка дорiвнює:  а) 0; б) 1; в) ; г) ?

3. Укажiть декiлька значень , при яких: а) ; б) ; в) ; г) ; д) ; е) не існує.

4. Який знак має: а) ; б) ; в) ; г) ; д) ; е) ; ж) ;

5. Знайдiть значення виразу:

а) ;

б) ;

VІ. Пiдсумки уроку      Контрольнi запитання

1. Сформулюйте означення синуса, косинуса, тангенса та котангенса кута; тригонометричних функцiй числового аргумента.

2. Укажiть область визначення та множину значень функцій , , , .

3. Для кутiв якої чв.коорд. площини:

а) i мають однаковi знаки; б) і мають рiзнi знаки;

VІІ. Домашнє завдання: §4, повторити п.п.19, 20, №549, №555.

 

УРОК  37

Тема уроку: співвідношення між тригонометричними функціями одного аргументу.

Мета уроку: вивчення співвідношення між тригонометричними функціями одного аргументу, формування умінь за­стосовувати вивчені співвідношення для тотожних перетворень виразів, розвивати логічне мислення.

Хід уроку

І. Організаційний момент.

II. Мотивація навчання.

Дуже часто при розв'язуванні задач виникає проблема: зна­йти значення тригонометричних функцій, якщо задано лише зна­чення однієї з них. Отже, на сьогоднішньому уроці ми повинні згадати формули (залежності), які пов'язують тригонометричні функції одного і того самого аргументу.

III. Сприймання і усвідомлення нового матеріалу.

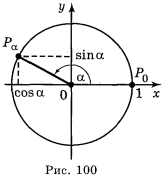1. Співвідношення між синусом і косинусом:

 

cos² α + sin² α = 1. Ця рівність називається осн. тригонометричною тотожністю.

З основної тригонометричної тотожності можна виразити sin α через cos α і навпаки.                            , .

 Виконання вправ         Розумовий  штурм

1. Знайдіть cos α, якщо sin α = 0,6 і  < α < π.    Відповідь: cos α = -0,8.

2. Спростіть вирази:

а) 1 + sin² α + cos² α;  б) 1 – sin² α – cos² α; в) 2sin² α + cos² α – 1;  г) (1 – cos α)(l + cos α);     

д) ;                  є) sin⁴ α – cos⁴ α  + 1.      

 Відповідь: а) 2; 6) 0; в) sin² α; r) sin² α; д) tg²α; є) 2sin²α.

 

3. Доведіть тотожності:    а) (1 – cos 2α)(l + cos 2α) = sin² 2α;    6) cos⁴ α – sin⁴ α = cos² α – sin² α;

в) (sin² α – cos² α)² + 2cos²α sin²α = sin⁴ α + cos⁴ α;

r) 2cos²α sin²α + cos⁴α + sin⁴α = 1;    д) sin⁶ α + cos⁶ α = 1 – 3sin²α cos²α;

2. Співвідношення між тангенсом і котангенсом. Згідно з визначенням тангенса і котангенса,

,  , , ;

 

Виконання вправ              Робота в парах

1. Знайдіть   а) tg α, якщо ctg α = ;     б) ctg α, якщо tg α = -1;  в) tg α, якщо ctg α = 0.

Відповідь: а) ;      б) -1;       в) не існує.

2. Дано: х = 2tg α, у = ctg α. Знайдіть ху.   Відповідь: ху = .

3. Дано tg α + сtg α = 2. Знайдіть tg ² α + сtg² α.   Відповідь: 2.

 

4. Спростіть:  а) tg α · сtg α – 1; б) sin² α – tg α · сtg α; в) tg 1° · tg 3° · tg 5° · ... · tg 89°.  В. а) 0;   б) – соs α;   в) 1.

6. Доведіть тотожності:     а) (tg α + сtg α)² - (tg α - сtg α)² = 4; б) 4 + (сtg α - tg α)² = (сtg α + tg α)²,

                в) ;   г) ;   

3. Співвідношення між тангенсом і косинусом, котангенсом і си­нусом.

звідси:  , де ,        , де .

IV. Підведення підсумків уроку.

V. Домашнє завдання:§4, вивчити п. 24, №617, №623, №626.

 

УРОК 38

Тема:  основнi спiввiдношення мiж тригонометричними функцiями одного аргументу.  Самостійна робота.

Мета: домогтися засвоєння учнями основних спiввiдношень мiж тригонометричними функцiями одного аргумента, розвивати стійку увагу, навички самоконтролю.

Хiд уроку

І. Органiзацiйний етап

ІІ. Перевiрка домашнього завдання

Засвоєння матерiалу попереднього уроку  перевiряю за допомогою самостiйної роботи з подальшою перевiркою  (взаємоперевiркою за готовими відповідями).

Самостiйна робота        Варiант 1

 1. Знайдiть значення виразу: а);б).

2. Обчислiть: , якщо .

 3. Визначте знак виразу .

4. Вiдомо, що . Порiвняйте з нулем значення виразу:  а) ; б) .

                                          Варiант 2   

  1. Знайдiть значення виразу:

а) ;   б) .

2. Обчислiть: , якщо .

 3. Визначте знак виразу .

4. Вiдомо, що . Порiвняйте з нулем значення виразу:   а) ; б) .

ІІІ. Формулювання мети i завдань уроку   

Вивчення спiввiдношень мiж тригонометричними функцiями одного аргумента i є завданням цього уроку.

ІV. Актуалiзацiя опорних знань i вмінь.

Повторити формули, вивчені на попередньому уроці.  Мікрофон

V. Засвоєння знань,  формування вмінь       Мозковий штурм

1. Виразiть: а)через ; б) через ; в) через і ; г) через і .

2. Знайдiть значення виразу:   а) ; б) .

3. Вiдомо, що . Знайдiть значення виразу .

4. Обчислiть значення виразу , якщо вiдомо, що .

5. Порiвняйте: а) і 0,4; б) і 1,2.

6. Вiдомо, що . Знайдiть:  а) , якщо ; б) , якщо .

5. Обчислiть , якщо вiдомо, що і . Яких значень може набувати число a?

VІ. Пiдсумки уроку Чи iснує значення кута таке, для якого:а) , а

VІІ. Домашнє завдання: §4, повторити п.24, №627, №629, №631.

 

УРОК 39

Тема уроку: формули зведення.

Мета уроку: вивчення формул зведення, формування умінь учнів  застосовувати вивчені формули для спрощення ви­разів та обчислень, розвивати стійкі обчислювальні навички, чіткість і послідовність у викладенні думок.

Хід уроку

І. Перевірка домашнього завдання.

1. Відповіді на питання учнів, що виникли в процесі виконан­ня домашнього завдання.     

 2. Самостійна робота.  

Варіант 1

1. Спростіть  . (3 бали)                   2. Знайдіть tg 2α, якщо tg α = - 0,4. (3 бали)

3. Спростіть . (3 бали)     4. Обчисліть . (З бали)

 

Варіант 2

1. Спростіть  . (З бали)              2. Знайдіть tg 2β, якщо tg β = 6. (З бали)

3. Спростіть . (З бали)     4. Обчисліть . (З бали)

Відповідь: В-1. 1. –tgα tgβ .   2..   3. 0.   4. .             В-2. 1. –сtgα tgβ.  2.  .  3. 0.  4. .

 

II. Сприймання і усвідомлення формул зведення.

Тригонометричні функції чисел виду ± α, π ± α; ± α, 2π ± α можуть бути виражені через функції кута α за допомогою формул, які називаються формулами зведення.

 

,   ,  ,, ,  .

 

,   ,  , ,   ,  .

,   ,  ,  .

 

1) В правій частині формули ставиться той знак, який має ліва частина при умові 0 < α < .

2) Якщо в лівій частині формули кут дорівнює ± α, ± α, то  синус замінюється на косинус, тангенс — на котангенс і на­впаки. Якщо кут дорівнює π ± α, то заміна не виконується.

Виконання вправ              Робота в парах

1. Приведіть до тригонометричних функцій числа а:

а); б);  в) сtg (π – α); г) tg (π + α); д) sіn (π + α); є).

Відповідь: а) соs α; б) - sіn α; в) - ctgα; г) tg α; д) - sіn α; є) сtg α.

 

2. Знайдіть:а) sіn ;     б) соs ;     в) tg ;      г) sіn . В: а) ;  б) - ;  в) - ;   г) .

3. Спростіть:  а) 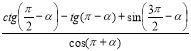; б) .  

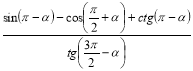Відповідь: а) 1. б) –1.

III. Підведення підсумків уроку. Повторити правила для формул зведення.

IV. Домашнє завдання: §4, вивчити п.26, повторити п.24, № 677, №679, №681 (1; 3).

 

УРОК 40

Тема: Розв’язування вправ.

Мета: удосконалити знання учнiв основних спiввiдношень мiж тригонометричними функцiями одного аргумента; формул зведення, розвивати логічне мислення.

Хiд уроку

І. Органiзацiйний етап

ІІ. Перевiрка домашнього завдання

1) Ретельно перевіряється  правильність  виконання вправ домашньої роботи в учнiв,  якi потребують додаткової педагогiчної уваги.

2)     Знайди помилку        1. Якщо і , то .

2. Якщо і , то .             3. Якщо , то .

ІІІ. Формулювання мети та завдань уроку.  Мотивацiя навчальної дiяльностi

Для того щоб створити вiдповiдну мотивацiю навчальної дiяльностi, пропоную  учням завдання.

Завдання. Знайдiть значення виразу , якщо .

Отже, завдання уроку — навчитися застосовувати спiввiдношення  мiж тригонометричними функцiями одного аргумента до перетворення виразiв,  виробити вміння і навички при їх перетворенні.

ІV. Актуалiзацiя опорних знань                      Математичний диктант    взаємоперевірка

1. Виконайте дiї: а) ; б) . 2. Подайте у виглядi квадрата: а) ; б) .

3. Спростiть вираз: а) ; б) ; в) . 4. Виконайте дiї: .

V. Застосування знань             Мозковий штурм

  Приклад 1. Спростiть вираз .

Розв’язання. Скориставшись формулами і ,

дістанемо: .

Приклад 2. Спростiть вираз .          

Розв’язання. Маємо:

.

VІ. Формування вмінь

1. Спростіть вираз:  а) ; б) ;  в) ; г) ;

д) ; е) .

2.  Обчислiть: а) , якщо ; б) , якщо .

VІІ. Пiдсумки уроку      Спростiть вираз: а) ; б) ; в) ; г) ;

VІІІ. Домашнє завдання: §4, повторити п.18, п.19, п.20, п24, п.26, №683, №681(2, 5).

 

УРОК 41

Тема: розв’язування вправ. Самостійна робота.

Мета: домогтися засвоєння учнями таких властивостей тригонометричних функцiй, як перiодичнiсть, парнiсть, непарнiсть, виробити вміння й навички при тотожному перетворенні виразів, розвивати навички самоконтролю.

Хiд уроку

І. Органiзацiйний етап

ІІ. Перевiрка домашнього завдання

Зiбрати зошити учнiв iз виконаною домашньою роботою.

ІІІ. Формулювання мети i завдань уроку

Узагальнити й систематизувати знання учнів із теми, підготуватися до написання контрольної роботи.

ІV. Актуалiзацiя опорних знань     Взаємне навчання

1. Яка функцiя називається парною? непарною?

2. Вiдомо, що функцiя парна.  Знайдiть: , якщо .

3. Вiдомо, що функцiя непарна.  Знайдiть: , якщо

4. Перiодичнiсть  тригонометричних  функцiй. 

5. Парнiсть i непарнiсть тригонометричних функцій         

 6. Повторити основні тригонометричні тотожності.

V. Закріплення вмінь і навичок

1. Обчислiть: а); б) ; в) ; г) ; д) ; е) ; ж) .

2. Знайдiть значення виразу: а) ; б) ; в) ; г) .

 

VІ. Самостійна робота   

Варiант 1                        

1. Спростiть вираз:

а) ; б) ; в) ; г) .

2. Доведiть тотожнiсть:    а) ; б) .

3. Знайдiть значення виразу ,   якщо відомо, що .

4. Доведiть, що при всiх доп. значеннях вираз    набуває одного й того ж значення.

 

Варiант 2                     

1. Спростiть вираз:

а) ; б) ; в) ; г) .

2. Доведiть тотожнiсть:

а) ;

б) .

3. Знайдiть значення виразу , якщо вiдомо, що .

4. Доведiть, що при всiх доп. значеннях вираз    набуває одного й того ж значення.

VІІ. Пiдсумки уроку   Спростiть вираз: ;

VІІІ. Домашнє завдання: §4, повторити п.18-20, п.24, №622, №681(5, 6).

УРОК 42

 

Тема уроку: контрольна робота з теми «Радіанне вимірювання кутів. Основні тригонометричні тотожності».   (№5)

Мета уроку: перевірити знання, уміння і навички учнів з вивче­ної теми, розвивати самостійність, старанність, наполегливість у досягненні мети.

 

Хід уроку

І.  Організаційний момент

ІІ. Контрольна робота

 

Варіант 1

1. Визначити парність (непарність) функції f(x) = х² - cos 2x + tg²х. (2 бали)

2. Знайдіть тригонометричні функції числа . (2 бали)

3. Знайдіть соs α, якщо sіn α = – 0,6 і π < α < . (2 бали)

4. Знайдіть значення виразу 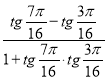. (2 бали )

5. Спростiть вираз:      

 а) ;    б) .

6. Доведiть тотожнiсть:    а) ;    б) .

Варіант 2

 

1. Визначте парність (непарність) функції f(x) = sin x + tg x - х³. (2 бали)

2. Знайдіть тригонометричні функції числа · (2 бали)

3. Знайдіть tg α, якщо соs α = - 0,6 і < α < π. (2 бали)

4. Знайдіть значення виразу sin соs + созsin . (2 бали)

5. Спростiть вираз: а) ;

б) .

6. Доведiть тотожнiсть:

а) ;   

б) .

 

Відповідь: В-1. 1.Парна. 2. ; ; ; .

В-2. 1.Непарна. 2. ; ; ; .

ІІІ. Домашнє завдання. Повторити співвідно­шення між тригоно­метричними функція­ми одного аргументу.

 

УРОК 43

Тема уроку: аналіз контрольної роботи. Періодичність тригонометричних функцій.

Мета уроку: введення поняття періодичної функції; знаходжен­ня найменших додатних періодів тригонометричних функцій; розвивати пізнавальний інтерес, творчі здібності учнів.

Хід уроку

І. Організаційний момент

ІІ. Перевірка домашнього завдання. Аналіз контрольної роботи

Звернути увагу учнів на типові помилки, допущені у контрольній роботі. Виконати подібні вправи, проаналізувати правильність їх розв’язання.

ІII. Формування поняття періодичної функції, період функції.

У природі часто зустрічаються явища, які повторюються пері­одично. Наприклад, Земля при обертанні навколо Сонця періо­дично повертається У своє початкове положення через рік, два роки, три роки і т. д., тому говорять, що період обертання Земля навколо Сонця дорівнює одному року. Періодичний характер мають рухи маховика і колінчатого вала. Властивість періодич­ності мають звукові, електромагнітні явища, робота серця люди­на і т. д. Закономірності періодичних явищ описуються періо­дичними функціями, до вивчення яких ми і приступаємо.

Функція у = f(x) називається періодичною з періодом Т 0, якщо для будь-якого х із області визначення числа х + Т і х – Т також належать області визначення і виконується рівність f(x + Т) =  f(x – Т) = f(x).

Так як одній і тій самій точці Р_α одиночного кола відповідає нескінченна множина дійсних чисел α + 2πk, де k Z, то

sin(α + 2nk) = sin α        cos(α + 2nk) = cos α

Звідси випливає, що 2nk – періоди функції синус і косинус (k 0).

 

Найменшим додатним періодом функції у = tg х є число π.

Справедливе твердження.

Якщо функція у = f(x) періодична і має період Т, то функція у = Af(kx + b), де А,  k,  b — постійні (k 0), також періодична, причому її період дорівнює

IV. Усвідомлення поняття періодичної функції.    Синтез думок

Виконання вправ

1. Обчисліть:  a) sin 1470°; б) tg 1860°;   в) cos 1140°;  r) ctg 1125°Відповідь: а) ;        б) ;      в) ;       г) 1.

2. Знайдіть значення: a) sin ;  б) cos ;  в) tg ; г)ctg. ь: а) ;      б) ;       в) ;      г) 1.

3. Знайдіть найменший додатний період функцій:

а) у = sin2х;      б) у = 3cos 4x;  в) y = 5tg;      г) y=0,6ctg.

Відповідь: а) π;         б) ;       в) ;       г) 4π.

4. Знайдіть значення sin α, якщо:

a) sin (α + 2π) = 0,3;   б) sin (4π - α) = 0,2;  в) sin (α + 6π) = 0,5; г) sin (α - 2π) = 0,1.

Відповідь: а) 0,3;       б) -0,2;     в) 0,5;      г) 0,1.

V. Підсумок уроку. Повторити правила, вивчені на уроці.

VІ. Домашнє завдання. §4, вивчити п.21, №560, №562, №564.

 

УРОК 44

Тема уроку: властивості та  графіки тригонометричних функцій.

Мета уроку: побудова графіків функцій у = sin х, у = cos x,

у = tg х, у = ctg x. формування умінь будувати графіки функцій: у = A sin (kx + b),    у = A cos (kx + b), у = A tg (kx + b), у = A ctg (kx + b), розвивати графічну культуру.

Хід уроку

І. Організаційний момент

І. Перевірка домашнього завдання

1. Один учень відтворює розв'язування вправи №564.

2. Фронтальна бесіда:1) Назвіть явища в природі, які періодично повторюються.

2) Дайте означення періодичної функції.

3) Якщо функція у = f(x) має періодом число Т, то чи буде пе­ріодом цієї функції число 2Т, 3T...? Відповідь обґрунтуйте.

4) Знайдіть найменший додатний період функцій:  a) y = cos; б) y = sin ;   в) у = tg ;  г) у = .

5) Чи періодична функція у = З? Якщо так, то вкажіть пері­од цієї функції.

II. Побудова графіка функції у = sin х.    Керована лекція

Для побудови графіка функції у = sin x скористаємось одиничним колом. Побудуємо одиничне коло радіусом 1 см (2 клі­тинки). Праворуч побудуємо систему координат, як на рис. 57.

На вісь ОХ нанесемо точки ; π; ; 2π (відповідно 3 клітинки, 6 клітинок, 9 клітинок, 12 клітинок).

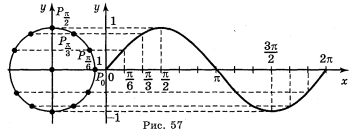
Через те що функція у = sin x періодична з періодом 2π, то для побудови графіка функції у = sin x на всій прямій ОХ досить паралельно перенести побудований графік вздовж осі ОХ на 2π, 4π, 6π... одиниць вліво і вправо (рис. 58).

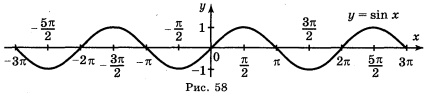
Крива, яка є графіком функції у = sin x, називається синусої­дою.

Виконання вправ

1. Побудуйте графіки функцій.

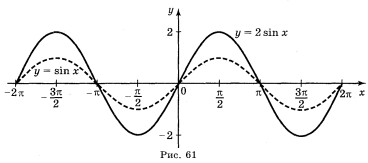
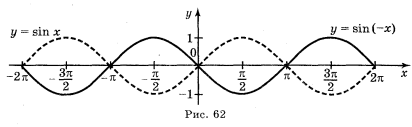
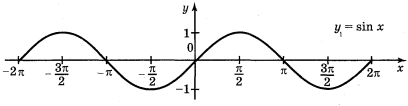
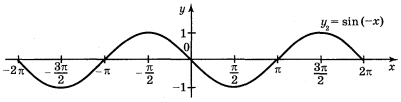
а) у = sin ;             б) у = 2sin х;     г) у = sin (-x).

Відповіді: а) рис. 59;  б)  рис. 61; г) рис. 62.

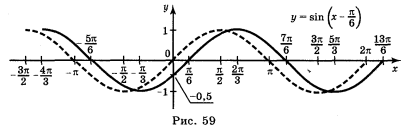
III. Побудова графіка функції  у = cos x.

Як відомо, cos х = sin , тому у = cos x і у = sin — однакові функції. Для побудови графіка функції у = sin скористаємося геометрич-ними перетвореннями графіків: спочатку побудуємо (рис. 63) графік функції     у = sin х, потім у = sin (-х) і наприкінці у = sin  .

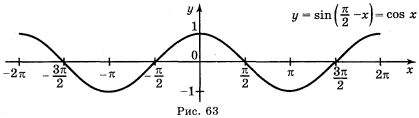
Виконання вправ

1. Побудуйте графіки функцій:

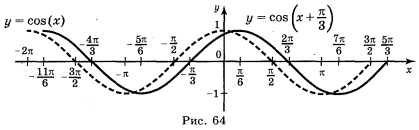
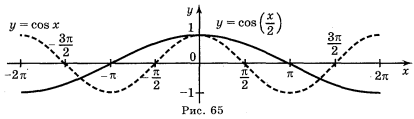
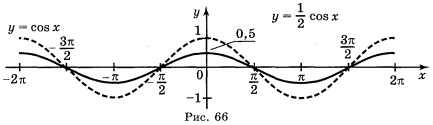
a) y = cos ;      б) y = cos ;  в) y = cos х;   г) у = |cos x|.

Відповідь: а) рис. 64;  б) рис. 65; в) рис. 66; г) рис. 67.

        

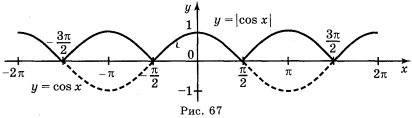
IV. Побудова графіка функції у = tg x.

Графік функції у = tg x побудуємо за допомогою лінії тангенсів на проміжку , довжина якого дорівнює періоду π цієї функції. Побудуємо одиничне коло радіусом 2 см (4 клітинки) і проведемо лінію тангенсів. Праворуч побудуємо систему коор­динат, як на рис. 68.

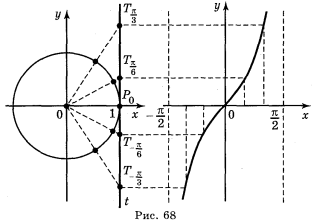
Графік функції у = tg x називається тангенсоїдою.

Виконання вправ

1. Побудуйте графік функцій

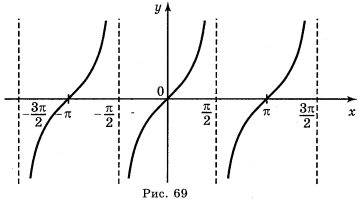
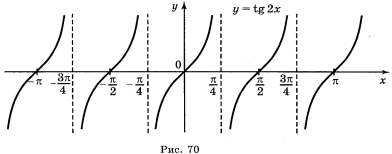
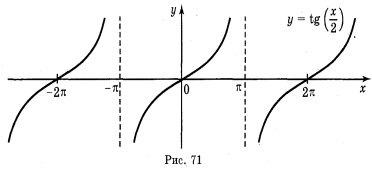
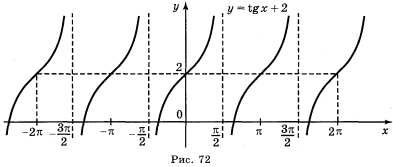
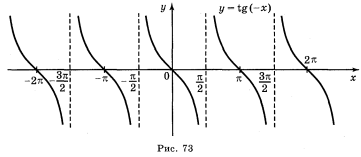
а) у = tg 2х;      б) у = tgx;     в) у = tg x + 2;        г) у = tg (-x).

Відповіді: а) рис. 70;  б) рис. 71; в) рис. 72; г) рис. 73.

 

 

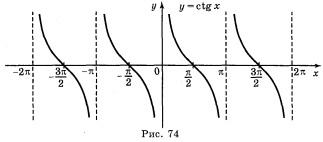
V. Побудова графіка функції у = ctg x.

Графік функції у = ctg x легко одержати, скориставшись формулою ctg x = tg і двома геометричними перетвореннями (рис. 74): симетрія відносно осі ΟΥ паралельне перенесення вздовж осі ОХ на .

IV. Домашнє завдання: §4, вивчити п.22, п23,  №587, №589(1,3,5), №605.

V. Підсумок уроку.

 

УРОК 45

Тема уроку: властивості тригонометричних функцій.

Мета уроку: вивчення властивостей тригонометричних функцій у = sin х, у = cos х, у = tg х, у = ctg x , розвивати логічне мислення, уміння лаконічно висловлювати свої думки.

Хід уроку

І. Організаційний момент.

ІІ. Перевірка домашнього завдання.

Перевірити правильність побудови графіків функцій вправ №587, №605 за рисунками, зробленими до уроку.

IІI. Вивчення властивостей тригонометричних функцій.       Ажурна пилка

1. Вирази sin х і cos х визначені для будь-яких x, оскільки для будь-якого числа х можна знайти координати точки 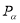, оди­ничного кола. Вираз tg х має смисл при будь-якому x, крім чисел виду х = 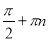, n 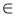Ζ. Вираз ctg x має смисл при будь-якому x, крім чисел виду х = πп, n 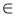Ζ.

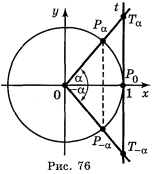
2. Оскільки sin х і cos х — це ордината і абсциса точки одиничного кола, то областю значення синуса і косинуса є про­міжок [-1; 1]. Оскільки tg α — це ордината точки лінії тангенсів, то обла­стю значень тангенса є R. Оскільки ctg α — це абсциса точки   лінії котангенсів, то областю значень котангенса є R.

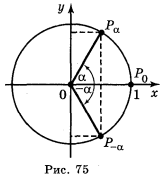
3. Оскільки точки Р_α і Р_-α одиничного кола (рис. 75) симет­ричні відносно осі ОХ, то ці точки мають однакові абсциси і про­тилежні ординати, тобто    sin (-α) = -sin α;  cos (-α) = cos α.

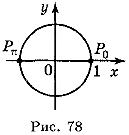
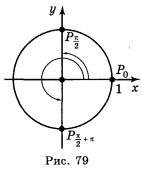4. Ординату, рівну нулю, мають дві точки (рис. 78) одиничного кола: (1; 0) і (-1; 0). Ці точки утворюються із точки (1; 0) поворотом на кути 0, π, 2π, 3π і    т. д., а також на кути -π, -2π... Отже, sin х = 0, якщо х = nk, n Ζ.

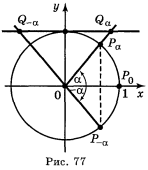
Абсцису, рівну нулю, мають дві точки одиничного кола: (0; 1) і (0; —1). Ці точки Якщо кут α змінюється від 0 до π, то абсциса точки Р_α змен­шується від 1 до -1, тобто cos α спадає на проміжку [0; π], якщо кут α змінюється від -π до 0, то абсциса точки Ρ_α збільшується від -1 до 1, тобто cos α зростає (рис. 81). Враховуючи, що найменший період косинуса є 2π, робимо висновок, що фун­кція cos α спадає на проміжках [2πn; π + 2πn] і зростає на проміжках         [-π + 2πn; 2πn], n Ζ.

 

IV. Застосування властивостей тригонометричних функцій до розв'язування вправ.    Аналіз ситуації

1. Використовуючи властивості функції у = sin x, порівняйте числа:

Відповідь: a) sin > sin ;  б)  sin > sin ;   в) sin 3 > sin 4;           г) sin 1° < sin 1.

2. Розт.числа в порядку зрост.a) sin 20°; sin 85°; sin 30°; б) sin 0,2; sin 0,3; sin 0,1; в) sin 2; sin (-2); sin (-1); sin 1.

Відповідь: a) sin 20°; sin 30°; sin 85°;     б) sin 0,1; sin 0,2; sin 0,3;  в) sin (-2); sin (-1); sin 1; sin 2.

3. Використовуючи властивості функції у = cos x, порівняйте числа:

Відповідь: a) cos 2,52 > cos 2,53;   6) cos (-4,1) > cos (-4);    в) cos 1 > cos 3;    г) cos 4 < cos 5.

4. Розташуйте числа в порядку зростання:

a) cos 13°; cos 53°; cos 23°;   б) cos 0,3; cos 0,6; cos 0,9; в) cos 2; cos 4; cos 6. Відповідь: a) cos 53°; cos 23°; cos 13°; б) cos 0,9; cos 0,6; cos 0,3;  в) cos 4; cos 2; cos 6.

5. Використовуючи властивості функції у = tg x, порівняйте чис­ла:

а) tg (-2,6π) і tg (-2,61π);  б) tg 2,7π і tg 2,75π; в) tg 2 і tg 3; г) tg 1 і tg 1,5.

Відповідь: а) tg (-2,6π) > tg (-2,61π);   б) tg 2,7π < .tg 2,75π;   в) tg 2 < tg 3;    г) tg 1 < tg 1,5.

6. Розташуйте числа в порядку зростання:

a) tg 25°; tg 65°; tg 15°;     б) tg (-1); tg (-2); tg (-3);     в) tg (-5); tg (-3); tg 3.

Відповідь: а) tg 15°; tg 25°; tg 65°;   б) tg (-1); tg (-3); tg (-2);  в) tg 3; tg (-3); tg (-5).

V. Підсумок уроку.

VІ. Домашнє завдання: §4, вивчити п.22, п.23, №581, №584, №602.

 

УРОК 46

Тема уроку:  гармонiчнi коливання

Мета уроку: розглянути приклади реальних процесiв, якi можна описати за допомогою тригонометричних функцiй; сформувати уявлення про гармонiчнi коливання; сформувати вмiння застосовувати тригонометричнi функцiї до опису гармонiчних коливань, розвивати пізнавальний інтерес.

Хiд уроку

І. Органiзацiйний етап

ІІ. Перевiрка домашнього завдання

Перевiряю   виконання  домашніх  вправ у тих учнiв,  якi потребують додаткової  педагогiчної  уваги (збираю  зошити для перевірки).

Картка 1  Побудуйте графiк функцiї та дослiдiть  її   властивостi.

Картка 2   Побудуйте графiк функцiї та дослiдiть  її  властивостi.

ІІІ. Формулювання мети i завдань уроку    

На цьому етапi уроку  проводжу  бесiду про те, що iснує багато реальних процесiв, якi описуються за допомогою тригонометричних функцiй. Наприклад, висота пiдйому тiла, кинутого пiд кутом до горизонту обчислюється за формулою  , а дальнiсть польоту — за формулою .

Також у навколишньому середовищi   дуже  поширенi, так  званi,  коливальнi  рухи. Уявлення про них дають, наприклад, океанськi хвилi, маятниковi годинники, гойдалки, нервові  iмпульси, крила метелика, рух поплавка вудочки тощо. Багато з них можна описати за допомогою гармонічних коливань. З’ясувати, як    тригонометричнi функцiї використовуються для опису коливальних процесiв, — це завдання та дидактична мета уроку.

IV. Актуалiзацiя опорних знань

1. Чому дорiвнює перiод функцiї:а) ; б) ; в) ;
г) ?

2. . Обчислiть: ; ; .

3. . Обчислiть: ; ; .

V. Засвоєння знань   

Керована лекція, учні готували реферати

План вивчення нового матерiалу

1. Поняття гармонiчних коливань.  

2. Параметри, що визначають гармонiчнi коливання.

VI. Формування вмiнь

1. Координата (у см) тiла, що рухається, змiнюється за указаним законом. Знайдiть амплiтуду, перiод, частоту коливання. Обчислiть координату тiла в момент часу , якщо:

а) , ; б) , .

2. Знайдiть амплiтуду, перiод, частоту сили струму, якщо вона змiнюється за законом (силу струму вимiряно в амперах, час — у секундах): а) ; б) .

Конспект                 Гармонiчнi коливання

1. Гармонiчними  коливаннями називаються процеси, якi описуються  функцiєю, що задається формулою або . Такою функцiєю описується, наприклад, координата кульки, що підвішена на пружинi. Кажуть, що кулька здiйснює  гармонічні  коливання.

2. Параметри , , повнiстю визначають гармонiчне коливання i мають спецiальнi назви:

називають амплiтудою коливання; — циклiчною (кутовою) частотою коливання; — початковою фазою коливання (зазвичай ).  Амплiтуда характеризує величину найбiльшого вiдхилення вiд положення рiвноваги.   Число є кiлькiстю повних коливань за одиниць часу. Число j характеризує початкове положення точки.     Перiод функцiй і , який дорiвнює , називають перiодом гармонiчного коливання.

Приклад. Запишемо рiвняння гармонiчного коливання, якщо його амплiтуда дорiвнює 0,6, перiод — 0,02с, початкова фаза — . За умовою ; , звідки ; . Тодi рiвняння має вигляд: .

3. Знайдiть амплiтуду, перiод i частоту напруги, якщо вона змiнюється за законом (напругу вимiряно у вольтах, час — у секундах): а) ; б) .

4. За графiком гармонiчного коливання, зображеного на рисунку, визначте амплiтуду сили струму, перiод коливання. Запишiть закон залежностi сили струму вiд часу.

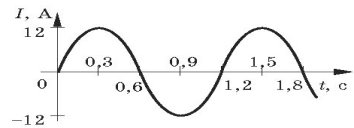
5. Точка виконує гармонiчне коливання за законом . Побудуйте графiк цього гармонiчного коливання.

VII. Пiдсумки уроку

У який найближчий момент часу, вважаючи вiд початку руху, змiщення точки, що здiйснює гармонiчне коливання за законом

, а) буде максимальним; б) дорiвнюватиме нулю; в) дорiвнюватиме 2,5; г) дорiвнюватиме –5?

VIII. Домашнє завдання: §4, вивчити п.30, №764, №766. 

Засвоїти змiст понять, якi були розглянутi на уроцi.

1. Координата (у см) тiла, що рухається, змiнюється за указаним законом. Знайдiть амплiтуду, перiод, частоту коливання. Обчислiть координату тiла в момент часу , якщо: а) , ; б) , .

2. Знайдiть амплiтуду, перiод, частоту сили струму, якщо вона змiнюється за законом (силу струму вимiряно в амперах, час — у секундах): а) ; б) .

3. Знайдiть амплiтуду, перiод i частоту напруги, якщо вона змiнюється за законом (напругу вимiряно у вольтах, час — у секундах): а) ; б) .

4. За графiком гармонiчного коливання, зображеного на рисунку, визначте амплiтуду напруги, перiод коливання. Запишiть закон залежностi напруги вiд часу.

 

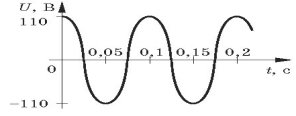
УРОК 47

Тема уроку: розв’зування вправ.  Самостійна робота.

Мета уроку: повторити, систематизувати та узагальнити знання учнiв щодо змiсту вивчених у роздiлi понять; провести огляд типових задач iз цiєї теми; удосконалити вмiння розв’язувати задачi. Розвивати стійкі обчислювальні навички, культуру математичної мови.

Хiд уроку

І. Органiзацiйний етап

ІІ. Перевiрка домашнього завдання

Збираю зошити для перевiрки та оцiнювання якостi виконання домашньої роботи.

ІІІ. Формулювання мети i завдань уроку, мотивація навчальної дiяльностi

Виникає необхiднiсть повторення, узагальнення та систематизації знань i вмiнь, набутих учнями пiд час вивчення попередніх тем. Таке формулювання мети створює вiдповiдну мотивацiю діяльності учнiв.

ІV. Повторення та систематизацiя знань

Мозковий штурм

1. Сформулюйте означення кута в 1 радiан. Пояснiть, як за радiанною мiрою кута знайти його градусну мiру i, навпаки — за градусною мiрою кута знайти його радiанну мiру.

2. Сформулюйте означення тригонометричних функцiй довiльного кута, використовуючи коло радiуса R iз центром у початку координат або одиничне коло. Що називають тригонометричними функцiями числового аргумента?

3. Укажiть область визначення та множину значень кожної з тригонометричних функцiй.

4. Назвiть i обґрунтуйте знаки тригонометричних функцiй у кожнiй з координатних чвертей.

5. Якi спiввiдношення пов’язують тригонометричнi функцiї одного аргумента?

6. Сформулюйте означення перiодичної функцiї. Обґрунтуйте перiодичнiсть тригонометричних функцiй. Укажiть найменший додатний перiод кожної з тригонометричних функцiй. Якi з тригонометричних функцiй є парними, а якi — непарними?

V. Самостійна робота 

Варiант 1

1. Знайдiть: а) градусну мiру кута, радiанна мiра якого дорiвнює: 4,5; ; ;

б) радiанну мiру кута, градусна мiра якого дорiвнює: ; ; .

2. Знайдiть значення виразу: а) ; б) .

3. Знайдiть значення тр. функцiй кута , якщо вiдомо, що і .

4. Доведiть тотожнiсть .

5. Знайдiть найменший додатний перiод функцiї:   а) ; б) .

6. Побудуйте графiк функцiї . Знайдiть промiжки зростання, спадання та нулi цiєї функцiї.

Варiант 2       

1. Знайдiть: а) градусну мiру кута, радіанна мiра якого дорiвнює: 2,5; ; ;

б) радiанну мiру кута, градусна мiра якого дорiвнює: ; ; .

2. Знайдiть значення виразу: а) ; б) .

3. Знайдiть значення тригонометричних функцiй кута , якщо вiдомо, що і .

4. Доведiть тотожнiсть .

5. Знайдiть найменший додатний перiод функцiї: а) ; б) .

6. Побудуйте графiк функцiї . Знайдiть промiжки зростання, спадання та нулi цiєї функцiї.

VI. Пiдсумки уроку

VII. Домашнє завдання: §4, повторити п.22, п.23, п.30, №604, №605, №606.

 

УРОК 48

Тема уроку: формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і по­ловинного аргументу.

Мета уроку: вивчення формул тригонометричних функцій суми і різниці двох чисел, формул тригонометричних функцій подвійного і половинного аргументу. Фор­мування умінь застосовувати вивчені формули для спрощення виразів та обчислень. Розвивати логічне мислення, пам’ять, навички самостійного мислення.

Хід уроку

І. Перевірка домашнього завдання.

Розв'язання вправ, аналогічних до домашніх.

II. Сприймання і усвідомлення формул суми і різниці двох чисел.   Керована лекція

1. Розглянемо, як пов'язані косинус різниці двох чисел із сину­сом і косинусом цих самих чисел.

соs (α – β) = соs α · соs β + sіn α · sіn β.             (1)

Користуючись одержаною формулою, можна одержати інші формули:

соs (α + β) = соs α · соs β – sіn α · sіn β;                (2)

sіn (α + β) = sіn α · соs β + соs α · sіn β;                (3)

sіn (α – β) = sіn α · соs β – соs α · sіn β;                 (4)

      (5)                              (6)

 

Виконання вправ

1. Знайдіть значення виразів:

а) соs 42° соs 18° – sіn 42°sіn 18°; б) ;  в) sіn 56° соs 34° + соs 56° sіn 34°; 

г) ;   д) ;  є) .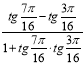

2. Спростіть вирази:

а) sіn(α + β) – sіn α · соs β;   б) .

 Відповідь: а) соs α · sіn β; б) sіn 2α.

III. Сприймання і усвідомлення тригонометричних функцій подвійного аргументу.

Демонструється таблиця “Тригонометричні функції подвійного аргументу”

Тригонометричні функції подвійного аргументу sіn 2α = 2sіn α соs α соз 2α = соs2 α - sіn2 α

 

Виконання вправ

1. Обчисліть:

а) 2sin15° соs15°;  б) соs²15° – sіn²15°;  в) ;  г) (соs 75° – sіn 75°).

Відповідь: а) ; б)  ; в) ; г) .

 

2. Обчисліть sіn 2α, якщо а) sin α = ; < α < π;  б) соs α = ; π < α < .

Відповідь: а)  ; б) .

IV. Сприймання і усвідомлення тригонометричних функцій половинного аргументу.

соs α = соs² – sіn² .   (1)       1 = соs² + sin².    (2)

1+ соs α = 2соs² ;    (3)

1 – соs α = 2sіn² .   (4)                

(5)              

(6)

Виконання вправ  

 1. Знайдіть числові значення виразу:

а) 2соs²   – 1;    б) 1 – 2sin² ;    в) + 2sіn²15°;     г) - + 2соs²15°.

  Відповідь: а) ;   б)  ;      в) 1;   г) 1.

2. Нехай соs α = 0,6 і 0 < α < . Обчисліть:  а) sin ;  б) соs ;   в) tg .

Відповідь: а) ;     б) ;    в) .

V. Підведення підсумків уроку.

VI. Домашнє завдання: §4, вивчити п.25, п.26, №642, №644, №648, №695.

 

 

УРОК 49

Тема уроку: формули перетворення  суми і  різниці

однойменних тригономет­ричних функцій на добуток.

Мета уроку: вивчення формул суми і різниці однойменних

тригонометричних функцій. Формування умінь учнів застосовувати вивчені формули для спро­щення виразів та обчислень. Розвивати стійку увагу, пам’ять, прагнення до самореалізації.

Хід уроку

І. Організаційний момент.

ІІ. Перевірка домашнього завдання.

1. Два учні на дошці розв'язують вправи домашнього завдання.

2. Розв'язування аналогічних вправ. Спростіть вирази:            Робота в парах

а) ;          б) ;

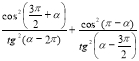в) ;    г) .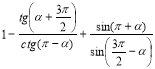

 Відповідь: а) соs² α;    б) ;   в) 1;   г) tg α.

ІII. Повідомлення теми і завдань уроку.

IV. Сприймання і усвідомлення нового матеріалу.

 

Формули перетворення суми у добуток ; ; ;.

 

1. Виведемо формулу перетворення суми синусів в добуток.       Навчаючи-вчуся

Позначимо ,  , тоді α + β = x, α – β = y, і тому

1) sin х + sin y = sin(α + β) + sin(α - β) = sin α · соs β + соs α · sіnβ + sin α · cоs β –   – cos α · sіn β = 2sіn α  · соs β = 2sіn соs . Отже, сума синусів дорівнює подвоєному добутку синуса півсуми на косинус піврізниці.

Для суми косинусів маємо:

2) соs х + соs у = соs(α + β) + соs(α – β) = соs α  соs β – sіn α sin β + соs α  соs β + + sіn α  sіn β = 2 соs α соs β = 2 соs соs . Отже, сума косинусів дорівнює подвоєному добутку косинуса півсуми на косинус піврізниці.

Для різниці косинусів маємо:

3) соs х – соs у = соs(α + β) – соs(α – β) = соs α соs β - sіn α sin β – соs α соs β –    – sіn α sіn β = – 2 sin α sin β = 2 sin sin Отже, різниця косинусів дорівнює числу, протилежному подвоєному добутку синуса півсуми на синус піврізниці.

4) sin х – sin y = sin х + sin(-y) = 2 sinсоs .  Отже, різниця синусів дорівнює подвоєному добутку синуса пів­різниці на косинус півсуми.

V. Виконання вправ

1. Спростіть вирази:

а) – ;   б)  – .

в) sіn α · ;  г) +.

Відповідь: а) sin β; б) sin 2α; в) ; г) соs α.

2. Обчисліть: а) соs 22° – соs 38°; б) sin 5° + sin 55°.  

Відповідь: а) sіn 8°;     б) соs 25°.

3. Перетворіть в добуток:

а) соs 2α + соs 14α + соs 6α + соs 10α;

б) sin 4β + sin 10β + sin 22β + sin 16β .

Відповідь: а) 4соs 2α соs 4α соs 8α; б) 4 соs 3β соs 6β sіn 13β.

4. Доведіть тотожність:

а) ; б) .

VІ. Підведення підсумків уроку.

VІІ. Домашнє завдання: §4, вивчити п.28, №734, №736, №742(1).

 

УРОК 50

Тема уроку:  перетворення добутку тригономет­ричних функцій у суму.

Мета уроку: вивчення формул перетворення до­бутку тригонометричних функцій у суму. Формування умінь учнів застосовувати вивчені формули для спро­щення виразів та обчислень. Розвивати логічне мислення, пам’ять, творчі здібності учнів.

Хід уроку

І. Організаційний момент

ІІ. Перевірка домашнього завдання.

1. Два учні на дошці розв'язують домашні вправи.

2. Розв'язування аналогічних вправ.

IІI. Повідомлення теми і завдань уроку.

На сьогоднішньому уроці будемо вивчати формули перетворення добутку тригонометричних функцій у суму. Навчимось застосовувати вивчені формули для спрощення виразів та обчислень.

IV. Сприймання і усвідомлення нового матеріалу.

  Розглянемо формули перетворення

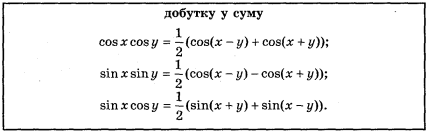
Для одержання формул перетворення добутку у суму випи­шемо підряд чотири формули:

sin(x + у) = sin x cos у + cos x sin у;    (1)

sin(x – у) = sin x cos у – cos x sin у;    (2)

cos(x + у) = cos x cos у – sin x sin у;    (3)

cos(x – у) = cos x cos у + sin x sin у.    (4)

 

Віднявши почленно із рівності (4) рівність (3), одержимо:

cos(x – у) – cos(x + у) = 2 sin x sin у

або

sin x sin у = (cos(х – у) – cos(x + y))

Добуток синусів двох чисел дорівнює піврізниці косинуса різниці і косинуса суми цих чисел.

 

Додавши почленно рівності (4) і (3), маємо:

соs(x – у) + соs(х + у) = 2 соs х соs у

або

cos x cos у = (cos(x – у) + cos(х + у))

Добуток косинусів двох чисел дорівнює півсумі косинуса різниці і косинуса суми цих чисел.

Додавши почленно рівності (1) і (2), одержимо

sin(x – у) + sin(х + у) = 2 sin x cos у

або

sin x cos у = (sin(x – у) + sin(x + у))

Добуток синуса одного числа на косинус другого числа дорівнює півсумі синуса різниці і синуса суми цих чисел.

V. Виконання вправ

1. Спростити: sіn α · 2. Спростіть виразта обчисліть,  якщо α = -.

3. Обчисліть (не використовуючи таблиці і мікрокалькулятор) sin 75°  4. Обчисліть  4 sin 15° sin 75° – 1.

Розв'язання

1спосіб

                 

2 спосіб 0

 

VІ. Підведення підсумків уроку.

VІІ. Домашнє завдання: §4, вивчити п.29, повторити п.28, №749, №753, №755.

 

УРОК 51

Тема уроку: тотожні перетворення тригонометричних виразів.

Мета уроку: виробити навички та вдосконалити вміння учнів, набутих пiд час вивчення теми, розвивати логічне мислення, творчі здібності учнів.

Хiд уроку

І. Органiзацiйний етап

ІІ. Перевiрка домашнього завдання

Зiбрати зошити iз виконаною домашньою роботою. Оцiнки за цю роботу врахувати пiд час виставлення тематичного бала.

ІІІ. Формулювання мети та завдань уроку

На цьому уроці повторюємо, узагальнюємо та систематизуємо знання і вміння, набуті під час вивчення даної теми.

ІV. Розв’язування вправ на повторення.       Мозковий штурм

1. Знайдiть: а) градусну мiру кута, радiанна мiра якого дорiвнює: 4,5; ; ;

б) радiанну мiру кута, градусна мiра якого дорiвнює: ; ; .

2. Знайдiть значення виразу: а) ;

б) .

3. Знайдiть значення тр. функцiй кута , якщо вiдомо, що і .

4. Доведiть тотожнiсть  .

5. Знайдiть найменший додатний перiод функцiї:

а) ; б) .

6. Спростiть вираз: а) ;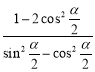

б) .

7. Доведiть тотожнiсть .

8.  Обчислiть: а) ; б) ; в) .

V. Пiдсумки уроку

VI. Домашнє завдання: §4, повторити п.п. 24-30,  №692(10-12),  №718(3-5).

 

УРОК 52

Тема уроку: пiдсумковий урок iз теми «Тригонометричнi вирази». Розв’язування вправ.  Самостійна робота.

Мета уроку: повторити, систематизувати та узагальнити знання учнів тригонометричних формул  та наслiдкiв iз них; провести огляд типових задач iз цiєї теми; удосконалити вмiння розв’язувати задачi. Провести роботу з корекцiї знань та вмiнь учнiв з метою усунення причин найтиповiших помилок. Пiдготувати учнiв до виконання завдань контрольної роботи. Розвивати логічне мислення, стійкі обчислювальні навички, швидкість реакції, кмітливість, допитливість.

Хiд уроку

І. Органiзацiйний етап

ІІ. Перевiрка домашнього завдання

Збираю зошити для перевiрки та оцiнювання якостi виконання домашньої роботи.

ІІІ. Формулювання мети i завдань уроку, мотивацiя навчальної дiяльностi

Основна дидактична мета та завдання на урок випливають iз його мiсця в темi.  Оскiльки урок є пiдсумковим, то виникає необхiднiсть повторення, узагальнення та систематизацiї знань i вмiнь, набутих учнями пiд час вивчення зазначеної теми. Таке формулювання мети створює вiдповiдну мотивацiю дiяльностi учнiв.

ІV. Повторення та систематизацiя знань    

Контрольнi запитання до теми         Мозковий штурм

1. Запишiть тригонометричнi формули додавання та наведiть словесне формулювання цих формул. Наведiть приклади застосування формул додавання.

2. Обґрунтуйте формули подвiйного аргумента. Наведiть словесне формулювання цих формул. Наведiть приклади їх застосування.

3. Сформулюйте правило зведення тригонометричних функцiй вiд аргументiв виду і , до тригонометричних функцiй вiд аргумента .

4. Запишiть формули перетворення суми й рiзницi тригонометричних функцiй на добуток. Наведiть словесне формулювання цих формул. Наведiть приклади їх застосування.

5. Обґрунтуйте формули перетворення добутку тригонометричних функцiй на суму. Наведiть словесне формулювання формул. Наведiть приклади застосування цих формул.

V. Самостійна робота (із взаємоперевіркою та колективним обговоренням типових помилок)

1. Обчислiть:

а) ; б) ; в) .

2. Знайдiть значення виразу .

3. Спростiть вираз:

а) ; б) .

4. Доведiть тотожнiсть .

5. Знайдiть перiод функцiї .

6. Знайдiть , якщо .

VI. Пiдсумки уроку

Пiдсумком уроку узагальнення й систематизацiї знань i вмiнь учнiв є здiйснення учнями необхiдної частини свiдомої розумової дiяльностi (рефлексiї), усвiдомлення кожним учнем особистих успiхiв та, найголовнiше,—проблем, над якими слiд ще попрацювати.

VII. Домашнє завдання: повторити §4, п.п.24-30, №692(14,15), №718(1,2), 752(1).

 

 

УРОК 53

Тема уроку: контрольна робота з теми «Тригонометричні вирази» (№6)

Мета уроку: перевiрити рiвень знань і вмiнь учнiв, набутих пiд час вивчення теми «Тригонометричнi формули та наслiдки з них», розвивати самостійність, старанність, наполегливість у досягненні мети.

Хiд уроку

І. Органiзацiйний етап

ІІ. Перевiрка домашнього завдання

Зiбрати зошити з виконаною домашньою роботою.  Оцiнки за цю роботу врахувати пiд час виставлення тематичного бала.

ІІІ. Формулювання мети та завдань уроку

Ще раз наголошую, що метою контрольної роботи є демонстрацiя учнями своїх досягнень, а саме: показати знання тригонометричних формул та наслiдкiв iз них, вмiння застосовувати цi знання до розв’язування задач.

ІV. Текст контрольної роботи №6

Варiант 1

1. Обчислiть: а) ; б) ; в) .

2. Знайдiть значення виразу .

3. Спростiть вираз:   а) ; б) .

4. Доведiть тотожнiсть .

5. Знайдiть перiод функцiї .

6. Доведiть нерiвнiсть .

Варiант 2

1. Обчислiть: а) ; б) ; в) .

2. Знайдiть значення виразу .

3. Спростiть вираз:   а) ;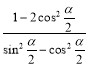

б) .

4. Доведiть тотожнiсть .

5. Знайдiть перiод функцiї .

6. Доведiть нерiвнiсть .

V. Пiдсумки уроку

На цьому етапi уроку, пiсля того як будуть зiбранi зошити, вiдповiдаю на запитання учнiв, якi виникли в процесi виконання контрольної роботи.

VI. Домашнє завдання: Виконати аналiз контрольної роботи.