Тема уроку: Теорема Фалеса. Трапеція. Вписані та описані чотирикутники. Розв’язування задач.

Тема уроку: Теорема Фалеса. Трапеція. Вписані та     описані чотирикутники. Розв’язування задач.

Мета уроку: повторити, систематизувати та узагальнити означення, ознак та властивостей трапеції; теореми Фалеса; означення та властивостей кутів у колі; означення вписаних та описаних чотирикутників, їх властивостей та ознак. Розвивати пам’ять, логічне мислення учнів, формувати вміння аналізувати інформацію. Виховувати дисциплінованість, самостійність, відповідальність.

       Тип уроку: узагальнення знань, умінь, навичок

       Обладнання: кросворд, комп’ютерна презентація за програмою Pоwer Point,  індивідуальні завдання, тестові завдання.

Епіграф уроку:

Серед рівних розумом – за однакових умов –

переважає той, хто знає геометрію.

Б. Паскаль

Девіз  уроку:

Тільки після невтомної праці

з’явиться талант.

                                    Народна мудрість

ХІД УРОКУ

І. Організаційний етап.

ІІ. Перевірка домашнього завдання.

Фронтальне опитування

Кросворд

Завдання:

1) Плоский кут із вершиною в центрі кола називається

(Центральним)

2) Чотирикутник називається … навколо кола, якщо всі його сторони дотикаються до цього кола

(Описаним)

3) Ім’я вченого, який довів теорему про паралельні прямі, які перетинають сторони кута

(Фалес)

4) Середня лінія трикутника паралельна одній з його сторін і дорівнює цієї сторони

(Половині)

5) Вписаний кут вимірюється половиною …., на яку він спирається

(Дуги)

6) Чотирикутник, у якого дві сторони паралельні, а дві інші не паралельні

(Трапеція)

7) Вписані кути що спираються на одну дугу, …

(Рівні)

8) Якщо ви все виконали, то ви...

(Молодці)

ІІІ. Мотивація навчальної діяльності.

       На попередніх уроках ми вивчили теорему Фалеса, види трапецій та їх властивості, середню лінію трикутника і середню лінію трапеції, означення та ознаки вписаних і описаних чотирикутників; навчилися використовувати вивчений матеріал при розв’язуванні задач. Мета сьогоднішнього уроку – повторити, узагальнити та систематизувати ці знання, і таким чином підготуватися до контрольної роботи.

І розпочати наш урок я хочу із казки «Пряник і Колосок», яку написав своєму сину відомий педагог В.О.Сухомлинський.

Вранці, до сходу сонця Людина взяла білий пряник і пішла в поле. Зірвала колосок у полі, вийняла з нього зернята, спробувала на зуб, посміхнулася і заховала колосок у кишеню. Ось там і зустрілися Пряник і Колосок.

• Хто ти такий? – запитав Пряник.
• Я – Колосок.
• Ой, який ти колючий! Яка з тебе користь?

Посміхнувся Колосок, поворухнув своїми вусиками і відповів:

• Без мене не було б ні хліба, ні сухаря, ні тебе, Прянику.
• Отже, - каже Пряник, - все від тебе. Але хто ж над тобою старший?
• Праця, - відповідає Колосок, - вона все дає. Але праця в руках людини. Праця і Людина – найголовніші.

      Отже, я вас закликаю до праці, до праці наполегливої і творчої, щоб пізнавати істину міркувань. Народна мудрість говорить: «Тільки після невтомної праці з’явиться талант». Я думаю, що наш урок буде тому підтвердженням. І всі ми покажемо, які ми працьовиті, наполегливі і талановиті.

 IV. Актуалізація опорних знань.

         Якщо немає запитань стосовно домашньої роботи, то я пропоную розв’язати аналогічні завдання біля дошки:

1. Індивідуальні завдання.

          Задача 1.

     Знайдіть середню лінію рівнобічної  трапеції з бічною стороною 5 см і периметром  26 см.

           Задача 2.

     Знайдіть основи трапеції, якщо одна з них більша за іншу на 6 см, а середня лінія трапеції дорівнює 5 см.

2. Питання до класу.

1. Який чотирикутник ми називаємо трапецією? Які види трапеції ви знаєте?
2. Чому дорівнює середня лінія трапеції (трикутника)?
3. Які кути називаються вписаними у коло, а які центральними?
4. Сформулюйте властивості вписаних кутів.
5. В якому випадку чотирикутник можна вписати у коло, а в якому – описати навколо кола?

      Усні вправи.

1. Знайти невідомий відрізок  х(рис.1):

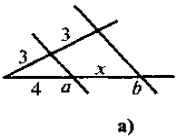
Рис. 1

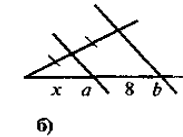
 2.На якому із наведених рисунків зображено чотирикут­ник ABCD:

а) вписаний у коло;

б) описаний навколо кола?

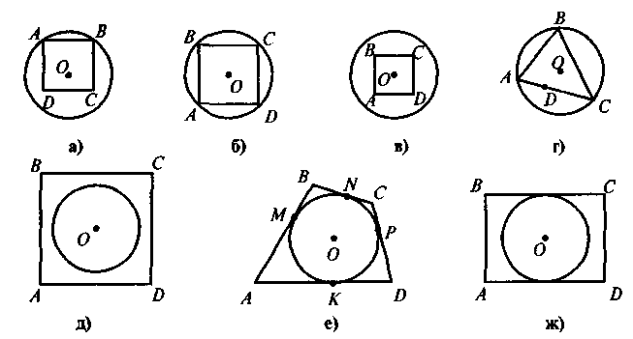
Рис.2

3. Знайдіть довжину відрізка  х (рис. 3):

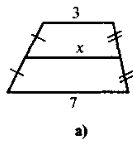
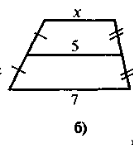
Рис.3

4. Знайдіть на рисунку 4  помилки (поясніть).

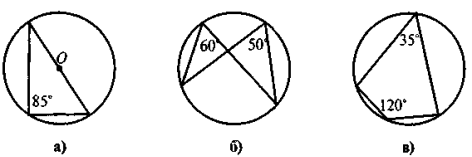
Рис.4

V. Застосування знань і вмінь.

     Розв’язування задач з підручника № 203 с. 59 (колективна робота)

                 Задача 1

     У рівнобічній  трапеції діагональ завдовжки 4 см утворює з основою кут 60⁰  . Знайдіть середню лінію трапеції.

 Тестові завдання

І варіант                                                  ІІ варіант

1. Центральний кут у колі дорівнює

120⁰                                                           160⁰.

Тоді градусна міра відповідного вписаного кута становить:

2. Основа рівнобедреного трикутника дорівнює

18см                                                                  22см

Чому дорівнює середня лінія, паралельна цій основі?

3. Два послідовні кути вписаного чотирикутника дорівнюють

80⁰ і 120⁰                                                    60⁰ і 100⁰.

Знайти два інші кути.

4. Чи правильно, що

Навколо кожної трапеції                               Навколо кожного прямокутника

можна описати коло?                                    можна описати коло?

5. Три послідовні сторони описаного чотирикутника дорівнюють

2см; 3см; 4см                                                3см; 4см; 5см

Знайдіть четверту сторону.

6. Основи трапеції дорівнюють

5см і 7см                                                          7см і 9см

Чому дорівнює довжина середньої лінії?

7. Вписаний кут становить

70⁰                                                                    50⁰

Знайдіть величину відповідного центрального кута.

8. Знайти периметр трикутника, якщо його середні лінії дорівнюють:

4см; 5см; 6см                                         5см; 6см; 7см.

VI. Підсумки уроку.

       Таким чином ми повторили весь необхідний теоретичний матеріал та основні типи задач, що розглядаються в цьому розділі. Я думаю, що ще попрацювавши вдома ви належним чином підготуєтеся до контрольної роботи. А зараз з метою перевірки ваших знань та вмінь проведемо таку невелику роботу із взаємоперевіркою.

 Встановити відповідність:

1. Описаний навколо кола чотирикутник

2. Вписаний у коло чотирикутник

3. Рівнобічна трапеція

4. Вписаний у коло кут

А. Сума протилежних кутів дорівнює 180⁰

Б. Бічні сторони  рівні

В. Суми протилежних сторін рівні

Г. Дорівнює відповідному      центральному куту

Д. Вимірюється половиною дуги     кола, на яку він спирається

VIІ. Завдання додому.

1. Повторити §4 - §7.

2. Виконати задачі для підготовки контрольної роботи  №2 с.87