Тема відкритого уроку: Показникова функція, її графік та властивості


вчитель математики Іванова І.В.
Тема відкритого уроку: Показникова функція, її графік та властивості.
Мета уроку: засвоєння учнями поняття показникової функції, її загальних властивостей; графіку; з’ясувати практичне застосування; формувати свідоме розуміння учнями значення математики під час вивчення явищ природи та фізичних процесів; розвивати навички самостійності, кмітливості, оперативності при виконанні вправ, виховування уваги, швидкості реакцій, зібраності, організованості, стимулювати розвиток логічного мислення.
Хід уроку
Організаційний момент
Актуалізація опорних знань
Починаючи з 7 – го класу ви розглядаєте на уроках алгебри багато залежностей між величинами, позначеними буквами, серед яких зустрічалися як сталі, так і зміні. Особливе місце займає поняття функції, тобто залежності змінної у від змінної х, коли кожному значенню аргументу х відповідає одне тільки значення у.
Проведемо «Мозковий штурм» під девізом «Хай живе теорія!». Продовжити речення:
1) Якщо кожному значенню змінної х з деякої множини D відповідає єдине значення змінної у, то таку відповідність називають … (функцією)
2) х називають незалежною змінною, або … (аргументом)
3) Функцію можна задати за допомогою … (таблиці, графіка, формули.)
4) Множину D називають областю … (визначення) 5) Область визначення функції – це …(всі значення, які може приймати аргумент змінна x). 6) Множину Е називають областю … (значень)
7) Область значень функції - це … (всі значення, які може приймати функція (змінна y) при всіх x із області визначення функції).
8) Яку мають назву зростаючі, спадні, не зростаючі, не спадні функції? (монотонні)
9) На деякому проміжку виконуються умови: у(3)>у(-8). у(1)>у(8). у(3)=у(-8). Які це функції,зростаючи чи спадні? Чому?
10) Що називається графіком функції? (Графіком функції y = f(x) називається множина всіх точок координатної площини (x, f(x)), у яких абсциси належать області визначення функції, а ординати дорівнюють відповідним значенням функції).
|
|
|
|
|
|
|
Функція №1 |
Функція №3 |
Функція №5 |
|
Функція №7 |
|
Y
|
|
|
X |
X
|
|
Функція №2 |
Функція №4 |
Функція №6 |
|
Функція №8 |
11) Перед вами картки, на яких накреслені графіки деяких функцій. З’ясувати, чи всі графіки відповідають функціям чи є зайвий малюнок, чому?
12) З’ясувати, чи є серед них графік лінійної функції? Назвати формулу? 13) Що є графіком кожної лінійної функції? (пряма) 14) Чи є серед графіків окремі випадки степеневої функції? Формула, назва графіку.
15) Як називають графік функції у=х2? у=х3 (парабола)
16) Як називається добуток кількох рівних множників? (степінь)
17) Чому дорівнює нульовий степінь числа? (1)
Мотивація навчальної діяльності
В житті дуже важливо берегти і раціонально використовувати матеріальні цінності. Зокрема, чим економніше ми будемо використовувати вже створені засоби праці, тим менша частина суспільного продукту потрібна буде для їх відшкодування, тим більше буде зекономлено матеріальних цінностей для народного господарства. Для прикладу розглянемо задачу:
Фермер отримав новий інвентар (сівалка, культиватори) для обробітку ґрунту на суму 8000 грн. Яка буде вартість цього інвентарю через рік, 2 роки, t років, коли щороку на амортизацію відраховується 10% його вартості?
Розв’язання:
Вартість інвентарю через рік становитиме 90% початкової вартості, тобто 8000×0,9, через два роки - 8000×0,9², через t років 80000×0,9 t .
Ми бачимо: чим більше значення t, тобто чим довше ми експлуатували техніку (що можливо тільки при бережливому відношенні до неї), тим буде менша її ціна! Зверніть увагу, що основа степеня 0<0,9<1. А як би у нас при розв’язуванні зовсім іншої задачі в основі степеня було б число, більше одиниці, як ви вважаєте, ця величина збільшувалася б із збільшенням значення t чи зменшувалася? (Збільшувалася)
При розв’язуванні цієї задачі і багатьох інших задач народного господарства, фізики, соціальних наук ми зустрічаємося з формулою, для обчислення значення якої сталий множник доводиться множити на степінь сталої зі змінним показником. Яка має цілком певне додатне значення. Найпростішим випадком таких залежностей є функція вигляду y=aх, яку називають показниковою.
Розглянемо ще один приклад.
Нині багато говорять про інформаційний бум. Стверджують, що кількість інформації подвоюється кожні десять років. Зобразимо цей процес у вигляді графіка деякої функції, де х – десятиліття, у – обсяг інформації.
Візьмемо обсяг інформації в деякий початковий рік за 1. Удвічі більший відрізок поставимо над одиничною оцінкою, вважаючи, що оцінка відповідає першому десятку років. Удвічі більший відрізок відповідає другому десятку років, ще вдвічі більший – третьому і т.д. Обране нами значення аргументу є елементами арифметичної прогресії: 2, 4, 8, … . Спробуємо
|
х |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
у=2х |
|
|
|
1 |
2 |
4 |
8 |
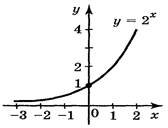 уявити собі яким був обсяг інформації до року, прийнятого за початковий. Додамо до отриманих значень результати з від`ємним аргументом. Отримали функцію у=2х
уявити собі яким був обсяг інформації до року, прийнятого за початковий. Додамо до отриманих значень результати з від`ємним аргументом. Отримали функцію у=2х
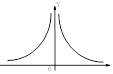
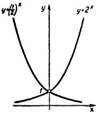
Побудуємо на координатній площині точки з таблиці і з'єднаємо ці точки плавною лінією. Перед нами графік показникової функції у=2х. Головна особливість графіка цієї функції – її крутизна.
Графік показникової функції називають експонентою, а процеси, які можна описати функцією виду у=ах, експоненціальними процесами.
Показникова функція зустрічається в описі процесів, у яких швидкість зміни величини пропорційна до самої величини. Ще Леонард Ейлер писав: «Деякі види функцій, що найбільше використовуються, насамперед показникові, відкривають доступ до багатьох досліджень». За таким правилом розмножується все живе. Так за законом експоненціального зростання збільшується колонія мікробів у чашці Петрі. За таким самим законом плодилися кролі, які за короткий термін заполонили Австралію. Прикладом показникового спадання є хід хімічної реакції: швидкість хімічної реакції пропорційна до кількості речовин, що реагують. Швидкість радіоактивного розпаду також пропорційна до кількості атомів, що не розпалися.
Вкажемо деякі випадки органічної зміни величин:
Ø при проходженні світла через мутне середовище, сила світла на проміжках даної довжини зменшується в одному і тому самому відношенні;
Ø тиск повітря при даній різниці висот зменшується в одному і тому самому відношенні;
Ø швидкість тіла, що рухається в середовищі, опір якого пропорційний швидкості, за даний проміжок часу зменшується в одному і тому самому відношенні;
Ø при радіоактивному розпаді маса речовини змінюється по наступному закону: за рівні проміжки часу вона змінюється в одному і тому ж відношенні;
Ø якщо колонія бактерій має достатній простір і достатню кількість поживних речовин, то її маса за рівні проміжки часу збільшується в одному і тому ж відношенні. В таких випадках говорять про процеси органічного росту.
Всі ці фізичні та біологічні процеси можна виразити через формули, які східні з формулою показникової функції.
Історична довідка: (можна в кінці уроку, якщо є час)
Термін «показник» для степеня ввів у 1553 р. німецький математик (Спочатку монах, а потім - професор) Михайль Штифель (1487-1567). По-німецьки «показник» - Exponent, з латині exponere - «виставляти на показ»; exponens, exponentis «що виставляється на показ», «той, що показується». Штифель увів дробові й нульові показники. Позначення ж ах для натуральних показників увів Рене Декарт (1637), а вільно поводитися з такими самими дробовими й від'ємними показниками почав з 1676 року Ісаак Ньютон. Степені з довільними дійсними показниками, без будь-якого загального означення, розглядали Лейбніц та Іоганн Бернуллі. 1679 р. Лейбніц увів поняття експоненціальної (тт. показникової) функції для залежності у=ахта експоненціальної кривої для графіка цієї функції. Через ехр(х) позначається конкретна експонента - з показником а=е=2,71828..., яка введена в багато мов програмування. Показникову функцію виду у=е x почали вивчати з 40-х років ХVІІ ст.
Число а=е=2,71828... позначено на честь шотландського любителя математики Джона Непера (15501617 рр.) неперовим числом.
Сьогодні на уроці навчимося будувати графік показникової функції і розглянемо її властивості.
Пояснення нового матеріалу.
Функція виду у=ах, де а>0, а≠1, називається показниковою (з основою а).
Розглянемо властивості.Показникова функція у=ах, а>0, а≠1
|
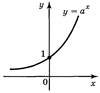
а>1 |
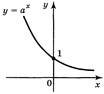
0<а<1 |
|
1. 2. Е(у): у∈(0;+ ∞ ) 3. Якщо х=0, то у=1 4. Зростає, Якщо x1>x2 тоді аx1>аx2 5. Якщо х<0, тоді у<1 6. Якщо х>0, тоді у>1 7. Найбільшого і найменшого значення нема 8. Функція ні парна, ні непарна
|
1. 2. E(y): у∈(0;+ ∞ ) 3. Якщо х=0, то у=1 4. Спадає, Якщо x1>x2 тоді аx1<аx2 5. Якщо х<0, тоді у>1 6. Якщо х>0, тоді у<1 7. Найбільшого і найменшого значення нема 8. Функція ні парна, ні непарна
|
Закріплення матеріалу
![]()
![]() Якщо основа а=0, то степінь 0х означають тільки для додатного значення аргументу х>0 і вважають, що 0х=0. Наприклад, 03 = 0, 0π = 0. Вираз 0−3 не має змісту.
Якщо основа а=0, то степінь 0х означають тільки для додатного значення аргументу х>0 і вважають, що 0х=0. Наприклад, 03 = 0, 0π = 0. Вираз 0−3 не має змісту.
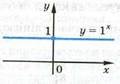
Якщо основа а<0, показник степеня х – ірраціональне число, вираз ах теж не має змісту. 1.Як ви думаєте, чому ми в означенні записали а≠1? (графіком функції у=1 x є пряма лінія паралельна вісі ОХ) Отже у=1 x не називається показниковою функцією.
2. Чи має функція розриви (ні).
3. Згадайте будь ласка, формули дій над степенями:
![]()
![]()
![]()
![]() ax ×as =ax+s (ax )s = axs acx = acxx (acb)x =axbxcx aaxs = ax :as = ax−s
ax ×as =ax+s (ax )s = axs acx = acxx (acb)x =axbxcx aaxs = ax :as = ax−s
4. Які із поданих функцій є показниковими:
|
y = 3x |
y = x3 |
y = (−2)x |
y = (0,5)x |
y =( |
3 )x |
y=6 |
y = (π)x |
5. Абітурієнтам часто на екзаменах зустрічаються і такі питання: скільки розв’язків мають рівняння типу: 2 x =0; 2 x =-3; 2 x =8. Так хто пояснить, скільки розв’язків має кожне з цих рівнянь і чому? (одне, графік неперервний)
6. Порівняйте значення виразів:
|
25 і |
23 |
2−1 і |
2−3 |
20 і |
1 |
2
2 |
4
2 |
|
35 і −19 |
0,25 і |
0,23 |
|
7. ![]()
![]() Розташуйте числа 3 2; 3
Розташуйте числа 3 2; 3![]() ; 3 10; 33; 3−1; у порядку зростання.
; 3 10; 33; 3−1; у порядку зростання.
8. Порівняйте х і у, якщо відомо, що вірна нерівність: а) 5х>5у; б) 0,1х<0,1у.
9. На рисунку зображено графіки функцій у=2х і у=3х. Чим відрізняються ці функції? Їхні графіки? (ці функції мають одинакові властивості, функція у=3х зростає більш швидше, графік цієї функції піднімається вгору більш круто).
10. Побудуйте в однієї системі координат графіки функцій f =1х y = 2x .
2 Що є спільного в графіках і чим вони відрізняються? Чи мають спільні точки?
Як розташовані графіки функцій відносно один до одного? (графіки розташовані симетрично відносно осі ОY)
|
|
|
|
Підсумки уроку. Д.з.


про публікацію авторської розробки
Додати розробку