Тема уроку.   Тематичне оцінювання № 1 “Вступ до стереометрії” та “Взаємне

                        розміщення прямих у просторі”.

Мета уроку: перевірка навчальних досягнень учнів з тем “Вступ до стереометрії” та “Взаємне розміщення прямих у просторі”.

Хід уроку

Тематичне оцінювання № 1 можна провести, враховуючи результати ви­конання самостійної роботи на уроці № 6 та результати контрольної роботи.

1. Тематична контрольна робота № 1

Варіант А

Варіант 1

1. Дано пряму а і точку А, яка не лежить на ній. Скільки можна про­вести через точку А: а) площин, які містять пряму а; б) прямих, які перетинають пряму а?  (3 бали)
2. Доведіть, що пряма с, яка перетинає дві дані паралельні прямі а і b, лежить з ними в одній площині. (3 бали)
3. Через кінець А відрізка АВ проведено площину. Через кінець В і точку С цього відрізка проведено паралельні прямі, які перетина­ють площину в точках В₁ і С₁. Знайдіть довжину відрізка СС₁, якщо ВВ₁ = a , AC : BC = т : η. (3 бали).
4. Доведіть, що діагоналі AC₁ і ΒD₁ куба ABCDA₁B₁C₁D₁ перетина­ються і точкою перетину діляться пополам. (3 бали)

Варіант 2

1. Дано пряму a і точку А на ній. Скільки можна провести через точ­ку А: а) площин, які містять пряму а; б) прямих, які паралельні прямій а? (3 бали)
2. Прямі а і b перетинаються, пряма с перетинає пряму а і паралельна прямій b. Доведіть, що прямі а, b, с лежать в одній площині. (3 бали)
3. Через кінець А відрізка АВ проведено площину. Через кінець В і точку С цього відрізка проведено паралельні прямі, які перетина­ють площину в точках B₁ і С₁. Знайдіть довжину відрізка СС₁, якщо ВВ₁ = а , АВ : АС = т : n. (3 бали)
4. В тетраедрі SABC, всі ребра якого рівні, точки Μ, Ν, К, L — сере­дини ребер AS, BS, BC, AC відповідно. Доведіть, що прямі МК і NL перетинаються під прямим кутом. (3 бали)

Варіант 3

1. Дано три точки А, В, С, які не лежать на одній прямій. Скільки можна провести: а) площин через точки А, В, С; б) прямих, які проходять через точку А і паралельні прямій BC? (3 бали)
2. Пряму а перетинають прямі b і с, причому b || с . Доведіть, що пря­мі а, b, с лежать в одній площині, (3 бали)
3. Через кінець А відрізка АВ проведено площину. Через кінець В і точку С цього відрізка проведено паралельні прямі, які перетина­ють площину в точках В₁ і С₁. Знайдіть довжину відрізка ВВ₁, якщо АВ = a, AC : CC₁ = т : n. (3 бали)
4. Точки S, А, В, С не лежать в одній площині, точки Μ, Ν, К, L — се­редини відрізків AS, BS, BC, AC відповідно. Доведіть, що відрізки МК і NL перетинаються і точкою перетину діляться пополам. (3 бали)

Варіант 4

1. Дано три точки А, В, С, які лежать на одній прямій. Скільки мож­на провести: а) площин через точки А, В, С; б) прямих через точ­ку В, які паралельні прямій АС? (3 бали)
2. Прямі а і b паралельні, пряма с перетинає пряму а, але не перети­нає пряму b. Доведіть, що прямі с і b мимобіжні. (3 бали)
3. Через кінець А відрізка АВ проведено площину. Через кінець В і точку С цього відрізка проведено паралельні прямі, які перетинають площину в точках В₁ і С₁. Знайдіть АВ, якщо ВВ₁ = а, ВС = b, СС₁ = с. (З бали)
4. Доведіть, що діагоналі АС₁, ΒD₁, СА₁, DВ₁ куба ABCDA₁B₁C₁D₁ перетинаються в одній точці. (3 бали)

Відповідь. Варіант 1. 3.. Варіант 2. 3..Варіант 3. 3.. Варіант 4. 3..

Варіант Б

Варіант 1

1. Побудуйте зображення куба ABCDA₁B₁C₁D₁. (2 бали)

Яке взаємне розміщення прямих АС та А₁C₁ ? (2 бали)

Яке взаємне розміщення прямих АВ та СВ₁ ? (2 бали)

2. Чи можна провести через точку перетину діагоналей прямокутника пряму, яка не перетинає його сторони? Відповідь обґрунтуйте. (3 бали)
3. Точки А, В, С, D не лежать в одній площині, а точки К, L, Μ, Ν — середини відрізків AD, DC, ВС, АВ відповідно. Доведіть, що прямі KM і NL перетинаються. (3 бали)

Варіант 2

1. Побудуйте зображення трикутної піраміди SABC. (2 бали)

Яке взаємне розміщення прямих AS та ВС? (2 бали)

Яке взаємне розміщення прямих AS та BS? (2 бали)

2. Чи можна через вершину трикутника провести пряму, яка не ле­жить в його площині? Відповідь обґрунтуйте. (3 бали)

3. Точки А, В, С, D не лежать в одній площині, а точки К, L, Μ, Ν — середини відрізків AD, DC, ВС, АВ відповідно. Доведіть, що точ­ка А не належить площині KLM. (З бали)

Варіант З

1. Побудуйте зображення прямокутного паралелепіпеда ABCDA₁B₁C₁D₁. (2 бали)

Яке взаємне розміщення прямих BD і АС₁ ? (2 бали)

Яке взаємне розміщення прямих BD і B₁D₁ ? (2 бали)

2. Прямі а і b перетинаються. Точки А і В належать прямій а, а точ­ка С - прямій b. Чи належать прямі α і b площині АВС? Відповідь обґрунтуйте. (З бали)

3. На трьох прямих, які лежать в площині α, взято відповідно три точки А, В, С, які належать площині β . Доведіть, що точка С ле­жить на прямій АВ. (З бали)

Варіант 4

1. Побудуйте зображення трикутника піраміди SABC. (2 бали)

Яке взаємне розміщення прямих BS та АС? (2 бали)

Яке взаємне розміщення прямих CS та СА? (2 бали)

2. Три точки А, В, С належать площині α , а точка D їй не належить. Чи може чотирикутник ABCD бути трапецією? Обґрунтуйте відпо­відь. (З бали)

3. Площини α і β перетинаються по прямій b. Пряма а лежить в площині α і перетинає площину β в точці М. Доведіть, що точ­ка Μ лежить на прямій b. (З бали).

Тематичне оцінювання № 1 можна провести за допомогою тесту, текст

якого наводиться нижче.

При оцінюванні виконання тестів враховуються тільки ті шість із ви­конаних завдань, яким відповідає найбільша кількість балів. Якщо учень набрав у сумі нецілу кількість балів, результат округляється в сторону збільшення, якщо учень набрав більше 12 балів, він одержав оцінку 12.

Тест

Аксіоми стереометрії. Взаємне розміщення двох прямих у просторі

Мета даного тесту — перевірити, чи вміє учень:

— зображати та знаходити на малюнках прямі та площини;

— застосовувати аксіоми стереометрії та наслідки з них до роз­в'язування задач;

— зображати та знаходити на малюнках паралельні, мимобіжні прямі та прямі, що перетинаються.

Варіант 1

І рівень

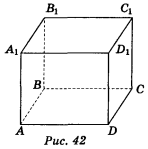
1. Дано зображення куба ABCDA₁B₁C₁D₁ (рис. 42). Які з вказаних то­чок належать площині АВС? (1 бал)

а) А₁;         б) B₁ ;         в) D;           г) D₁.

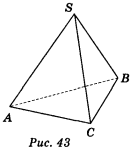
2. Дано зображення тетраедра SABC (рис. 43). Яке взаємне розміщен­ня прямих А8 і SC? (1 бал)

а) Перетинаються; б) паралельні; в) мимобіжні; г) визначити неможливо.

3. Дано зображення прямокутного паралелепіпеда ABCDA₁B₁C₁D₁ (рис. 44). Яку з вказаних площин визначають прямі АС і СС₁ ? (1 бал)

а) АВС;   б) СС₁В;  в) АСА₁;   г) BDC.

II рівень

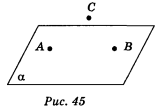
1. Точки А і В лежать у площині α , а точка С — поза нею (рис. 45). Які з наведених тверджень правильні? (1 бал)

а) Пряма АС не перетинає площину α;  б) пряма ВС не перетинає площину α;

в) прямі АВ і ВС не перетинаються;       г) прямі АВ і АС перетинаються.

2. Скільки всього різних площин можна провести через три точки, якщо вони не лежать на одній прямій? (1 бал)

а) Одну; б) дві;  в) безліч;  г) жодної.

3. Точки А, В, С, D не лежать в одній площині (рис. 46). По якій пря­мій перетинаються площини АВС і ABD ? (1 бал)

а) АВ;    б) ВС;     в) CD;     г) AD.

III рівень

1. Прямі АВ і CD не лежать в одній площині. Які з наведених твер­джень правильні? (2 бали)

а) Точки А, В, С не лежать в одній площині;

б) точки А, В, С не лежать на одній прямій;

в) точки А, В, С, D не лежать в одній площині;

г) прямі АВ і CD перетинаються.

2. Відрізки АВ, SB, SD, AC перетинають площину α. Які ще з вказа­них відрізків перетинають площину α ? (2 бали)

a) AS;   б) AD;     в) ВС;     г) SC.

3. Три прямі попарно перетинаються. Через кожні дві з них проведено площину. Скільки всього проведено площин? (2 бали)

а) Одну; б) дві;   в) три;    г) безліч.

IV рівень

1. Прямі а і b, b і с, а і с перетинаються, і точки їх перетину не збіга­ються. Які з цих тверджень правильні? (З бали)

а) Прямі а, b, с проходять через одну точку;

б) точки перетину прямих лежать на одній прямій;

в) прямі а, b, с лежать в одній площині;

г) прямі а, b, с не лежать в одній площині.

2. У просторі дано шість точок і через кожні дві з них проведено пря­мі. Яку найбільшу кількість прямих можна провести? (З бали)

а) 30;     б) 15;   в) 12;     г) 18.

3. Дано n точок у просторі (п > 4), Які з наведених тверджень пра­вильні? (З бали)

а) Завжди існує площина, в якій знаходяться всі n точок;

б) існує площина, в якій не лежить жодна з п точок;

в) завжди існує пряма, яка містить всі п точок;

г) існує пряма, яка не містить жодної з п точок.

Варіант 2

І рівень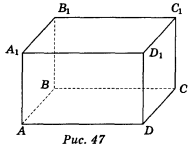             

1. Дано зображення прямокутного паралелепіпеда ABCDA₁B₁C₁D₁ (рис. 47). Які з вказаних площин проходять через пряму АВ і точку С? (1 бал)

а) АВА₁;      б) ABD;        в) ВСС₁;        г) ADD₁.

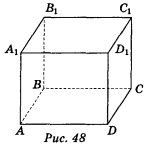
2. Дано зображення куба ABCDA₁B₁C₁D₁ (рис. 48). Яке взаємне розмі­щення прямих ВС і DD₁? (1 бал)

а) Перетинаються; б) паралельні; в) мимобіжні; г) визначити неможливо.

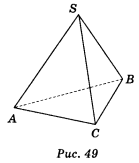
3. Дано зображення тетраедра SABC (рис. 49). Яка з вказаних точок є точкою перетину прямої SA з площиною АВС? (1 бал)

a)S;          б) В;          в)С;            г)А.

II рівень

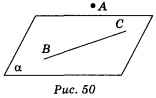
1. Пряма ВС лежить у площині α, а точка А — поза площиною α (рис. 50). Які з наведених тверджень правильні? (1 бал)

а) Пряма АВ не має спільних точок з площиною α;

б) пряма АС перетинає площину α;

в) прямі АС і ВС не перетинаються;

г) точки А, В, С не лежать у одній площині.

2. Скільки всього різних площин можна провести через пряму а і точ­ку А, яка лежить на прямій а? (1 бал)

а) Одну; б) дві;  в) безліч; г) жодної.

3. Прямі АВ і CD не лежать в одній площині. По якій прямій перети­наються площини ABD і BCD ? (1 бал)

а) АВ; б) CD:   в) BD; г) AD.

III рівень

1. Точки А, В, С, D не лежать в одній площині. Які з наведених твер­джень правильні? (2 бали)

а) Точки А, В, С не лежать в одній площині;

б) прямі АС і BD перетинаються;

в) прямі АС і BD не перетинаються;

г) точки А, В, С не лежать на одній прямій.

2. Відрізки АВ, AC, SB і BD перетинають площину α. Які ще з вказа­них відрізків перетинають площину α ? (2 бали)

а) ВС;        6) CD;         в) AD;          г) SD.

3. Скільки площин визначають чотири точки, які не лежать в одній площині?   (2 бали)

а) Дві;         б) три;         в) чотири;       г) безліч.

IV рівень

1. Прямі а і b не лежать в одній площині. Прямі с і а перетинають кожну з прямих a і b. Які з цих тверджень правильні? (З бали)

а) Прямі a і с не лежать в одній площині;

б) прямі b і с не лежать в одній площині;

в) прямі с і d лежать в одній площині;

г) прямі с і d можуть перетинатися.

2. Скільки існує площин, кожна з яких містить хоча б три вершини куба?         (З бали)

а) 6;     б) 13;   в) 20;   г) 27.

3. Дано n точок (n > 4), кожні чотири з яких лежать в одній площи­ні. Які з наведених тверджень правильні? (З бали)

а) Усі n точок лежать на одній прямій;

б) усі n точок лежать в одній площині;

в) усі n точок не лежать в одній площині;

г) усі n точок збігаються.

Відповіді до тестових завдань

II. Домашнє завдання

Якщо в класі виконувалася тематична контрольна робота № 1, то вдома можна запропонувати виконати тест, і навпаки.

III. Підведення підсумку уроку

У ході бесіди з учнями з'ясувати, які завдання викликали труднощі, та відповісти на запитання учнів.