Тематичне оцінювання "Прямі і площини в просторі"

ТА «ПРЯМІ І ПЛОЩИНИ В ПРОСТОРІ»  ВАРІАНТ 1

Заповнити пропуски в тексті:

1. Яка б не була площина, існують …, які належать цій площині, і точки, які … … їй.

2. Дві прямі в просторі називаються мимобіжними, якщо вони … … в одній площині.

3. Якщо дві паралельні площини перетинаються … …, то прямі перетину … .

4. Відстань від точки до прямої – це …

5. Прямі a та b паралельні прямій с. Яке взаємне розміщення прямих a і b?

а) перетинаються;  б) мимобіжні; в) паралельні.

6.      Скільки площин можна провести через три точки, які лежать на одній прямій?

а) одну;   б) безліч;  в) жодної.

7. Чи правильно, якщо дві прямі не мають спільної точки і не лежать в одній площині, то вони мимобіжні?

а) ні;    б) так;   в) паралельні.

8.      Скільки пар паралельних граней є у куба?

а) одна;   б) три;   в) жодної.

9.      У площині α лежить безліч прямих, паралельних площині β. Чи правильно, що α||β?

а) так;    б) ні;   в) інша відповідь.

10. Чи може трапеція бути зображенням ромба?

а) так;    б) ні;   в) інша відповідь.

11. Дано куб ABCDA₁B₁C₁D_1, яке з ребер перпендикулярне до грані AA₁B₁B?

а) С₁С;    б) CD;   в) ВС.

12. Дано куб ABCDA₁B₁C₁D₁ зі стороною 6√2 см.

  1) назвати ребра куба, мимобіжні до ребра АС;

  2) назвати ребра куба, перпендикулярні до ребра ВС;

  3) назвати площину, паралельну площині АА₁В₁В;

  4) обчислити відстань між прямими АА₁ і DD₁; 

  5) обчислити відстань між площинами АВС і А₁С₁D₁.

13. Дано зображення куба ABCDA₁B₁C₁D₁. Точка М – середина ребра АА₁. Побудувати точку перетину прямої МВ з площиною A₁B₁C_1.
14. З точки до площини проведені перпендикуляр довжиною 9см і похила довжиною 11см. Знайти довжину проекції цієї похилої на площину.
15. У трикутнику АВС кут С=90⁰, АС=9см, ВС=12см, М - середина ВА. Пряма DС перпендикулярна площині АВС, DС=18см. Знайти DМ.
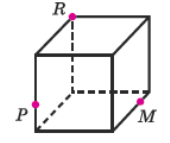
16. Побудувати переріз куба площиною, що проходить через задані точки P, R та M:

ТА «ПРЯМІ І ПЛОЩИНИ В ПРОСТОРІ»  ВАРІАНТ 2

Заповнити пропуски в тексті:

 1. Якщо дві різні прямі мають спільну …, то через них можна провести …, і до того ж тільки … .

 2. Дві прямі в просторі називаються паралельними, якщо вони … в одній площині й не … .

 3. Через точку поза площиною можна провести площину, … даній, і до того ж тільки … .

 4. Відстань між мимобіжними прямими називають …

5. Через три точки проведені дві різні площини. Як розміщені ці точки?

а) не лежать на одній прямій; б) лежать на одній прямій;  в) інша відповідь.

6.      Скільки площин можна провести через пряму і точку, що лежить на ній?

а) одну;   б) безліч;  в) жодної.

7.      Чи правильно, якщо дві прямі лежать в одній площині, то вони не мимобіжні?

а) так;    б) ні ;  в) інша відповідь.

8.      Скільки пар паралельних граней у прямокутного паралелепіпеда?

а) одна;   б) дві;   в) чотири;  г) інша відповідь.

9. Чи правильно, що дві площини, паралельні одній і тій самій прямій, паралельні між собою?

а) так;    б) ні;   в) інша відповідь.

10. Чи може прямокутник бути зображенням трапеції?

а) так;    б) ні;   в) інша відповідь.

11. Дано куб ABCDA₁B₁C₁D_1, яке з ребер перпендикулярне до грані СDD₁С₁?

а) АВ;    б) А₁А;   в) ВС.

12. Дано куб ABCDA₁B₁C₁D₁ зі стороною 3√2 см.

  1) назвати ребра куба, мимобіжні до ребра С₁С;

  2) назвати ребра куба, перпендикулярні до ребра ВС;

  3) назвати площину, паралельну площині А₁В₁С₁D₁;

  4) обчислити відстань між прямими ВВ₁ і СС₁; 

  5) обчислити відстань між площинами АА₁В₁ і D₁DC.

13. Дано зображення куба ABCDA₁B₁C₁D₁. Точка М – середина ребра АА₁. Побудувати точку перетину прямої МD з площиною A₁B₁C_1.
14. Точка віддалена від площини на 7. Знайти довжину похилої, проведеної з точки під кутом 30⁰ до площини.
15. До площини прямокутного трикутника АВС (кут С=90⁰) проведено перпендикуляр DА. Знайти відстань від точки D до точки В, якщо ВС=12 см, DС=15 см.
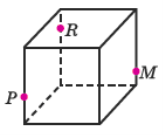
16. Побудувати переріз куба площиною, що проходить через задані точки P, R та M:

ТА «ПРЯМІ І ПЛОЩИНИ В ПРОСТОРІ»  ВАРІАНТ 3

Заповнити пропуски в тексті:

 1. Через пряму і …, яка не лежить на ній, можна провести …, і до того ж тільки … .

 2. Дві прямі, … третій … .

 3. Дві площини називаються …, якщо вони не перетинаються.

 4. Відстань між мимобіжними прямими дорівнює відстані між …

5. Прямі a, b і c попарно перетинаються. Скільки різних площин можна провести через ці прямі?

а) одну ;   б) дві;    в) три;   г) жодної.

6.      Скільки площин можна провести через три точки, які не лежать на одній прямій?

а) жодної;   б) безліч;  в) одну;  г) інша відповідь.

7.      Чи правильно, якщо дві прямі завжди лежать в одній площині?

а) так;    б) ні;   в) інша відповідь.

8. Скільки пар паралельних граней у прямій призмі, в основі якої лежить рівнобічна трапеція?

а) одна;  б) дві;   б) три;   в) чотири.

9. Чи можуть бути рівними не паралельні відрізки, які містяться між паралельними площинами?

а) так;    б) ні;   в) інша відповідь.

10. Чи може паралелограм бути зображенням прямокутника?

а) так;    б) ні;   в) інша відповідь.

11. Дано куб ABCDA₁B₁C₁D_1, яке з ребер перпендикулярне до грані АВСD?

а) A₁D₁;    б) C₁D₁;   в) C₁С.

12. Дано куб ABCDA₁B₁C₁D₁ зі стороною 4√2 см.

  1) назвати ребра куба, паралельні до ребра С₁С;

  2) назвати ребра куба, перпендикулярні до ребра AD;

  3) назвати площину, паралельну площині СС₁В₁В;

  4) обчислити відстань між прямими DD₁ і СС₁; 

  5) обчислити відстань між площинами АА₁D₁ і СС₁В₁.

13. Дано зображення куба ABCDA₁B₁C₁D₁. Точка М – середина ребра АА₁. Побудувати точку перетину прямої МВ з площиною A₁B₁C_1.
14. З точки до площини проведено перпендикуляр і похилу. Довжина похилої дорівнює 8 см, а кут між нею і перпендикуляром дорівнює 60⁰. Знайти довжини перпендикуляра та проекції похилої.
15. Через вершину С трикутника АВС до його площини проведено перпендикуляр КС. Пряма, яка проходить через точку К і середину АВ, перпендикулярна прямій АВ. Довести, що трикутник АВС – рівнобедрений.
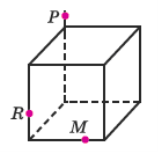
16. Побудувати переріз куба площиною, що проходить через задані точки P, R та M: