Тема уроку.  Тематичне оцінювання з теми «Перпендикулярність прямих і площин у просторі».

Мета уроку: перевірка навчальних досягнень учнів з теми «Перпендикулярність прямих і площин у просторі».

Хід уроку

Тематичне оцінювання № 4 можна провести у вигляді тематичної контрольної роботи.

1. Тематична контрольна робота № 4

Варіант А

Варіант 1

1. Побудуйте зображення куба ABCDA₁B₁C₁D₁ і запишіть грані куба, які перпендикулярні до площини А₁АС . (3 бали)
2. До площини квадрата ABCD проведено перпендикуляр SB. Знай­діть величину кута SAD. (3 бали).
3. Точка М знаходиться на однаковій відстані від всіх сторін правильно­го трикутника зі стороною 12 см і віддалена від площини трикутника на 2 см. Знайдіть відстань від точки М до сторін трикутника. (3 бали).
4. Ребро куба дорівнює а. Знайдіть відстань між діагоналлю куба і діагоналлю грані куба, яка мимобіжна з діагоналлю куба. (3 бали.)

Варіант 2

1. Побудуйте зображення куба ABCDA₁B₁C₁D₁ і запишіть грані куба, які перпендикулярні до площини B₁BD . (3 бали)
2. Дано прямокутний трикутник АВС з гіпотенузою АВ. До площини трикутника АВС проведено перпендикуляр ВМ. Знайдіть величину кута МСА. (3 бали).
3. Точка М знаходиться на відстані 2 см від кожної із сторін правиль­ного трикутника і на відстані 1 см від площини трикутника. Знай­діть сторону трикутника. (3 бали).
4. Кожне ребро трикутної піраміди дорівнює а. Знайдіть відстань між двома ребрами, які е мимобіжними (3 бали).

Варіант З

1. Побудуйте зображення куба ABCDA₁В₁C₁D₁ і запишіть грані куба, які перпендикулярні до площини АВС. (3 бали)
2. Діагоналі АС і BD ромба ABCD перетинаються в точці О. До площи­ни ромба проведено перпендикуляр AS. Знайдіть величину кута SOD. (3 бали)
3. Точка М рівновіддалена від сторін квадрата з діагоналлю 8 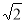см. Знайдіть цю відстань, якщо відстань від точки М до площини квад­рата дорівнює 3 см. (3 бали)
4. Знайдіть відстань між діагоналлю куба, ребро якого дорівнює а, і будь-яким ребром, мимобіжними з цією діагоналлю. (3 бали)

Варіант 4

1. Побудуйте зображення куба ABCDA₁B₁C₁D₁ і запишіть грані куба, які перпендикулярні до площини АВС₁ . (3 бали).
2. Дано рівнобедрений трикутник АВС, АВ = AC , AD — медіана три­кутника АВС. До площини трикутника проведено перпендику­ляр AS, Знайдіть величину кута SDB. (3 бали)
3. Точка М знаходиться на відстані 13 см від сторін квадрата і на відстані 12 см від площини квадрата. Знайдіть сторону квадрата. (3 бали)
4. У прямокутному паралелепіпеді ABCDA₁B₁C₁D₁ АВ = а, АА₁ = с. Знайдіть відстань між прямими АВ₁ і ВС. (3 бали)

Відповідь.  Варіант 1.1.ABCD і А₁B₁С₁D₁. 2. <SAD=90°. 3. 4 см. 4. .

Варіант 2. 1. ABCD і А₁B₁С₁D₁. 2. <MCA = 90° . 3. 6см. 4.

Варіант 3.1. ABB₁A₁, BCC₁B₁, DCC₁D₁ і ADD₁A₁. 2. <SOD = 90° . 3. 5 см. 4. .

Варіант 4. 1. ADD₁A₁ і ВСС₁В₁. 2. <SDB = 90° . 3. 10 см. 4. .

Варіант Б

Варіант 1

1. Із центра О кола, вписаного в правильний трикутник, проведено перпендикуляр SO до площини трикутника. Коло дотикається до сторони АВ у точці D, а до сторони ВС — в точці К.

а) Чому дорівнює кут між прямими OD і АВ? (2 бали)

б) Чому дорівнює кут між прямими DS і АВ? (2 бали)

в) Знайдіть відстань від точки S до сторони ВС, якщо OS = 1 cm, OK = cm. (2 бали).

2. Точка S віддалена від сторін ромба зі стороною 4 см і гострим ку­том 60° на 5 см. Знайдіть відстань від точки S до площини ромба. (3 бали)
3. Доведіть, що якщо площини α, β і γ попарно перпендикулярні, то лінії їх перетину також попарно перпендикулярні. (3 бали)

Варіант 2

1. Із центра О кола, вписаного в квадрат ABCD, проведено перпендику­ляр SO до площини квадрата. Коло дотикається до сторони ВС у точці К.

а) Яка величина кута ОКВ? (2 бали)

б) Чому дорівнює кут між прямими SK і ВС? (2 бали)

в) Знайдіть радіус вписаного кола, якщо відстань від точки S до сторони ВС дорівнює 13 см, а відстань від точки S до площини ква­драта — 5 см. (2 бали).

2. Точка S віддалена від площини трикутника АВС на 3 см і рівновіддалена від його сторін, які дорівнюють 13, 14 і 15 см. Знайдіть від­стань від точки S до сторін трикутника. (3 бали)
3. Доведіть, що якщо прямі перетину площин α, β і γ попарно пер­пендикулярні, то і площини попарно перпендикулярні. (3 бали)

Варіант З

1. Із центра О кола, вписаного в ромб ABCD, проведено перпендику­ляр SO до площини ромба. Коло дотикається до сторони АВ ромба в точці К, кут DАВ — тупий.

а) Чому дорівнює кут між прямими ОК і АВ? (2 бали)

б) Яка величина кута SKA? (2 бали)

в) Знайдіть відстань від точки S до площини ромба, якщо відстань від точки S сторони АВ дорівнює 5 см, ОК = 3 см. (2 бали).

2. Точка S рівновіддалена від сторін прямокутного трикутника, катет і гіпотенуза якого відповідно дорівнюють 4 і 5 см, і віддалена від його площини на 11 см. Знайдіть відстань від точки S до сторін трикутника. (3 бали)
3. Відомо, що площини α і β перпендикулярні. Через точку А пло­щини α проведено пряму, яка перпендикулярна до площини β. Доведіть, що ця пряма лежить у площині α. (3 бали)

Варіант 4

1. Із центра О кола, вписаного в прямокутний трикутник АВС (<C = 90°), проведено перпендикуляр SO до площини трикутника. Коло доти­кається до гіпотенузи в точці D.

а) Яка величина кута ОДА? (2 бали)

б) Яка величина кута SDB? (2 бали)

в) Знайдіть відстань від точки S до гіпотенузи трикутника АВС, якщо SO = 3 cm, OD = 4 cm. (2 бали).

2. Точка S рівновіддалена від сторін прямокутного трикутника, які дорівнюють 8, 8 і 12 см, і віддалена від його площини на 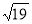см. Знайдіть відстань від точки S до сторін трикутника. (3 бали)
3. Перпендикулярні площини α і β перетинаються по прямій а. У площині α проведена пряма, перпендикулярна до прямої а. До­ведіть, що ця пряма перпендикулярна і до площиниβ. (3 бали)

Тематичне оцінювання № 4 можна провести за допомогою тесту, текст якого подано нижче.

При оцінюванні виконання тестів враховуються тільки ті шість із виконаних завдань, яким відповідає найбільша кількість балів.

Тест

Перпендикуляр і похила. Перпендикулярність площин

Мета даного тесту — перевірити, чи вміє учень:

— зображати та знаходити на малюнку перпендикуляр і похилу; перпендикулярні площини;

— розв'язувати задачі, використовувати теорему про три перпенди­куляри та ознаку перпендикулярності площин;

— визначати відстань від точки до площини; від точки до прямої тощо.

Варіант 1

І рівень

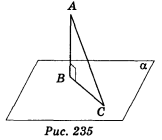
1. До площини а проведено перпендикуляр АВ і похилу АС (рис. 235). Знайти довжи­ну проекції похилої, якщо АС = 10 см, АВ = 8 см. (1 бал)

а) 8 см; б) 10 см;  в) 6 см; г) 2 см.

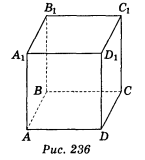
2. Знайдіть відстань від вершини А, куба ABCDA₁B₁C₁D₁ до площини ВСС₁, якщо ребро куба дорівнює 5 см (рис. 236). (1 бал)

а) 5 см;    б) 10 см;     в) 5 см;    г) визначити неможливо.

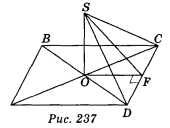
3. Через точку перетину діагоналей квадрата ABCD проведено перпен­дикуляр SO до площини квадрата і OF CD (рис. 237). Яка з вка­заних прямих перпендикулярна до прямої СD? (1 бал)

a) SC;   б) SD;  в) BD; г) SF.

II рівень

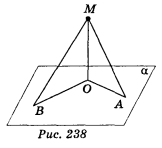
1. З точки М до площини α проведені перпендикуляр МО і похилі МА і MB (рис. 238). МО = 5 см, МА = см, MB = 13 см. (1 бал) Знайдіть відношення проекцій похилих.

а) 1:1; б)1:2; в) 1:3; г) :13.

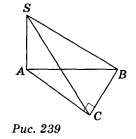
2. З вершини А прямокутного рівнобедреного трикутника АВС (<C = 90°) проведено перпендикуляр SA до площини трикутника АВС (рис. 239). AC = см, SA = см. Знайдіть площу трикутника SBC. (1 бал)

а) 1 см²;    б) см²;    в) 2 см²;     г) 2 см².

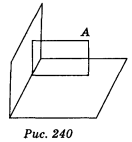
3. Точка А знаходиться на відстані 6 і 8 см від двох перпендикулярних площин (рис. 240). Знайдіть відстань від цієї точки до лінії пе­ретину площин. (1 бал)

а) 6 см;   б) 8 см;    в) 10 см;   г) 14 см.

ІІІ рівень

1. Точка S віддалена від вершин квадрата зі стороною см на 2 см. Чому дорівнює відстань від точки S до площини квадрата? (2 бали)

а) 1 см;        б) см;      в) см;       г) см.

2. Точка S віддалена від усіх сторін правильного трикутника на см, а від площини трикутника — на 3 см. Чому дорівнює сторона три­кутника? (2 бали)

а) см;     б) 3 см;        в) см;       г) 6 см.

3. Точка М рівновіддалена від сторін ромба ABCD. Які з наведених тверджень правильні? (2 бали)

а) Площина АМС перпендикулярна до площини BMD;

б) площина AМC перпендикулярна до площини АВС;

в) площина АВМ перпендикулярна до площини ADC;

г) площина BMD перпендикулярна до площини АВС:

IV рівень

1. Кожне ребро тетраедра дорівнює а. Знайдіть відстань від його вер­шини до протилежної грані. (3 бали)

a) a;       б) а;       в) а;       г) а.

2. Знайдіть відстань між мимобіжними діагоналями двох сусідніх гра­ней куба, ребро якого дорівнює а. (3 бали)

а) а;         б) а;         в) ;           г) .

3. Які з вказаних фігур можна одержати як ортогональну проекцію тетраедра, кожне ребро якого дорівнює а? (3 бали)

а) Квадрат;  б) трапецію;  в) трикутник; г) правильний шестикутник.

Варіант 2

І рівень

1. До площини а проведено перпендикуляр АВ і похилу АС (рис. 241). Знайдіть довжину похилої, якщо АВ = см, ВС = 1 см. (1 бал)

а) см;      б) 1 см;         в) 2 см;          г) 3 см.

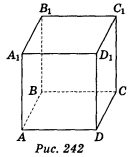
2. Знайдіть відстань від вершини А, куба ABCDA₁В₁C₁D₁ до прямої АС, якщо ребро куба дорівнює 2 см (рис. 242). (1 бал)

а) 1 см; б) 2 см;    в) 3 см;    г) визначити неможливо.

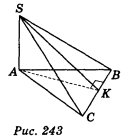
3. До площини правильного трикутника АВС проведено перпендику­ляр SA, АК ВС (рис. 243). Яка з вказаних прямих перпендикулярна до прямої ВС? (1 бал)

a) SC; б) SB; в) АВ; г) SK.

II рівень

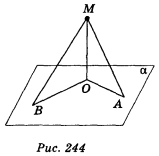
1. З точки М до площини а проведені перпендикуляр МО і похилі МА і MB (рис. 244), МО = 1 см, ОА = см, ВО = 2 см.  Знайдіть відношення довжин похилих. (1 бал)

а) 3 : 8;        б) 2 : 3;        в) : ;      г) 1 : 1.

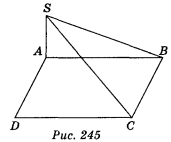
2. З вершини А квадрата ABCD проведено перпендикуляр SA до площи­ни АВС (рис. 245), AS = cm, SB = 2 см. Знайдіть площу трикут­ника SBC. (1 бал)

а) 1 см²;        б) см²;  в) 2 см²;        г) 2 см².

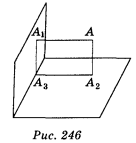
3. Точка А знаходиться на однаковій відстані від двох перпендикуляр­них площин і на відстані 2 см до лінії перетину площин (рис. 246). Знайдіть відстань від точки А до даних площин. (1 бал)

а) 1 см;   б) см;   в) 2 см;   г) визначити неможливо.

III рівень

1. Точка S віддалена від вершин правильного трикутника зі стороною см на відстань см. Чому дорівнює відстань від точки S до площини трикутника? (2 бали)

а) 1 см;        б) см;      в) 2 см;          г) см.

2. Точка S віддалена від усіх сторін правильного чотирикутника на см, а від площини чотирикутника — на 2 см. Чому дорівнює периметр чотирикутника? (2 бали)

а) 1 см;    б) 2 см; в) 4 см;     г) 8 см.

3. Точка М рівновіддалена від вершин прямокутного рівнобедреного трикутника АВС (АВ = АС), К — середина ВС. Які з наведених тверджень правильні? (2 бали)

а) Площина АМК перпендикулярна до площини АВС;

б) площина ВМС перпендикулярна до площини АВМ;

в) площина ВМС перпендикулярна до площини АВС;

г) площина АВМ перпендикулярна до площини АСМ.

IV рівень

1. Три ребра тетраедра SA, SB, SC взаємно перпендикулярні і дорівню­ють а. Знайдіть відстань від вершини S до площини АВС. (3 бали)

а) а;            б) ;        в) ;          г) .

2. Знайдіть відстань між діагоналлю куба і мимобіжною з нею діаго­наллю грані куба, якщо ребро куба дорівнює а. (3 бали)

а) ;            б) ;        в) ;          г) .

3. Які з вказаних фігур можна одержати як ортогональну проекцію куба? (3 бали)

а) Квадрат;    б) прямокутник, відмінний від квадрата;

в) п'ятикутник;      г) шестикутник.

Відповіді до тестових завдань

II. Домашнє завдання

Якщо в класі виконувалася тематична контрольна робота № 4, то вдома можна запропонувати виконати тест, і навпаки.

III. Підведення підсумку уроку

У ході фронтальної бесіди з'ясувати, які завдання викликали труд­нощі, та відповісти на запитання учнів.