Тема уроку. Відстань між двома точками простору.

Мета уроку: виведення формул для знаходження відстані між двома точками, заданих координатами, та застосування формули до розв'язування задач.

Обладнання: схема «Відстань між двома точками», модель куба.

Хід уроку

І. Перевірка домашнього завдання

1. Усне коментування розв'язування домашніх завдань.

2. Математичний диктант.

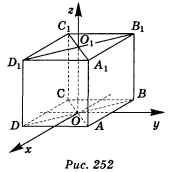
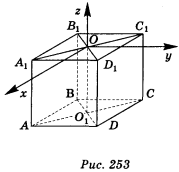
Ребро куба дорівнює 10: варіант 1 — рис. 252, варіант 2 — рис. 253. Запишіть координати точок: А, В, С, D, О, О₁, А₁, В₁, С₁, D₁.

Відповідь.

Варіант 1. А(5; 5; 0), В(-5; 5; 0), С(-5;-5; 0), D(5; -5; 0), O(0; 0; 0), 0₁(0; 0; 10), А₁(5; 5; 10), B₁ (-5; 5; 10), С₁(-5; -5; 10), D₁(5; -5; 10).

Варіант 2. А(5; -5; -10), В(-5; -5; -10), C(-5; 5; -10),   D(5; 5; -10), O(0; 0; 0), O₁(0; 0; -10), A₁(5; -5; 0), B₁(-5; -5; 0), C₁(-5; 5; 0), D₁(5; 5; 0).

II. Актуалізація опорних знань

Розв'язування задач

1. Знайдіть відстань між двома точками, які лежать на координатній прямій:

a) A(l) і В(5);     б) А(-5) і В(-7);  в) А(-3) і В(5);    г) А(а) і В(b) .

2. Знайдіть відстань між двома точками, які лежать на координатній площині:

а) А (1:2) і В (4; 6);        б) A(1; 7) i В (-5;-1);  в) А(х_A; y_A)і В(х_B; у_B).

III. Сприйняття й усвідомлення нового матеріалу

Твердження.

Квадрат, відстані між двома точками дорівнює сумі квад­ратів різниць їх відповідних координат.

Доведення

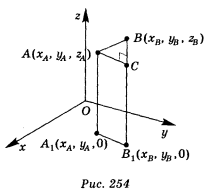
Нехай дано дві точки А(x_A, у_A, z_A) і В(х_B, y_B, z_B) (рис. 254). Доведе­мо, що

АВ² = (х_B – x_A)² + (y_B – у_A)² + (z_B – z_A)². 

Розглянемо випадок, коли АВ не паралельна осі z. Через точки А і В проведемо прямі, паралельні осі z. Вони перетнуть площину ху в точках A₁ і В₁ відповідно. Ці точки мають ті самі координати х, у, що й точки А і В, а координата z їх однакова і дорівнює нулю. Проведемо через точку А площину, паралель­ну координатній площині ху. Побудована площина перетне пряму ВВ₁ у деякій точці С, причому ВС = | z_B – z_A|. За теоремою Піфагора із ΔАВС маємо:

АВ² = AC² + ВС². Оскільки АС² = A₁В₁² = (х_B – x_A)² + (y_B – у_A)² ,

ВС = | z_B – z_A |, то АВ² = (х_B – x_A)² + (y_B – у_A)² + (z_B – z_A)².

Таким чином, відстань між точками А(x_A, у_A, z_A) і В(х_B, y_B, z_B) обчислюється за формулою .

Розв'язування задач

1. Знайдіть відстань АВ, якщо А(-1; 3; -1), В(-1; 0; - 5). (Відповідь. АВ = 5.)

2. Знайдіть відстань від точки А(-1; 2; - 2) до початку координат.

(Відповідь. ОА = 3.)

3. Знайдіть периметр трикутника АВС, якщо А (7; 1; -5), В (4;-3;-4), C (1;3;-2). (Відповідь. 14 + .)

4. Чи лежать точки А, В, С на одній прямій, якщо А(3;2;2), В(1;1;1), С(-1;0;0)? (Відповідь. Так.)

5. На якій відстані від координатних площин і координатних осей розташована точка А (- 2; 3; 4) ?

(Відповідь. АА_x = 5; АА_y = 2; АА_z = ; АА_xy = 4 ; АА_xz = 3; АА_yz = 2.)

6. Яка з точок — А (2; 1; 6) чи В (-2; 1; 6) — лежить ближче до почат­ку координат? (Відповідь. Точка А.)

7. Дано точки К(0; 2; 1), Р(2; 0; 3) і T(-1; у; 0). Знайдіть таке зна­чення у, щоб виконувалась умова: КТ = РТ . (Відповідь. -3.)

8. Задача № 5 із підручника (с. 55).

9. Задача № 8 із підручника (с. 55).

III. Домашнє завдання

§ 4, п. 24; контрольне запитання № 2; задачі № 4, 6, 7 (с. 55).

IV. Підведення підсумку уроку

При підведенні підсумку уроку можна скористатися наведеною схемою.

Запитання до класу

1) Як знайти відстань між двома точками на координатній прямій?

2) Як знайти відстань між двома точками координатної площини?

3) Як знайти відстань між двома точками простору?