Тематичні контрольні роботи з геометрії 8 клас

 

 

О. Я. Федак

 

 

 

 

 

 

 

 

 

 

 

 

 

У методичних рекомендаціях вміщені тематичні контрольні роботи з усіх тем курсу геометрії 8клас відповідно до вимог програми.

 

 

Матеріали зібрала і упорядкувала вчитель математики Федак О.Я.

 

 

                            

Передмова

 

       Методичні рекомендації тематичних контрольних робіт для 8-го класу складені з усіх тем курсу геометрії 8 класу  відповідно до вимог програми.

       Запропоновані контрольні роботи повністю відповідають діючій програмі з геометрії у 8-му класі.

       Робота з кожної теми містить 2 варіанти, а кожний варіант містить завдання чотири рівні складності. Кожен рівень оцінюється трьома балами.

        Рівень І (початковий) представлений у вигляді тестів, які включають усі основні поняття даної теми.

        Рівень ІІ (середній) містить завдання з одно-два кроковими завданнями. Виконання цих завдань дозволить учням продемонструвати рівень обов’язкових знань, набутих учнями у процесі навчання.

         Рівень ІІІ (достатній) містить завдання, виконання яких виявить в учнів уміння й навички самостійного розв’язування стандартних задач.

           Рівень ІV ( високий) містить завдання підвищеної складності, розв’язання яких передбачає використання набутих знань і вмінь у нестандартних ситуаціях.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тематична контрольна робота № 1          

Тема: Чотирикутники. Паралелограм, прямокутник, ромб, квадрат.

Варіант І

 

І рівень

 

1. У чотирикутнику АВСD АС – його діагональ,                кут ВСА = 20^о, а протилежні сторони  ВС і АD паралельні. Чому дорівнює кут САD?

           А) 160^о,  Б) 20^о,  В) 40^о,  Г) 80^о.

2. Закінчити речення :

 Ромб – це ………………………………….

3. Скільки треба знати сторін паралелограма, щоб знайти його периметр?

 

ІІ рівень

 

4. Одна з діагоналей ромба дорівнює його стороні. Чому дорівнюють кути ромба?
5. Периметр паралелограма дорівнює 46 см. Знайдіть довжини його сторін, якщо одна сторона на 3 см більша від другої.                                                                                   

 

ІІІ рівень

 

6. У паралелограмі бісектриса кута ділить протилежну сторону на відрізки, які дорівнюють 25 см і 15 см. Знайдіть периметр паралелограма.

 

ІV рівень

 

7. Діагональ прямокутника ділить кут на два кути які відносяться як 2:3. Знайдіть кут, який утворюють між собою діагоналі прямокутника.

 

 

 

 

Тематична контрольна робота № 1          

Тема: Чотирикутники. Паралелограм, прямокутник, ромб, квадрат.

Варіант ІІ

 

І рівень

 

1.У паралелограмі АВСD діагоналі перетинаються в точці О. Чим для трикутника АСD є відрізок ОD?

А) Висотою,   Б) бісектрисою,  В) медіаною.

1. Закінчити речення :

 Квадрат  – це ………………………………….

2. Скільки треба знати сторін ромба, щоб знайти його периметр?

 

ІІ рівень

 

3. У ромбі АВСD кут D = 120^о. Знайдіть кути трикутника АОD. (О – точка перетину діагоналей).                                                                                                               
4. Периметр паралелограма дорівнює 36 см. Знайдіть довжини його сторін, знаючи, що діагональ паралелограма ділить його кут на два кути 90^о і 30^о.

 

ІІІ рівень

 

6. Менша діагональ ромба дорівнює 12 см, а гострий кут його дорівнює 60^о. Знайдіть периметр ромба.                                                                                                                 

ІV рівень

 

8. Діагоналі прямокутника утворюють між собою кут 72^о. Як відносяться  кути, на які поділила кут прямокутника його діагональ?

 

 

 

 

 

Тематична контрольна робота № 2          

Тема:  Теорема Фалеса. Трапеція. Середня лінія трикутника, трапеції.

 

Варіант 1

І рівень.

У завданнях 1 – 3 виберіть і підкресліть правильну відповідь.

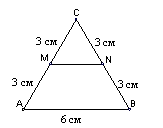
1.   На рисунку AM = MC = 3 см, BN = NC = 3 см, AB = 6 см.

Довжина відрізка MN дорівнює:

а) 3 см;

б) 4 см;

в) 5 см.

2.   У трапеції ABCD величина кута DAB дорівнює 45° (див. рисунок).

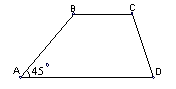Величина кута ABC дорівнює:

а) 45°;

б) 90°;

в) 135°.

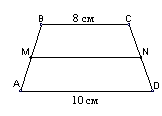3.   Відрізок MN у трапеції ABCD є середньою лінією (див. рисунок).

Якщо AD = 10 см, BC = 8 см, то MN дорівнює:

а) 18 см;

б) 12 см;

в) 9 см.

 

ІІ рівень.

4.   У трапеції ABCD кути, прилеглі до основи AD, дорівнюють 150° і 70°. Знайдіть кути, прилеглі до основи BC.

5.   Розділіть даний відрізок на три рівні частини за допомогою циркуля і лінійки.

 

ІІІ рівень.

 

6. По один бік від прямої дано дві точки А і В на відстані 6 см і 14 см від неї. Знайдіть відстань від середини відрізка АВ до прямої.

 

IV рівень.

7.   Знайдіть периметр рівнобічної трапеції, якщо її гострий кут дорівнює 60°, а довжини основ дорівнюють 8 см і 4 см.

 

 

 

 

Тематична контрольна робота № 2          

Тема:  Теорема Фалеса. Трапеція. Середня лінія трикутника, трапеції.

Варіант 2

І рівень.

У завданнях 1 – 3 виберіть і підкресліть правильну відповідь.

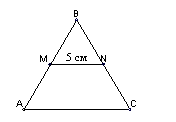1.   На рисунку MN – середня лінія трикутника ABC, MN = 5 см.

Довжина сторони АС дорівнює:

а) 6 см;

б) 8 см;

в) 10 см.

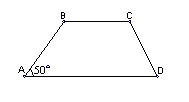2.   У рівнобічній трапеції ABCD (BC  AD) величина кута BAD дорівнює 50° (див. рисунок).

Тоді величина кута CDA дорівнює:

а) 40°;

б) 50°;

в) 60°.

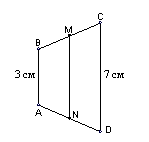3.   Відрізок MN – середня лінія трапеції ABCD (AB  CD) (див. рисунок). Якщо AB = 3 см,

CD = 7 см, то довжина відрізка MN дорівнює:

а) 4 см;

б) 5 см;

в) 6 см.

 

ІІ рівень.

4.   У трапеції ABCD кути, прилеглі до основи BC, дорівнюють 100° і 90°.

Знайдіть кути, прилеглі до основи AD.          

5.   Розділіть даний відрізок на п’ять рівних частин за допомогою циркуля і лінійки.

                 

          

ІІІ рівень.

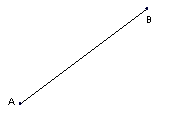
7.   Кінці діаметра віддалені від дотичної до кола на 5 см і 15 см. Знайдіть радіус кола.          

          

IV рівень

8.   Знайдіть периметр рівнобічної трапеції, якщо тупий кут дорівнює 120°, а довжини основ дорівнюють 6 см і 2 см.

 

Тематична контрольна робота № 3

        

Тема:  Подібність трикутників.

Узагальнена теорема Фалеса. Ознаки подібності  трикутників.

 

Варіант 1

 

І рівень

 

1.  АВС подібний  А1В1С1. Записати рівні кути трикутників.
2.   АВС подібний  А1В1С1. Знайти невідомі кути трикутників, якщо кут В= 40^о  , кут А1 = 70^о 
3.  АВС подібний  А1В1С1 . Знайти коефіцієнт подібності трикутників, якщо АВ=10см і А₁В₁=20см.

 

 

ІІ рівень

 

4. Чи подібні трикутники АВС і АКР, якщо КР – середня  лінія трикутника АВС. Обгрунтувати.
5. АВС подібний АВС . Знайти А₁В₁ і В₁С₁, якщо АВ=5см, ВС=7см, АС=14см, А₁С₁=28см.

 

 

ІІІ рівень

 

6. Два кути одного трикутника відповідно дорівнюють двом кутам другого. Сторони першого трикутника відносяться як 4:5:6. Знайти сторони другого трикутника, якщо його периметр дорівнює 45см.

 

 

IV рівень

 

7. У трикутнику з усіх вершин проведено висоти. Довести, що трикутники, які мають спільну вершину з даним трикутником, подібні між собою.

 

 

 

Тематична контрольна робота № 3

        

Тема:  Подібність трикутників.

Узагальнена теорема Фалеса. Ознаки подібності  трикутників.

 

Варіант 2

 

І рівень

 

1. АВС подібний  А1В1С1. Записати рівні кути трикутників.

2.   АВС подібний     А1В1С1. Знайти невідомі кути трикутників, якщо кут В= 55^о  , кут А1 = 75^о 

3. АВС подібний   А1В1С1 . Знайти коефіцієнт подібності трикутників, якщо АВ=12см і А₁В₁=24см.

 

 

ІІ рівень

 

4.Чи подібні трикутники АВС і ВМК, якщо МК – середня  лінія трикутника АВС. Обгрунтувати.

5.АВС подібний АВС . Знайти А₁В₁ і В₁С₁, якщо АВ=7см, ВС=9см, АС=12см, А₁С₁=24см.

 

 

ІІІ рівень

 

8. Два кути одного трикутника відповідно дорівнюють двом кутам другого. Сторони першого трикутника відносяться як 2:5:4. Знайти сторони другого трикутника, якшо його периметр дорівнює 55см.

 

 

IV рівень

 

9. У трикутнику АВС з гострим кутом С проведено висоти АМ і ВР. Довести, що трикутники АВС і  МРС подібні між собою.

 

 

Тематична контрольна робота № 4

        

Тема:  Многокутники. Площі многокутників.

 

Варіант 1

 

І рівень

1. Обчислити площу прямокутного трикутника з катетами 10см і 4,5см.

а) 45см;

б) 450см;

в)22,5см.

2. Знайти площу прямокутника зображеного на малюнку.

а

в

а) ав+в²;                 В         С                    

б) а+в  в;                                                                                 в                                                

в) а²+в².                 А                                                        D  

3. Діагоналі ромба дорівнюють 16см і 20см. Знайти площу ромба.

     

  ІІ рівень

 

4. Обчислити площу квадрата, діагональ якого дорівнює 20см.

а) 400см² ;

б) 200см² ;

в) 100см².

5. Менша основа рівнобічної трапеції дорівнює 4см, а її висота – 5см.

   Обчислити площу трапеції, якщо гострий кут дорівнює 45^о

 

ІІІ рівень

 

6. Основи трапеції 10см і 8см, а діагоналі – 9см і 12см. Обчислити площу трапеції.

 

IV рівень

 

7. Доведіть, що бісектриси двох протилежних кутів паралелограма паралельні.

                                          

 

 

 

Тематична контрольна робота № 4

        

Тема:  Многокутники. Площі многокутників.

 

Варіант 2

 

І рівень

1. Сторони паралелограма дорівнюють 10см і 8см, а кут між ними 30^о. Знайти площу паралелограма.

а) 80см²;

б) 40см²;

в) 36см².

2. Знайти площу прямокутника зображеного на малюнку.

а

в

а) ав+а²;                                              

б) а²+ав;                                                                                 а                                                

в) а+в  а.                                                                         

 

3. Діагоналі ромба дорівнюють 14см і 10см. Знайти площу ромба.

     

  ІІ рівень

 

4. Обчислити площу квадрата, діагональ якого дорівнює 12см.

а) 72см² ;

б) 120см² ;

в) 144см².

5. Більша  сторона паралелограма дорівнює 10см, а його висоти 3см і 5см. Знайти меншу сторону паралелограма.

 

ІІІ рівень

 

6. Основи трапеції 60см і 20см, а бічні сторони 13см і 37см. Обчислити площу трапеції.

 

IV рівень

 

7. Доведіть, що бісектриси двох  кутів, прилеглих до однієї сторони паралелограма, взаємно перпендикулярні.

                                          

Тематична контрольна робота № 5

        

Тема:  Розв’язування прямокутних трикутників.

 

Варіант 1

 

 І рівень

 

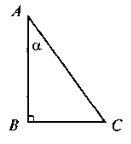
1. На рисунку в прямокутному трикутнику ABC B = 90°, A = α.

а) Виразіть cos α;

б) виразіть гіпотенузу АС через катет ВС і тригонометричну функцію кута α;

в) виразіть   sin C    через   тригонометричну функцію кута α.

 

 ІІ рівень

 

2. Спростіть вираз 3 sin² α + 3 cos² α.
3. Синус гострого кута втричі більший за його косинус. Чому дорів­нює тангенс даного кута?

 

  ІІІ рівень

 

4. Розв'яжіть прямокутний трикутник з гіпотенузою 6 см і гострим кутом 30°.
5. Знайдіть тангенс гострого кута α, якщо cos α = 0,8.

 

IV рівень

 

6. Знайдіть висоту й бічну сторону рівнобедреної трапеції з основами 2 і 8см та гострим кутом α.

 

 

 

 

 

 

 

 

 

Тематична контрольна робота № 5

        

Тема:  Розв’язування прямокутних трикутників.

 

Варіант 2

 

І рівень

 

1. На рисунку в прямокутному трикутнику ABC A = 90°, C = γ.

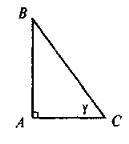а) Виразіть sin γ;

б) виразіть катет АВ через катет АС і три­гонометричну функцію кута γ;

в) виразіть   cos γ   через  тригонометричну функцію кута γ.

 

 

ІІ рівень

 

2. Спростіть вираз 2 – sin² α – cos² α.
3. Синус гострого кута вдвічі менший за його косинус. Чому дорів­нює тангенс даного кута?

 

ІІІ рівень

 

4. Розв'яжіть прямокутний трикутник із катетом 4 см і прилеглим ку­том 60°.
5. Знайдіть тангенс гострого кута α, якщо sin α = 0,6.

 

IV рівень

 

 

6. Знайдіть діагоналі ромба зі стороною 6см і гострим кутом α.

 

 

 

 

 

 

Підсумкова контрольна робота  

 

І варіант

 

І рівень

Виберіть правильний варіант відповіді:

 1. Якщо сторона квадрата дорівнює 6см, то його периметр дорівнює…

а) 12см;             б) 24см;         в) 36см;           г)18см.

2. Якщо основи трапеції дорівнюють 4см і 8см, то середня лінія трапеції дорівнює:

а) 4см;          б) 8см;        в) 6см;           г) 12см.

3. Якщо АВС подібний  А1В1С1. АВ=112см, ВС=16см, А₁В₁=6см,

   В=40^о. Знайдіть В₁  і   В₁С_1.

а) 20^о і 16см;          б) 40^о і  8см;           в) 40^о і 16см.

 

ІІ рівень

 

4. Периметр прямокутника дорівнює 100 см. Одна з його сторін на

     6 см менша, ніж інша. Визначити всі сторони  прямокутника

5. В паралелограмі АВСD висота ВК поділяє сторону АD на відрізки АК і КD. Знайти сторони паралелограма, якщо ВК=8 см, АК=15 см, ВD=10 см.

 

ІІІ рівень

 

6.  В трапеції АВСД з основами АД=22 см і ВС=16 см проведена середня лінія МN, яка перетинає діагональ АС в точці L. Чому дорівнюють відрізок ML і середня лінія МN?

 

IV рівень

 

7.  У трикутнику АВС  з вершинами в точках А(2;-3), В(-2;3) та

 С(6;-3) проведена середня лінія В₁С₁, паралельна стороні ВС. Знайти довжину В₁С₁. Скласти рівняння прямої, яка містить цю середню лінію.

 

 

 

 

Підсумкова контрольна робота  

 

 

 

ІІ варіант

 

І рівень

Виберіть правильний варіант відповіді:

 1. Один з кутів паралелограма дорівнює 45^о. Знайдіть інші кути паралелограма.

а) 45^о, 135^о, 135^о;             б) 45^о, 45^о, 135^о ;         в) 45^о, 45^о, 45^о .

2. Якщо основи трапеції дорівнюють 6см і 8см, то середня лінія трапеції дорівнює:

а) 14см;          б) 7см;        в) 6см;           г)  8см.

3. Якщо АВС подібний А1В1С1. А=60^о АВ=10см, В₁С₁=8см, А₁В₁=5см. Знайдіть А₁  і   ВС_.

а) 60^о і 16см;          б) 60^о і  8см;           в) 30^о і 16см.

 

 

ІІ рівень

 

4.   Периметр паралелограма дорівнює 98 см. Одна з його сторін на                           7см більша, ніж інша. Визначити всі сторони паралелограма.

5.  В трапеції МОРК проведені висоти ОВ і РА, які поділяють більшу основу на відрізки МВ, ВА і АК. Знайти меншу основу та бічні сторони трапеції якщо МВ=8 см, ВА=9 см, АК=12 см, АР=6 см.

 

ІІІ рівень

 

6.  Діагоналі трапеції поділяють її середню лінію на частини, кожна з яких дорівнює 7 см. Визначити основи трапеції.

 

IV рівень

 

7.  У трикутнику АВС з вершинами в точках А(-1; 2), В(5; -10) і

С(1; -2) проведена середня лінія А₁В₁, паралельна стороні АВ. Знайти довжину А₁В₁. Скласти рівняння прямої, яка містить цю середню ліні

 

 

Використана література

 

1.  А.Г. Мерзляк, В.Б. Полонський, Ю.М. Рабінович, М.С. Якір

     Геометрія.    Збірник задач і контрольних робіт для 8-го класу.

      Харків, «Гімназія» 2012р.

2. Т.Л. Корнієнко, В.І. Фіготіна       Геометрія.    Збірник задач і контрольних робіт для 8-го класу.

      Видавництво  «Ранок» 2012р.

3. Л.В. Дудко Т.Г. Роєва Геометрія.    Зошит з елементами тестування для 8-го класу.

     Харків, «Гімназія» 2012р .

4. Л.П. Карцан  Навчаючі самостійні роботи з геометрії для 8-го класу.

Харків, «Гімназія» 2012р .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ЗМІСТ

1. Передмова………………………………………………3
2.  Тематична контрольна робота №1 з теми «Чотирикутники. Паралелограм, прямокутник, ромб, квадрат»………………..4
3. Тематична контрольна робота №2 з теми «Теорема Фалеса. Трапеція. Середня лінія трикутника, трапеції»………………6
4. Тематична контрольна робота №3 з теми « Подібність трикутників» …………………………………………………...8
5.   Тематична контрольна робота №4 з теми «Многокутники. Площі многокутників»………………………………………..10
6.   Тематична контрольна робота №5 з теми «Розв’язування прямокутних трикутників»…………………………………...12
7. Підсумкова контрольна робота………………………………14

Використана література…………………………………………16